蜗杆计算公式

蜗轮蜗杆的传动比计算公式
蜗轮蜗杆传动是常见的一种传动方式，其传动比的计算公式为：传动比 = （蜗轮齿数÷蜗杆螺旋角度）×（蜗杆螺距÷蜗杆齿数）
其中，蜗轮齿数指蜗轮上的齿数，蜗杆螺旋角度指蜗杆螺旋线与蜗轮轴线之间的夹角，蜗杆螺距指蜗杆上一个螺旋线所走过的距离，蜗杆齿数指蜗杆上的齿数。

在计算传动比时，需要注意蜗轮齿数和蜗杆齿数的单位要保持一致，一般都是用个数来表示。

同时，蜗杆螺距和蜗杆齿数的单位也要一致，一般都是用长度来表示。

通过以上公式，我们可以计算出任意给定的蜗轮蜗杆传动的传动比，从而帮助我们进行传动方案的设计和选择。

- 1 -。

蜗杆计算公式全部蜗杆计算公式。

蜗杆传动是一种常见的机械传动方式，它由蜗杆和蜗轮组成，通过蜗杆的旋转来驱动蜗轮的旋转，实现传动效果。

在实际工程中，需要对蜗杆传动进行计算，以确定其传动参数和性能。

下面将介绍蜗杆传动的计算公式及其应用。

蜗杆的基本参数。

在进行蜗杆传动的计算之前，首先需要了解蜗杆的基本参数。

蜗杆的基本参数包括蜗杆的模数、节圆直径、蜗杆的导程、蜗杆的螺旋角等。

这些参数可以通过蜗杆的设计图纸或者实际测量获得。

在进行蜗杆传动的计算时，需要根据这些参数来确定传动比、效率等。

蜗杆传动的传动比计算公式。

蜗杆传动的传动比是指蜗杆旋转一圈，蜗轮旋转的圈数。

传动比的大小对于蜗杆传动的性能有着重要的影响。

传动比的计算公式如下：传动比 = 蜗轮的齿数 / 蜗杆的螺旋数。

其中，蜗轮的齿数可以通过蜗轮的设计图纸或者实际测量获得，蜗杆的螺旋数是蜗杆的基本参数之一。

通过这个公式，可以很容易地计算出蜗杆传动的传动比，从而为后续的设计和计算提供基础数据。

蜗杆传动的效率计算公式。

蜗杆传动的效率是指输入功率与输出功率之比，它是衡量蜗杆传动性能的重要指标。

蜗杆传动的效率计算公式如下：效率 = 输出功率 / 输入功率。

其中，输出功率可以通过蜗轮的扭矩和转速计算得到，输入功率可以通过输入轴的扭矩和转速计算得到。

通过这个公式，可以很容易地计算出蜗杆传动的效率，从而评估蜗杆传动的性能优劣。

蜗杆传动的扭矩计算公式。

蜗杆传动的扭矩是指蜗轮上的扭矩，它是衡量蜗杆传动输出性能的重要指标。

蜗杆传动的扭矩计算公式如下：扭矩 = 力臂力。

其中，力臂是指蜗轮上的力作用点到转轴的距离，力是指作用在蜗轮上的力。

通过这个公式，可以很容易地计算出蜗杆传动的扭矩，从而评估蜗杆传动的输出性能。

蜗杆传动的功率计算公式。

蜗杆传动的功率是指蜗轮上的功率，它是衡量蜗杆传动输出性能的重要指标。

蜗杆传动的功率计算公式如下：功率 = 扭矩转速。

其中，扭矩是指蜗轮上的扭矩，转速是指蜗轮的转速。

蜗轮的计算公式：1传动比=蜗轮齿数×蜗杆头数2中心距=（蜗轮节圆直径+蜗轮节圆直径）△2三。

蜗轮中径=（齿数+2）×模数4蜗轮齿数×蜗轮模数5蜗杆螺距直径=蜗杆外径-2×模数6蜗杆引线=π×元件×头数7螺旋角（前角）TGB=（模数×头数）×蜗杆节径基本参数：蜗轮蜗杆模数m、压力角、蜗杆直径系数Q、导程角、蜗杆头数、蜗杆齿数、齿高系数（1）、间隙系数（0.2）。

其中，模数m和压力角是蜗轮轴表面的模数和压力角，即蜗轮端面的模数和压力角，两者均为标准值。

蜗杆直径系数q是蜗杆分度圆直径与其模数M的比值。

蜗轮蜗杆正确啮合的条件：在中间平面，蜗杆和蜗轮的模数和压力角分别相等，即蜗轮端面的模数等于蜗杆轴线的模数，即标准值。

蜗轮端面的压力角应等于蜗杆的轴向压力角和标准值，即==M。

当蜗轮的交角一定时，必须保证蜗轮和蜗杆的螺旋方向一致。

蜗轮结构通常用于在两个交错轴之间传递运动和动力。

蜗轮相当于中间平面上的齿轮和齿条，蜗杆和螺钉的形状相似。

分类这些系列大致包括：1。

Wh系列蜗轮减速器：wht/whx/whs/whc2；CW系列蜗轮减速器：CWU/CWS/cwo3；WP系列蜗轮减速器：WPA/WPS/WPW/WPE/wpz/wpd4；TP系列包络蜗轮减速器：TPU/TPS/TPA/tpg5；PW型平面双包环面环面蜗杆减速器；另外，根据蜗杆的形状，蜗杆传动可分为圆柱蜗杆传动、环形蜗杆传动和斜蜗杆传动。

[1]组织特征1该机构比交错斜齿轮机构具有更大的传动比。

2两轮啮合齿面间存在线接触，其承载能力远高于交错斜齿轮机构。

三。

蜗杆传动相当于螺旋传动，即多齿啮合传动，传动平稳，噪音低。

4当蜗杆的导程角小于啮合齿间的等效摩擦角时，该机构具有自锁性能，可以实现反向自锁，即只有蜗杆可以驱动蜗轮，而不能驱动蜗轮。

起重机械采用自锁蜗杆机构，其反向自锁性能能起到安全防护作用。

蜗杆蜗轮分度圆计算公式蜗杆蜗轮传动是一种常见的传动形式，它具有传动比大、传动平稳、噪音小等优点，在工业生产中得到了广泛的应用。

蜗杆蜗轮的设计与计算是蜗杆蜗轮传动的关键，其中蜗杆蜗轮的分度圆计算是设计中的重要环节。

本文将介绍蜗杆蜗轮分度圆的计算公式及其相关知识。

蜗杆蜗轮的分度圆是指蜗轮上的分度圆，它决定了蜗轮的齿数、齿廓等重要参数。

蜗杆蜗轮的分度圆计算公式主要包括蜗杆分度圆的计算和蜗轮分度圆的计算两部分。

首先是蜗杆分度圆的计算。

蜗杆的分度圆直径可以通过以下公式计算：d = m z。

其中，d为蜗杆分度圆直径，m为模数，z为蜗杆的齿数。

模数是蜗杆蜗轮传动中的重要参数，它是齿轮的模型参数，表示齿轮齿数与分度圆直径的比值。

通过选择合适的模数，可以满足传动的强度、精度和传动比等要求。

接下来是蜗轮分度圆的计算。

蜗轮的分度圆直径可以通过以下公式计算：D = m z。

其中，D为蜗轮分度圆直径，m为模数，z为蜗轮的齿数。

与蜗杆分度圆类似，蜗轮的分度圆直径也是通过模数和齿数来计算的。

在实际设计中，需要根据传动比、工作条件等因素来选择合适的模数和齿数，以满足设计要求。

除了分度圆直径的计算公式外，还需要考虑蜗杆蜗轮的齿廓参数。

蜗杆蜗轮的齿廓是蜗杆蜗轮传动中的重要参数，它直接影响着传动的效率和精度。

在实际设计中，需要根据蜗杆蜗轮的齿廓参数来确定蜗杆和蜗轮的齿形，以保证传动的平稳性和精度。

总之，蜗杆蜗轮的分度圆计算是蜗杆蜗轮传动设计中的重要环节，它直接影响着传动的性能和可靠性。

通过合理的计算公式和参数选择，可以设计出性能优良的蜗杆蜗轮传动装置，满足工程应用的要求。

希望本文介绍的蜗杆蜗轮分度圆计算公式及相关知识能够对蜗杆蜗轮传动的设计和应用有所帮助。

1模数蜗杆的螺距
模数蜗杆的螺距指的是蜗杆上相邻两个蜗杆螺旋线之间的距离。

螺距是蜗杆的一个重要参数，通常用来描述蜗杆的线速度和传动比。

螺距的单位是长度，比如毫米或英寸。

螺距与蜗杆的直径和蜗杆的蜗杆角有关。

螺距的计算公式如下：
螺距 = 3.14 * 蜗杆直径 / tan(蜗杆角)
其中，蜗杆直径是指蜗杆最大直径，也可以取蜗杆径向20%位置处的直径进行计算。

蜗杆角是蜗杆螺旋线与轴线的夹角。

需要注意的是，螺距是一个设计参数，在实际制造过程中会根据需求和机械结构进行调整。

螺距的选择会影响蜗杆的负载能力、传动效率等性能指标。

模数蜗杆的螺距指的是蜗杆上相邻两个蜗杆螺旋线之间的距离。

螺距是蜗杆的一个重要参数，通常用来描述蜗杆的线速度和传动比。

螺距的单位是长度，比如毫米或英寸。

螺距与蜗杆的直径和蜗杆的蜗杆角有关。

螺距的计算公式如下：
螺距 = 3.14 * 蜗杆直径 / tan(蜗杆角)
其中，蜗杆直径是指蜗杆最大直径，也可以取蜗杆径向20%位置处的直径进行计算。

蜗杆角是蜗杆螺旋线与轴线的夹角。

需要注意的是，螺距是一个设计参数，在实际制造过程中会根据需求和机械结构进行调整。

螺距的选择会影响蜗杆的负载能力、传动效率等性能指标。

蜗杆螺纹螺距计算公式蜗杆螺纹是一种常见的机械传动元件，广泛应用于各种机械设备中。

蜗杆螺纹的螺距是指蜗杆上螺纹的间距，是蜗杆螺纹的重要参数之一。

螺距的大小直接影响到蜗杆螺纹的传动性能和使用效果。

因此，准确计算蜗杆螺纹的螺距是非常重要的。

蜗杆螺纹的螺距计算公式可以通过以下公式来计算：P = π d tan(α)。

其中，P为螺距，d为蜗杆螺纹的直径，α为蜗杆螺纹的螺距角。

螺距是指相邻两个螺纹峰之间的距离，通常用毫米（mm）或英寸（inch）来表示。

螺距的大小直接影响到蜗杆螺纹的传动效果，一般来说，螺距越大，传动效果越好，但是制造成本也会相应增加。

因此，在设计蜗杆螺纹时，需要根据实际情况来合理确定螺距的大小。

螺距的计算需要根据蜗杆螺纹的直径和螺距角来确定。

螺距角是指蜗杆螺纹的斜面与轴线的夹角，通常用tan(α)来表示。

在实际应用中，螺距角的大小一般为5°-25°之间，具体取值要根据蜗杆螺纹的使用要求来确定。

蜗杆螺纹的直径是指蜗杆螺纹的直径尺寸，通常用毫米（mm）或英寸（inch）来表示。

在计算螺距时，需要首先确定蜗杆螺纹的直径和螺距角，然后根据上述公式来计算螺距的大小。

蜗杆螺纹的螺距计算公式可以帮助工程师和设计人员准确计算蜗杆螺纹的螺距，从而更好地满足机械设备的传动需求。

合理确定螺距的大小可以提高蜗杆螺纹的传动效果，降低制造成本，提高机械设备的使用性能。

除了螺距的计算公式外，还需要注意蜗杆螺纹的加工工艺和质量控制。

蜗杆螺纹的加工工艺对螺距的精度和表面质量有着重要影响，因此需要采用合适的加工工艺和设备来保证蜗杆螺纹的质量。

同时，还需要进行严格的质量控制，确保蜗杆螺纹的螺距符合设计要求，从而保证机械设备的正常使用。

总之，蜗杆螺纹的螺距是蜗杆螺纹的重要参数之一，合理计算螺距的大小对于提高蜗杆螺纹的传动效果和使用性能非常重要。

螺距的计算公式可以帮助工程师和设计人员准确计算螺距的大小，从而更好地满足机械设备的传动需求。

蜗轮蜗杆计算蜗杆传动当两根轴在90度相交，但它们既不平行也不相交时，采用蜗轮传动。

在蜗轮传动中，蜗杆是主动部件，蜗轮是被动部件。

蜗轮传动具有以下特点:1)结构紧凑，可获得较大的传动比，一般传动比为7-80。

2)运行稳定，无噪声3)传输功率范围大4)自锁5)传动效率低，蜗轮蜗杆往往由有色金属制成。

蜗杆的螺杆可分为单头螺杆和多头螺杆。

传动比计算公式如下:I = N1 / N2 = Z / KN1为蜗杆转速，N2为蜗轮转速，K为蜗杆头数，Z为蜗轮齿数蜗轮蜗杆机构1、目的:蜗轮蜗杆机构通常用于在两根交错轴之间传递运动和动力。

蜗轮和蜗杆相当于中间平面上的齿轮和齿条，蜗杆和螺杆的形状相似。

\ 二、基本参数：模数m、压力角、蜗杆直径系数q、导程角、蜗杆头数、蜗轮齿数、齿顶高系数（取1）及顶隙系数（取0.2）。

其中，模数m和压力角是指蜗杆轴面的模数和压力角，亦即蜗轮轴面的模数和压力角，且均为标准值；蜗杆直径系数q为蜗杆分度圆直径与其模数m的比值，三、蜗轮蜗杆正确啮合的条件1 中间平面内蜗杆与蜗轮的模数和压力角分别相等，即蜗轮的端面模数等於蜗杆的轴面模数且为标准值；蜗轮的端面压力角应等於蜗杆的轴面压力角且为标准值，即m2 当蜗轮蜗杆的交错角为时，还需保证，而且蜗轮与蜗杆螺旋线旋向必须相同。

四、几何尺寸计算与圆柱齿轮基本相同，需注意的几个问题是：蜗杆导程角()是蜗杆分度圆柱上螺旋线的切线与蜗杆端面之间的夹角,与螺杆螺旋角的关系为，蜗轮的螺旋角，大则传动效率高，当小於啮合齿间当量摩擦角时，机构自锁。

引入蜗杆直径系数q是为了限制蜗轮滚刀的数目，使蜗杆分度圆直径进行了标准化m一定时，q大则大，蜗杆轴的刚度及强度相应增大；一定时，q小则导程角增大，传动效率相应提高。

蜗杆头数推荐值为1、2、4、6，当取小值时，其传动比大，且具有自锁性；当取大值时，传动效率高。

与圆柱齿轮传动不同，蜗杆蜗轮机构传动比不等於，而是，蜗杆蜗轮机构的中心距不等於，而是。

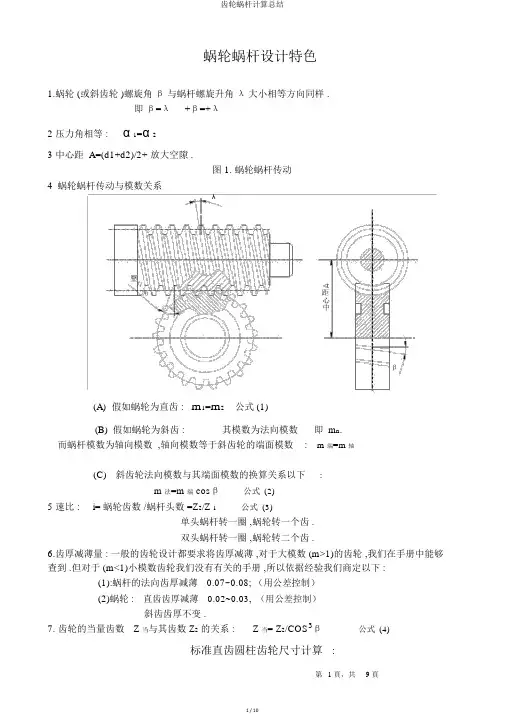
蜗轮蜗杆设计特色1.蜗轮 (或斜齿轮 )螺旋角β与蜗杆螺旋升角λ大小相等方向同样 .即β=λ+β=+λ2 压力角相等 :α 1=α 23 中心距 A=(d1+d2)/2+ 放大空隙 .图 1. 蜗轮蜗杆传动4蜗轮蜗杆传动与模数关系λ壓力角α距心中β(A)假如蜗轮为直齿 : m1=m2公式 (1)(B) 假如蜗轮为斜齿 :其模数为法向模数即m n.而蜗杆模数为轴向模数 ,轴向模数等于斜齿轮的端面模数:m 端=m 轴(C)斜齿轮法向模数与其端面模数的换算关系以下:m 法=m 端 cosβ公式(2)5 速比 :i= 蜗轮齿数 /蜗杆头数 =Z2/Z 1公式(3)单头蜗杆转一圈 ,蜗轮转一个齿 .双头蜗杆转一圈 ,蜗轮转二个齿 .6.齿厚减薄量 : 一般的齿轮设计都要求将齿厚减薄 ,对于大模数 (m>1)的齿轮 ,我们在手册中能够查到 .但对于 (m<1)小模数齿轮我们没有有关的手册 ,所以依据经验我们商定以下 :(1):蜗杆的法向齿厚减薄0.07~0.08; （用公差控制）(2)蜗轮 :直齿齿厚减薄0.02~0.03,（用公差控制）斜齿齿厚不变 .7. 齿轮的当量齿数Z 当与其齿数 Z2的关系 :Z 当= Z2/COS3β公式(4)表 1:标准直齿轮尺寸计算各部分名称代号模数M 压力角 A 分度圆直径 d 分齿顶高h 顶齿根高h 根全齿高H 齿顶圆直径 D 顶齿根圆直径 D 根基圆直径 d 基周节T 分度圆齿厚S 分度圆齿槽厚 A 中心距 A公式依据齿轮须要蒙受的力量定出a=20°d 分1=mZ1 d 分2=mZ2标准齿形 :h 顶=m;短齿:h 顶=0.8m;标准齿形 :h 根=1.25m;短齿:h 根=1.1m;标准齿形 :h=h 顶+ h 根=2.25m;短齿:h=1.9m;D 顶1=m(Z1+2) D 顶2=m(Z2+2)D 根1= m(Z1-2.5) D 根2=m(Z2-2.5)d 基1= d 分1 cos a d 基2= d 分2 cos aT=π m; π=3.1459S=1/2πma=1/2πmA=1/2(d 分1+ d 分2)=1/2m (Z1 +Z2 )当齿轮 m 和 z 已知时 ,从表 1 中可计算出有关尺寸 .例:如附图1所示:已知m=0.6z=18d 分 =mz=0.6*18=10.80d 顶 =m(z+2)=0.6*(18+2)=12.00d 根 =m(z-2.5)=0.6(18-2.5)=9.30标准斜齿轮的计算表 2 标准斜齿轮尺寸计算各部分名称代号分度圆直径 d 分齿顶高h 顶齿根高h 根全齿高H 齿顶圆直径 D 顶基圆直径 d 基端面压力角 a 端端面周节t 端法面周节t 法法面齿厚s 法中心距 A公式d 分1=m 端 Z1= m 法 Z1/cosβ d 分2= m 法 Z2/cosβh 顶=m 法; h 顶=0.8m法; (短齿)h 根=1.25m法; h 根=1.1m法; (短齿 )h=2.25m法; h=1.9m法; (短齿)D = d + 2m法D顶2= d + 2m法顶 1 分 1 分 2d 基1= d 分1 cos a端 d 基2= d 分2 cos a端tg a 端=tg a法/cos βt 端=πd 分/Zt 法=πm 法;s 法=πm 法/2)=m (Z +Z )/2cosβA=1/2(d分 1+ d分法2 12由查表 2 可计算出斜齿轮的有关尺寸例:已知m=0.6α=20°β=10°右旋.(附图 1 中的斜齿轮 )第2頁，共9頁蜗杆的尺寸计算1 对于蜗杆的特征系数 q:q=蜗杆分度圆直径 /模数 m公式 (5)蜗轮一般是用蜗轮滚刀来加工 , 蜗轮滚刀实质上相当于一个开了齿的蜗杆 . 蜗轮滚刀模数同样 , 直径不同样时螺旋升角 λ也不同样 ,也就是说一种蜗轮滚刀不可以加工同样模数的随意齿数的蜗轮 ,需要配好多蜗轮滚刀 .为了减少蜗轮滚刀的数目 ,国家规定了蜗杆特征系数 q.我们在设计蜗杆时应尽量采用标准的蜗杆特征系数 q. q 与 m 的关系如表 3 所示 :表 3 蜗杆特征系数 q模数 m11.5 22.53(3.5) 4(4.5)56(7)8(9) 10蜗杆特数系数 p14 14 13 12 12 12 11 11 10(12) 9(11) 9(11) 8(11) 8(11) 8(11)注 :括号中的数字尽可能不用 ( 当用蜗轮滚刀加工时 ).特征系数 q 与蜗杆分度圆上的螺旋升角 λ的关系 . 如表 4 所示表 4 .特征系数 q 与螺旋升角 λ 的关系 .qZ 1 ° 8 9 10 11 12 13 14 107'30" ° °5°11'40" 4°45'49" 4° 23'55" 4°05'08" 27 6 20'25" 5 42'38"°02'10" °°10° 18'17" 9°27'44" 8° 44'46" 8°07'48"14 12 31'44" 11 18'36" 320°33'22" 18°26' 06" 16°41'57" 15° 15'18" 14°02'10" 12°59'41" 12° 05'41"4° 33'54" 23°57'45" 21°48'05" ° ° °15° 56'43"26 19 58'59" 18 26'06" 17 06'10"在设计蜗杆传动中 .因为我们是将斜齿轮来取代蜗轮的 .所以在设计蜗轮蜗杆传动时 ,能够不受特征系数 q 的限制 .但所设螺旋升角应在表 4 范围内 . 依据表 5 能够算出蜗杆的尺寸 .頂 分L根 分 頂根頂 t 軸S 分弦1hα=20°h 分弦1h根 h图 2.蜗轮蜗杆的主要尺寸表 5 蜗杆的尺寸计算 :.所求参数主要尺寸和参数 :分度圆直径齿顶高齿根高全齿高齿顶圆直径齿根圆直径切制螺纹部分长度螺旋线升角其余计算 .丈量用的参数 :轴向齿距螺牙导程轴向压力角法面压力角螺牙在分度圆上的轴向齿厚螺牙在分度圆上的法向齿厚螺牙在分度圆上的法向弦齿厚丈量S 法分弦1用的齿高符号计算公式d分 1d =mq分 1h 顶h 顶=mh 根h 根=1.2mh h= h 顶+ h 根=2.2m + 2m=m(q+2)D顶D = d分 1+2h根= d顶 1 分 1D 根 D 根1= d 分1-2h 根= d 分1- 2.4m=m(q-2.4)L L=(13 ~16)m 当 Z1=1~2 L=(15 ~20)m 当 Z1=3~4 λtgλ = Z1m/ d 分1=Z1/qT 轴t 轴=πmT T= Z1 t 轴a °a 法a=20tga 法λS轴分1=tgacosS轴分1 = t 轴 /2=π m/2S法分1 S 法分 1 轴分 1 cosλS法分弦1= SS 法分弦1≒ S 法分1≒ S 轴分1cosλH 法分弦1 h 法分弦1=m例:如附图2所示已知端面模数m=0.5Z=2α=20°λ=7.52°右旋其计算以下 :d 分 =Zm/tgλ=2*0.5/tg7.52° =7.58d 顶 =d 分+2m=7.58+2*0.5=8.58d 根 =d 分-2.4m=7.58-2.4*0.5=6.38T=Zt=2*πm=3.14在图纸中还要标出其分度圆法向弦齿厚及法向弦高代入已知参数得 :S 法分弦 =πm/2*COSλ=πx0.5/2*cos7.52°=0.78h 法分弦 =m=0.5依据蜗轮蜗杆传动重点第 6 点 ,取分度圆法向弦齿厚S 法分弦为 0.78 -0.02-0.04注: 对于蜗杆减薄量 ,授课时说是减薄 0.07~0.08.这是依据黄克恭先生的经验定的 ,本例减薄这个数是依据陈坚先生经验定的 ,其经验为 0.02~0.04. 我(孙工 )偏向陈坚先生的减薄量 .蜗轮蜗杆的查验蜗杆的查验一般查验其法向分度圆弦齿厚如附图 2 所示在图纸中要给出法向分度圆弦齿厚和捡验蜗轮 (斜齿轮 )的方法有三种 :(1)捡验公法线长度 ;(2)捡验固定弦齿厚 :(3)捡验分度圆法向弦齿厚这三种方法我们任选一种 .公法线长度的计算捡验公法线长度的方法如图3所示 .公法線長度 (L) L 端基節 (t 基) 基節 (t 基)分度圓基圓齒厚s基L法斜齒端面直齒輪斜齒基圓展開圖图 3.齿轮公法线长度的捡验斜齿轮公法线长度的计算公式: α=20°Q=0.364/COS(? )公式(6)Z’=Z*[Q-0.01745*arctan(Q)]/ 0.0149依据 Z’(四舍五入取整数 ) 查表 6 得跨齿数N公法线长度 L=Mn*[2.9521*(N-0.5)+0.014*Z’] 公式 (7)注意公式 (7)中的 Z’不要四舍五入取整数直齿轮公法线长度可查表 6 得. (表 6 是 m=1 λ=20°时的数值 .)表 6. 标准直齿轮公法线长度 L'齿跨m=1的齿跨M=1 的齿跨M=1 的齿跨m=1的齿齿齿齿数数公法线长数数公法线长数数公法线长数数公法线长Z n L' Z N L' Z N L' Z N L'30 4 10.7526 60 7 20.0292 90 11 32.257931 4 10.7666 61 7 20.0432 91 11 32.271932 4 10.7086 62 7 20.0572 92 11 32.285933 4 10.7946 63 8 23.0233 93 11 32.29994 2 4.4842 34 4 10.8086 64 8 23.0373 94 11 32.31395 2 4.4982 35 4 10.8227 65 8 23.0513 95 11 32.32796 2 4.5122 36 5 13.7888 66 8 23.0654 96 11 32.34197 2 4.5262 37 5 13.8028 67 8 23.0794 97 11 32.35598 2 4.5402 38 5 13.8168 68 8 23.0934 98 11 32.36999 2 4.5542 39 5 13.8308 69 8 23.1074 99 12 35.336110 2 4.5683 40 5 13.8448 70 8 23.1214 100 12 35.350111 2 4.5823 41 5 13.8588 71 8 23.1354 101 12 35.364112 2 4.5963 42 5 13.8728 72 9 26.1015 102 12 35.378113 2 4.6103 43 5 13.8868 73 9 26.1155 103 12 35.392114 2 4.6243 44 5 13.9008 74 9 26.1295 104 12 35.406115 2 4.6383 45 6 16.8670 75 9 26.1435 105 12 35.420116 2 4.6523 46 6 16.8810 76 9 26.1575 106 12 35.434117 2 4.6663 47 6 16.8950 77 9 26.1715 107 12 35.448118 3 7.6324 48 6 16.9090 78 9 26.1855 108 13 38.414219 3 7.6464 49 6 16.9230 79 9 26.1996 109 13 38.428220 3 7.6604 50 6 16.9370 80 9 26.2136 110 13 38.442321 3 7.6744 51 6 16.9510 81 10 29.1797 111 13 38.456322 3 7.6885 52 6 16.9650 82 10 29.1937 112 13 38.470323 3 7.7025 53 6 16.9790 83 10 29.2077 113 13 38.484324 3 7.7165 54 7 19.9452 84 10 29.2217 114 13 38.498325 3 7.7305 55 7 19.9592 85 10 29.2357 115 13 38.512326 3 7.7445 56 7 19.9732 86 10 29.2497 116 13 38.526327 4 10.7106 57 7 19.9872 87 10 29.2637 117 14 41.492428 4 10.7246 58 7 20.0012 88 10 29.2777 118 14 41.506429 4 10.7386 59 7 20.0152 89 10 29.2917 119 14 41.520430 4 10.7526 60 7 20.0292 90 11 32.2579 120 14 41.5344公法线长度 L'.它合用于随意模数的直齿轮. 使用方法是 :L=L'm公式 (8)例查得 :Z=18 时跨齿数为 3L'=7.6324于是L=7.6324*0.6=4.579≒4.58对于直齿轮来说 ,用查表法计算公法线长度比用公式来计算来的方便 .当直齿轮模数小于 0.4时,最好用公法线长度捡验而不用其余方法 ,因为公法线长度便于丈量 .固定弦齿厚的计算图 4 固定弦齿厚的地点图中虚线为齿条齿形 ,固定弦齿厚 S 弦是齿条齿形与齿轮形相切的两点 A 和 B 的长度 .S弦頂圓A弦分度圓Bh齒條公式为 : 当 m=1 时S 弦=1.387m (公式 9)h 弦=0.7476m (公式 10)公式 (9)(10)直斜齿轮公用 ,斜齿轮指法向模数例: 已知m=0.6Z=26α=20°β=10°那么:S 弦=1.387*0.6=0.83h 弦=0.7476*0.6=0.45对于斜齿轮来说不给减薄量,但要给公差如: S弦=0.83-0.03或S弦=0.83-0.02.直齿轮分度圆弦齿厚的计算直齿轮分度圆弦齿厚的计算公式当 m=1 时S 分弦 =1.55688*m公式(11)h 分弦 =1.0342*m公式(12)例 :如附图1已知m=0.6Z=18S 分弦 =1.55688*0.60=0.94h 分弦 =1.0342*0.60=0.62 取: S 分弦 =0.92-0.02h 分弦 =0.62图 5. 直齿轮斜齿轮法向分度圆弦齿厚的计算S 分法弦 =m*Z 当 sin90°/Z 当公式(13)h 分法弦 =0.6[1+(Z 当/2)*(1-cos90°/Z 当)]公式(14)例 :已知:m=0.6Z=26α=20°β =10°代入已知数 : S 分法弦 =0.6*Z 当 sin90° /Z 当=0.94S 分法弦 =0.94-0.02h 分法弦 =0.6[1+Z 当/2(1-cos90°/Z 当)]=0.61Z 当=Z/cos3β=27.2219 =Z当 cos310°=27.2219对于斜齿轮来说S 分法弦不给减薄量但要给公差 ,S 分法弦取 0.94-0.02径克制齿轮尺寸的计算径克制齿轮各部分尺寸的计算,一般是转变成模数来计算.其公式 : m=25.4/DP公式(15)有了模数后 ,就能够利用前方所给的表及公式进行计算 .在齿轮的图纸止要给出 : 径节 DP 齿数Z 压力角λ和螺旋角β,而不用给出模数 .值得指出的是 ,径节 DP 也有端面和法面之分 .对于直齿轮来说 DP 是指端面径节 ,对于斜齿轮来说,DP 是指法面径节 .与径克制斜齿轮相当的蜗杆要用端面径节去计算 .附表 3径克制斜齿轮的计算名称计算公式DPn(法向径节 )DPn=DPs/cosβ=Z/dcosβDPs(端面径节 )DPs=Z/d=Dpncosβtn(法向周节 )tn=tscosβ=πd/ZTs(端面周节 )ts=π /DPsZ(齿数 )Z=DPsd=dDPscosβh(齿全高 )h=2.157/DPn分弦頂圓弦h分分度圓h1 (齿顶高 ) h2 (齿根高 ) D(节径 )D(外径 ) Di( 根径 ) S(弧齿厚 ) β(螺旋角 ) h1=1/DPnh2=1.157/DPnd=Z/DPncosβ =Z/DPs D=d+2/DPnDi=d-2.314/DPnS=1.5708/DPscosβ =Z/DPnd附表 1 齿轮标准模数系列 (JB111-60)0.1 1.0 3.5 9 220.15 1.25 (3.75) 10 250.20 1.5 4.0 (11) 280.25 1.75 4.5 12 300.3 2.0 5.0 (13) 330.4 2.25 (5.5) 14 360.5 2.5 6.0 (15) 400.6 (2.75) (6.5) 16 450.7 3 7 18 500.8 (3.25) 8 20注: 在采用模数时 ,括号内的模数尽可能不用.。

蜗轮蜗杆的传动比计算公式
蜗轮蜗杆传动是一种常用的传动方式，其传动比的计算公式如下：
传动比 = (大蜗轮齿数÷ 小蜗杆齿数) × (小蜗轮齿数÷ 大蜗杆齿数)
其中，大蜗轮和小蜗杆组成一对传动，小蜗轮和大蜗杆组成另一对传动。

在实际应用中，为了保证传动的稳定性和可靠性，需满足以下条件：
1. 大蜗轮和小蜗杆、小蜗轮和大蜗杆的蜗杆蜗轮的啮合角度应当小于等于14度。

2. 大蜗轮和小蜗杆、小蜗轮和大蜗杆的啮合点应当在蜗杆的中心处。

3. 传动中心线要与蜗杆的轴线重合。

以上条件能够保证传动的稳定性和可靠性，并且保证传动比的准确性。

- 1 -。

蜗轮蜗杆滑动速度计算
蜗轮蜗杆传动是机械行业中局限传动比较大的传动方法之一，利
用其传动特点可以实现高扭矩、低速的运动。

在蜗轮蜗杆传动中，滑动速度的计算方法如下：
首先，假设蜗杆的转速为n1，蜗轮的转速为n2，蜗杆的导程角
为α，蜗轮的齿数为Z2。

则蜗轮的滑动速度V2可通过以下式子求得：V2 = π × d2 × (n1/n2) × cosα
其中，d2为蜗轮的分圆直径。

通过这个式子，我们可以得知，在蜗轮蜗杆传动中，当蜗杆的转
速n1越大，蜗轮的滑动速度V2也越大；反之，当蜗轮的齿数Z2越大，则蜗轮的滑动速度V2越小。

通过以上计算公式，我们可以得出蜗轮蜗杆滑动速度的计算结果，供机械设计工程师们参考使用。

3头蜗杆加工计算公式蜗杆传动是一种常见的机械传动方式，它可以将旋转运动转化为线性运动，或者将高速旋转运动转化为低速旋转运动。

在工业生产中，蜗杆传动被广泛应用于各种机械设备中，如提升机、输送机、搅拌机等。

而在蜗杆传动中，3头蜗杆是一种常见的结构形式，它由两个蜗轮和一个蜗杆组成，具有较高的传动效率和承载能力。

在进行3头蜗杆的加工时，需要进行一系列的计算，以确保其性能和精度满足要求。

下面将介绍3头蜗杆加工计算公式及其应用。

1. 蜗杆螺旋角计算公式。

蜗杆的螺旋角是指蜗杆螺旋线与轴线的夹角，它是决定蜗杆传动效率和承载能力的重要参数。

蜗杆的螺旋角一般在5°~30°之间，一般情况下，蜗杆的螺旋角越小，传动效率越高，但承载能力越低。

而螺旋角的计算公式为：tgα = （πd）/（z m）。

其中，α为螺旋角，d为蜗杆的中径，z为蜗杆的齿数，m为蜗杆的模数。

通过这个公式，可以计算出蜗杆的螺旋角，并根据实际要求选择合适的数值。

2. 蜗杆模数计算公式。

蜗杆的模数是指蜗杆螺旋线上相邻两个齿之间的距离，它是决定蜗杆传动精度和承载能力的重要参数。

蜗杆的模数一般根据传动比、传动效率和承载能力来确定，一般情况下，蜗杆的模数越大，传动效率越高，但传动精度越低。

而蜗杆的模数计算公式为：m = （πd）/z。

其中，m为蜗杆的模数，d为蜗杆的中径，z为蜗杆的齿数。

通过这个公式，可以计算出蜗杆的模数，并根据实际要求选择合适的数值。

3. 蜗杆蜗轮传动比计算公式。

蜗杆蜗轮传动比是指蜗杆传动时蜗轮的转速与蜗杆的转速之比，它是决定蜗杆传动速度和扭矩变化的重要参数。

蜗杆蜗轮传动比一般根据实际工作要求来确定，一般情况下，蜗杆蜗轮传动比越大，传动速度越低，但扭矩越大。

而蜗杆蜗轮传动比计算公式为：i = z1/z2。

其中，i为蜗杆蜗轮传动比，z1为蜗轮的齿数，z2为蜗杆的齿数。

通过这个公式，可以计算出蜗杆蜗轮传动比，并根据实际要求选择合适的数值。

蜗杆速比所有计算公式蜗杆速比是指蜗杆传动的速度比，它是蜗杆的周速与蜗轮的周速之比。

在机械传动中，蜗杆传动是一种常见的传动方式，具有结构简单、传动平稳、噪音小等优点，因此在工业生产中得到广泛应用。

在实际应用中，需要根据具体的传动要求来计算蜗杆速比，以确保传动系统的正常运行。

下面将介绍蜗杆速比的计算公式及相关知识。

1. 蜗杆速比的定义。

蜗杆速比（i）是指蜗杆的周速与蜗轮的周速之比，通常用i表示。

蜗杆传动的速比决定了输出轴的转速与输入轴的转速之间的关系，是蜗杆传动设计中的重要参数。

2. 蜗杆速比的计算公式。

蜗杆速比的计算公式可以根据蜗杆传动的结构特点和运动规律来推导，一般有以下几种情况：（1）普通蜗杆传动的速比计算公式。

对于普通蜗杆传动，其速比可以通过以下公式来计算：i = n1 / n2。

其中，i为蜗杆速比，n1为蜗杆的转速，n2为蜗轮的转速。

（2）带有多级传动的蜗杆速比计算公式。

如果蜗杆传动采用多级传动结构，其速比可以通过以下公式来计算：i = (n1 n2 ... nk) / (m1 m2 ... mk)。

其中，i为蜗杆速比，n1、n2、...、nk为各级蜗杆的转速，m1、m2、...、mk为各级蜗轮的转速。

（3）蜗杆速比的理论计算公式。

根据蜗杆传动的原理和运动规律，可以得到蜗杆速比的理论计算公式：i = (z2 π d1) / (z1 π d2)。

其中，i为蜗杆速比，z1为蜗杆的齿数，z2为蜗轮的齿数，d1为蜗杆的分度圆直径，d2为蜗轮的分度圆直径。

3. 蜗杆速比的影响因素。

蜗杆速比的大小直接影响着蜗杆传动的输出转速和扭矩，因此在实际应用中需要考虑以下几个因素：（1）蜗杆的螺旋角度。

蜗杆的螺旋角度决定了蜗杆传动的传动比，通常情况下螺旋角度越大，蜗杆速比越大。

（2）蜗杆与蜗轮的齿数。

蜗杆与蜗轮的齿数决定了蜗杆传动的速比，一般情况下蜗轮的齿数越大，蜗杆速比越大。

（3）蜗杆传动的效率。

蜗杆传动的效率会影响其输出转速和扭矩，需要在计算蜗杆速比时考虑传动效率的影响。

蜗轮蜗杆的传动比计算公式蜗轮蜗杆是一种常见的传动装置，它能够实现大功率的传递和变速。

在设计和应用中，需要计算蜗轮蜗杆的传动比，这样才能确定驱动装置和被驱动装置之间的速度关系。

蜗轮蜗杆的传动比计算公式为：
传动比=蜗轮轴的周长÷蜗杆轴的周长
其中，蜗轮轴的周长指的是蜗轮每个齿的周长之和，而蜗杆轴的周长则是蜗杆每个螺旋线的周长之和。

这两个参数的计算需要根据具体的设计和制造要求进行。

通过计算传动比，可以有效地控制蜗轮蜗杆的转速和扭矩，以满足不同的工作需求。

同时，还可以利用传动比计算出驱动装置和被驱动装置之间的速比，从而实现更精准的传动控制。

涡轮蜗杆中心距离计算公式涡轮蜗杆传动是一种常见的机械传动方式，广泛应用于工业生产中。

在设计和制造涡轮蜗杆传动系统时，确定涡轮蜗杆中心距离是非常重要的一步。

涡轮蜗杆中心距离的大小直接影响到传动系统的效率、稳定性和寿命。

因此，正确地计算涡轮蜗杆中心距离是非常重要的。

涡轮蜗杆传动系统包括两个主要部分，涡轮和蜗杆。

涡轮是一种旋转的机械零件，通常用于将流体（如水或气体）的动能转换为机械能。

蜗杆则是一种螺旋形的齿轮，用于传递动力并改变传动方向。

在涡轮蜗杆传动系统中，涡轮和蜗杆之间的中心距离是非常重要的参数，它决定了传动系统的工作效果。

涡轮蜗杆中心距离的计算公式可以通过以下步骤来确定。

首先，需要确定传动系统的工作参数，包括涡轮和蜗杆的参数，如直径、齿数、齿轮模数等。

其次，根据传动比和传动效率确定涡轮蜗杆的转速比。

最后，根据涡轮蜗杆的转速比和工作参数，可以使用以下公式来计算涡轮蜗杆中心距离：C = (D1 + D2) / 2 + (m1 + m2) / 2。

其中，C表示涡轮蜗杆中心距离，D1和D2分别表示涡轮和蜗杆的直径，m1和m2分别表示涡轮和蜗杆的模数。

这个公式可以用来计算涡轮蜗杆中心距离的大致数值，但在实际应用中，还需要考虑传动系统的工作环境、负载情况等因素，进行适当的修正和调整。

在实际应用中，涡轮蜗杆中心距离的确定需要考虑多种因素。

首先，涡轮蜗杆传动系统的工作环境对中心距离的要求不同。

例如，在高速传动系统中，为了减小传动系统的体积和重量，可以适当缩小涡轮蜗杆中心距离；而在高扭矩传动系统中，为了提高传动系统的稳定性和寿命，可以适当增大涡轮蜗杆中心距离。

其次，涡轮蜗杆传动系统的负载情况也对中心距禿的要求有所不同。

在大负载情况下，为了减小传动系统的磨损和损耗，可以适当增大涡轮蜗杆中心距离；而在小负载情况下，为了减小传动系统的体积和重量，可以适当缩小涡轮蜗杆中心距离。

总之，涡轮蜗杆中心距离的确定是涡轮蜗杆传动系统设计中的重要一步。

蜗轮的计算公式：1传动比=蜗轮齿数×蜗杆头数2中心距离=（蜗轮节圆直径+蜗轮节圆直径）△23.蜗轮的螺距直径=（齿数+ 2）×模数4个蜗轮齿×蜗轮模块5蜗杆螺距直径=蜗杆外径-2×模数6蠕虫导线=π×成分×头数7螺旋角（前角）TGB =（模数×头数）×蜗杆螺距直径基本参数：蜗杆组件m，压力角，蜗杆直径系数Q，导程角，蜗杆头数，蜗杆齿数，齿高系数（1）和间隙系数（0.2）。

其中，模数m和压力角是蜗轮轴表面的模数和压力角，即蜗轮端面的模量和压力角，两者均为标准值。

蜗杆直径系数q是蜗杆分度圆直径与其模量M的比值。

正确啮合蜗轮和蜗杆的条件：在中间平面中，蜗杆和蜗轮的模量和压力角分别相等，即，蜗轮端面的模量等于蜗杆轴线的模量，即标准值。

蜗轮端面的压力角应等于轴向压力角和蜗杆的标准值，即== M.当蜗轮的交角固定时，蜗轮与蜗杆的螺纹方向必须一致。

蜗轮蜗杆结构通常用于在两个交错轴之间传递运动和动力。

蜗轮与中间平面上的齿轮和齿条等效，蜗轮和螺杆的形状相似。

分类这些系列大致包括：1. Wh系列蜗轮减速机：wht / whx / whs / whc2；CW系列蜗轮减速机：CWU / CWS / cwo3；WP系列蜗轮减速机：WPA / WPS / WPW / WPE / wpz / wpd4；TP 系列包络蜗轮减速机：TPU / TPS / TPA / tpg5；PW型平面双包络环形蜗杆减速机；另外，根据蜗杆的形状，蜗杆驱动器可分为圆柱蜗杆驱动器，环形蜗杆驱动器和斜蜗杆驱动器。

[1]组织特征该机构的传动比大于交错斜齿轮机构的传动比。

2.两个齿轮的啮合齿面之间在线接触，其承载能力远高于交错斜齿轮机构。

3.蜗杆传动相当于螺旋传动，即多齿啮合传动，传动平稳，噪音低。

当蜗杆的超前角小于啮合齿之间的等效摩擦角时，该机构具有自锁性能，可以实现反向自锁，即只有蜗杆可以驱动蜗轮，而不能驱动蜗轮。