非定常气动力1

空气动力学课后答案【篇一：空气动力学复习题】txt>第一章低速气流特性1．何谓连续介质？为什么要作这样的假设？2．何谓流场？举例说明定常流动与非定常流动有什么区别。

流场——流体所占居的空间。

定常流动——流体状态参数不随时间变化；非定常流动——流体状态参数随时间变化；3．何谓流管、流谱、流线谱？低速气流中，二维流谱有些什么特点？流线谱——由许多流线及涡流组成的反映流体流动全貌的图形。

流线——某一瞬间，凡处于该曲线上的流体微团的速度方向都与该曲线相应点的切线相重合。

流管——通过流场中任一闭合曲线上各点作流线，由这些流线所围成的管子。

二维流谱——1.在低速气流中，流谱形状由两个因素决定：物体剖面形状，物体在气流中的位置关系。

2.流线的间距小，流管细，气流受阻的地方流管变粗。

3.涡流大小决定于剖面形状和物体在气流中的关系位置。

4．写出不可压缩流体和可压缩流体一维定常流动的连续方程，这两个方程有什么不同？有什么联系？方程可变为：va=c（常数）气流速度与流管切面积成反比例。

方程可变为：适用于理想流体和粘性流体5．说明气体伯努利方程的物理意义和使用条件。

方程表达式: p?1?v2??gh?常量 21?v2?p0?常量2高度变化不大时，可略去重力影响，上式变为：p?即:静压+动压=全压 (p0相当于v=0时的静压)方程物理意义:空气在低速一维定常流动中，同一流管的各个截面上，静压与动压之和（全压）都相等。

由此可知，在同一流管中，流速快的地方，压力（p）小；流速慢的地方，压力（p）大。

方程应用条件1.气流是连续的、稳定的气流（一维定常流）；2.在流动中空气与外界没有能量交换；3.空气在流动中与接触物体没有摩擦或摩擦很小，可以忽略不计（理想流体）；4.空气密度随流速的变化可忽略不计（不可压流）。

图1-7 一翼剖面流谱p1+?v12=p2+?v22=p3+?v32v1a1=v2a2=v3a3v2=200米/秒p2=-3273675帕斯卡v3=83米/秒p3=445075帕斯卡7.何谓空气的粘性？空气为什么具有粘性？空气粘性——空气内部发生相对运动时，相邻两个运动速度不同的空气层相互牵扯的特性。

升力体高超声速飞行器非定常滚转力矩建模研究高清;李建华;李潜【摘要】为了深入研究升力体高超声速飞行器相对薄弱的横侧向稳定性问题，对滚转自由振荡风洞试验数据进行了谱分析，建立了多个气动频率余弦和形式的非定常滚转力矩模型。

由于升力体高超声速飞行器的滚转自由振荡曲线呈现非定常、非线性和一定的周期性特征，且对试验结果的谱分析发现，在多种气动状态下，都存在除机械振动频率外的三个振动频率，将滚转力矩表达为此三个频率余弦和的形式。

该滚转非定常气动力矩数学模型捕捉了试验的基本趋势涵盖了其主要的量值范围，反映了升力体高超声速飞行器横向流场扰流的多尺度和周期性特征。

%Thorough study of lateral stability of hypersonic lifting aircrafts needs exact ex-pression of aerodynamic roll moment.Spectrum analysis is carried out using roll free-oscillation wind-tunnel test data,and a mathematical model of roll moment is proposed as an expression by the sum of the cosine of the main frequencies from spectrum analysis.The roll test curves of hy-personic lifting model present non-linearity,non-steady and periodical characteristics,and the re-sults of spectrum analysis of roll vibration data under several different flow conditions show that they share three main vibration frequencies apart from the mechanical vibration frequency,which indicates that there are three scales of lateral separation or transition inthe flow pari-son of the mathematical model of roll moment constructed with the corresponding aerodynamic test data indicates,this model can capture the primary tendency of test curves,and cover the main magnitude domain of roll aerodynamic moment.The mathematical modelgives prominence to the multi-scale and periodical characteristics of lateral flow field of hypersonic lifting model.【期刊名称】《空气动力学学报》【年(卷),期】2015(000)003【总页数】5页(P392-396)【关键词】升力体;高超声速;滚转力矩;非定常气动力;建模【作者】高清;李建华;李潜【作者单位】中国航天空气动力技术研究院，北京 100074;中国航天空气动力技术研究院，北京 100074;中国航天空气动力技术研究院，北京 100074【正文语种】中文【中图分类】V211.3;O177.7飞行器空气动力学问题的复杂性之一就在于绕流结构的多尺度特征。

飞行器颤振的基本概念颤振是一种自激振动。

如图1所示，地面上的飞机受到扰动后会引起振动，但由于系统阻尼的存在，这种振动便很快衰减直至完全消失。

Time HistoriesStable (A)Neutral (B)图1颤振示意图飞行中的飞机受到扰动后也会引起振动，当飞行速度较小时，由于气动阻尼作用振动衰减很快；当速度增大到一定程度后，振动衰减逐渐减慢；当达到某一飞行速度后，扰动引起的振幅正好保持不变,这一速度便是颤振临界速度，简称颤振速度，而此时的振动频率称为颤振频率。

由于颤振是在其本身运动引起的气动力激励下发生的，所以颤振是一种自激振动。

因此，颤振的定义可表述为：当升力面在气流中以一定速度运动时，在弹性力、惯性力和空气动力的作用下，刚好使它能够维持等幅振荡的一种自激振动。

机翼振动时，作用在机翼上的气动力是非定常气动力。

为简化起见，可只考虑扭角引起的定常气动力。

气动弹性系统的颤振稳定性可从能量输入方面进行定性研究，即研究一个振动周期内具有沉浮和扭转两个自由度的振动机翼上气动力的能量平衡。

图2给出了机翼振动中沉浮和扭转之间的相差为零的情况（沉浮运动向下为正，俯仰运动迎风抬头为正），由图可见，单位振动周期内气动力给机翼的能量为零，所以气动力不会激振机翼。

若弯曲运动超前扭转运动90度，如图3所示，则整个振动周期内气动力都做正功，因而气动力起激励作用使机翼发生颤振。

由此产生的颤振称之为经典的弯扭颤振。

以上分析说明，当机翼的弯曲和扭转之间有适当的相位差时，运动产生的气动力可能对机翼做正功，从而使机翼发生颤振。

图2相位差为0度，气动力所作总功为零图3相位差为90度，气动力所作总功为正值我们知道，当飞机达到颤振速度时，飞机刚好维持等幅振荡状态。

因此在计算颤振速度时，我们只需要知道作简谐运动的飞行器所受的气动力，即频域气动力，就可以了。

这能够使颤振分析得以简化。

当然也可使用任意运动时域气动力进行颤振计算，虽然这种任意运动时域气动力通常可以通过频域气动力转化，但时域气动力模型往往不易获得。

摘要：近年来，随着风电机组容量的不断增大，以及弱风速型机组的发展，在较短的时间内，叶片长度急剧增加，叶片刚度越来越小，柔性越来越大，风电机组的叶片设计必须考虑动气动弹性稳定性。

本文就叶片受力、气动弹性和颤振等问题进行了阐述；通过叶片三心设计原理、复合材料叶片和叶片气动弹性剪裁抑制颤振的一些具体方法进行了介绍。

关键词：叶片断裂；颤振；叶片三心设计原理；复合材料叶片；气动弹性裁剪0引言风电机组轴承开裂和叶片断裂事件时有发生。

有的机组在投运后很短的时间就出现了叶片断裂，更有甚者，在并网风速远低于切除风速的情况下，刚投运几天的运行机组就出现了叶片断裂问题。

在地球表面形成的风属于不均匀流，机组运行时，风速随机变化，整个叶轮平面内气流的压强、速度、温度和密度等物理量都随时间不断改变，叶轮工作气流的流动属于极其复杂的非定常流动。

在整个叶轮平面内，风的横向、纵向切变较大，风况变化很快，且缺乏足够的检测风速、风向和叶片振动传感器，因此，当运行机组出现叶片断裂时，难以准确了解叶片断裂时的叶轮风况条件，从而难以确切监测到叶片断裂时的振动状况。

大型风电机组是一个复杂的流－固耦合系统，当风电机组在自然风条件下运行时，作用在机组上的空气动力、其自身惯性力和弹性力等交变载荷会使结构产生变形或振动，进而对来流产生影响。

因而叶片在结构设计时，其不仅需要满足强度和刚度要求，还必须降低叶片振动。

风电机组在较宽的工作范围运行(风速范围3～25m/s)。

风速较高时，气流攻角会很大。

因此，机组叶片发生颤振的可能性较大。

一旦叶片颤振发作，就会产生大振幅的剧烈振动。

颤振是当升力面在气流中以一定速度运动时，在气动力、惯性力及弹性力耦合作用下，刚好使物体能够维持等幅振荡的一种自激振动。

气动弹性不稳定性现象主要是颤振，对于叶片来说主要是颤振临界速度及颤振频率的研究。

目前国内外对风电机组叶片的动气动弹性问题的研究尚不多。

随着机组容量的不断增加,叶轮直径加大,尤其是“弱风速型机组”及海上机组的开发，在较短的时间内，叶片长度急剧增加，叶片的刚度越来越小，柔性越来越大。

基于SCI／ERA方法的高效气动力降阶模型窦怡彬;徐敏;Christian Breitsamter【期刊名称】《计算力学学报》【年(卷),期】2012(029)001【摘要】The Walsh-single-composite-input signals based on orthogonal Walsh function were simultaneously inputted into the CFD （Computational Fluid Dynamics） model,using SCI/ERA（Single-Composite- Input/Eigensystem Realization Algorithm） to identify a discrete-time-domain,unsteady aero-dynamic reduced-order-model （ROM） in state space formulation from CFD responses directly. The Isogai wing stand aeroelastic example was computed, and the results demonstrate that the SCI/ERA method decreases model＇s dimension in 2 orders while still maintains the same accuracy of unsteady CFD codes. Compared to Pulse/ERA method,it improves the computational efficiency by 24% and saves memory space by a4 %. Besides, the SCI/ERA method needs much less additional computational resources than Pulse/ERA method while increasing the coupled structure modes. The frequency-domain BPOD（Balanced Proper Orthogonal Decomposition） method can extract a low frequency second-reduced-order-model（SROM） from ROM while remains the same accuracy. The dimension of ROM further decreases by 88% after second order reduction.%由正交Walsh函数构造Walsh-单信号-复合-输入，对其作用下的计算流体力学响应采用单信号-复合-输入／特征系统实现算法SCI／ERA（Single-Composite-Input／Eigensystem Realization Algorithm）辨识得到离散时间非定常气动力状态空间降阶模型。

流场：运动流体所占据的空间。

非（定）常流动：流线的形状和位置（不）随时间变化的流动。

流线：在稳定流动中，流场中每点都与速度矢量相切的曲线。

迹线：流体微团在流场中的运动的轨迹。

流管：通过流场中任一闭合曲线C（不是流线且包含流量）上各点作流线，由这些流线所围成的管子。

流谱：由许多流线及涡线组成的反映流体流动全貌的图形。

全压：静压（P）与动压(PV^2/2)之和。

粘性流体：有粘性的实际流体。

理想流体：粘性系数等于零的流体。

附面层：流体绕固态物体流动时在紧挨着物体壁面附近形成的粘性流体薄层。

转捩点：层流附面层与紊流附面层之间有一个过渡区，通常把它看成是一点。

分离点：附面层气流开始离开翼面的点。

相对弯度：最大弧高中的弧度与弦长的比。

相对厚度：翼型的最大厚度与弦长的比。

展弦比：展长与平均弦长之比。

根尖比：翼根弦长与翼尖弦长之比。

后掠角：机翼上有代表性的等百分弦线（如：前缘线、1/4弦线、后缘线）在XOZ平面上的投影与OZ轴之间的夹角。

迎角：翼弦与相对气流方向之间的夹角。

压力中心：机翼升力的作用点（升力作用线与翼弦的交点）。

压力系数：剩余压力与远前方气流动压之比。

剩余压力：气流静压与大气压力之差。

临界迎角：升力系数最大的迎角。

零升迎角：升力系数等于零的迎角。

升力系数斜率：增加单位迎角时的升力系数的增量。

摩擦阻力：气流与飞机表面发生摩擦形成的阻力。

压差阻力：由于空气粘性作用导致机翼前后压力不等而形成的阻力。

诱导阻力：由升力诱导而产生的阻力。

翼尖涡：由于空气的粘性作用及旋涡的相互作用，旋涡面在翼后不远处卷成两个大涡索。

侧滑：飞机对称面同相对气流方向不一致的飞行。

侧滑角：相对气流方向同飞机对称面之间的夹角。

升阻比：同一迎角下升力与阻力的比值。

总空气动力：飞机升力和阻力的合力。

有利迎角：升阻比最大的迎角。

飞机极线：横坐标表示阻力系数，纵坐标表示升力系数，迎角为参变量，把升力系数和阻力系数随迎角变化的规律用一条曲线表示出来，这条曲线叫做飞机极线。

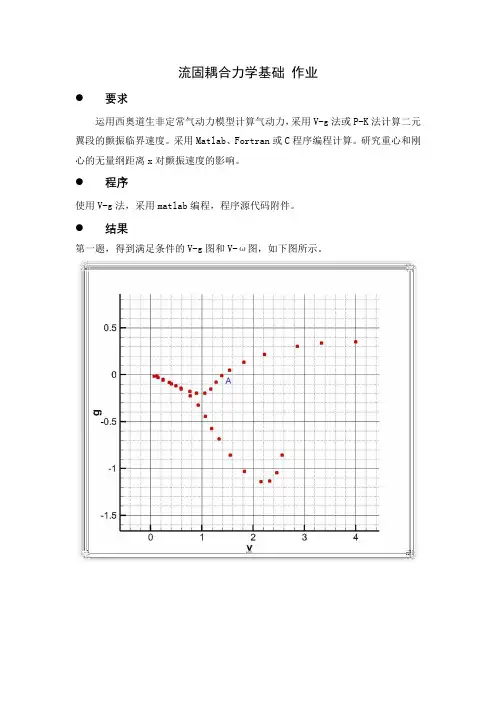
飞行力学课后答案
1、飞行力学课后答案：
(1) 空气动力学原理：空气动力学是航空工程科学的一个分支，
其研究的内容包括流体属性、空气动力学原理、流体动力学原理及它
们在航空器设计、性能参数计算、所产生的空气动力学效应。

其数学
模型包括满足伯努利方程的表示空气动力学原理的非定常流体动力学
的基本方程组。

(2) 机翼和机身的空气动力特性：机翼和机身的空气动力特性是
理解机体行为运动的重要基础，它们包括机翼和机身各种不同空气动
力特性，如流场形态、抗风滑移特性、控制面特性和控制杆特性，以
及机翼和机身抵御气动力的特性。

(3) 机翼的结构和材料：机翼的结构对机翼的外形、几何尺寸和
气动力特性都有着决定性的影响，因此空气动力学课程中重点讲述的
是机翼的结构设计和选择材料的方法及其在飞机结构中的作用。

(4) 飞行控制系统：飞行控制系统是飞机安全和正确飞行的关键，控制系统包括机膜控制系统、机载数据采集系统、控制力学模型、控
制算法和状态构型等，其中包括机身姿态控制和机翼滑移控制两个重
要组成部分，而这两部分要求的空气动力学特性也不尽相同。

(5) 动力学突变：动力学突变广泛存在于飞行力学中，与之对应
的是控制理论，以帮助提高机体的运动精度、控制特性和灵敏度，减
少空气动力学中的不确定性。

为了更好地掌握动力学突变的表现，空
气动力学课程中还介绍了动力学突变的持久型滑移控制、瞬变型控制、机身滑移控制、跟踪控制等内容。

基于非定常 CFD 的俯仰动导数计算方法伍彬;陆韵;周志超;傅建明【摘要】Based on solving N-S equations , the numerical prediction method of pitching dynamic derivatives was studied .The effects of transient time-step, inner iterations , forced sinusoidal motion amplitude and reduced frequency on the calculation result of pitching dynamic derivatives were analyzed . Prediction of dynamic derivatives was conducted for the standard model of dynamic derivatives .The result shows that the transient time-step and reduced frequency are the most important factor affecting dynamic derivatives prediction .The general principle of choosing transient time-step and reduced frequency was presented .The calculation method of pitching dynamic derivatives based on unsteady CFD has high accuracy ,and the result accords with the experiment data .The method has practical value .%采用基于N－S方程求解的非定常CFD技术，对俯仰动导数数值计算方法进行了研究。

柔性翼型的气动弹性建模与颤振特性分析尹维龙;田东奎【摘要】运用Hamilton原理推导了柔性翼型的沉浮-俯仰-弦向弯曲三自由度运动方程,给出了考虑弦向弯曲变形的平板薄翼作简谐运动时非定常气动力的解析表达式,建立了柔性翼型的气动弹性模型.在此基础上,研究了柔性平板薄翼的颤振特性.结果表明：对于平板薄翼而言,单一的弦向弯曲运动是不稳定的.对于给定的沉浮和俯仰振动频率,平板薄翼的颤振速度和其弦向弯曲振动频率有着很大关系.当弦向弯曲振动频率小于俯仰振动频率时,发生颤振的是弦向弯曲分支,颤振速度远小于沉浮-俯仰经典模型的预测值;当弦向弯曲振动频率为俯仰的2.5倍时,弦向弯曲和俯仰分支同时发生颤振;当弦向弯曲振动频率大于俯仰的2.5倍时,发生颤振的分支转为俯仰;当弦向弯曲振动频率大于俯仰的5倍时,沉浮-俯仰-弦向弯曲模型与传统二自由度模型的预测值几乎相等.%The governing differential equations of motion for flexible aerofoil, which is coupled with plunge, pitch, and camber bending motions, were derived by using the Hamilton' s principle. The nonlinear aerody- namic forces of oscillating thin aerofoil were given with consideration of camber bending. The two-dimensional aeroelastic model of flexible aerofoil was presented and the flutter characteristics of flexible thin aerofoil were investigated. Numerical results show that the single camber bending motion is instability. When the character- istic frequencies of pitch and plunge modes are given, the flutter velocity is powerfully affected by the charac- teristic frequency of camber bending mode. When the characteristic frequency of camber bending mode is less than one of pitch mode, the flutter is dominated by the camber bending mode and theflutter velocity is much lower than one given by the classical pitch-plunge coupled model. When the ratio of characteristic frequencies of camber bending and plunge modes is 2.5, the flutter is dominated by the camber bending and plunge modes. When the ratio is greater than 2.5, it is dominated by the plunge mode. When the ratio is greater than 6.0, the pitch-plunge-camber bending coupled aeroelastic model is agreed with the pitch-plunge model.【期刊名称】《哈尔滨工业大学学报》【年(卷),期】2012(044)009【总页数】5页(P69-72,117)【关键词】柔性翼型;气动弹性;弦向弯曲;颤振;非定常气动力【作者】尹维龙;田东奎【作者单位】哈尔滨工业大学复合材料与结构研究所,哈尔滨150080;哈尔滨工业大学复合材料与结构研究所,哈尔滨150080【正文语种】中文【中图分类】V215.3气动弹性问题几乎伴随着航空飞行器发展的全过程，尤其在现代飞机的设计过程中占有非常重要的地位［1］.从早期的二元机翼－舵面系统［2］到今天的大展弦比复合材料柔性机翼［3－5］，气动弹性问题的分析方法越来越成熟，分析手段也越来越丰富，但在气动弹性的分析过程中，研究人员一直沿用“机翼剖面本身是刚性的”这样的一个假设条件.对于传统飞行器而言，机翼的中央翼段和控制面(包括副翼和前、后缘襟翼)沿着翼弦方向的刚度是非常大的，这个假设条件是可以满足的.近些年来，随着智能材料和柔性结构技术的快速发展，机翼不但在翼展方向的刚度设计越来越趋向于柔性化，而且在翼弦方向的刚度也越来越低，如NASA的任务自适应机翼［6］.柔性自适应机翼主要依靠机翼翼面自身的变形来改变机翼弯度和扭转角，以提供几乎理想的机翼弯度形状.该机翼已安装在F－111上进行了多次飞行验证，效果良好.随后，又出现多种不同结构形式的柔性控制面［7－10］.由于柔性控制面的引入，机翼弦向弯曲刚度急剧降低，弦向的弯曲变形对机翼气动弹性问题的影响愈来愈显著.传统的气动弹性模型已不能适用于这类机翼了，不得不考虑机翼弦向弯曲刚度的影响.R.Palacios等［11－12］研究了弦向弯曲变形对机翼静气动弹性变形的影响，但关于考虑弦向弯曲自由度在内的柔性翼型和机翼的动气动弹性问题的研究还比较少.本文主要建立了柔性翼型(是指弦向柔性的翼型)的气动弹性模型，进而研究弦向弯曲刚度对二元翼段颤振特性的影响.柔性翼型的结构模型如图1所示.弦长为2b，来流速度为V.翼型的沉浮位移为h(向下为正)，俯仰角度为α(抬头为正)，弦向弯曲形函数为ψ，弯曲位移为β(上弯为正)，刚心距离位于翼弦中点后ab处.此结构模型包含沉浮和俯仰两个刚体自由度和弦向弯曲自由度.翼段上任一点的位移为整个翼段的动能变分为整个翼段的势能包括拉伸弹簧储存的势能、扭转弹簧储存的势能和弦向弯曲变形所储存的势能.式中:Kh为拉伸弹簧系数;Kα为扭簧的弹簧系数;Kβ为等效的弦向弯曲刚度系数. 势能变分为气动力所作功的变分为运用Hamilton原理，推导二元翼段的运动方程.Hamilton原理的表达式为代入式(2)，整理得到二元翼段的运动方程为式中:Δp为压差.在机翼颤振分析时需要利用非定常空气动力模型.Theodorsen在20世纪30年代末给出了二元平板机翼作简谐振动时非定常气动力的解析表达式，推导过程中假定翼型剖面本身是刚性的.考虑弦向弯曲变形的影响，则二元平板薄翼作简谐振动时旋涡对平板上任一点的诱导速度为将式(1)代入式(3)，得由文献［13］可以推导出沉浮－俯仰－弦向弯曲三自由度二元平板薄翼作简谐振动时非定常气动力的解析表达式.对于等厚平板薄翼，弦向弯曲振动的形函数可取为2次曲线，即当机翼作简谐振动，即则非定常广义气动力为式中:μ=m/(πρab2)为质量比;C(k)为Theodorsen 函数;k= ωb/V 为减缩频率，Lh、Lα、Mh、Mα分别为辅助系数［15］.V-g法是颤振分析使用最广泛的方法之一.在这个方法中，需要引入人工结构阻尼，即式中:gh、gα、gβ分别为人为引入的沉浮、俯仰和弦向弯曲自由度的人工结构阻尼系数.取gh=gα =gβ =g，则有求解式(4)的特征值问题，可以得出颤振频率和颤振速度.假定材料为各向同性材料，则平板薄翼的结构系数为对于平板薄翼，主要考虑3个自由度，即:沉浮、俯仰和弦向弯曲.单个自由度的人工结构阻尼系数为图2为平板薄翼单个自由度的V-g曲线.其中，g为无量纲阻尼系数.由图2可以看出，对于平板薄翼而言，沉浮和俯仰运动是稳定的，而弦向弯曲运动是不稳定的. 由gβ=0，得出弦向弯曲运动的颤振临界减缩频率和速度为式中:kF≈1.07.由式(5)可知，平板薄翼弦向弯曲运动的颤振临界速度是和其弯曲振动频率成正比的.图3为由沉浮－俯仰气动弹性模型得到的平板薄翼V-g曲线.可以看出，由经典气动弹性模型所预测的平板薄翼无量纲颤振速度为2.18，发生颤振的是俯仰(也称为扭转)分支.图4为不同弦向弯曲刚度的平板薄翼颤振速度随着弦向弯曲振动频率的变化曲线.可以看出，当弦向弯曲振动频率小于俯仰振动频率时，机翼的无量纲颤振速度是随着弦向弯曲频率的增加而增加的.当弦向弯曲振动频率小于沉浮振动振动频率时，沉浮－弦向弯曲模型与沉浮－俯仰－弦向弯曲模型的分析结果很接近，此时俯仰自由度可以忽略.V-g图中的颤振分支在颤振点处的斜率反映了颤振的突发程度，曲线斜率越大，表示颤振的突发性越大.从图4中可以看出，当弦向弯曲振动频率小于俯仰振动频率时，弦向弯曲分支在颤振点处的斜率比较大，也就是说，发生颤振的突发性比较大. 对于平板薄翼而言，如果要求弦向弯曲刚度的降低不影响机翼的颤振速度(即由沉浮－俯仰两自由度模型所预测的结果)的话，那么弦向弯曲振动频率不能低于扭转振动频率的2.6倍(即图4中实黑线与虚线交叉点的横坐标值).否则，由于弦向弯曲刚度的降低，机翼的颤振速度将随之降低.因此，柔性自适应机翼的结构设计中要综合考虑弦向弯曲刚度的影响.1)对于平板薄翼而言，单一的弦向弯曲运动是不稳定的，其颤振临界速度是和其弯曲振动频率成正比的.2)当弦向弯曲振动频率小于俯仰振动频率时，发生颤振的是弦向弯曲分支，且该分支发生颤振的突发性比较大;颤振速度是随着弦向弯曲频率的增加而增加的.3)当弦向弯曲振动频率接近俯仰振动频率时，发生颤振的仍然是弦向弯曲分支，颤振速度急剧降低，但颤振的突发性变小了.4)当弦向弯曲振动频率高于俯仰振动频率的2～3倍时，沉浮－俯仰－弦向弯曲模型所预测的颤振速度略高于沉浮－俯仰模型的预测值;当弦向弯曲振动频率为俯仰振动频率的2.5倍时，弦向弯曲和俯仰分支同时发生颤振，但俯仰分支发生颤振的突发性更大;当弦向弯曲振动频率大于俯仰振动频率的2.5倍时，发生颤振的分支转为俯仰.5)弦向弯曲频率大于俯仰频率的5倍时，发生颤振的是俯仰分支，颤振速度逼近沉浮－俯仰模型的预测值，可以不考虑弦向弯曲自由度的影响.【相关文献】［1］陈桂彬，邹丛青，杨超.气动弹性设计基础［M］.北京:北京航空航天大学出版社，2004:99－100.［2］THEODORSEN T.General theory of aerodynamic instability and the mechanism of flutter［R］.NACA －496，1935.［3］冷佳桢，谢长川，杨超.水平弯曲刚度对大展弦比机翼颤振的影响［J］.北京航空航天大学学报，2009，35(6):718－722.［4］刘湘宁，向锦武.大展弦比柔性复合材料机翼的气动弹性剪裁［J］.北京航空航天大学学报，2007，35(6):1404－1408.［5］JOSEPH A G.Numerical investigation of nonlinear aeroelastic effects on flexible high aspect ratiowings［J］.Journal of Aircraft，2005，42(4):1025 －1036.［6］WILLIAM W G.Mission adaptive wing system for tactical aircraft［J］.Journal of Aircraft，1981，18(7):597－563.［7］YIN Weilong，SUN Qijian，ZHANG Bo，et al.Seamless morphing wing with SMP skin［J］.Advanced Materials Research，2008，(47－50):97－100.［8］YIN Weilong.Stiffness requirement of flexible skin for variable trailing-edge camber wing［J］.Science China Technological Sciences，2010，53(4):1077 －1081.［9］LIU Shili，GE Wenjie，LI Shujun.Optimal design of compliant trailing edge for shape changing［J］.Chinese Journal of Aeronautics，2008，21(2):187 －192.［10］DAYNES S，NALL S J，WEAVER P，et al.Bistable composite flap for an airfoil ［J］.Journal of Aircraft，2010，47(1):334－338.［11］PALACIOS R，CESNIK C.Low-speed aeroelastic modeling of very flexible slender wings with deformable airfoils［C］//Proceedingsofthe 49th AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics and Materials Conference.Schaumburg:Illinois，2008:1 －10.［12］PALACIOS R，CESNIK C E S.On the one-dimensional modeling of camber bending deformations in active anisotropic slender structures［J］.International Journal of Solids and Structures，2008，45(7/8):2097 －2116.［13］FORSCHING H W.气动弹性力学原理［M］.沈克扬，译.上海:上海科学技术文献出版社，1982:240－250.［14］赵永辉.气动弹性力学与控制［M］.北京:科学出版社，1997:118－119.。