下载文档原格式
逻辑电路乘法器逻辑电路乘法器是一种能够实现两个二进制数相乘的电路。
在计算机和数字电子系统中，乘法器是非常重要的组成部分，其功能是进行乘法运算，实现数字信号的乘法操作。
乘法器的设计和优化对于系统的性能和功耗都有着重要的影响。
乘法器的实现可以采用不同的方法和结构，具体的实现方式有部分乘法器、全加器乘法器、Booth编码乘法器等。
这些乘法器的共同目标是通过逻辑门电路的组合和时序控制，使得输入的两个二进制数经过运算后得到正确的乘积。
乘法器的设计需要考虑的因素包括速度、面积和功耗等。
部分乘法器是一种基本的乘法器结构，其原理是将两个二进制数的每一位进行逻辑与运算，将结果相加得到最终的乘积。
全加器乘法器是一种改进的乘法器结构，通过使用全加器和加法器来实现部分乘法器中的逻辑与运算和相加操作。
Booth编码乘法器是一种高效的乘法器结构，通过对乘数进行编码，减少了运算的次数，提高了乘法器的效率。
乘法器的设计和优化需要考虑多个方面的因素。
首先是乘法器的运算精度，即乘法器能够处理的位数。
通常情况下，乘法器的运算精度越高，所需的逻辑门电路和时序控制的复杂度就越高。
其次是乘法器的速度，即乘法器能够完成乘法运算的时间。
速度是乘法器设计中一个非常重要的指标，对于需要高速计算的应用，需要采用更快的乘法器结构。
此外，乘法器的面积和功耗也是需要考虑的因素，面积越小和功耗越低的乘法器结构可以降低系统的成本和能耗。
乘法器在数字电子系统中有着广泛的应用。
在计算机的处理器中，乘法器是一个重要的功能模块，用于实现浮点数运算和乘法指令。
在通信系统中，乘法器被用于信号处理和调制解调等关键环节。
在图像和音频处理中，乘法器被用于实现滤波和变换等操作。
乘法器的设计和优化对于系统的性能和功耗都有着重要的影响。
逻辑电路乘法器是一种能够实现两个二进制数相乘的电路。
乘法器的设计和优化对于系统的性能和功耗都有着重要的影响。
乘法器的实现可以采用不同的方法和结构，包括部分乘法器、全加器乘法器和Booth编码乘法器等。
乘法器工作原理
乘法器是一种电子设备，用于实现两个数字（或模拟）信号的乘法运算。
其工作原理可以简单地描述如下：
1. 输入信号：乘法器通常有两个输入端，分别用于接收待相乘的数字信号A和B。
2. 位展开：乘法器将输入信号A和B进行位展开操作，即将
每一个输入位（或字节）进行分离和独立处理。
这可以通过触发器、逻辑门电路等实现。
3. 部分乘积计算：对每一对输入位进行乘法运算，并将结果存储在部分乘积寄存器中。
这可以通过加法器电路来实现，其中每一个乘积被加到累加器中。
4. 乘积累加：将所有的部分乘积相加得到最终的乘积结果。
这可以通过多级加法器电路来实现。
一般来说，乘法器采用树形结构或布斯-舍乘法算法（Booth's algorithm）来提高计算效率。
5. 结果输出：输出端给出乘法运算的结果。
根据需求，这个结果可以是数字信号，模拟电压或电流等形式。
乘法器的工作原理可以根据底层电路和算法的不同而有所变化。
现代的乘法器采用复杂的电路设计和优化算法，以实现更高的运算速度和精度。
定点原码二位乘法器的设计定点原码二位乘法器是一种用于计算机中定点数的乘法操作的电路或逻辑器件。
在计算机中，定点数是以固定小数位数和整数位数表示的数字。
定点原码乘法器可以实现定点数之间的乘法运算，这对于一些计算机应用非常重要，如数字信号处理、图像处理和数值计算等。
1.电路模块划分：定点原码二位乘法器可以划分为多个电路模块，如部分积生成器、积累器、符号位处理器、溢出判断器等。
每个模块要根据功能设计相应的电路和逻辑。
2.全加器设计：全加器是定点二位乘法器中的核心电路模块。
它用于进行两个二进制位相加，并输出相加结果和进位。
全加器可以使用门电路和触发器进行实现。
在设计全加器时，需要考虑到功耗、速度和面积等因素。
3.流程控制设计：定点原码乘法器的计算过程可以划分为多个时钟周期。
在每个时钟周期内，需要按照特定的顺序对电路模块进行控制。
流程控制的设计需要考虑到时序逻辑和状态机的应用。
4.精度控制设计：定点原码乘法器的乘法结果可能会造成溢出或截断。
为了保证计算结果的精度，需要设计相应的溢出判断器和截断处理器。
溢出判断器可以通过比较定点数的符号位来实现，而截断处理器可以使用位移操作实现。
5.优化设计：在定点原码二位乘法器的设计过程中，可以采用一些优化策略来提高性能和减小电路面积。
例如，可以使用逻辑门和触发器的级联来减小时延，使用布线优化来减小电路面积。
总结来说，定点原码二位乘法器的设计需要考虑到电路模块划分、全加器设计、流程控制设计、精度控制设计和优化设计等因素。
通过合理的设计和优化，可以实现高效、准确和可靠的定点数乘法运算。
补码一位乘的booth算法布斯算法是一种计算机算术中使用的乘法算法，其可以有效地计算两个二进制数的乘积。
相比于传统的乘法算法，布斯算法的优势在于减少了乘法器的运算次数，从而提高了计算速度和效率。
布斯算法的核心思想是利用位运算和补码运算，将乘法运算转化为加法运算。
布斯算法中使用的补码乘法是一种对乘法操作进行优化的技术。
具体步骤如下：1.初始化：将需要进行乘法运算的两个二进制数A和B转化为对应的补码形式，即A'和B'。
2.设置两个变量：乘法器寄存器P和乘法操作寄存器E。
3.进行循环：进行n次迭代，其中n为乘法器P的位数，并且每次迭代中右移乘法器寄存器P一位。
4.判断乘法器P的最后一位和倒数第二位的值：-如果最后一位为0，倒数第二位为1，执行步骤5-如果最后一位为1，倒数第二位为0，执行步骤6-如果最后两位都为1或都为0，则进行下一次迭代。
5.步骤5执行以下操作：-将乘法器寄存器P右移一位，并将乘法操作寄存器E与乘数A'相加，得到新的乘法操作寄存器E。
-计数器减16.步骤6执行以下操作：-将乘法器寄存器P右移一位，并将乘法操作寄存器E与乘数A'的补码相加，得到新的乘法操作寄存器E。
-计数器减17.如果计数器为0，则迭代完成，得到最终的乘法操作寄存器E的补码形式，即乘积的补码。
8.将结果转化为原码形式，即得到最终的乘积。
如果结果为负数，则取其补码形式。
布斯算法的优点在于减少了乘法器的运算次数，从而提高了计算速度和效率。
此外，由于布斯算法的乘法运算是通过加法运算来实现的，可以直接使用加法器来进行计算，进一步简化了硬件设计。
不过，布斯算法的实现较为复杂，需要进行多次位运算和补码运算，因此对计算资源的消耗较大。
总结起来，布斯算法是一种利用位运算和补码运算来优化乘法运算的算法。
通过减少乘法器的运算次数，布斯算法提高了计算速度和效率，但是实现较为复杂，对计算资源的消耗较大。
布斯算法在计算机算术中得到了广泛的应用，特别是在乘法器设计和数字信号处理中有着重要的作用。
booth编码原理
Booth编码是一种用于乘法运算的编码方式，最早由A. D. Booth在1951年提出。
Booth编码原理是通过将乘数m分解为n位二进制数的形式表示，其中n是乘数的位数。
这种表示方式中，可用三种编码值来表示每一位：
- "+"，表示为+1
- "0"，表示为0
- "-"，表示为-1
然后，使用Booth编码算法来进行乘法操作：
1. 初始化乘积p为0，保存上一次的编码值s为0。
2. 根据输入的乘数m的最低位，在乘积p的右边加上m的编码。
3. 根据s和当前编码值相乘的结果来决定下一步的操作：
- 如果s和当前编码值相乘结果为1，则向右移动一位，并将m的编码复制到右边。
- 如果s和当前编码值相乘结果为-1，则向右移动一位，并将m的负编码复制到右边。
- 如果s和当前编码值相乘结果为0，则只向右移动一位，不做其他操作。
4. 重复步骤3，直到乘积p的左边n位都为0。
最后，乘积p的右边n位就是最终的结果。
需要注意的是，在计算过程中，p和s都可能为负数，因此需要对结果进行适当
地修正。
Booth编码原理可以减少乘法运算的时钟周期数和乘法器的硬件复杂性，有利于提高乘法运算的效率。
【计算机组成原理】定点乘法运算之补码一位乘法（Booth 算法）(对初学者的步骤详解)【计算机组成原理】定点乘法运算之补码一位乘法（Booth算法）(对初学者的步骤详解)运算规则符号位参与运算，运算的数均以补码表示。
被乘数一般取双符号位参与运算，部分积取双符号位，初值为0，乘数可取单符号位。
乘数末位增设附加位yn+1y_{n+1}yn+1?，且初值为0。
根据(yn,yn+1)(y_{n},y_{n+1})(yn?,yn+1?)的取值来确定操作，参见下表，移位按补码右移规则进行按照上述算法进行n+1步操作，但第n+1不再移位(共进行n+1次累加和n次右移)，仅根据yny_nyn?与yn+1y_{n+1}yn+1?的比较结果做相应的运算。
yny_nyn?(高位)yn+1y_{n+1}yn+1?(低位)部分积右移一位部分积加[X]补[X]_{补}[X]补?，右移一位部分积加[?X]补[-X]_{补}[?X]补?，右移一位部分积右移一位步骤详解无题言狗？？放狗，不对，看题。
设机器字长为5位（含1位符号位，n=4），x=-0.1101，y=0.1011，采用Booth算法求X?YX?YX?Y首先，列出对应的补码。
[X]补=11.0011[X]_{补}=11.0011[X]补?=11.0011[?X]补=00.1101[-X]_{补}=00.1101[?X]补?=00.1101[Y]补=0.1011[Y]_{补}=0.1011[Y]补?=0.1011开始按照要求求解高位部分积位数对标被乘数X的位数，且符号位取双位：部分积：00.0000（高位部分积）（低位部分积-乘数）0.1011|0 丢失位初始情况+[?X]补+[-X]_{补}+[?X]补? 00.1101发现是10所以对照表格，应该部分积加[?X]补[-X]_{补}[?X]补?，右移一位执行本行左边的操作右移一位 00.011010.101|10我们把高位和低位作为一个整体进行右移，所以高位最右边的1到了低位部分的最左边右移一位 00.001101.010|110看见上一行的是11所以直接右移一位+[X]补+[X]_{补}+[X]补? 11.0011是01所以部分积加[X]补[X]_{补}[X]补?，右移一位和：11.0110001.010|110开始右移右移一位 11.10110010.1|0110因为高位部分在补码中，最高位是1时右移补1+[?X]补+[-X]_{补}+[?X]补? 00.1101部分积加[?X]补[-X]_{补}[?X]补?，右移一位和：00.10000010.1|0110开始右移右移一位 00.010000010.|10110是01所以部分积加[X]补[X]_{补}[X]补?，右移一位+[X]补+[X]_{补}+[X]补? 11.0011和 11.0111最后一步不再移位所以蓝色部分构成[X?Y]补=1.01110001[X?Y]_{补}=1.01110001[X?Y]补?=1.01110001,所以X?Y=?0.10001111X?Y=-0.10001111X?Y=?0.10001111根据规则，我们给乘数Y增设附加位yn+1y_{n+1}yn+1?，且初值为0,提供了图表中的初始情况下的1|0课后题：上述的情况是我们[X?Y][X?Y][X?Y]，那么我们计算一下[Y?X][Y?X][Y?X],就可以知道我们是不是掌握了啦！！！课后题解答既然是课后题就不写那么详细啦。
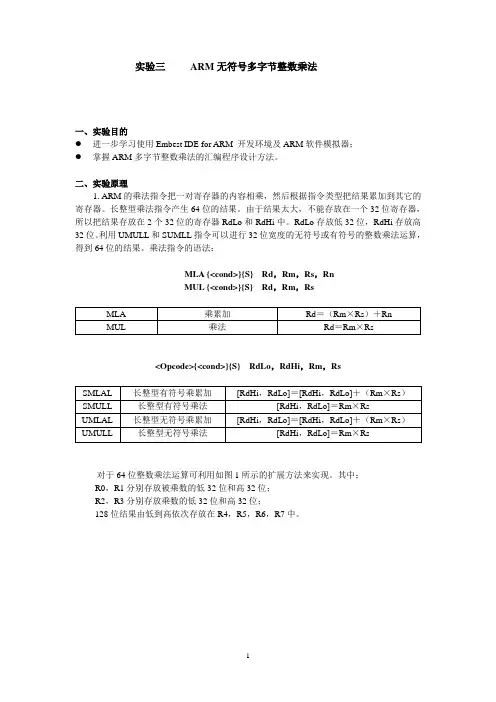
实验三ARM无符号多字节整数乘法一、实验目的●进一步学习使用Embest IDE for ARM 开发环境及ARM软件模拟器；●掌握ARM多字节整数乘法的汇编程序设计方法。
二、实验原理1. ARM的乘法指令把一对寄存器的内容相乘，然后根据指令类型把结果累加到其它的寄存器。
长整型乘法指令产生64位的结果。
由于结果太大，不能存放在一个32位寄存器，所以把结果存放在2个32位的寄存器RdLo和RdHi中。
RdLo存放低32位，RdHi存放高32位。
利用UMULL和SUMLL指令可以进行32位宽度的无符号或有符号的整数乘法运算，得到64位的结果。
乘法指令的语法：MLA {<cond>}{S} Rd，Rm，Rs，RnMUL {<cond>}{S} Rd，Rm，Rs<Opcode>{<cond>}{S} RdLo，RdHi，Rm，Rs对于64位整数乘法运算可利用如图1所示的扩展方法来实现。
其中：R0，R1分别存放被乘数的低32位和高32位；R2，R3分别存放乘数的低32位和高32位；128位结果由低到高依次存放在R4，R5，R6，R7中。
三、实验内容● 依据图2-1框图所示方法编制2个64位无符号整数乘法的程序。
● 运行Embest IDE 集成开发环境，输入自己设计的64位整数乘法汇编程序，生成目标代码，连接下载后进行调试。
四、实验步骤1. 打开memory 窗口，观察地址0x8000周围的内容。
2. 执行程序并观察和记录寄存器与memory 的值变化。
3. 结合实验内容和相关资料，观察程序运行，检验程序执行过程和结果是否正确，通过实验加深理解ARM 指令的使用。
五、实验参考程序.global _start .text _start:ldr r0, =0x12345678 ldr r1, =0x10000000 ldr r2, =0x12345678 ldr r3, =0xF000000F umull r5, r6, r2, r0 umull r7, r8, r3, r0 adds r6, r6, r7 adc r7, r8, #0x0umull r8, r9, r2, r1×＋图1： 2个64位无符号整数乘法的扩展方法LH LH H H LLumull r10, r11, r3, r1adds r9, r9, r10adc r10, r11, #0x0adds r6, r6, r8adcs r7, r7, r9adc r8, r10, #0x0stop:B stop.end六、思考题考虑利用UMLAL指令（长整型乘累加）完成上述程序功能。
第 44卷第 1期复旦学报 (自然科学版 V o1. 44, N o. 12005年 2月 Journal of Fudan University (Natural Science Feb. , 2005文章编号 :042727104(2005 0120085205Ξ双字节 Booth 乘法器的优化设计朱一杰 , 张曦 , 俞军(复旦大学专用集成电路与系统国家重点实验室 , 上海 200433 摘要 :在分析改进 Booth 算法双字节 (16bit 乘法器的基础上 , 提出一种并行的乘法器结构 , 并且在最后的快速进位链中运用了新的设计 , 提高了乘法器的速度 , 相对于传统的结构减少了一位全加器的数量 , 达到减小电路规模和芯片面积 , 降低乘法器功耗的目的 .关键词 :专用集成电路 ; 改进 Booth 算法 ; 进位保留加法器 ; 阵列操作 ; 并行乘法器中图分类号 :T N 403文献标识码 :A在数字信号处理中 , 2法 , 即通过连续地进行加法和移位来实现 . , 则 ×2个乘法器的时钟周期才能给出 2N 位乘积 , [1].2, .这 2. 前者的 N ×N 乘法器需 N 个加法器和 , N ×N 乘法器需 N 2个加法器和 N 2个部分积的与门 .为了进一步提高运算速度 , 通常采用下面 2种方法改进 :①用斜向进位代替横向进位 , 加速部分积的相加 , 即采用 Carry 2Save Adder (以下简称 CS A ; ②根据乘数中 0/1结构的特征 , 对于成串的“ 1” , 利用 2i +k -1+2i +k -2+… +2i =2i +k -2i , 减少部分积的数目 .在第 2种方法中 , 根据移位位数可将此类算法分为两类 :变长位数移位方式和固定位数移位方式 . 通过变长位数移位进行的乘法充分考虑了乘数中不同长度的“ 1” 串 , 但这必然使算法的速度强烈依赖于乘数中 0/1的结构 , 因此难以进行统一时序控制和阵列化设计 . 固定位数移位方式克服了这些缺点 , 因而获得了广泛的运用 , 特别是改进 Booth 算法 [2]很受欢迎 .在经典 Booth 算法中 , 每次检验 2位 , 完成 N 位乘法需 N 次移位和平均 N /2次加法 ; 在改进 Booth 算法中 , 每次检验 3位 , 完成 N 位乘法需 N /2次移位和平均N /2次加法 [3].表 1列举了改进 Booth 算法的编码规则 , 其中 y i +1与 y i 为考察位 , y i -1为附加考察位 , PP i 为产生的部分积 . 虽然有 8种组合 , 但真正进行的运算只有 3种 :+0, +X , +2X , 负项通过补码运算变成加法 .为了提高乘法器的速度 , 部分积的相加均采用 CS A 来实现 , 一种实用的 8位乘法器的加法阵列结构如图 1所示 . 图中的小框为基本阵列单元 1bit 全加器 , 框中标识的变量就是全加器的输入 , 如果没有标识 , 说明本全加器除了连线输入外 , 其他输入均为 0. 最后一次输出终值的加法不采用 CS A , 而是采用了带超前进位链的高速加法器 [4]. 当乘数和被乘数变为双字节 (16bit 后 , 加法阵列结构在位数上和层次上也随之增大 . 所需的 CS A 单元总数将达到 173之多 , 而且串行运算的级数也增大到 7级 CS A 加上一级高速加法器 . 这样的结构无论在面积和速度上都是不理想的 . 本文提出用并行结构代替串行结构来提高电路的整体性能 .Ξ收稿日期 :2004203222作者简介 :朱一杰 (1978— , 男 , 硕士 ; 通讯联系人俞军 .表 1改进 Booth 算法规则T ab. 1 M odified Booth Alg orithm y i +1y i y i -1PP i 000+0001+X 010+X 011+2X 100-2X 101-X 110-X 111-图 1 8位乘法器中的加法阵列结构Fig. 1 CS A architecture of 82bit multiplier1并行 Booth 乘法器在改进 Booth 算法中 , 每一次检验 3位 , , . 所以对于 16位的乘法一共需要检验8次 , 1个检验解码器的话 , 那么这 8. 如果同时使用 2, , 这也就是并行结构的雏形[5].CS A 单元 . 每次检验解码结果真正有效的数据实际上只有 16位 , 由于存在最低位的位差 , 要将低位的检验解码结果进行符号位扩展 . 检验位的位差越大 , 所需进行的符号位扩展也越大 . 所以将高 8位的检验解码结果和低 8位的检验解码结果分别累加 , 这样所用加法阵列的规模应该是最小的.图 2加法阵列Fig. 2 CS A Architecture还有一点需要考虑就是补码的校正位 Y , 如图 1中的 Y 1、 Y 3等 . 当检验解码结果是 0、 +X 或 +2X 时 , Y 取 0; 当检验解码结果是 -X 和 -2X 时 , 结果取反且Y 取 1. 如图 1所示 , 每次检验解码后所需加的校正位都和下一次的检验解码结果放在同一行加法器中累加 , 所以最后会有一行加法器只用来累加最后一次检验解码中的校正位 . 在并行结构中 , 两边分别累加 , 两边也各有一行加法器只用来累加最后的校正 68复旦学报 (自然科学版第 44卷位 . 不过由于两边最后的校正位不在同一位 , 所以可以把两行并成一行 , 以减少 CS A 单元的数量 .基于上述讨论 , 本文设计的并行结构如下 .①将高 8位的检验解码结果和低 8位的检验解码结果分别累加 .②两边的第 1、第 2行加法阵列和图 1相似 , 只是高 8位的加法阵列中最低位是 bit15.③在设计第 3行加法阵列时两边有所不同 . 高 8位处使用快速进位链加法器得出临时结果 ; 低 8位处再用一行加法器将 2个校正位加上 .④然后将高 8位的临时结果累加入低 8位 , 最后用快速进位链加法器得出最终的结果 .图 2(a 中 E ,F , G 和 H 为高 8位的检验解码结果 ,T 23— T 0为临时结果 , 将累加到低 8位的加法阵列中 . 第 1行中 E16(E 的符号位扩展 , 下同共 8位 ,F16共 6位 ,G 16共 4位 ; 第 2行中 H16共 2位 , 且最低位不需要 CS A 单元 , 所以共需 47个 CS A 单元 .图 2(b 中 A 、 B 、 C 和 D 为低 8位的检验解码结果 ,T 23— T 0为高 8位中得到的临时结果 . 第 1行中 A16共 16位 ,B16共 14位 ,C16共 12位 ; 第 2行中 D16共10位 , 最低位不需要 CS A 单元 ; 第 3行中 Y 15是最高检验解码中的校正位 , 在bit14处 ,Y 7是乘数第 7、 8位检验解码中的校正位 , 在 bit6处 , 且最低 2位不需要CS A 单元 ; 第 4行中 24个 CS A 单元用于累加临时结果 T. 所以共需 117个 CS A 单元 .将图 2(a 与 (b 合并就得到并行结构的双字节 Booth 乘法器 . 该乘法器一共需要CS A 单元 , 运算一次所需级数为 4级 CS A 加上 1级高速加法器 .无论是串行结构还是并行结构 , 在 Booth , 号位扩展 , . . 对于任意一个有符号数 SXXX , S , , 可以将其改写为 :=1111 S XXX +1, 1能预先加好 , 形成一个补偿向量 . 乘法器的字节越长 , 采用此方法所能节省的计算时间和硬件资源就越少 .如果在加法阵列中每一行之间加入寄存器 , 那么就能形成一个流水线型的Booth 乘法器 , 进一步加快速度 . 设计低 8位加法阵列时 , 先加 2位校正位 , 再加高8位的临时结果 , 以配合高 8位加法阵列的时序 . 当然 , 这样做也是有代价的 , 即所需的解码和控制电路将会比较复杂 [6], 这里就不作详细论述了 . 2快速进位链的设计在加法阵列的最后一行需要得出最终的结果 , 而不像前面行那样可以将和与进位一起传给下一行 . 如果使用串连的进位链 , 那么 N 位的加法就需要 N 个全加器的延迟时间之和 . 如果使用超前进位链又使用了太多的面积 [7].很多文献都对上面介绍的 2种进位链有详细的描述 , 可以发现这 2种进位链有一个共同点 , 就是所有的计算都是从最低位开始往高位计算 . 那么能否从最低位和最高位两端同时开始计算 , 最后在中间某一位连接上以节省时间呢 ?将图 2(b 中的 6位快速加法器展开如图 3(见第 88页 . 从图中可以看出 , 每 1位都有 2个输入端 , 而这一位的进位不仅与这 2个输入端有关 , 而且还与低一位的进位有关 . 但是如果这 2位输入都是 0或都是 1的话 , 进位就与低一位的进位没有关系了 . 利用这一原理将这 2位的输入分成 3种情况 , 如表 2(见第 88页 .(说明位的状态有 3种 , u 表示不确定 , r 表示本位保持输入之和 , i 表示本位为输入之和的非表 2中的第 1列为该位当前的判定结果 , 第 2例为比该位低的某位的 2个或者3个输入之和 . 如果一位已经被它低的某位输入判定为 r 或者 i , 那么就无需由更低的位输入判断了 , 所以表中没有列出 . 表中的第 3,4列为由输入判定的结果 , 以该位是否为最低位分成 2例 , 其中的差别就是输入的个数和在输入端为 1时的判定结果 . 这里的最低位就是指算法中两头运算在中间接连的那一位 . 如果是最低位 , 则有 3个 (多出 1个次低位的进位 , 当输入为 1时 , 最终的判定结果为 r .78第 1期朱一杰等 :双字节 Booth 乘法器的优化设计表 2进位预先判断规则表T ab. 2 Prejudging rule of carry 位的初状态低位输入中间位最低位 D[k ]=u 0D[k +1]=r D[k +1]=r D[k ]=u 1D[k +1]=u D[k +1]=r D[k ]=u 2D[k +1]=i D[k +1]=i图 3 6位高速加法器Fig. 3 62bit high 2speed adder以图 3中的 6位高速加法器为例 . 输出端的起初状态都为 u . C out 的状态先由bit5的输入 M5和 N5判断 , 如果判定结果仍为 u , 则与 P5一起再由 bit4的输入 M4和 N4判断 , 依次类推 . 当判断完最低位 (中间位后 , 所有位的状态都已确定 , 然后根据本位的状态与输入之和得出最终的结果 . 至于中间位的选择 . 就显得相当灵活 , 可以根据工艺条件选定 , 使得两边所需的逻辑运算时间大致相等即可 .3实际验证对本文设计的双字节并行 Booth (其中加法器为 6位 , 改进进位链的中间位取为 bit3 . , DC , . 可以看出 , 并行结构无论在面积 (S 、门数和时延 (t芯片面积、降低功耗的目的 ; , 而超前进位链在面积上是最大的 , 10%左右 , 达到了预期效果 .表T ab. 3 C on of parallel and serial architecture 结构类型S /μm 2门数 t dmax /ns 并行结构 905445526. 34串行结构 1075216488. 84表 4各种进位链的验比较T ab. 4 C om paris on of each kinds of Carry 2chain 进位链类型S /μm 2t dmax /ns 串行进位链 2816. 62. 36超前进位链 5103. 41. 67改进进位链 4596. 41. 67本文介绍了改进 Booth 算法及 8位乘法器的结构 , 并指出了这种结构在实现 16位乘法器中暴露出来的弊端 . 提出了一种用并行结构设计的改进 Booth 乘法器结构 . 该并行结构将运算级数由原来的 7级 CS A 加上 1级高速加法器改进为现在的4级 CS A 加上 1级高速加法器 , 提高了运算速度 . 在规模上 , 所需 CS A 单元个数由原来的 173减少至 164, 达到了减小电路规模和芯片面积 , 降低乘法器功耗的目的 . 另外还提出了一种新的快速进位链算法 , 这种算法在控制电路规模的基础上加快了运算速度 , 并且可以通过调节中间位来达到最佳效果 .参考文献 :[1]李伟华 . V LSI 设计基础 [M].北京 :电子工业出版社 ,2002.[2]韩雁 . 专用集成电路设计技术基础 [M].成都 :电子科技大学出版社 ,2000.[3] E fstathiou C , Verg os H T ,Nikolos D. M odified booth m odulo 2n21multipliers [J].Computer s , IEEE Transactions on , 2004, 53(3 :3702374.[4]沈绪榜 . 超大规模集成系统设计 [M].北京 :科学出版社 ,1991.[5] C ooper A R. Parallel architecture m odified Booth multiplier [J].Circuits , Devices and Systems , IEEE Proceedings G, 1988, 135(3 :1252128.[6] Rao V M ,N owrouzian B. A novel approach to the design and hardware im plementation of high 2speed digit 2serial m odi 2 fied 2Booth digital multipliers [J].Circuits and Systems ,1997, 3:1952219551.88复旦学报 (自然科学版第 44卷[7]谢永瑞 . V LSI 概论 [M].北京 :清华大学出版社 ,2002. Architecture Optimization of Word 2length Booth MultiplierZHU Y i 2jie ,Zhang X i ,Y u J un(ASIC &System State K ey Laboratory , Fudan Univer sity , Shanghai 200433, ChinaAbstract :Based on introducing m odified Booth alg orithm and its realization in w ord 2length multiply ,a novel parallel multiplier architecture is developed , and a new architecture is als o used in high 2speed adder. These im provements accelerate the whole multiplier and decrease the number of carry 2save adders.K eyw ords :ASIC ; m odified Booth alg orithm ; carry 2save adder ; array processing ; parallel multiplier (上接第 79页[4] Proakis J G. Digital C ommunications ,4th Ed [M].New :2[5] Ed forsO ,Sandell M ,Wils on S K, et position [J].IEEE TransCommun (7 A N e w Adaptive Modulation Algorithmfor OFDM SystemCHEN Hao 2min , X U Qiao 2yong , WAN G Z ong 2xin(Department o f Communication Science and Engineering , Fudan Univer sity , Shanghai 200433, ChinaAbstract :A new adaptive m odulation alg orithm for OFDM system id proposed. The alg orithm adopts adaptive bit loading and power allocation while maintaining constant throughput. C om pared with fixed m odulation scheme ,this alg orithm can greatly im 2prove the Bit Error Rate per formance and system throughput. This is a realizable alg orithm because of its small com putational com plexity. S imulation results show that subcarrier grouping just has a little in fluence on system per formance. Meanwhile the im per fect channel estimation has little effects on the present alg orithm.K eyw ords :communication technology ; OFDM; adaptive m odulation ; throughput 98第 1期朱一杰等 :双字节 Booth乘法器的优化设计。
