单纯形算法一般原理
- 格式:doc
- 大小:265.50 KB
- 文档页数:5

单纯形法原理单纯形法,求解线性规划问题的通用方法。
单纯形是美国数学家G.B.丹齐克于1947年首先提出来的。
它的理论根据是:线性规划问题的可行域是n维向量空间Rn中的多面凸集,其最优值如果存在必在该凸集的某顶点处达到。
顶点所对应的可行解称为基本可行解。
单纯形法的基本思想是:先找出一个基本可行解,对它进行鉴别,看是否是最优解;若不是,则按照一定法则转换到另一改进的基本可行解,再鉴别;若仍不是,则再转换,按此重复进行。
因基本可行解的个数有限,故经有限次转换必能得出问题的最优解。
如果问题无最优解也可用此法判别。
单纯形法是从某一基可行解出发,连续地寻找相邻的基可行解,直到达到最优的迭代过程,其实质是解线性方程组。
概述:根据单纯形法的原理,在线性规划问题中,决策变量(控制变量)某1,某2,…某n的值称为一个解,满足所有的约束条件的解称为可行解。
使目标函数达到最大值(或最小值)的可行解称为最优解。
这样,一个最优解能在整个由约束条件所确定的可行区域内使目标函数达到最大值(或最小值)。
求解线性规划问题的目的就是要找出最优解。
最优解可能出现下列情况之一:①存在着一个最优解;②存在着无穷多个最优解;③不存在最优解,这只在两种情况下发生,即没有可行解或各项约束条件不阻止目标函数的值无限增大(或向负的方向无限增大)。
单纯形法的一般解题步骤可归纳如下:①把线性规划问题的约束方程组表达成典范型方程组,找出基本可行解作为初始基本可行解。
②若基本可行解不存在,即约束条件有矛盾,则问题无解。
③若基本可行解存在,从初始基本可行解作为起点,根据最优性条件和可行性条件,引入非基变量取代某一基变量,找出目标函数值更优的另一基本可行解。
④按步骤3进行迭代,直到对应检验数满足最优性条件(这时目标函数值不能再改善),即得到问题的最优解。
⑤若迭代过程中发现问题的目标函数值无界,则终止迭代。
用单纯形法求解线性规划问题所需的迭代次数主要取决于约束条件的个数。
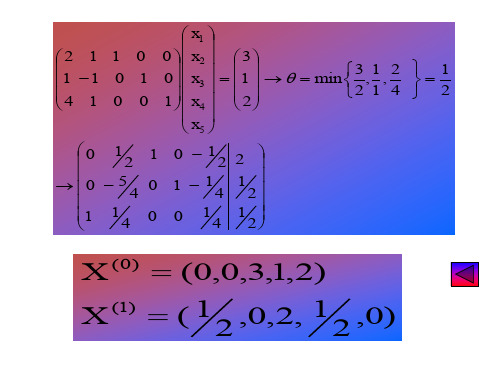




运筹学单纯形法的迭代原理讲解
单纯形法是一种用于解决线性规划问题的常用方法,其基本思想是通过迭代的方式逐步接近最优解。
下面是单纯形法的迭代原理的讲解:
1. 初始解的选择:首先需要选择一个初始解,通常选择的方法是构造一个基可行解,即使所有的约束条件都满足的解。
2. 判断最优性:在每一次迭代中,需要判断当前解是否为最优解。
首先,计算当前解对应的目标函数值。
然后,检查是否存在非基变量的系数大于等于0(对于最小化问题)或者小于等于0(对于最大化问题),如果存在这样的非基变量,则当前解不是最优解;如果不存在这样的非基变量,则当前解是最优解。
3. 生成新解:如果当前解不是最优解,则需要生成新的解。
首先,选择一个非基变量,使得目标函数的值可以通过增加(对于最小化问题)或减少(对于最大化问题)该变量的值来改善。
然后,需要计算这个非基变量能够增加或减少的最大量,称为变量的进步长度。
最后,通过调整基变量的值来生成新的解。
4. 更新目标函数和约束条件:在生成新解之后,需要更新目标函数和约束条件,以便于下一次迭代。
具体操作包括计算新解对应的目标函数值,计算新解对应的约束条件的值,调整目标函数和约束条件的系数。
5. 重复迭代:根据判断最优性的结果,进行下一次迭代。
如果当前解是最优解,
则算法结束;否则,继续进行下一次迭代。
通过不断重复这一迭代过程,直到找到最优解或者确定问题无解为止。
单纯形法的迭代过程一般会在有限次数内结束,并且能够得到最优解。
单纯形法原理单纯形法是一种用于求解线性规划问题的数学方法,它通过不断地移动可行解,逐步接近最优解。
单纯形法的基本思想是从一个基本可行解出发,通过有限次迭代,逐步向着最优解靠近。
这种方法的优点是能够有效地处理大规模的线性规划问题,并且在实际应用中取得了很好的效果。
单纯形法的原理可以通过以下步骤来进行解释:首先,我们需要将线性规划问题转化为标准形式,即将不等式约束转化为等式约束,并引入松弛变量。
这样,原始的线性规划问题就可以表示为一个矩阵形式Ax=b的形式,其中A是一个m×n的矩阵,x是一个n维向量,b是一个m维向量。
接下来,我们需要找到一个初始的基本可行解。
这个基本可行解对应于一个m×m的单位矩阵Im,以及一个n维的零向量。
我们可以通过将单位矩阵对应的列向量代入原始的线性规划问题中,来求解初始的基本可行解。
然后,我们需要计算出一个非基本变量的非负进入向量。
这个向量对应于目标函数的系数向量与A的转置矩阵的乘积。
通过计算这个进入向量,我们可以确定哪一个非基本变量可以进入基本变量集合,从而使得目标函数值增加。
接着,我们需要计算出一个基本变量的非正离开向量。
这个向量对应于基本变量对应的列向量与A的转置矩阵的乘积。
通过计算这个离开向量,我们可以确定哪一个基本变量可以离开基本变量集合,从而使得目标函数值继续增加。
最后,我们需要进行基本变量与非基本变量的交换,并更新基本可行解。
这个过程可以通过一系列的矩阵运算来实现,从而得到一个新的基本可行解。
然后,我们可以继续重复上述步骤,直到找到最优解为止。
通过上述步骤,我们可以看出单纯形法的原理是通过不断地移动可行解,逐步接近最优解。
这种方法的优点是能够有效地处理大规模的线性规划问题,并且在实际应用中取得了很好的效果。
总之,单纯形法是一种用于求解线性规划问题的有效方法,它的原理是通过不断地移动可行解,逐步接近最优解。
在实际应用中,单纯形法已经取得了很好的效果,能够有效地处理大规模的线性规划问题。
单纯形算法的一般原理
单纯形法的基本思路是有选择地取基本可行解,即是从可行域的一个极点出发,沿着可行域的边界移到另一个相邻的极点,要求新极点的目标函数值不比原目标函数值差。
考虑到如下线性规划问题:
其中A一个m ×n 矩阵,且秩为m ,b总可以被调整为一个m 维非负列向量,C为n 维行向量,X为n 维列向量。
根据线性规划基本定理:
如果可行域D={ X∈Rn / AX=b,X≥0}非空有界,
则D上的最优目标函数值Z=CX一定可以在D的一个顶点上达到。
这个重要的定理启发了Dantzig 的单纯形法,
即将寻优的目标集中在D 的各个顶点上。
Dantzig 的单纯形法把寻优的目标集中在所有基本可行解
(即可行域顶点)中。
其基本思路是从一个初始的基本可行解出发,寻找一条达到 最优基本可行解的最佳途径。
单纯形法的一般步骤如下:
(1)寻找一个初始的基本可行解。
(2)检查现行的基本可行解是否最优,如果为最优,
则停止迭代,已找到最优解,否则转一步。
(3)移至目标函数值有所改善的另一个基本可行解,
然后转会到步骤(2)。
求解思想如下图所示:
maxZ=CX AX=b X 0⎧⎨≥⎩
确定初始的基本可行解等价于确定初始的可行基,一旦初始的可行基确定了,那么对应的初始基本可行解也就唯一确定
为了讨论方便,不妨假设在标准型线性规划中,系数矩阵A中前m 个系数列向量恰好构成一个可行基,即
A=(BN),其中
B=(P1,P2,…Pm )为基变量x1,x2,…xm 的系数列向量 构成的可行基,
N=(Pm+1,Pm+2, …Pn)为非基变量xm+1,xm+2, …xn 的 系数列向量构成的矩阵。
那么约束方程AX=b 就可表示为:
用可行基B的逆阵B-1左乘等式两端,再通过移项可推得:
若令所有非基变量 ,则基变量
由此可得初始的基本可行解
B B N N X AX=(BN)=BX +NX =b X ⎛⎫ ⎪⎝⎭-1-1B N X =B b-B NX N X =0-1B X =B b 1B b X=0-⎛⎫ ⎪⎝⎭-1-1-1B N B N N B AX=b BX +NX =b X =B b-B NX X =0,X =B b →→→
● 问题:
➢ 要判断m 个系数列向量是否恰好构成一个基并不是一件容易的事。
基由系数矩阵A中m 个线性无关的系数列向量构成。
但是要判断m 个系数列向量是否线性无关并非易事。
➢ 即使系数矩阵A中找到了一个基B ,也不能保证该基恰好是可行基。
因为不能保证基变量XB=B-1b ≥0。
➢ 为了求得基本可行解 ,必须求基B的逆阵B-1。
但是求逆阵B-1也是一件麻烦的事。
● 结论:在线性规划标准化过程中设法得到一个m 阶单位矩阵I 作为初始可行基B,
为了设法得到一个m 阶单位矩阵I 作为初始可行基B,可在性规
划标准化过程中作如下处理:
➢ 若在化标准形式前,m 个约束方程都是“≤”的形式,
那么在化标准形时只需在一个约束不等式左端都加上一个松弛变
量xn+i (i=12…m)。
➢ 若在化标准形式前,约束方程中有“≥”不等式,
那么在化标准形时除了在方程式左端减去剩余变量使不等式变
成等式以外,还必须在左端再加上一个非负新变量,称为
人工变量.
➢ 若在化标准形式前,约束方程中有等式方程,那么可以直接在
等式左端添加人工变量。
加入已求的一个基本可行解 , ,将这一基本可行解代入目标函数,可
求得相应的目标函数值
其中 ,
分别表示基变量和非基变量所对应的价值系数子向量。
要判定 是否已经达到最大值,只需将 代入目标
函数,使目标函数用非基变量表示,即:
1B b X=0-⎛⎫ ⎪⎝⎭1B b X=0-⎛⎫ ⎪⎝⎭1-1B N B B b Z=CX=(C C )=C B b 0-⎛⎫ ⎪⎝⎭B 12m N m+1m+2n C =(c ,c ,c ), C =(c ,c ,c )L L -1B Z=C B b -1-1B N X =B b-B NX B B N N -1-1B B N N B N N N -1-1B N B N X Z=CX=(C C )X =C X +C X =C (B b-B NX )+C X =C B b+(C -C B N)X ⎛⎫ ⎪⎝⎭m+1m+2-1-1B N N B m+1,m+1,n n x x C B b+σX C B b+(σσσ)x ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭
@L M
其中 称为非基变量XN 的检验向量,它的各个分量称为检验数。
若σN 的每一个检验数均小于等于0,即σN ≤0,那么现在的基本可行解就是最优解。
对于单纯形算法有如下定理:
定理1:最优解判别定理
对于线性规划问题 若某个基本可行解所对应的检验向量 , 则这个基本可行解就是最优解。
定理2:无穷多最优解判别定理
若 是一个基本可行解,所对应的检验向量
,
其中存在一个检验数σm+k=0,则线性规划问题有无穷多最优解。
如果现行的基本可行解X不是最优解,即在检验向量
中存在正的检验数,则需在原基本可行解X的基础上寻找一个新的基本可行解,并使目标函数值有所改善。
具体做法是:
➢ 先从检验数为正的非基变量中确定一个换入变量,使它从非基变量变成基变量(将它的值从零增至正值),
➢ 再从原来的基变量中确定一个换出变量,使它从基变量变成非基变量(将它的值从正值减至零)。
由此可得一个新的基本可行解,由 可知,这样的变换一定能使目标函数值有所增加。
此外,换入变量原则为最大增加原则,即:
假设检验向量 ,若其中有两个以上的检验数为正,那么为了使目标函数值增加得快些,通常要用“最大增加原则”,即选取最大正检验数所对应的非基变量为换入变量,即若
则选取对应的 为换入变量,由于
且为最大,因此当 由零增至正值,可使目标函数值
-1
N N B m+1m+1n =C -C B N=(,,)σσσσL {}n maxZ=CX,D=X R /AX=b,X
0∈≥-1N N B =C
-C B N 0σ≤m+1m+2-1B m+1,m+1,n n x x Z C B b+(σσσ)x ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭L M 1B b X=0-⎛⎫ ⎪⎝⎭-1N N B =C -C B N 0σ≤-1N N B =C -C B N σm+1m+2-1B m+1,m+1,n n x x Z C B b+(σσσ)x ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭
L M -1N N B m+1m+2
n =C -C B N=(,,)σσσσL {}j j m+k max σ/σ>0,m+1j n =σ≤≤m+k x m+k 0σ>m+k x
最大限度的增加。
换出变量的原则则为最小比值原则,即: 换出变量原则为最小比值原则 如果确定 为换入变量,方程
其中 为A中与 对应的系数列向量。
现在需在
中确定一个基变量为换出变量。
当 由零慢慢增加到某个值时, 的非负性可能被打破。
为保持解的可行性,可以按最小比值原则确定换出变量:
若
则选取对应的基变量
为换出变量。
定理3:无最优解判别定理
若 是一个基本可行解,
有一个检验数 ,但是 ,
则该线性规划问题无最优解。
证明略。
m+1m+2-1B m+1,m+1,n n x x Z C B b+(σσσ)x ⎛⎫ ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭L M m+k x -1-1-1-1B N B m+k m+k X =B b-B NX X =B b-B P x ⇒m+k P m+k x B 12m X =(x ,x ,x )T L m+k x B X -1-1-1i m+k i -1-1m+k i m+k (B b)(B b)min /(B P )>0,1i m =(B P )(B P )l l ⎧⎫⎪≤≤⎨⎬⎪⎭⎩x l 1B b X=0-⎛⎫ ⎪⎝⎭m+k 0σ>-1m+k B P 0≤。