苏科版初一数学期末复习讲义_平面图形的认识(一)1225

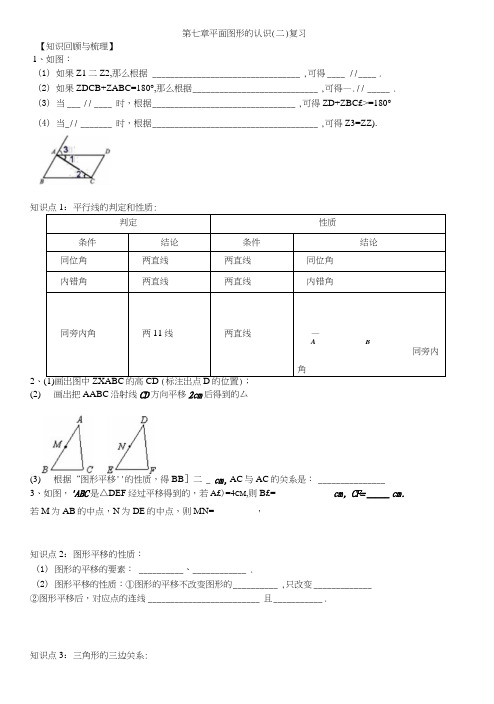
第七章平面图形的认识(二)复习【知识回顾与梳理】1、如图：(1)如果Z1二Z2,那么根据_________________________________ ,可得____ // ____ .(2)如果ZDCB+ZABC=180°,那么根据____________________________ ,可得—.// _____ .(3)当___ // ____ 时，根据________________________________ ,可得ZD+ZBC£>=180°(4)当_// _______ 时，根据_____________________________________ ,可得Z3=ZZ).知识点1：平行线的判定和性质:判定性质条件结论条件结论同位角两直线两直线同位角内错角两直线两直线内错角同旁内角两11线两直线—A B同旁内角2、(2)画出把AABC沿射线CD方向平移2cm后得到的厶(3)根据“图形平移''的性质，得BB］二 _ cm, AC与AC的关系是：_______________3、如图，'ABC是△DEF经过平移得到的，若A£)=4CM,则B£= ____________ c m, CF= _____ cm.若M为AB的中点，N为DE的中点，则MN= ________ ，知识点2：图形平移的性质：(1)图形的平移的要素： __________、____________ .(2)图形平移的性质：①图形的平移不改变图形的__________ ,只改变_____________②图形平移后，对应点的连线_________________________ 且___________ .知识点3：三角形的三边关系:练习：①长度为2cm、3cm. 4cm和5cm的木棒，从中任取3根，可搭成___________ 种不同的三角形②三角形的三边长为3, a, 7,则a的取值范围是 ______________ ；如果第三条边是偶数，则第三条边可能是___________ ;如果这个三角形中有两条边相等，那么它的周长是 _________ •知识点4：三角形的三条重要线段（1）三角形高线；（2）三角形角平分线；（3）三角形中线练习：三角形的三条高相交于一点，此一点定在（）A.三角形的内部B.三角形的外部C.三角形的一条边上D.不能确定知识点5：（1）三角形的内角和等于______ ；（2）直角三角形的两个锐角_________ ・知识点6：三角形外角的性质三角形的一个外角等于 __________________ ；知识点7：多边形内、外角和（1）/?边形内角和等于______ ;（2）〃边形从一个顶点出发的对角线条数为________ ；把多边形分成个三角形；对角线总条数为;（3）任意多边形的外角和都为• 练习:①一个多边形的内角和是540,那么这个多边形是边形；②一个多边形的内角和是外角和的4倍，那么这个多边形是 ______ 边形；③一个多边形的每个内角都等于144°,则此多边形是_________ 边形;【基础练习】1.在ZXABC 中，ZA=40°, ZB=ZC,则ZC= _________ .2.一个三角形三个内角度数的比是2 ： 3 ： 4,那么这个三角形是_三角形，它的外角比是__________ •3.在ZVIBC 中，ZA-ZB=36°, ZC=2ZB,贝iJZA=_, ZB=_, ZC=_.4.如图，DE〃BC, ZAD£=60°, ZC=50°,则ZA=_.5.十二边形的内角和是_______ 若每个外角相等，则每个外角的度数为 _________ °..6.多边形的每个内角都是每个外角的4倍，则这个多边形的边数是—.7.某同学从长度分别为5、7、9、13 （单位：厘米）的四根木棒中任意取岀三根，将它们首尾顺次相接搭成三角形.最多可摆出_______ 个不同的三角形.8.如图，AD 平分ZBAC,其中ZB=50。

苏科版数学七年级上册第六章平面图形的认识教教学设计一. 教材分析苏科版数学七年级上册第六章《平面图形的认识》主要包括了平面图形的性质和判定，以及图形的对称性、中心对称和轴对称的概念。

本章内容是学生进一步认识和理解几何图形的基础，对于培养学生的空间想象能力和逻辑思维能力具有重要意义。

二. 学情分析七年级的学生已经初步掌握了平面图形的知识，但对于一些概念和性质的深入理解还需加强。

此外，学生对于图形的直观感知能力较强，但逻辑推理和证明能力有待提高。

因此，在教学过程中，需要注重引导学生从直观到抽象的思维转变，培养他们的逻辑推理能力。

三. 教学目标1.理解平面图形的性质和判定，掌握图形的对称性、中心对称和轴对称的概念。

2.培养学生空间想象能力和逻辑思维能力，提高他们运用几何知识解决实际问题的能力。

3.培养学生合作交流、归纳总结的能力，提高他们的数学素养。

四. 教学重难点1.教学重点：平面图形的性质和判定，图形的对称性、中心对称和轴对称的概念。

2.教学难点：图形的对称性、中心对称和轴对称的判断和应用。

五. 教学方法1.采用问题驱动法，引导学生主动探究平面图形的性质和判定。

2.运用直观教学法，通过实物模型、图形软件等辅助教学，提高学生的空间想象能力。

3.采用合作交流法，鼓励学生分组讨论，培养学生的团队协作能力。

4.运用归纳总结法，引导学生自主总结平面图形的性质和判定方法。

六. 教学准备1.准备相关的教学PPT，包括平面图形的性质和判定，以及对称性的概念和判定。

2.准备实物模型、几何画板等教学辅助工具，以便进行直观教学。

3.准备一些相关的练习题，用于巩固所学知识。

七. 教学过程1.导入（5分钟）通过展示一些实际生活中的图形，如教室的黑板、衣服上的图案等，引导学生关注平面图形的对称性，激发他们的学习兴趣。

2.呈现（10分钟）利用PPT呈现平面图形的性质和判定，对称性的概念和判定。

通过讲解和示范，让学生初步理解平面图形的性质和判定方法。

平面图形的认识一、教材分析1。

本章中所涉及的平面图形，上一学段学生都已接触过，因此要注意与学生已学知识的衔接。

2.要使学生经历三角形、多边形和圆等有关概念的形成、抽象过程，把握它们的实质，初步形成几何建模的意识。

3.对于图形性质,要使学生经历实验、观察、探索、猜想、交流、发现的过程，并尝试进行合情推理或验证。

三角形是最简单，最基本的几何图形之一,在生活中随处可见,它不仅是研究其他图形的基础，而且在解决实际问题中也有着广泛的应用.探索和掌握三角形的基本性质对学生更好地认识现实世界,发展空间观念有着重要作用。

课本首先从学生熟悉的三角形开始，在感性认识的基础上，对三角形的有关概念进行定义，然后探索三角形三内角,三边之间的关系，多边形的内角和,外角和等性质,为进一步的几何学习做好准备。

在介绍三角形的有关概念，探索三角形三内角，三边之间的关系的教学中,课本力求创设丰富的现实情境,使学生经历从现实生活中抽象出几何模型和运用所学知识解决问题的过程。

在内容的呈现上,课本提供了“数学实验室”等系列活动，给学生提供充分的实践,探索，交流的空间，引导学生发现三角形的有关结论.在探索多边形的内角和与外角和公式的教学中，课本为学生创设了主动参与学习的情境,让学生通过实验,观察，猜想，归纳，领略化复杂为简单，化未知为已知的思想方法，积累数学活动经验，发展有条理的思考与表达.二、教学目标1。

经历从现实世界中抽象出平面图形的过程,认识数学与实际生活的紧密联系,感受图形世界的丰富多彩.2。

经历三角形、多边形、圆的有关概念的形成过程，培养学生的抽象概括能力. 3.经历三角形、多边形、圆的有关性质的探索过程了解三角形的三边关系、内外角关系、多边形的内角和公式，会用它们进行简单的有关计算，进一步发展学生的空间观念、合情推理意识、主动探究的习惯以及清晰、条理的语言表达能力。

4.经历多边形密铺条件的探索过程,尝试从不同角度解决问题，形成初步的创新意识。

2019-2020学年七年级上学期期末复习备考秘籍（苏教版）专题1.6平面图形的认识考点一、直线射线线段例 1.如图，如果用剪刀沿直线将一个正方形图片剪掉一部分，发现剩下部分的周长比原正方形图片的周长要小，能正确解释这一现象的数学知识是（）A．垂线段最短B．经过一点有无数条直线C．经过两点，有且仅有一条直线D．两点之间，线段最短【变式训练】1．如图，经过刨平的木板上的A，B两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）A．两点之间，线段最短B．两点确定一条直线C．垂线段最短D．在同一平面内，过一点有且只有一条直线与已知直线垂直2．如图，某同学用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长小，能正确解释这一现象的数学知识是（）A．两点之间，直线最短B．两点确定一条直线C．两点之间，线段最短D．经过一点有无数条直线3．下列说法中，正确的有（）①过两点有且只有一条直线，②连结两点的线段叫做两点的距离，③两点之间，线段最短，④AB＝BC，则点B是线段AC的中点．A．4个B．3个C．2个D．1个考点二、基本画图例2．根据语句画出图形：如图，已知A、B、C三点．①画线段AB；②画射线AC；③画直线BC；④取AB的中点P，连接PC．【变式训练】1．如图，已知四点A、B、C、D，请用尺规作图完成．（保留画图痕迹）（1）画直线AB；（2）画射线AC；（3）连接BC并延长BC到E，使得CE＝AB+BC；（4）在线段BD上取点P，使P A+PC的值最小．2．如图，C是线段AB外一点，按要求画图：（1）画射线CB；（2）反向延长线段AB；（3）连接AC，并延长AC至点D，使CD＝AC．考点三、线段的有关计算问题例3．如图，点C在线段AB上，点M、N分别是AC、BC的中点．（1）若AC＝8cm，CB＝6cm，求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB＝a，其它条件不变，你能猜想MN的长度吗？写出你的结论并说明理由；（3）若点C在线段AB的延长线上，且满足AC﹣BC＝b，M、N分别为AC、BC的中点，你能猜想MN 的长度吗？请画出图形并写出你的结论（不必说明理由）．【变式训练】1．如果A、B、C三点在同一直线上，且线段AB＝6cm，BC＝4cm，若M，N分别为AB，BC的中点，那么M，N两点之间的距离为（）A．5 cm B．1 cm C．5或1 cm D．无法确定2．如图，已知点A、B、C、D、E在同一直线上，且AC＝BD，E是线段BC的中点．（1）点E是线段AD的中点吗？说明理由；（2）当AD＝10，AB＝3时，求线段BE的长度．2．如图，点C在线段AB上，点M、N分别是AC、BC的中点．（1）若AC＝9cm，CB＝6cm，求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB＝acm，其它条件不变，你能猜想MN的长度吗？并说明理由．你能用一句简洁的话描述你发现的结论吗？（3）若C在线段AB的延长线上，且满足AC﹣BC＝bcm，M、N分别为AC、BC的中点，你能猜想MN 的长度吗？请画出图形，写出你的结论，并说明理由．考点四、角的有关认识例4．一副三角板按如图所示的方式摆放，且∠1的度数是∠2的3倍，则∠2的度数为（）A．20°B．22.5°C．25°D．67.5°【变式训练】1．如图，一副三角尺按不同的位置摆放，摆放位置中∠α＝∠β的图形有（）A．1个B．2个C．3个D．4个2．如图，一副三角尺按不同的位置摆放，摆放位置中∠α＝∠β的图形个数是（）A．1 B．2 C．3 D．4考点五、平行与垂直例5．三条直线a、b、c中，a∥b，b∥c，则直线a与直线c的关系是（）A．相交B．平行C．垂直D．不确定【变式训练】1．下列说法中，正确的是（）A．两条不相交的直线叫做平行线B．一条直线的平行线有且只有一条C．在同一平面内，若直线a∥b，a∥c，则b∥cD．若两条线段不相交，则它们互相平行2．在同一个平面内，两条直线的位置关系是（）A．平行或垂直B．相交或垂直C．平行或相交D．不能确定3．下列说法中，正确的是（）A．两条不相交的直线叫平行线B．一条直线的平行线有且只有一条C．若直线a∥b，a∥c，则b∥cD．两条直线不相交就平行考点六、角的有关计算例6．如图，O为直线AB上一点，∠AOC＝50°，OD平分∠AOC，∠DOE＝90°．（1）求出∠BOD的度数；（2）请通过计算说明OE是否平分∠BOC．【变式训练】1．如图，经测量，B处在A处的南偏西57°的方向，C处在A处的南偏东15°方向，C处在B处的北偏东82°方向，求∠C的度数．2．如图，已知∠BOC＝2∠AOC，OD平分∠AOB，且∠COD＝20°，求∠AOB的度数．3．已知如图，直线AB、CD相交于点O，∠COE＝90°．（1）若∠AOC＝36°，求∠BOE的度数；（2）若∠BOD：∠BOC＝1：5，求∠AOE的度数；（3）在（2）的条件下，过点O作OF⊥AB，请直接写出∠EOF的度数．4．若一个角的补角是这个角的余角的3倍，求这个角的度数．1．如图，C，D是线段AB上两点，若CB＝4cm，DB＝7cm，且D是AC的中点，则AC的长等于（）A．3 cm B．6 cm C．11 cm D．14 cm2．已知点C在线段AB上，则下列条件中，不能确定点C是线段AB中点的是（）A．AC＝BC B．AB＝2AC C．AC+BC＝AB D．3．如图，C、D是线段AB上两点，若BC＝3cm，BD＝5cm，且D是AC的中点，则AC的长为（）A．2cm B．4cm C．8cm D．13cm4．如图所示，线段AB＝10，M为线段AB的中点，C为线段MB的中点，N为线段AM的一点，且MN＝1，线段NC的长（）A．2 B．2.5 C．3 D．3.55．已知在同一平面内，有三条直线a，b，c，若a∥b，b∥c，则直线a与直线c之间的位置关系是（）A．相交B．平行C．垂直D．平行或相交6．在同一平面内，不重合的两条直线的位置关系可能是（）A．相交或平行B．相交或垂直C．平行或垂直D．不能确定7．下面的四个图形中，∠1与∠2是对顶角的是（）A．B．C．D．8．已用点A、B、C、D、E的位置如图所示，下列结论中正确的是（）A．∠AOB＝130°B．∠AOB＝∠DOEC．∠DOC与∠BOE互补D．∠AOB与∠COD互余9．如图，点C是线段AB上的点，点D是线段BC的中点，若AB＝10，AC＝6，求CD的长．10．几何计算：如图，已知∠AOB＝40°，∠BOC＝3∠AOB，OD平分∠AOC，求∠COD的度数．解：因为∠BOC＝3∠AOB，∠AOB＝40°所以∠BOC＝°所以∠AOC＝+＝°+°＝°因为OD平分∠AOC所以∠COD=12＝°．11．如图，∠AOB＝∠COD＝90°，OC平分∠AOB，∠BOD＝3∠DOE．试求∠COE的度数．12．把一副三角板的直角顶点O重叠在一起．（1）如图（1），当OB平分∠COD时，则∠AOD与∠BOC的和是多少度？（2）如图（2），当OB不平分∠COD时，则∠AOD和∠BOC的和是多少度？（3）当∠BOC的余角的4倍等于∠AOD，则∠BOC多少度？13．如图，直线AB、CD相交于点O，过点O作两条射线OM、ON，且∠AOM＝∠CON＝90°①若OC平分∠AOM，求∠AOD的度数．②若∠1∠BOC，求∠AOC和∠MOD．。

EDC BA 初一（上）数学学科教案（0712）课题：平面图形的认识（二）（1） 课型：复习课上课时间： 班级： 教师： 教学目标：1．复习巩固平行线的判定和性质.2．会灵活运用平行线的判定和性质解决问题. 3．体会和感受“数形结合”和“分类”的思想.教学重点：熟练运用平行线的判定和性质解决问题. 教学难点：从复杂图形中分解出基本图形． 教学过程： 【复习回顾】1、“三线八角”① 如何由线找角：一找线，二看型。

同位角是“F”型； 内错角是“Z”型； 同旁内角是“C ”型。

② 如何由角找线：组成角的三条线中的公共直线就是截线。

练习1.将一直角三角板与两边平行的纸条如图所示放置，下列结论： （1）∠1＝∠2；（2）∠3＝∠4；（3）∠2＋∠4＝90°；（4）∠4＋∠5＝180°，其中正确的是__________.2、平行公理：如果两条直线都和第三条直线平行，那么这两条直线也平行。

简述：平行于同一条直线的两条直线平行。

练习2：如图，AB ∥CD ，若∠ABE ＝120°，∠DCE ＝35°，求∠BEC ．3、平行线的判定和性质：判定定理性质定理条件 结论 条件 结论 同位角相等 两直线平行 两直线平行 同位角相等 内错角相等 两直线平行 两直线平行 内错角相等 同旁内角互补两直线平行两直线平行同旁内角互补 练习3.如图，已知∠1＝∠2，∠B ＝∠C ． 证明：（1）CE ∥BF ；（2）∠B ＝∠3．AEDFC 3 1 2 12 345ED CB A4、图形平移：（1）平移两要素：方向、距离。

（2）性质：对应点连线互相平行（或在同一直线上）且相等；对应线段互相平行（或在同一直线上）且相等； 对应角相等。

练习4.如图，△ABC 中，AB ＝5cm, ∠ACB ＝40°,现将其 沿AD 方向平移6cm 得到△DEF ．(1)图中可知道长度的线段有__________________________；(2)图中互相平行的线段有____________________________；(3)若∠CBE ＝60°，则∠ACF 的度数是__________.练习5.如图，将网格中的△ABC 向右平移3格，再向上平移2格之 后得到△A 1B 1C 1，若△ABC 的顶点的位置分别用一对数表示： A （1，1）、B （4，2）、C （3，3），你能理解这一对数所表达的信息吗？请你根据你得到的信息表示出A 1，B 1，C 1的位置．【复习研讨】例1.已知三条不同的直线a ，b ，c 在同一平面内，下列四个结论中，正确的是 ．①如果a ∥b ，a ⊥c ，那么b ⊥c ; ②如果b ∥a ，c ∥a ，那么b ∥c ； ③如果b ⊥a ，c ⊥a ，那么b ⊥c ； ④如果b ⊥a ，c ⊥a ，那么b ∥c ．例2.如图，已知AB ∥CD ，BE 平分∠ABC ，DE 平分∠ADC ，∠BAD ＝50°. （1）求∠EDC 的度数；（2）若∠BCD ＝n °,求∠BED 的度数.【拓展提升】例3.如图所示，△ABC 中，AD ⊥BC ，AE 平分∠BAC ． （1）若∠B =30°，∠C =70°，求∠DAE 的度数；（2）△ABC 中，若∠B =α，∠C =β（α＜β），请你根据（1）的结果 猜想∠DAE 与α，β间的等量关系，并说明理由．D F A C EB C B A例4.已知如图，射线CB ∥OA ，∠C ＝∠OAB ＝100 ,E 、F 在CB 上，且满足∠FOB ＝∠AOB ，OE 平分∠COF . ⑴求∠EOB 的度数； ⑵若平行移动AB ，那么∠OBC ：∠OFC 的值是否随之变化？若变化，找出变化规律；若不变，求出这个比值；⑶在平行移动AB 的过程中，是否存在某种情况，使∠OEC ＝∠OBA ？例5.如图（1），△ABC 是一个三角形的纸片，点D 、E 分别是△ABC 边上的两点，将∠A 沿DE 折叠后，点A 的对应点记为A ’.（1）若点A’落在AC 边上，则∠BDA′与∠A 的关系是_____________．（2）：如果折成图2的形状，猜想∠BDA′、∠CEA ′和∠A 的关系，并说明理由． （3）：如果折成图3的形状，猜想∠BDA ′、∠CEA′和∠A 的关系，并说明理由．【课堂小结】 【教学反思】CB A A ′DE图2A A ′B EDC图1AA ′B EDC图3。