反应谱理论
- 格式:ppt
- 大小:350.00 KB
- 文档页数:33


抗震结构设计谱理论一、绪论1.1 抗震结构设计谱的背景反应谱理论是描述地震工程和抗震设计中结构体系激励和响应关系的重要工具。
由于反应谱可以直接给出地震动作用下单自由度体系的最大反应,因而成为结构动力分析和抗震设计中关注的焦点。
抗震设计谱是以地震动记录资料为依据,经统计分析和平滑化处理,结合当前经济发展水平和要求的基础上确定的。
然而,由于地震动的复杂性以及对反应谱规律认识的不足,使得抗震规范设计谱往往不能全面准确地反映地震动的客观特征,这也就不可避免地影响到其使用范围和结构的抗震安全。
另外,设计谱的传统建立方法对已获取大量地震动记录的国家和地区是来说是可行的,但对缺少地震动记录的地区来说如何确定设计谱也是值得探讨的。
因此,揭示地震动的普遍规律和新特征,解决这一领域面临的诸多问题依然是地震工程界的重要课题。
1.2 反应谱概念与研究意义抗震设计中采用的地震动参数习惯上称为设计地震,尽管工程界早已习惯于选择地震动的幅值、频谱和持时三要素作为工程地震动参数,但由于反应谱不能有效地反映持时的影响,因此,世界上绝大多数国家的抗震设计规范选择幅值和频谱作为设计参数。
通常使用的地震动参数包括峰值加速度(或有效峰值加速度)和规准设计谱。
因此,设计地震主要归结为设计谱的研究。
在输入的地震动加速度时程给定后,以阻尼常数作为参数时,单自由度体系的最大相对位移反应、最大相对速度反应和最大绝对加速度反应,针对无阻尼固有周期画成的图形,分别称为相对位移反应谱、相对速度反应谱和绝对加速度反应谱,总称为地震反应谱。
或者简称为位移反应谱、速度反应谱和加速度反应谱,总称为反应谱。
设计反应谱的演变是一个随着震害经验和强震记录的积累以及对地震动反应谱特性的不断认识而逐渐深入的过程,无论是考虑场地条件,还是考虑近远震的影响,从实质上讲,设计反应谱的演变都是朝着场地地震环境相关性设计反应谱的方向发展,而场地地震环境的区别主要表现在场地特征周期和反应谱谱值上,我国《地震动参数区划图》也将反应谱的特征周期和地震动加速度作为反应谱的两个独立的参数,因此,设计反应谱的演变主要体现在对反应谱的特征周期以及反应谱谱值的不断修正上。

抗震设计中反应谱的应用一.什么就是反应谱理论在房屋工程抗震研究中,反应谱就是重要的计算由结构动力特性所产生共振效应的方法。
它的书面定义就是“在给定的地震加速度作用期间内,单质点体系的最大位移反应、速度反应与加速度反应随质点自振周期变化的曲线。
用作计算在地震作用下结构的内力与变形”,反应谱理论考虑了结构动力特性与地震动特性之间的动力关系,通过反应谱来计算由结构动力特性(自振周期、振型与阻尼)所产生的共振效应,但其计算公式仍保留了早期静力理论的形式。
地震时结构所受的最大水平基底剪力,即总水平地震作用为:FEK = kβ(T)G式中,k为地震系数,β(T)则就是加速度反应谱Sa(T)与地震动最大加速度a的比值,它表示地震时结构振动加速度的放大倍数。
β(T)=Sa(T)/a反应谱理论建立在以下基本假定的基础上:1)结构的地震反应就是线弹性的,可以采用叠加原理进行振型组合;2)结构物所有支承处的地震动完全相同:3)结构物最不利地震反应为其最大地震反应:4)地震动的过程就是平稳随机过程。
二.实际房屋抗震设计中的应用为了进行建筑结构的抗震设计,必须首先求得地震作用下建筑结构各构件的内力。
一般而言,求解建筑结构在地震作用下构件内力的方法主要有两种,一种就是建立比较精确的动力学模型进行动力时程分析计算,这种方法比较费时费力,其精确度取决于动力学模型的准确性与所选取地震波就是否适当,并且对于工程技术人员来说,这种方法不易掌握;第二种方法就是根据地震作用下建筑结构的加速度反映,求出该结构体系的惯性力,将此惯性力作为一种反映地震影响的等效力,即地震作用,然后进行抗震计算,抗震规范实际上采用了第二种方法,即地震作用反应谱法。
实践也证明此方法更适合工程技术人员采用。
由于目前抗震规范中的地震作用反应谱仅考虑结构发生弹性变形情况下所得的反应谱,因此当结构某些部位发生非线性变形时,抗震规范中的反应谱就不能适用,而应采用弹塑性反应谱来进行计算。

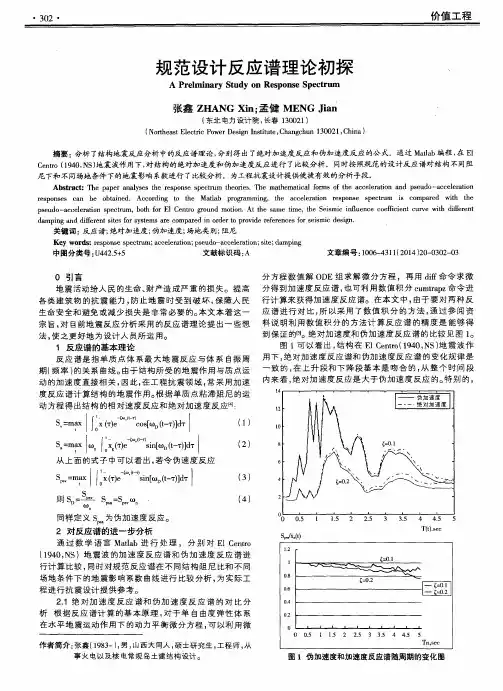
几类反应谱的概念差异及其意义连及设并几类反应谱的概念差异及其意义一,前言李杰(化工部抗震防灾研究室)反应谱理论是工程结构抗震设计的基础理论之一.近年来,关于反应谱的研究工作日趋复杂而广泛.例如,在《建筑抗震设计规范(GBJ11—89)》中给出的设计反应谱考虑了远,近震的影响,并将场地类别划分为四类而在"构筑物抗设计规范"(送审稿)中,则将场地参数连续化,通过场地指数给出具体设计反应谱在关于地震危险隆分析的研究中,提出了考虑震级,距离影响的基岩反应谱和基于地震危险性分析的一致危险性反应谱.在城市抗震设防区划的研究工作中,提出了双参数标定谱和考虑场地随机性影响的均值反应潜等.上述反应谱还都是基于确定性结构的弹性反应谱而言的,如果再进一步考虑结构参数的非确定性和结构进入非线性的可能性,还能衍生出更多种类的反应谱在这种复杂背景的另一方面,近年来在设计规范中对地震动参数的取值规定存在着相对放宽约束,趋向采取双轨制或多种考虑的倾向.例如,我国《建筑抗震设计规范(GBJll--89)》中就明确指出;"对做过抗震防灾规划的城市,可按批准的抗震设防区划(设防烈度或设计地震动参数)进行抗震设防".—般说来,经过批准的抗震设防区划,对区划范围内的场地都同时作出关于设防烈度和设计反应谱的具体规定.作者发现,在近年来一些藏市防灾规划7?1嘶中,规定的反应谱往往并未严格掌握不同类型的谱的含义,存在着误用,混用的现象,这种状况,有可能给工程设计带来混乱.有鉴于此,本文拟以确定性结构的弹性反应谱为背景,讨论几种常见类型谱的概念及工程意义,讨论的重点将放在关于反应谱概率意义的考虑方面.希望通过这种讨论,有助于澄清一些基本概念,为工程结构的抗震设计提供一些概念上的帮助二,地震反应谱与设计反应谱众所周知,反应谱是指单质点体系地震最大反应与结构自振周期之间的关系在这种一般意义的基础上,反应谱又有地震反应谱与设计反应谱的概念区别.所滑地震反应谱,是指针对具体地震记录计算的反应谱,例如,绝对加速度反应谱:,lnsa(∞)一lIaO)e一…'lJ0sin[o~(t—t)+2旺]d'rl(1)式中:一∞tga一√r=地震反应潜在本质上反映的是地震动强度与频谱特性,这是因为:任何一条地震反应谱曲线都是许许多多具有不同动力特性的单质点结构对一个地震动时程的动力最大反应按T排列起来的结果,因此,从总体上说,地震反应谱不反映具体的结构特陛,而是反映地震动的特性.换句话说,9地震反应谱是从动力特性沿频率方向"滑动"的单质点体系动力最大反应这个特殊角度来描述地震动特性的通过对不同地震记录的地震反威普的综合分析,将给出设计反应谱,在本质上, 设计反应谱是对设计地震力的一种规定. 这是困为,设计反应谱并不反映一次具体的地震动过程的特性,而是从工程设计的角度在总体上把握地震动特性.这种把握, 可以是统计平均意义上的把握,也可以是严格概率意义上的把握将设计反应谱与地震反应谱在概念上区分开来,有利于在更广泛的背景下研究设计地震力.图1是两类谱的—个典型对比.周期(9)圈1.地麓反瘟谱与设计反应谱三,几类反应谱的概念差异工程上,常将反应谱用地震影响系数曲线加以表示,即将反应谱除以重力加速度:1Oa—sa(2)g对上式加以变换Ⅱ:S—a.:K.8(3)g‰其中:K=‰称为地震系数8一sa/‰称为动力放大系数.这祥,就将反应谱分解为强度特性K和频谱特性日两个部分.由于实际的地震动受多种复杂因素影响,因此,地震动无论在强度还是在频谱含量上都具有强烈的随机性.在确定性结构弹性反应谱的框架范围内,不同类型的反应谱之间的差异主要表现在对这两个l逮机性的处理上面. 1?,规范设计反应谱这里以"建筑物抗震设计规范"(GBJ11--89)为背景讨论规范设计反应谱的基本思想是以地震区划给定的基本烈度作为设防烈度依据确定K,以历史地震记录的动力放大系数曲线的统计平均值为依据确定B.由于地震危险性分析技术的发展与应用,目前对K值的规定是具有严格概率含义的.例如,对于设防烈度,地震动加速度幅值的超越概率一般取为10.在此基础上,进—步考虑"小震不坏,中震可修,大震不倒"的设计思想,演绎出了两阶段设{十的方法.关于小震强度验算,地震动加速度幅值的超越概率为63.2,而关于大震变形验算,地震动加速度幅值的超越概率为2 ~3.然而,规范设计反应谱关于B的取值并无严格的概率含义,而只具有一种准概率含义的修正统计平均性.在规范的背景研究中,通常是将实际地震记录按场地条件,震级与距离条件分类,对于每_:类别内的地震记录样本,计算动力放大系数曲线, 进而选取一些离散周期点分别关于( (T),i=1,2,……}进行统计平均,以平均直的连线为基础进一步平滑,修整,使之成为标准的动力放大系数曲线.平滑,修整前后的0谱对比如图2.(b)修整后图2.反应港的修整规范设计反应谱合理地解决了关于地震动强度不确定性问题,面对频谱含量不确定性则只作了均随意义上的近似处理.并且,由于规范谱本质上是以加速度峰值标定反应谱(一般说来,这种标定仅适用于高频段),因此,设计反应谱所规定的地震力在不同谱值处的概率含义是不同的.换句话说,对于不同周期结构,按规范反应谱求得的设计地震力的概率保证率是不一致的.2,-一致危险睦反应谱一致危险陆反应谱的基本含义是在不同周朔处的反应谱值具有相同的超越概率值.这一类反应谱源于地震危险性分析的研究工作,根据对基岩地震记录反应谱的统计分析,可以建立不同周期点的基岩地震动衰减关系.通常,取震级与距离作为统计公式中的基本变量,在给定了震级与距离的前提下,可以由基岩反应谱的衰减关系中给出具体反应谱(图3),这样,便有了所谓考虑震级,距离影响的基岩反应谱的概念.从概率意义上看,这类反应谱只具有关于历史地震记录的统计均值含义,而不具有超越概率的含义.因此,可称此类谱为基岩均值反应谱.在地震小区划中,若采用危险震源法,即依据设防概率水平和地震动峰值的危险性曲线判断一组起控制作用的等效潜在震源,则可以基岩均值反应谱作为基岩地震动输入的依据.图基岩均值厦直谱在另一方面,若采用地震危险性分析方法关于主要周期点处分别计算参数Sa (T)的地震危险性曲线,则可以从这一簇地震危险性曲线中,按照统一设定的设防概率水准给出一致危险性反应谱(图4). 此时,反应谱曲线上的各点具有统一的超越概率.显然,这种做法所耗费的计算量是巨大的.1l图4-基岩●致危险性反应谱应该指出,基岩反应谱只反应了基岩地震动的特性.其中,基岩均值反应谱从统计平均意义上同时反映了K,13的随机性, —致危险性反应谱则主要是从幅值超越概率意义上反映了K,8的随机性影响.由于以统计平均的地震动衰减关系作媒介求取地震危险性曲线,一致危险性反应谱仍未完全考虑频谱特性的概率变化特征.12图5.随机场地反应谱3,考虑场地随机性影响的反应谱基岩反应谱只反映了基岩地震动的特性,因此不能直接作为设计谱.设计谱的获取尚应考虑场地条件的影响.由于场地土层分布特征的不确定性,场地土层刚度的变异性,使场地地震反应谱表现出显着的随机性,图5是用蒙特卡洛模拟方法计算的反应谱,土层参数的变异性使得反应谱的中民周期部分表现出巨大的离散性,这种离散性甚至高于不同地震动输入引起的反应谱变异(图8).这种对比,使我们可能直接从土层参数变异性的角度把握反应谱频率含量的变异性,而将地震动输入的变异性包括在其中而不单独考虑.固6.不同地菇输入的场地反应谱当采用均值反应谱概念时,可以以基岩均值反应谱为基础,利用随机场地地震反应分析方法确定场地均值反应谱f3(T). 而若采用基岩一致危险性反应谱作为输入,则可以采用随机场地反应分析方祛确定场地的等概率反应谱.从现有计算结果推断,由于土层剐度的影响,不同周期处0 (T)的分布将具有偏态分布(如对数正态分布)的特征.在考虑土层参数随机性影响时,场地地震动幅值亦有一定幅度的改变,这在规范反应谱中是难以反映的.4,双参数标定反应谮双参数标定反应谱将反应谱的蜘昔持征变化与橱值变化统一在一起考虑.其反应谱表达方式为(hn速度):r2laI+b】}T0≤T≤T】一1b2aLT】≤T≤T2()Lb3vjTT2≤T≤T式中,b,b,ba,r为标定常数,aj,Ⅵ为地震动0§值加遗度与峰值建度.T,T为反应谱拐点周期.Ts一3秒.根据拐点处连续条件可在T,T:与aJ,Ⅵ之间建立起定量关系.双参数反应谱,既适用于基岩反应谱,也适用于地表设计反应谱,所不同的仅在于,Ⅵ的取值和标定常数时的(T)的样本取值,即对于基岩反应谱,应取地震危险性分析给定的一致危险陛地震动参数a,v{ 和基岩记录(T)样本{对于设计反应谱,则应取基于场地地震危陛分析结果的地震动小区划分av值和相应B(T)掸率.作为一般设计谱,也可以取历史强震记录样本岛(T)来确定标定参数.双参数标定谱图例见图7.图7.双参数标定匣应谱从概率意义上看,双参数标定谱主要反映设计地震动强度的超越概率特征,而对频率含量钓不确定性同样是从等效统计均值的角度把握的因此,双参数标定反应谱是与规范设计反应谱平行的一种反应谱.它不能从概率意义上反映场地参数随机陛造成的影响.四,不同反应谱概念差异的工程意义不同类型的反应谱的概念差异有两方面的工程意义.其一,是工程设计中谱的选用l其二,是结构的抗震可靠度评定中对不同类型谱的要求.在工程设计中,规范反应谱,基于地震小区划的双参数标定谱,考虑场地参数变异性的均值反应谱,都可以直接应用于一般工程结构的设计之中,而基岩均值反应谱,基岩一致危险睦反应谱不能直接应用于一-般工程结构的设计之中.当工程结丰句的基础不是童接建于基岩之上时,尤其如此.在一些城市抗震设防区划中,以基岩一致危险性反应谱作为场地设计反应谱,是存在概念错误的.结构的抗震可靠度评定问题是建立在如下的一般准则之上的.结构在使用期限内的失效概率(R<s)=IPf(R<s】y)(y)dyJ口(5)式中,S为结构地震作用效应}R为结构抗力,(y)为给定时限的地震动幅值参数的概率密度函数取等效变量R—R/YS—s/v(6)则式(5)可变为:(R<s)一I(R<s】Y)'(Y)dYJ口(7)等效变量S是与结构动力放大系数等价的一类变量,可以证明,两者具有相同的变异系数和框类似的概率分布密度.于是,地震动幅值的不确定性(Y)可以通l3过地震危险性分析计算给出,而结构在给定地震动滴值条件下的抗震可靠度将与地震动频率含量的变异性取得联系a因此,在结构的抗震可靠度评定问题中,不可避免地要求事先确立13(T)谱的概率分布或变异系数(在假定日(T)为正态分布或对数正态分布前提下)由前节分析对比中我们知道:规范设计反应谱,双参数标定谱对应的B(T)谱均不具备日(T)在诸周期点的概率分布或变异系数的信息;基岩均值反应谱与一致危险性反应谱也不具备这种信息.仅有考虑场地土层随机参数变异性的反应谱可以提供这类信息,因此,从结构抗震可靠度评价角度看,采用考虑场地土层参数随机性的反应谱是较为合适的.关于规范设计反应谱和双参数标定谱,近年来也进行了关于日(T)谱变异性的研究,但这类研究—般需要大量实测强震加速度记录,且由于将不同场地或不同震级与距离条件的谱统一加以平均,因此离散性较大.而采用考虑场地参数变异性的方法研究B谱的变异性,可以弥补上述不足.从已有研究结果分析,作者倾向于认为,B谱的变异性,主要由于场地类别和场地土的变异性引起,而震级与距离;l起的日谱变异性可以包含在前述变异性之中, 当采用基岩均值潜或基岩一致危险性谱作为基岩输入计算地表地震反应时,问题尤为如此.五,结语反应谱主要反映了地震动的幅值特性与频谱特性,这两类特性都具有强烈的随机性.从一般意义上说,关于幅值特性的随机性可以从地震动幅值超越概率的角度加以把握,而关于频谱特性的随机性则应从动力放大系数曲线的变异性角度来考察. 在确定性结构弹性反应谱的概念范围内, 目前存在几类概念上有明显差异的反应谱,这些差异主要体现在对上述两类随机性的处理已无论在工程设计还是在结构抗震可靠度评价中,区分不同类型谱并适当地加以运用都具有重要的基础意义. (上接第74页)算法,该算法可以看作纽马克13法的推广; 3,该算法的优点在于不仅能考虑坝一基,坝一库和库.基界面上的相互作用,而且能够考虑波在地基和库水边界的吸收效应;4,利用该算法所做的几个反应分析表明,与由其他研究者得到的已有的结果符合得很好,说明了所提方法的有效性;5,通过几个反应分析,看来可以对坝一基一库系统的振动特性作出例如下列几点结论:(a)由地面运动冲击荷载产生的动水压力对第一阶振动反应的影响很小; (b)然而,动水压力趋于抑制高阶振型的振动并降低高阶振动频率;(c)地基与库水间的相互作用对动水压力的衰减有重大的影响译自:EarthquakeEngineeringand StructuralDynamics,v.22,n.3,1992.原题:AFE--BEMethodForD}mam—ieAnatysisofDam--Foundation——Rcserv—lotSystemintheTimeDomain.(卞启译)。

1.2 弹性反应谱在Maurice A. Biot []首先提出弹性反应谱的概念之后,经若干学者的发展,反应谱的概念已得到了较大程度的推广,且反应谱现在已被广泛地应用于地震工程的各个方面(如地震危险性分析、结构抗震设计、地震加速度记录的选择和调整及基于性能的地震工程等)。
目前,反应谱主要包括:傅立叶谱、弹性反应谱、弹塑性反应谱、能量反应谱和损伤谱等。
以下主要介绍弹性反应谱的定义,其余反应谱的定义与弹性反应谱类似。
所谓弹性反应谱就是在给定的地震加速度输入下,单自由度弹性系统的最大反应和体系的自振特征(自振周期或频率和阻尼比)之间的函数关系。
单自由度弹性系统的最大反应可以是:相对于地面的最大位移、相对于地面的最大速度、最大绝对加速度、拟速度和拟加速度。
在地面加速度的激励下,单自由度弹性系统的动力平衡方程为:)()()()(t u m t ku t u c t u m g -=++(1.1)式(1)的解可由Duhamel 积分求得:ττωτωτξωd t e u t u D t tg D)(sin )(1)()(0--=--⎰(1.2)将式(1.2)求导可得相对速度反应为:ττωτωτξωd t e ut uD t tg D)(sin )(1)()(0--=--⎰(1.3)将式(1.3)求导再与地面加速度相加可得绝对加速度反应为:ττωτωτξωd t e u t u t u D t tg Dg )(sin )(1)()()(0--=+--⎰(1.4)在式(1.1)~(1.4)中,m 为单自由度弹性体系的质量;c 为阻尼系数;k为体系的刚度系数;u(t)为体系相对于地面的位移;)(t u为体系的相对速度;)(t u 为体系的相对加速度;)(t u g 为地面加速度;ω为体系的无阻尼自振圆频率(ω2=2π/T=k/m );T 为体系自振周期;ζ为阻尼比(ζ=c/2m ω);ωD 为体系的有阻尼自振圆频率(21ξωω-=D )。


实振型分解反应谱法
1.振型分解原理
实振型分解反应谱法是一种基于结构振动特性的地震反应分析方法。
该方法将结构振动响应分解为若干个振型(模态)的叠加,从而在各个振型上单独求解地震反应。
2.反应谱理论
反应谱理论是研究结构在地震作用下的动力反应的重要工具。
它通过分析地震动输入的加速度、速度和位移反应谱,来描述结构在不同地震动频率下的响应。
3.地震动输入
地震动输入是地震反应分析的基础,包括地震动的峰值加速度、峰值速度和峰值位移等参数。
这些参数决定了结构在地震作用下的动力响应。
4.结构动力特性
结构动力特性包括结构的自振频率、阻尼比和振型等参数。
这些参数反映了结构在地震作用下的动力响应特性,是进行实振型分解反应谱法分析的基础。
5.阻尼模型
阻尼模型用于描述结构在振动过程中的能量耗散机制。
在实振型分解反应谱法中,通常采用阻尼比来描述结构在不同频率下的阻尼效应。
6.数值计算方法
实振型分解反应谱法的数值计算方法包括有限元法、有限差分法等。
这些方法通过离散化结构振动方程,求解结构在地震作用下的动力响应。
7.计算结果分析
通过对实振型分解反应谱法的计算结果进行分析,可以了解结构在不同地震动频率下的响应特征,从而评估结构的抗震性能。
8.工程应用
实振型分解反应谱法在工程结构抗震设计中得到广泛应用,可以用于评估结构的抗震性能、优化结构设计等方面。
同时,该方法也可以用于研究结构在地震作用下的动力响应和损伤机理。

反应谱法叠加原理
反应谱法是一种用于研究化学反应动力学和机理的光谱方法。
在这种方法中,通过监测反应过程中物质浓度的变化,结合光谱数据,可以获得反应速率常数、反应级数以及反应机理等信息。
叠加原理是物理学中一个基本原理,它适用于线性系统。
叠加原理表示:一个线性系统的响应可以视为多个独立输入信号的响应之和。
这意味着,如果我们知道系统的输入和单个输入信号的响应,那么我们可以通过叠加这些响应来计算系统的总响应。
在反应谱法中,叠加原理可以应用于多个反应步骤或多个反应物的同时存在。
根据叠加原理,我们可以将多个反应物的浓度变化分别表示为每个反应物的浓度变化之和。
这样,我们可以通过测量不同反应物的光谱信号,结合反应动力学模型,推断出各个反应步骤的速率常数和机理。
具体操作步骤如下:
1.监测反应过程中各反应物的浓度变化,得到浓度-时间曲线。
2.结合光谱数据,提取各个反应物的特征光谱信号。
3.根据叠加原理,将各个反应物的浓度变化表示为单独反应物的浓度变化之和。
4.建立反应动力学模型,包括反应速率方程和机理。
5.利用实验数据和模型计算各个反应步骤的速率常数和机理。
通过这种方法,反应谱法和叠加原理可以帮助我们更好地理解复杂化学反应的动力学和机理,为反应过程的控制和优化提供理论依据。

结构地震反应的分析方法与理论随着人们对地震和结构动力特性认识程度的加深,结构的抗震理论大体可以划分为静力分析、反应谱分析和动力分析三个阶段。
2.2.1静力分析理论水平静力抗震理论[25]始创于意大利,发展于日本。
该理论认为:结构所受的地震作作用可以简化为作用于结构的等效水平静力,其大小等于结构重力荷载乘以地震系数,即: /F G g kG =α= (2.1)静力理论认为结构是刚性的,故结构上任何一点的振动加速度均等于地震动加速度,结构上各部位单位质量所受到的地震作用是相等的。
它忽略了结构的变形特征,没有考虑结构的动力特性,与实际情况相差较远。
随着工程抗震研究的发展,对地震认识的深入,此法已经淘汰。
2.2.2反应谱理论上世纪40年代以后,由于计算机技术的应用,在取得了较多的强震记录的基础上,产生了反应谱理论。
反应谱分析方法[25][26]是一种将模态分析的结果与一个已知的谱联系起来计算模型的作用效应的分析技术。
反应谱是指单自由度体系最大地震反应与结构体系自振周期的关系曲线。
为了便于计算,《抗震规范》采用相对于重力加速度的单质点绝对最大加速度,即/a S g 与体系自振周期T 之间的关系作为设计用反应谱,并将/a S g 用α表示,称为地震影响系数,如图2-5所示。
单自由度弹体系水平地震反应微分方程为:()()()()0mx t cx t kx t mx t ++=- (2.2)由上式得:()()()()0m x t x t k x t c x t-+=+⎡⎤⎣⎦ (2.3) 上式等号右边的阻尼力项()cx t 相对于弹性恢复力项()kx t 来说是一个可以略去的微量,故:()()()0m x t x t kx t -+=⎡⎤⎣⎦ (2.4)由反应谱理论,水平地震作用为:/a a F mS S gG G ===α (2.5)/a S g α= (2.6)α——地震影响系数;a S ——质点的绝对最大加速度;图2-5 地震影响系数α曲线Fig.2-5 seismic influence coefficient α vurves上升阶段 ()max 0.45 5.5T α=+α (00.1T ≤≤) (2.7) 水平阶段 α=max α (0.1g T T <≤) (2.8)曲线下降段 max g T T γ2⎛⎫α=ηα ⎪⎝⎭(5g g T T T <≤) (2.9) 直线下降段 ()max 0.25g T T γ21⎡⎤α=η-η-α⎣⎦ (5 6.0g T T <≤) max α——地震影响系数最大值;g T ——场地特征周期。

一、地震反应谱的概念在给定的地震输入下,不同固有周期的地层或结构物将有不同的振动位移反应,这种反应的时程曲线是由多种频率成分组成的振动曲线叫地震反应谱,取对应于不同固有周期的位移时程曲线的最大值作为纵坐标,取所对应的固有的周期为横坐标,由此绘成曲线,供抗震设计中选用在设计周期下的相应振动幅值。
二、地震反应谱在结构地震反应分析理论发展中的作用1940年,美国比奥特(M.A.Biot)教授通过对强地震动记录的研究,首先提出反应谱这一概念,为抗震设计理论进人一个新的发展阶段奠定了基础,20世纪504代初,美网豪斯纳(G.W.Housener)等人发展了这一理论,并在美国加州抗震设计规范中首先采用反复谱概念作为抗震设计理论,以取代静力法。
这一理论至今仍然是我国和世界上许多国家工程结构设计规范中地震作用计算的理论基础。
反应谱理论考虑了结构的动力特性与地震动特性之间的动力关系,并保持了原有的静力理论的简单形式。
按照反应谱理论,单自由度弹性体系的结构物所受的最大地震基底剪力或地震作用为F=FEk=k⋅ββ⋅G式中G——结构的重力荷载代表值k——地震系数β——动力系数,与结构自振周期和阻尼比有关因而上式表明:结构地震作用的大小不仅与地震强度有关,还与结构的动力特性有关。
这也是地震作用区别于一般作用(荷载)的主要特征。
随着震害经验的积累和研究的不断深人,人们逐步认识到建筑场地(包括表层土的动力特性和覆盖层厚度)、震级和震中距对反应谱的影响。
考虑到这些因素,一般抗震规范中都规定了不同的反应谱形状。
利用振型分解原理,可有效地将上述概念用于多质点体系的抗震计算,这就是抗震设计规范中给出的振型分解反应谱法。
它以结构自由振动的N个振型为厂义坐标,将多质点体系的振动分解成n个独立的等效单质点体系的振动,然后利用反应谱概念求出各个(或前几个)振型的地震作用,并按一定的法则进行组合,即可求出结构总的地震作用。
三、从地震动响应推导出地震反应谱曲线对于单自由度弹性体系,通常把惯性力看作一种反映地震对结构体系影响的等效作用,即把动态作用转化为静态作用,并用其最大值来对结构进行抗震验算。
时程分析时地震波的选取及地震波的反应谱化摘要:目前我国规范要求结构计算中地震作用的计算方法一般为振型分解反应谱法。
时程分析法作为补充计算方法,在不规则、重要或较高建筑中采用。
进行时程分析时,首先面临正确选择输入的地震加速度时程曲线的问题。
时程曲线的选择是否满足规范的要求,则需要首先将时程曲线进行单自由度反应计算,得到其反应谱曲线,并按规范要求和规范反应谱进行对比和取舍。
本文通过介绍常用的数值计算方法及计算步骤,实现将地震加速度时程曲线计算转化成反应谱曲线,从而为特定工程在时程分析时地震波的选取提供帮助。
关键词:时程分析,地震波,反应谱,动力计算1 地震反应分析方法的发展过程结构的地震反应取决于地震动和结构特性。
因此,地震反应分析的水平也是随着人们对这两个方面认识的深入而提高的。
结构地震反应分析的发展可以分为静力法、反应谱法、动力分析法这三个阶段。
在动力分析法阶段中又可分为弹性和非弹性(或非线性)两个阶段。
[1]目前,在我国和其他许多国家的抗震设计规范中,广泛采用反应谱法确定地震作用,其中以加速度反应谱应用得最多。
反应谱是指:单自由度弹性体系在给定的地震作用下,某个最大反应量(如加速度、速度、位移等)与体系自振周期的关系曲线。
反应谱理论是指:结构物可以简化为多自由度体系,多自由度体系的地震反应可以按振型分解为多个单自由度体系反应的组合,每个单自由度体系的最大反应可以从反应谱求得。
其优点是物理概念清晰,计算方法较为简单,参数易于确定。
反应谱理论包括如下三个基本假定:1、结构物的地震反应是弹性的,可以采用叠加原理来进行振型组合;2、现有反应谱假定结构的所有支座处地震动完全相同;3、结构物最不利的地震反应为其最大地震反应,而与其他动力反应参数,如最大值附近的次数、概率、持时等无关。
[1]时程分析法是对结构物的运动微分方程直接进行逐步积分求解的一种动力分析方法。
由于此法是对运动方程直接求解,又称直接动力分析法。
抗震设计中反应谱得应用一.什么就是反应谱理论在房屋工程抗震研究中,反应谱就是重要得计算由结构动力特性所产生共振效应得方法、它得书面定义就是“在给定得地震加速度作用期间内,单质点体系得最大位移反应、速度反应与加速度反应随质点自振周期变化得曲线。
用作计算在地震作用下结构得内力与变形",反应谱理论考虑了结构动力特性与地震动特性之间得动力关系,通过反应谱来计算由结构动力特性(自振周期、振型与阻尼)所产生得共振效应,但其计算公式仍保留了早期静力理论得形式。
地震时结构所受得最大水平基底剪力,即总水平地震作用为:FEK = kβ(T)G式中,k为地震系数,β(T)则就是加速度反应谱Sa(T)与地震动最大加速度a得比值,它表示地震时结构振动加速度得放大倍数。
β(T)=Sa(T)/a反应谱理论建立在以下基本假定得基础上:1)结构得地震反应就是线弹性得,可以采用叠加原理进行振型组合;2)结构物所有支承处得地震动完全相同:3)结构物最不利地震反应为其最大地震反应:4)地震动得过程就是平稳随机过程。
二.实际房屋抗震设计中得应用为了进行建筑结构得抗震设计,必须首先求得地震作用下建筑结构各构件得内力。
一般而言,求解建筑结构在地震作用下构件内力得方法主要有两种,一种就是建立比较精确得动力学模型进行动力时程分析计算,这种方法比较费时费力,其精确度取决于动力学模型得准确性与所选取地震波就是否适当,并且对于工程技术人员来说,这种方法不易掌握;第二种方法就是根据地震作用下建筑结构得加速度反映,求出该结构体系得惯性力,将此惯性力作为一种反映地震影响得等效力,即地震作用,然后进行抗震计算,抗震规范实际上采用了第二种方法,即地震作用反应谱法。
实践也证明此方法更适合工程技术人员采用、由于目前抗震规范中得地震作用反应谱仅考虑结构发生弹性变形情况下所得得反应谱,因此当结构某些部位发生非线性变形时,抗震规范中得反应谱就不能适用,而应采用弹塑性反应谱来进行计算。
振型分解反应谱法公式推导过程一、振型分解反应谱法基本原理。
1. 多自由度体系的运动方程。
- 对于一个具有n个自由度的线性弹性结构体系,在地震作用下的运动方程为:M ẍ(t)+C ẋ(t)+Kx(t)= - M1ẍ_g(t)其中,M为质量矩阵(n× n阶),C为阻尼矩阵(n× n阶),K为刚度矩阵(n× n阶),ẍ(t)、ẋ(t)和x(t)分别为相对于地面的加速度、速度和位移向量(n维),ẍ_g(t)为地震地面加速度时程,1是元素全为1的列向量。
2. 振型分解。
- 假设多自由度体系的位移x(t)可以按照体系的振型φ_j(j = 1,2,·s,n)进行分解,即:x(t)=∑_j = 1^nφ_jq_j(t)其中,φ_j为第j阶振型向量(n维),q_j(t)为第j阶广义坐标(标量)。
- 将x(t)=∑_j = 1^nφ_jq_j(t)代入运动方程M ẍ(t)+C ẋ(t)+Kx(t)= - M1ẍ_g(t),然后左乘φ_i^T(φ_i的转置向量),得到:φ_i^TM∑_j = 1^nφ̈_jq_j(t)+φ_i^TC∑_j = 1^nφ̇_jq_j(t)+φ_i^TK∑_j = 1^nφ_jq_j(t)=-φ_i^TM1ẍ_g(t)- 由于振型具有正交性,即φ_i^TMφ_j=0(i≠ j),φ_i^TKφ_j=0(i≠ j),并且对于比例阻尼C = α M+β K,也有φ_i^TCφ_j=0(i≠ j)。
- 当i = j时,定义广义质量M_j^*=φ_j^TMφ_j,广义刚度K_j^*=φ_j^TKφ_j,广义阻尼C_j^*=φ_j^TCφ_j,则对于第j阶振型,有:M_j^*q_j(t)+C_j^*q_j(t)+K_j^*q_j(t)=-φ_j^TM1ẍ_g(t)进一步化为标准形式:q_j(t)+2ξ_jω_j q_j(t)+ω_j^2q_j(t)=-frac{φ_j^TM1}{M_j^*}ẍ_g(t)其中,ω_j=√((K_j)^*)/(M_{j)^*}为第j阶圆频率,ξ_j=frac{C_j^*}{2M_j^*ω_j}为第j阶阻尼比。