2018年高考文科数学分类汇编专题八立体几何

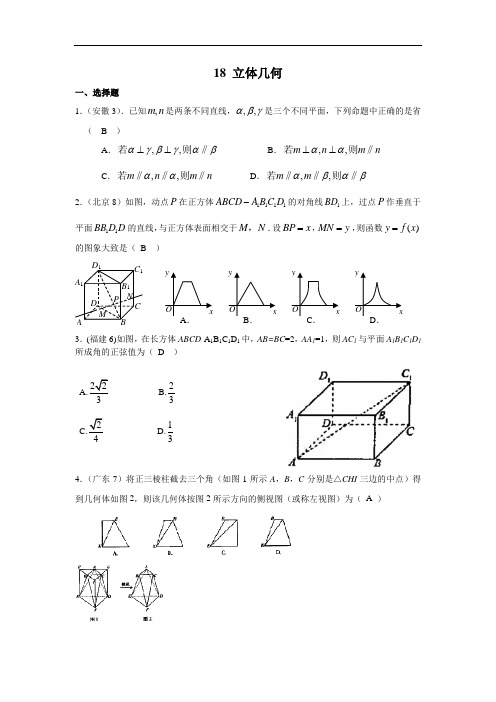
18 立体几何一、选择题1．（安徽3）．已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是省（ B ）A ．,,αγβγαβ⊥⊥若则‖B ．,,m n m n αα⊥⊥若则‖C ．,,m n m n αα若则‖‖‖D ．,,m m αβαβ若则‖‖‖2．（北京8）如图，动点P 在正方体1111ABCD A BC D -的对角线1BD 上，过点P 作垂直于平面11BB D D 的直线，与正方体表面相交于M N ，．设B P x =，MN y =，则函数()y f x =的图象大致是（ B ）3．(福建6)如图，在长方体ABCD -A 1B 1C 1D 1中，AB=BC =2，AA 1=1，则AC 1与平面A 1B 1C 1D 1所成角的正弦值为（ D ） A.223B.23C.24D.134．（广东7）将正三棱柱截去三个角（如图1所示A ，B ，C 分别是△CHI 三边的中点）得到几何体如图2，则该几何体按图2所示方向的侧视图（或称左视图）为（ A ）ABC DMNP A 1B 1C 1D 1 yxA ．OyxB ．OyxC ．Oyx D ．O5．（宁夏12）已知平面α⊥平面β，l αβ=，点A α∈，A l ∉，直线AB l ∥，直线AC l ⊥，直线m m αβ∥，∥，则下列四种位置关系中，不一定．．．成立的是（ D ） A ．AB m ∥B ．AC m ⊥C ．AB β∥D ．AC β⊥6．（湖南5）已知直线m,n 和平面βα,满足βα⊥⊥⊥,,a m n m ,则 ( D ).A n β⊥ ,//.βn B 或β⊂n α⊥n C . ,//.αn D 或α⊂n7．（湖南9）长方体1111ABCD A BC D -的8个顶点在同一个球面上，且AB=2，AD=3，11=AA ，则顶点A 、B 间的球面距离是( B )A ．42π B ．22πC ．π2D ．2π2 8．（江西9）．设直线m 与平面α相交但不．垂直，则下列说法中正确的是（ B ） A ．在平面α内有且只有一条直线与直线m 垂直 B ．过直线m 有且只有一个平面与平面α垂直 C ．与直线m 垂直的直线不．可能与平面α平行 D ．与直线m 平行的平面不．可能与平面α垂直 9．（辽宁12）在正方体1111ABCD A BC D -中，E F ，分别为棱1AA ，1CC 的中点，则在空间中与三条直线11A D ，EF ，CD 都相交的直线（ D ） A ．不存在B ．有且只有两条C ．有且只有三条D ．有无数条10．（全国Ⅰ11）已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 内的射影为ABC △的中心，则1AB 与底面ABC 所成角的正弦值等于（ B ）A ．13B ．23C ．33D ．2311．（全国Ⅱ8）正四棱锥的侧棱长为32，侧棱与底面所成的角为︒60，则该棱锥的体积为（ B ） A ．3 B ．6 C ．9 D ．18 12．（全国Ⅱ12）已知球的半径为2，相互垂直的两个平面分别截球面得两个圆．若两圆的公共弦长为2，则两圆的圆心距等于（ C ） A ．1B ．2C ．3D ．213．(山东6) 右图是一个几何体的三视图，根据图中数据，可得该几何体的表面积是（ D ）2A ．9πB ．10πC ．11πD ．12π 14．（上海13）给定空间中的直线l 及平面α．条件“直线l 与平面α内两条相交直线都垂直”是“直线l 与平面α垂直”的（ C ）Ａ．充分非必要条件 Ｂ．必要非充分条件C ．充要条件 Ｄ．既非充分又非必要条件15．（四川８）设M 是球心O 的半径OP 的中点，分别过,M O 作垂直于OP 的平面，截球面得两个圆，则这两个圆的面积比值为：( D ) （Ａ）41 （Ｂ）12 （Ｃ）23 （Ｄ）3416．（四川10）设直线l ⊂平面α，过平面α外一点A 与,l α都成030角的直线有且只有：( B )（Ａ）１条 （Ｂ）２条 （Ｃ）３条 （Ｄ）４条 17．（四川12）若三棱柱的一个侧面是边长为2的正方形，另外两个侧面都是有一个内角为060的菱形，则该棱柱的体积等于( B )（Ａ）2 （Ｂ）22 （Ｃ）32 （Ｄ）42 18．(天津5) 设a b ，是两条直线，αβ，是两个平面，则a b ⊥的一个充分条件是（ C ） A ．a b αβαβ⊥⊥，∥， B ．a b αβαβ⊥⊥，，∥ C ．a b αβαβ⊂⊥，，∥D ．a b αβαβ⊂⊥，∥，19．（浙江9）对两条不相交的空间直线a 和b ，必定存在平面α，使得 ( B ) （A ）,a b αα⊂⊂ （B ）,//a b αα⊂ （C ）,a b αα⊥⊥ （D ）,a b αα⊂⊥20．(重庆11)如题（11）图，模块①－⑤均由4个棱长为1的小正方体构成，模块⑥由15个棱长为1的小正方体构成.现从模块①－⑤中选出三个放到模块⑥上，使得模块⑥成为一个棱长为3的大正方体.则下列选择方案中，能够完成任务的为 ( A )(A)模块①，②，⑤ (B)模块①，③，⑤ (C)模块②，④，⑥ (D)模块③，④，⑤21．(湖北4).用与球必距离为1的平面去截面面积为π，则球的体积为 ( D ) A.323π B.83π C.82π D. 823π22．(陕西8)长方体1111ABCD A BC D -的各顶点都在半径为1的球面上,其中1::2:1:3A B A D A A=,则两,A B 点的球面距离为( C ) A ．4πB ．3π C ．2π D ．23π 23．(陕西10) 如图，l A B A B αβαβαβ⊥=∈∈，，，，，到l 的距离分别是a 和b ，AB 与αβ，所成的角分别是θ和ϕ，AB 在αβ，内的射影分别是m 和n ，若a b >，则（ D ） A ．m n θϕ>>， B ．m n θϕ><， C ．m n θϕ<<，D ．m n θϕ<>，二、填空题1．（安徽16）已知点,,,A B C D 在同一个球面上,,AB BCD ⊥平面,BC CD ⊥若6,AB =213,AC =8AD =,则,B C 两点间的球面距离是43π2．（福建15）若三棱锥的三条侧棱两两垂直，且侧棱长均为3，则其外接球的表面积是 . 9π3．（广东15）（几何证明选讲选做题）已知PA 是圆O 的切点，切点为A ，A B abl αβMA BDCOPA ＝2.AC 是圆O 的直径，PC 与圆O 交于B 点，PB ＝1，则圆O 的半径R =________.3 4．（宁夏14）一个六棱柱的底面是正六边形，其侧棱垂直底面．已知该六棱柱的顶点都在同一个球面上，且该六棱柱的高为3，底面周长为3，则这个球的体积为 ．43π 5．（江西15）连结球面上两点的线段称为球的弦．半径为4的球的两条弦AB CD 、的长度分别等于27、43，每条弦的两端都在球面上运动，则两弦中点之间距离的最大值为 ．56．（辽宁14）在体积为43π的球的表面上有A 、B ，C 三点，AB =1，BC =2，A ，C 两点的球面距离为33π，则球心到平面ABC 的距离为_________．327．（全国Ⅰ16）已知菱形ABCD 中，2AB =，120A ∠=，沿对角线BD 将ABD △折起，使二面角A BD C --为120，则点A 到BCD △所在平面的距离等于 ．328．（全国Ⅱ16）平面内的一个四边形为平行四边形的充要条件有多个，如两组对边分别平行，类似地，写出空间中的一个四棱柱为平行六面体的两个充要条件： 充要条件① ； 充要条件② ． （写出你认为正确的两个充要条件）两组相对侧面分别平行；一组相对侧面平行且全等；对角线交于一点；底面是平行四边形． 注：上面给出了四个充要条件．如果考生写出其他正确答案，同样给分．9．（浙江15）已知球O 的面上四点A 、B 、C 、D ，DA ⊥平面ABC ，AB ⊥BC ，DA=AB=BC=3，则球O 点体积等于 。

【母题原题1】【2018新课标1，文18】如图，在平行四边形中，，，以为折痕将△折起，使点到达点的位置，且．（1）证明：平面平面；（2）为线段上一点，为线段上一点，且，求三棱锥的体积．点睛：该题考查的是有关立体几何的问题，涉及到的知识点有面面垂直的判定以及三棱锥的体积的求解，在解题的过程中，需要清楚题中的有关垂直的直线的位置，结合线面垂直的判定定理证得线面垂直，之后应用面面垂直的判定定理证得面面垂直，需要明确线线垂直、线面垂直和面面垂直的关系，在求三棱锥的体积的时候，注意应用体积公式求解即可. 学￥科网【母题原题2】【2017新课标1，文18】如图,在四棱锥P-ABCD中,AB∥CD,且∠BAP=∠CDP=90°.(1)证明:平面P AB⊥平面P AD;(2)若P A=PD=AB=DC,∠APD=90°,且四棱锥P-ABCD的体积为,求该四棱锥的侧面积.【解析】(1)由已知∠BAP=∠CDP=90°,得AB⊥AP,CD⊥PD.由于AB∥CD,故AB⊥PD,从而AB⊥平面PAD.又AB?平面P AB,所以平面P AB⊥平面PAD.(2)【母题原题3】【2016新课标1，文18】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6.顶点P在平面ABC内的正投影为点D,D在平面P AB 内的正投影为点E,连结PE并延长交AB于点G.(Ⅰ)证明:G是AB的中点;(Ⅱ)在答题卡第(18)题图中作出点E在平面P AC内的正投影F(说明作法及理由),并求四面体PDEF的体积.【解析】(Ⅰ)因为P在平面ABC内的正投影为D,所以AB⊥PD.因为D在平面P AB内的正投影为E,所以AB⊥DE.所以AB⊥平面PED,故AB⊥PG.又由已知可得,P A=PB,从而G是AB的中点.(Ⅱ)在平面P AB内,过点E作PB的平行线交PA于点F,F即为E在平面P AC内的正投影.。

5.立体几何1 .【2018年浙江卷】已知四棱锥SABCD勺底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为0 1, SE与平面ABCD所成的角为0 2,二面角SABC的平面角为0 3,贝UA. 0 1< 0 2< 0 3B. 0 3< 0 2< 0 1C. 0 1<0 3< 0 2D. 0 2< 0 3< 0 1【答案】D【解析】分析:分别作出线线角、线面角以及二面角，再构造直角三角形，根据边的大小关系确定角的大小关系. 详解：设。

为正方形也仞的中心』耐为也中点，过迟作恥的平行线肿，交仞干形过。

作QM垂直跻于M连接旳朗 g则$0垂直于底面册CDQA/垂直干血，因此=fl1#zSF（7 = G3I Z SM0=%从而tan兔二空二空』tan禺二空」tan虬二弓因为SN >SO f E0 > 0M ?所以tan0t> tanS a>tan0j即■EW1EC^OAF =B丄工內筈血，选D.点睛：线线角找平行，线面角找垂直，面面角找垂面2.[ 2018年浙江卷】某几何体的三视图如图所示（单位：cm）,则该几何体的体积（单位：cm3）是俯视图A. 2B. 4C. 6D. 8[答案】C[解析】分析：先还原几何体为一直四棱柱，再根据柱体体积公式求结果详解：根据三视图可得几何体为一个直四棱柱，高为2,底面为直角梯形，上下底分别为 1 , 2,梯形的高为2,因此几何体的体积为器（1+2）X2X2=6选C.点睛：先由几何体的三视图还原几何体的形状，再在具体几何体中求体积或表面积等•3.[ 2018年文北京卷】某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为【答案】CH—j •樽I T ―- 2 -------- H【解析】分析：根据三视图还原几何体，利用勾股定理求出棱长，再利用勾股定理逆定理判断直角三角形的个数一详解：由三视團可得四棱锥卩—^CD｝在四棱锥卩-佔仞中，PD =21AD=21CD = 2t AB = l,由勾股定理可知:“ =2^2, PC = 迈FB =玉B€=VS,®］在四棱锥中’直角三甬形有zdPA^APC^APAS共三个，故选C.«ff点睛：此题考查三视图相关知识，解题时可将简单几何体放在正方体或长方体中进行还原，分析线面、线线垂直关系，利用勾股定理求出每条棱长，进而可进行棱长、表面积、体积等相关问题的求解4.【2018年新课标I卷文】在长方体厂工：中，「' ，—与平面处：匚：「所成的角为.,则该长方体的体积为A. '、B. .C. .D.【答案】C【解折】分析：首先画出长方体朋CD -金爲GL利用题中条件」得到^3=30；根^AB=2,求得= 2V3,可以确走=2V2,之后利用长方体的体积公式详解：在长方体朋仞—&民G6中，连接如根据线面甬的定义可知乙忙』二占叭因为胭=2,所以BG = 迅从而求得爼=2V2,所臥该长方体的体积为$二Z其2 X 2屈"妊故选U点睛：该题考查的是长方体的体积的求解问题，在解题的过程中，需要明确长方体的体积公式为长宽高的乘积，而题中的条件只有两个值，所以利用题中的条件求解另一条边的长久显得尤为重要，此时就需要明确线面角的定义，从而得到量之间的关系，从而求得结果5.【2018年新课标I卷文】已知圆柱的上、下底面的中心分别为1 ,，过直线'的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A 12jSnB 12nC 8^5TT D10n【答案】B【解析】分析：首先根据正方形的面积求得正方形的边长，从而进一步确定圆柱的底面圆半径与圆柱的高，从而利用相关公式求得圆柱的表面积•详解：根据题意，可得截面是边长为•的正方形，结合圆柱的特征，可知该圆柱的底面为半径是•的圆,且高为•，所以其表面积为％•二：+ .「上，一 V,故选B.点睛：该题考查的是有关圆柱的表面积的求解问题，在解题的过程中，需要利用题的条件确定圆柱的相关量，即圆柱的底面圆的半径以及圆柱的高，在求圆柱的表面积的时候，一定要注意是两个底面圆与侧面积的和• 6 .【2018年全国卷川文】设叙，閉;.『:■饭是同一个半径为4的球的球面上四点，阳聘为等边三角形且其面积为妝矣，则三棱锥紀朋£体积的最大值为A. B. C. D.【答案】B【解析】分析：作虱DjhjMO 2球的交点，点皿为三角形ABC的重心，判断出当DM丄平面AB时，三棱锥D-ABCft积最犬，然后进行计算可得中详解：如團所示，点M为三角形ABC的重心E为AC中点，当DM丄平面ABtM，三樓锥D-ABcf*积最犬，此时j 00 = OB = R = 4 »L砒-—?1B3= 9^5，A AH-"点就为三甬开乡ABC的重心』2:、BM = qEE =2V3； Rtfi ABC中，有=嗣阶一册丁=2^ -r™ = 0D + 0M = 4 + 2 = 6,毗ju旷尹潦汀」诙，故选B.点睛：本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当刚」平面审朦时，三棱锥皿閑廉体积最大很关键，由M为三角形ABC的重心，计算得到訓二;菖二祸再由勾股定理得到0M进而得到结果，属于较难题型。

2018高考数学热点题型--立体几何（文科有解析）立体几何热点一平行、垂直关系的证明与体积的计算以空间几何体(主要是柱、锥或简单组合体)为载体，通过空间平行、垂直关系的论证命制，主要考查公理4及线、面平行与垂直的判定定理与性质定理，常与平面图形的有关性质及体积的计算等知识交汇考查，考查学生的空间想象能力和推理论证能力以及转化与化归思想，一般以解答题的形式出现，难度中等.【例1】如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.(1)证明：平面AEC⊥平面BED；(2)若∠ABC＝120°，AE⊥EC，三棱锥E－ACD的体积为63，求该三棱锥的侧面积.(1)证明因为四边形ABCD为菱形，所以AC⊥BD.因为BE⊥平面ABCD，AC&#8834;平面ABCD，所以AC⊥BE.又BD∩BE＝B，故AC⊥平面BED.又AC&#8834;平面AEC，所以平面AEC⊥平面BED.(2)解设AB＝x，在菱形ABCD中，由∠ABC＝120°，可得AG＝GC＝32x，GB＝GD＝x2.因为AE⊥EC，所以在Rt△AEC中，可得EG＝32x.由BE⊥平面ABCD，BG&#8834;平面ABCD，得BE⊥BG，知△EBG为直角三角形，可得BE＝22x.由已知得，三棱锥E－ACD的体积V三棱锥E－ACD＝13×12ACGDBE＝624x3＝63，故x＝2.从而可得AE＝EC＝ED＝6.所以△EAC的面积为3，△EAD的面积与△ECD的面积均为5.故三棱锥E－ACD的侧面积为3＋25.【类题通法】第一步：由线面垂直的性质，得AC⊥BE.第二步：根据线面、面面垂直的判定定理，得平面AEC⊥平面BED.第三步：由体积公式计算底面菱形的边长.第四步：计算各个侧面三角形的面积，得出结论.第五步：查看关键点，检验反思，规范步骤.【对点训练】在三棱锥V－ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC＝BC＝2，O，M分别为AB，VA的中点.(1)求证：VB∥平面MOC；(2)求证：平面MOC⊥平面VAB；(3)求三棱锥V－ABC的体积.(1)证明因为O，M分别为AB，VA的中点，所以OM∥VB，又因为VB&#8836;平面MOC，OM&#8834;平面MOC，所以VB∥平面MOC.(2)证明因为AC＝BC，O为AB的中点，所以OC⊥AB.又因为平面VAB⊥平面ABC，平面VAB∩平面ABC＝AB，且OC&#8834;平面ABC，所以OC⊥平面VAB.又OC&#8834;平面MOC，所以平面MOC⊥平面VAB.(3)解在等腰直角三角形ACB中，AC＝BC＝2，所以AB＝2，OC＝1，所以等边三角形VAB的面积S△VAB ＝3.又因为OC⊥平面VAB，所以三棱锥C－VAB的体积等于13OCS△VAB＝33.又因为三棱锥V－ABC与三棱锥C－VAB的体积相等，所以三棱锥V－ABC的体积为33.热点二平面图形折叠成空间几何体先将平面图形折叠成空间几何体，再以其为载体研究其中的线、面间的位置关系与计算有关的几何量是近几年高考考查立体几何的一类重要考向，它很好地将平面图形拓展成空间图形，同时也为空间立体图形向平面图形转化提供了具体形象的途径，是高考深层次上考查空间想象能力的主要方向.【例2】如图，菱形ABCD的对角线AC与BD交于点O，点E，F分别在AD，CD上，AE＝CF，EF交BD于点H，将△DEF沿EF折到△D′EF的位置.(1)证明：AC⊥HD′；(2)若AB＝5，AC＝6，AE＝54，OD′＝22，求五棱锥D′－ABCFE的体积.(1)证明由已知得AC⊥BD，AD＝CD，又由AE＝CF得AEAD ＝CFCD，故AC∥E F，由此得EF⊥HD，故EF⊥HD′，所以AC⊥HD′.(2)解由EF∥AC得OHDO＝AEAD＝14.由AB＝5，AC＝6得DO＝BO＝AB2－AO2＝4，所以OH＝1，D′H＝DH＝3，于是OD′2＋OH2＝(22)2＋12＝9＝D′H2，故OD′⊥OH.由(1)知AC⊥HD′，又AC⊥BD，BD∩HD′＝H，所以AC⊥平面BHD′，于是AC⊥OD′，又由OD′⊥OH，AC∩OH＝O，所以OD′⊥平面ABC.又由EFAC＝DHDO得EF＝92.五边形ABCFE的面积S＝12×6×8－12×92×3＝694.所以五棱锥D′－ABCFE的体积V＝13×694×22＝2322.【类题通法】(1)①利用AC与EF平行，转化为证明EF与HD′垂直；②求五棱锥的体积需先求棱锥的高及底面的面积，结合图形特征可以发现OD′是棱锥的高，而底面的面积可以利用菱形ABCD与△DEF面积的差求解，这样就将问题转化为证明OD′与底面垂直以及求△DEF的面积问题了.(2)解决与折叠有关的问题的关键是搞清折叠前后的变化量和不变量，一般情况下，线段的长度是不变量，而位置关系往往会发生变化，抓住不变量是解决问题的突破口.【对点训练】如图1所示，在Rt△ABC中，∠C＝90°，D，E分别为AC，AB的中点，点F为线段CD上的一点，将△ADE沿DE折起到△A1DE的位置，使A1F⊥CD，如图2所示.(1)求证：A1F⊥BE；(2)线段A1B上是否存在点Q，使A1C⊥平面DEQ？说明理由.(1)证明由已知，得AC⊥BC，且DE∥BC.所以DE⊥AC，则DE⊥DC，DE⊥DA1，又因为DC∩DA1＝D，所以DE⊥平面A1DC.由于A1F&#8834;平面A1DC，所以DE⊥A1F.又因为A1F⊥CD，CD∩DE＝D，所以A1F⊥平面BCDE，又BE&#8834;平面BCDE，所以A1F⊥BE.(2)解线段A1B上存在点Q，使A1C⊥平面DEQ.理由如下：如图所示，分别取A1C，A1B的中点P，Q，则PQ∥BC.又因为DE∥BC，所以DE∥PQ.所以平面DEQ即为平面DEP.由(1)知，DE⊥平面A1DC，所以DE⊥A1C.又因为P是等腰△DA1C底边A1C的中点，所以A1C⊥DP，又DE∩DP＝D，所以A1C⊥平面DEP.从而A1C⊥平面DEQ.故线段A1B上存在点Q，使得A1C⊥平面DEQ.热点三线、面位置关系中的开放存在性问题是否存在某点或某参数，使得某种线、面位置关系成立问题，是近几年高考命题的热点，常以解答题中最后一问的形式出现，一般有三种类型：(1)条件追溯型；(2)存在探索型；(3)方法类比探索型.【例3】如图所示，在四棱锥P－ABCD中，底面ABCD是边长为a的正方形，侧面PAD⊥底面ABCD，且E，F分别为PC，BD的中点.(1)求证：EF∥平面PAD；(2)在线段CD上是否存在一点G，使得平面EFG⊥平面PDC？若存在，请说明其位置，并加以证明；若不存在，请说明理由.(1)证明如图所示，连接AC，在四棱锥P－ABCD中，底面ABCD是边长为a的正方形，且点F为对角线BD的中点.所以对角线AC经过点F，又在△PAC中，点E为PC的中点，所以EF为△PAC的中位线，所以EF∥PA，又PA&#8834;平面PAD，EF&#8836;平面PAD，所以EF∥平面解存在满足要求的点G.证明如下：在线段CD上存在一点G为CD的中点，使得平面EFG⊥平面PDC，因为底面ABCD是边长为a的正方形，所以CD⊥AD.又侧面PAD⊥底面ABCD，CD&#8834;平面ABCD，侧面PAD∩平面ABCD＝AD，所以CD⊥平面PAD.又EF∥平面PAD，所以CD⊥EF.取CD中点G，连接FG，EG.因为F为BD中点，所以FG∥AD.又CD⊥AD，所以FG⊥CD，又FG∩EF＝F，所以CD⊥平面EFG，又CD&#8834;平面PDC，所以平面EFG⊥平面PDC.【类题通法】(1)在立体几何的平行关系问题中，“中点”是经常使用的一个特殊点，通过找“中点”，连“中点”，即可出现平行线，而线线平行是平行关系的根本.(2)第(2)问是探索开放性问题，采用了先猜后证，即先观察与尝试给出条件再加以证明，对于命题结论的探索，常从条件出发，探索出要求的结论是什么，对于探索结论是否存在，求解时常假设结论存在，再寻找与条件相容或者矛盾的结论.【对点训练】如图，四棱锥S－ABCD的底面是正方形，每条侧棱的长都是底面边长的2倍，P为侧棱SD上的点.(1)求证：AC⊥SD；(2)若SD⊥平面PAC，则侧棱SC上是否存在一点E，使得BE∥平面PAC？若存在，求SE∶EC；若不存在，试说明理由.(1)证明连接BD，设AC交BD于点O，连接SO，由题意得四棱锥S－ABCD是正四棱锥，所以SO⊥AC.在正方形ABCD中，AC⊥BD，又SO∩BD＝O，所以AC⊥平面SBD，因为SD&#8834;平面SBD，所以AC⊥SD.(2)解在棱SC上存在一点E，使得BE∥平面PAC.连接OP.设正方形ABCD的边长为a，则SC＝SD＝2a.由SD⊥平面PAC得SD⊥PC，易求得PD＝2a4.故可在SP上取一点N，使得PN＝PD.过点N作PC的平行线与SC交于点E，连接BE，BN.在△BDN中，易得BN∥PO，又因为NE∥PC，NE&#8834;平面BNE，BN&#8834;平面BNE，BN∩N E＝N，PO&#8834;平面PAC，PC&#8834;平面PAC，PO∩PC＝P，所以平面BEN∥平面PAC，所以BE∥平面PAC.因为SN∶NP＝2∶1，所以SE∶EC＝2∶1.。

【立体几何型解答题高考数学试题汇编（2018年全国卷）】理科试题【2018年全国卷Ⅰ理科第18题】如图，四边形ABCD 为正方形,,E F 分别为,AD BC 的中 点,以DF 为折痕把DFC ∆折起，使点C 到达点P 的位置,且.BF DF ⊥ （1）证明：平面PEF ⊥平面ABFD ； （2）求DP 与平面ABFD 所成角的正弦值.【2018年全国卷Ⅱ理科第20题】如图,在三棱锥P ABC -中,AB BC ==PA PB ==4,PC AC ==O 为AC 的中点． （1）证明:PO ⊥平面ABC ； （2）若点M 在棱BC 上,且二面角M PA C --为30,求PC 与平面PAM 所成角的正弦值．【2018年全国卷Ⅲ理科第19题】如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于,C D 的点．（1）证明：平面AMD ⊥平面BMC ；（2）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成二面角的正弦值．C AAA文科试题【2018年全国卷Ⅰ文科第18题】如图,在平行四边形ABCM 中, 3,AB AC ==ACM ∠90,=以AC 为折痕将ACM ∆折起,使点M 到达点D 的位置,且AB DA ⊥． （1）证明：平面ACD ⊥平面;ABC（2）Q 为线段AD 上一点,P 为线段BC 上一点，且2,3BP DQ DA ==求三棱锥Q ABP-的体积．【2018年全国卷Ⅱ文科第20题】如图,在三棱锥P ABC -中,AB BC ==PA PB ==4,PC AC ==O 为AC 的中点． （1）证明:PO ⊥平面ABC ；（2）若点M 在棱BC 上,且2,MC MB =求点C 与平面POM 的距离．【2018年全国卷Ⅲ文科第19题】如图，矩形ABCD 所在平面与半圆弧CD 所在平面垂直，M 是CD 上异于,C D 的点．（1）证明：平面AMD ⊥平面BMC ； （2）在线段AM 上是否存在点,P 使得MC平面PBD ?说明理由．BAA。

8．2 空间几何体的表面积与体积1．柱体、锥体、台体的表面积(1)直棱柱、正棱锥、正棱台的侧面积S直棱柱侧＝____________，S正棱锥侧＝____________，S正棱台侧＝__________(其中C，C′为底面周长，h为高，h′为斜高)．(2)圆柱、圆锥、圆台的侧面积S圆柱侧＝________，S圆锥侧＝________，S圆台侧＝________(其中r，r′为底面半径，l为母线长)．(3)柱或台的表面积等于________与__________的和，锥体的表面积等于________与__________的和．2．柱体、锥体、台体的体积(1)棱柱、棱锥、棱台的体积V棱柱＝__________，V棱锥＝__________，V棱台＝__________(其中S，S′为底面积，h为高)．(2)圆柱、圆锥、圆台的体积V圆柱＝__________，V圆锥＝__________，V圆台＝__________(其中r，r′为底面圆的半径，h为高)．3．球的表面积与体积(1)半径为R的球的表面积S球＝________．(2)半径为R的球的体积V球＝___________.自查自纠1．(1)Ch 12Ch′12()C＋C′h′(2)2πrlπrlπ(r＋r′)l(3)侧面积两个底面积侧面积一个底面积2．(1)Sh 13Sh13h()S＋SS′＋S′(2)πr2h 13πr2h13πh()r2＋rr′＋r′23．(1)4πR2(2)43πR3已知圆锥的正视图是边长为2的等边三角形，则该圆锥体积为( )A.2π2B.2πC.3π3D.3π解：易知圆锥的底面直径为2，母线长为2，则该圆锥的高为22-12＝3，因此其体积是13π·12×3＝3π3.故选C.一个长方体共一顶点的三个面的面积分别是2，3，6，则这个长方体的体对角线的长是( )A．2 3 B．3 2 C．6 D. 6解：设长方体的长、宽、高分别为a，b，c，则有ab＝2，ac＝3，bc＝6，解得a＝1，b＝2，c＝3，则长方体的体对角线的长l＝a2＋b2＋c2＝6.故选D.(2016·全国卷Ⅰ)如图，某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径．若该几何体的体积是28π3，则它的表面积是( )A．17πB．18πC．20πD．28π(解：由三视图作出该四棱柱的直观图如图所示，为等腰梯形．由三视图给出的数据容易求出(1＋2)×1＝32，所以四棱柱的体积为故填32.类型一 空间几何体的面积问题2016·全国卷Ⅲ)如图，网格纸上小正方，粗实线画出的是某多面体的三视图，36 5 B ．54＋1890D ．81解：由三视图可得该几何体是平行六面体，上下3的正方形，故面积都是9，前后两个侧面是平行四边形，一边长为3，该边上的高为B ．π＋3D.52π＋解：由三视图可知，该几何体是半个圆锥，且母解：如图，设球的一条半径与圆柱相应的母线的，圆柱侧面积S ＝2π×4sin ＝π4时，S 取最大值球的表面积与该圆柱的侧面积之差为【点拨】根据球的性质，内接圆柱上、下底面中心连线的中点为球心，且圆柱的上、下底面圆周均在球面上，球心和圆柱的上、下底面圆上的点的连线与母线的夹角相等，这些为我们建立圆柱的侧面积与上述夹角之间的函数关系提供了依据．·陕西)一个几何体的三视图如图所示，则该几何体的表面积为( )B ．4πC ．2解：该几何体为半圆柱，底面半径为1，高为π×12＋2×2＋12×2π×1×2＝类型三 空间多面体的体积问题如图，在多面体ABCDEF 中，已知边长为1的正方形，且△ADE ，△BCF 均为正三角形，2，则该多面体的体积为( )B.33C.43如图，过A ，B 两点分别作AM ，BN 垂直于，N ，连接DM ，CN ，可证得DM 则多面体ABCDEF 分为三部分，即多面体的体积＋V E ­AMD ＋V F ­BNC .依题意知AEFB 为等腰梯形．△DME Rt △CNF ，所以EM ＝NF ＝，所以BN ＝32. ，则H 为BC 的中点，12 B．18 C．24解：由三视图可知该几何体是由一个直三棱柱去掉一个三棱锥得到的．所以该几何体的体积为×3×4×3＝24.故选C.类型四空间旋转体的体积问题已知某几何体的三视图如图所示，其中，视图、侧(左)视图均是由三角形与半圆构成，＋12B.4π3＋16＋16D.2π3＋12由三视图可得该几何体的上部是一个三棱锥，下部是半球，根据三视图中的数据可得V＝12⎭⎪⎫12×1×1×1＝2π6＋16.故选C.【点拨】根据已知三视图想象出该几何体的直观图，然后分析该几何体的组成，再用对应的体积公式(2015·重庆)某几何体的三视图如图所示，则该几何体的体积为( )π B.23＋2π D.23＋2π解：由三视图容易看出，该几何体是由一个半圆B．2πC．3π解：由三视图可知，该几何体为半径为r＝表面积为底面圆面积加上半球面的面积，位置有关 位置有关 Q 位置都有关 Q 位置均无关，是定值＝V Q ­A ′EF ＝13×⎝ ⎛12×的体积与点E ，F .ABC ­A 1B 1C 1的底面边长为的中点，则三棱锥A ．32C ．1 解：在正三棱柱ABC ­A 1B 1C 1中，易知面面垂直的性质定理可得AD ⊥平面·AD ＝13×12×2×．22斛 C ．36斛 D ．解：设圆锥底面半径为r ，因为米锥底部弧长为r ＝16≈16尺，所以米堆的体积为B.17C.16解：设正方体棱长为a ，则截去部分为三棱锥，其体积VA ­A 1B 1D 1＝13×12a 3＝16a 3，剩余部分的56a 3，所以截去部分体积与剩余部分体故选D .是球O 半径OP 上的两点，且解：由三视图作出该几何体的直观图如图所示，ABC 是等腰三角形．点D 为底边AC 的中点．3，BD ⊥AC ，BD ＝1，SD ⊥底面ABC ，SD ＝­ABC ＝13SD ·S △ABC ＝13×1×12×1×23＝33.故填．(2014·江苏)设甲、乙两个圆柱的底面积分别S 2，体积分别为V 1，V 2.若它们的侧面积相等，，则V 1V 2的值是____________． 解：设两圆柱底面半径为r 1，r 2，两圆柱高为＝94，r 1r 2＝32，又两圆柱侧面积相等，所以2πr 2πr解：由题意可设直角梯形上底、下底和高为，它们分别为圆台的上、下底半径和高．如OA 于C ，则Rt △ABC ＝2x ，BC ＝O ′O ＝2＋（5x ）2＝3x .9.·上海)底面边长为其表面展开图是三角形P 1P 2P 3.如图，的边长及三棱锥的体积V .解：由正三棱锥P ­ABC 的性质及其表面展开图是，C 分别是△P 1P 2P 3三边的中点，且依三角形中位线定理可得易判断正三棱锥P ­ABC 为棱长为V ＝212×23＝223. ·全国卷Ⅱ)如图，长方体10，AA 1＝8，点E ，F 4.过点E ，F 的平面的面相交，交线围成一个正方形．，垂足为M ，则AM ＝A 1E 为正方形，所以EH ＝EF ＝2-EM 2＝6，AH ＝10，HB 因为长方体被平面α分成两个高为所以其体积的比值为97⎝ ⎛⎭⎪⎫79也正确.一个几何体的三视图如图所示，从上到下由四个简单几何体组成，其体积分别记为，上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有( )4<V 3 B ．V 1<V 3<V 23<V 4D ．V 2<V 3<V 1解：由已知条件及三视图可知，该几何体从上到下依次是圆台，圆柱，正方体，棱台，则V 1＝4π)＝7π3，V 2＝π×12×2＝1×(4＋4×16＋16)＝283.综上可知，。

第八章立体几何第五节直线、平面垂直的判定与性质考点3 线面角、二面角的求法（2018·浙江卷）已知四棱锥S－ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点），设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S－AB－C的平面角为θ3，则（）A．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1【解析】如图，不妨设底面正方形的边长为2，E为AB上靠近点A的四等分点，E′为AB的中点，S到底面的距离SO＝1，以EE′，E′O为邻边作矩形OO′EE′，则∠SEO′＝θ1，∠SEO＝θ2，∠SE′O＝θ3.由题意，得tan θ1＝SO′EO′＝√52，tan θ2＝SOEO ＝√52＝√5，tan θ3＝1，此时tan θ2＜tan θ3＜tan θ1，可得θ2＜θ3＜θ1.当E在AB中点处时，θ2＝θ3＝θ1.故选D．【答案】D（2018·浙江卷）如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC＝120°，A1A ＝4，C1C＝1，AB＝BC＝B1B＝2.（1）证明：AB 1⊥平面A 1B 1C 1；（2）求直线AC 1与平面ABB 1所成的角的正弦值．【解析】方法一 （1）证明 由AB ＝2，AA 1＝4，BB 1＝2，AA 1⊥AB ，BB 1⊥AB ，得AB 1＝A 1B 1＝2√2，所以A 1B 12＋A B 12＝A A 12，故AB 1⊥A 1B 1.由BC ＝2，BB 1＝2，CC 1＝1，BB 1⊥BC ，CC 1⊥BC ，得B 1C 1＝√5.由AB ＝BC ＝2，∠ABC ＝120°，得AC ＝2√3.由CC 1⊥AC ，得AC 1＝√13，所以A B 12＋B 1C 12＝A C 12，故AB 1⊥B 1C 1.又因为A 1B 1∩B 1C 1＝B 1，A 1B 1，B 1C 1⊂平面A 1B 1C 1，因此AB 1⊥平面A 1B 1C 1.（2）如图，过点C 1作C 1D ⊥A 1B 1，交直线A 1B 1于点D ，连接AD ．由AB 1⊥平面A 1B 1C 1，得平面A 1B 1C 1⊥平面ABB 1.由C 1D ⊥A 1B 1，平面A 1B 1C 1∩平面ABB 1＝A 1B 1，C 1D ⊂平面A 1B 1C 1，得C 1D ⊥平面ABB 1.所以∠C 1AD 是AC 1与平面ABB 1所成的角．由B 1C 1＝√5，A 1B 1＝2√2，A 1C 1＝√21，得cos ∠C 1A 1B 1＝√427，sin ∠C 1A 1B 1＝√77，所以C 1D ＝√3，故sin ∠C 1AD ＝C 1DAC 1＝√3913. 因此直线AC 1与平面ABB 1所成的角的正弦值是√3913.方法二 （1）证明 如图，以AC 的中点O 为原点，分别以射线OB ，OC 为x ，y 轴的正半轴，建立空间直角坐标系Oxyz .由题意知各点坐标如下：A （0，－√3，0），B （1,0,0），A 1（0，－√3，4），B 1（1,0,2），C 1（0，√3，1）．因此AB 1⃗⃗⃗⃗⃗⃗⃗ ＝（1，√3，2），A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝（1，√3，－2），A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝（0,2√3，－3）． 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝0，得AB 1⊥A 1B 1.由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ＝0，得AB 1⊥A 1C 1.又A 1B 1∩A 1C 1＝A 1，A 1B 1，A 1C 1⊂平面A 1B 1C 1，所以AB 1⊥平面A 1B 1C 1.（2）设直线AC 1与平面ABB 1所成的角为θ.由（1）可知AC 1⃗⃗⃗⃗⃗⃗⃗ ＝（0,2√3，1），AB ⃗⃗⃗⃗⃗ ＝（1，√3，0），BB 1⃗⃗⃗⃗⃗⃗⃗ ＝（0,0,2）． 设平面ABB 1的一个法向量为n ＝（x ，y ，z ）．由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0, 可取n ＝（－√3，1,0）．所以sin θ＝|cos 〈AC 1⃗⃗⃗⃗⃗⃗⃗ ，n 〉|＝|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n|＝√3913. 因此直线AC 1与平面ABB 1所成的角的正弦值是√3913.【答案】见解析（2018·天津卷（文））如图，在四面体ABCD 中，△ABC 是等边三角形，平面ABC ⊥平面ABD ，点M 为棱AB 的中点，AB ＝2，AD ＝2√3，∠BAD ＝90°.（1）求证：AD ⊥BC ；（2）求异面直线BC 与MD 所成角的余弦值；（3）求直线CD 与平面ABD 所成角的正弦值．【解析】（1）证明 由平面ABC ⊥平面ABD ，平面ABC ∩平面ABD ＝AB ，AD ⊥AB ，AD ⊂平面ABD ，可得AD ⊥平面ABC ，故AD ⊥BC ．（2）如图，取棱AC 的中点N ，连接MN ，ND ．因为M 为棱AB 的中点，所以MN ∥BC ．所以∠DMN （或其补角）为异面直线BC 与MD 所成的角．在Rt △DAM 中，AM ＝1，故DM ＝√AD 2+AM 2＝√13.因为AD ⊥平面ABC ，所以AD ⊥AC ．在Rt △DAN 中，AN ＝1，故DN ＝√AD 2+AN 2＝√13.在等腰三角形DMN 中，MN ＝1，可得cos ∠DMN ＝12MN DM ＝√1326.所以异面直线BC 与MD 所成角的余弦值为√1326. （3）如图，连接CM .因为△ABC 为等边三角形，M 为边AB 的中点，所以CM ⊥AB ，CM ＝√3.又因为平面ABC ⊥平面ABD ，平面ABC ∩平面ABD ＝AB ，而CM ⊂平面ABC ，故CM ⊥平面ABD ，所以∠CDM 为直线CD 与平面ABD 所成的角．在Rt △CAD 中，CD ＝√AC 2+AD 2＝4.在Rt △CMD 中，sin ∠CDM ＝CM CD ＝√34.所以直线CD 与平面ABD 所成角的正弦值为√34.【答案】见解析。

G单元立体几何G1 空间几何体的结构5.G1[2018·全国卷Ⅰ]已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为()A. 12√2πB. 12πC. 8√2πD. 10π5.B[解析] 因为圆柱的轴截面是正方形,且面积为8,所以圆柱的高为2√2,底面直径为2√2,所以圆柱的表面积S=2π×√2×2√2+2×π×(√2)2=12π.故选B.16.G1[2018·全国卷Ⅱ]已知圆锥的顶点为S,母线SA,SB互相垂直,SA与圆锥底面所成角为30°.若△SAB的面积为8,则该圆锥的体积为.16.8π[解析] 如图所示,设圆锥的底面圆的圆心为O,母线长为l,则1l2=8,解得l=4,即SA=4.2连接OS,OA,因为SA与圆锥底面所成的角为30°,所以SO=2.在直角三角形SOA 中,AO=√SA2-SO2=√42-22=2√3,所以圆锥的体积V=1×π×(2√3)2×2=8π.3G2 空间几何体的三视图和直观图9.G2[2018·全国卷Ⅰ]某圆柱的高为2,底面周长为16,其三视图如图1-2所示.圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为()图1-2A. 2√17B. 2√5C. 3D. 29.B[解析] 由三视图可知圆柱表面上点M,N的位置如图①,将圆柱的侧面展开得到图②.在圆柱侧面上,从M到N的路径中,最短路径即为侧面展开图中的线段MN ,MN=√22+(164)2=2√5,故选B .3.G2[2018·全国卷Ⅲ] 中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图1-1中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )图1-1图1-23.A [解析] 卯眼的空间立体图如图,同时需要注意在三视图中,看不见的线用虚线表示,故选A .3.G2[2018·全国卷Ⅲ] 中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图1-1中木构件右边的小长方体是榫头,若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )图1-1图1-23.A[解析] 卯眼的空间立体图如图,同时需要注意在三视图中,看不见的线用虚线表示,故选A.3.G2[2018·浙江卷]某几何体的三视图如图1-1所示(单位:cm),则该几何体的体积(单位:cm3)是()图1-1A. 2B. 4C. 6D. 83.C[解析] 该几何体为直四棱柱,如图所示,底面是直角梯形,其面积为1×(1+2)×2=3,又四棱2柱的高为2,故体积为2×3=6,故选C.G3 平面的基本性质、空间两条直线17.G3、G5[2018·天津卷] 如图1-4,在四面体ABCD 中,△ABC 是等边三角形,平面ABC ⊥平面ABD ,点M 为棱AB 的中点,AB=2,AD=2√3,∠BAD=90°. (1)求证:AD ⊥BC ;(2)求异面直线BC 与MD 所成角的余弦值; (3)求直线CD 与平面ABD 所成角的正弦值.图1-417.解:(1)证明:由平面ABC ⊥平面ABD ,平面ABC ∩平面ABD=AB ,AD ⊥AB ,可得AD ⊥平面ABC ,故AD ⊥BC.(2)取棱AC 的中点N ,连接MN ,ND. 因为M 为棱AB 的中点,故MN ∥BC ,所以∠DMN (或其补角)为异面直线BC 与MD 所成的角. 在Rt △DAM 中,AM=1,故DM=√AD 2+AM 2=√13. 因为AD ⊥平面ABC ,故AD ⊥AC.在Rt △DAN 中,AN=1,故DN=√AD 2+AN 2=√13. 在等腰三角形DMN 中,MN=1,可得cos ∠DMN=12MN DM=√1326. 所以,异面直线BC 与MD 所成角的余弦值为√1326.(3)连接CM.因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM=√3. 又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD , 所以,∠CDM 为直线CD 与平面ABD 所成的角.在Rt△CAD中,CD=√AC2+AD2=4.在Rt△CMD中,sin∠CDM=CMCD =√34.所以,直线CD与平面ABD所成角的正弦值为√34.G4 空间中的平行关系19.G5,G4[2018·全国卷Ⅲ]如图1-5,矩形ABCD所在平面与半圆弧CD⏜所在平面垂直,M是CD⏜上异于C,D的点.(1)证明:平面AMD⊥平面BMC.(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.图1-519.解:(1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.因为M为CD⏜上异于C,D的点,且DC为直径,所以DM⊥CM.又BC∩CM=C,所以DM⊥平面BMC.而DM⊂平面AMD,故平面AMD⊥平面BMC.(2)当P为AM的中点时,MC∥平面PBD.证明如下:连接AC交BD于O.因为四边形ABCD为矩形,所以O为AC中点.连接OP,因为P 为AM中点,所以MC∥OP.MC⊄平面PBD,OP⊂平面PBD,所以MC∥平面PBD.6.G4[2018·浙江卷]已知平面α,直线m,n满足mα,nα,则“m∥n”是“m∥α”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件6.A[解析] 因为m在平面α外,n在平面α内,所以若m∥n,则m∥α;反之,若m∥α,则m和n 可能平行或异面.故“m∥n”是“m∥α”的充分不必要条件,故选A.15.G4,G5[2018·江苏卷]在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.图1-415.证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.18.G4、G5[2018·北京卷]如图1-4,在四棱锥P-ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A⊥PD,P A=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面P AB⊥平面PCD;(3)求证:EF∥平面PCD.图1-418.证明:(1)∵P A=PD,且E为AD的中点,∴PE⊥AD.∵底面ABCD为矩形,∴BC∥AD,∴PE⊥BC.(2)∵底面ABCD为矩形,∴AB⊥AD.∵平面P AD⊥平面ABCD,∴AB⊥平面P AD,∴AB⊥PD.又P A⊥PD,∴PD⊥平面P AB,∴平面P AB⊥平面PCD.(3)如图,取PC的中点G,连接FG,GD.∵F,G分别为PB和PC的中点,∴FG∥BC且FG=1BC.2∵四边形ABCD为矩形,且E为AD的中点,∴ED∥BC,ED=1BC,2∴ED∥FG且ED=FG,∴四边形EFGD为平行四边形,∴EF∥GD.又EF⊄平面PCD,GD⊂平面PCD,∴EF∥平面PCD.G5 空间中的垂直关系18.G5,G12[2018·全国卷Ⅰ]如图1-3所示,在平行四边形ABCM中,AB=AC=3,∠ACM=90°.以AC为折痕将△ACM折起,使点M到达点D的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC;(2)Q为线段AD上一点,P为线段BC上一点,且BP=DQ=2DA,求三棱锥Q-ABP的体积.3图1-318.解:(1)证明:由已知可得,∠BAC=90°,BA ⊥AC. 又BA ⊥AD ,所以AB ⊥平面ACD.又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC. (2)由已知可得,DC=CM=AB=3,DA=3√2. 又BP=DQ=23DA ,所以BP=2√2. 作QE ⊥AC ,垂足为E ,则QE 13DC.由已知及(1)可知DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE=1.因此,三棱锥Q - ABP 的体积为V Q - ABP =13×QE×S △ABP =13×1×12×3×2√2sin 45°=1.19.G5,G12[2018·全国卷Ⅱ] 如图1-4,在三棱锥P-ABC 中,AB=BC=2√2,P A=PB=PC=AC=4,O 为AC 的中点.图1-4(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC=2MB ,求点C 到平面POM 的距离.19.解:(1)证明:因为AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2√3. 连接OB.因为AB=BC=√22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB=12AC=2. 由OP 2+OB 2=PB 2知,OP ⊥OB.由OP ⊥OB ,OP ⊥AC ,OB ∩AC=O 知PO ⊥平面ABC.(2)作CH ⊥OM ,垂足为H ,又由(1)可得OP ⊥CH ,OP ∩OM=O ,所以CH ⊥平面POM , 故CH 的长为点C 到平面POM 的距离. 由题设可知OC=12AC=2,CM=23BC=4√23,∠ACB=45°, 所以OM=2√53,CH=OC ·MC ·sin ∠ACB OM=4√55, 所以点C 到平面POM 的距离为4√55.19.G5,G4[2018·全国卷Ⅲ] 如图1-5,矩形ABCD 所在平面与半圆弧CD ⏜所在平面垂直,M 是CD ⏜上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC.(2)在线段AM 上是否存在点P ,使得MC ∥平面PBD ?说明理由.图1-519.解:(1)证明:由题设知,平面CMD ⊥平面ABCD ,交线为CD.因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM.因为M 为CD⏜上异于C ,D 的点,且DC 为直径,所以DM ⊥CM. 又BC ∩CM=C ,所以DM ⊥平面BMC. 而DM ⊂平面AMD ,故平面AMD ⊥平面BMC. (2)当P 为AM 的中点时,MC ∥平面PBD.证明如下:连接AC 交BD 于O.因为四边形ABCD 为矩形,所以O 为AC 中点.连接OP ,因为P 为AM 中点,所以MC ∥OP .MC ⊄平面PBD ,OP ⊂平面PBD ,所以MC ∥平面PBD.19.G5,G11,G12[2018·浙江卷]如图1-3所示,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.图1-3(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.19.解: 方法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2√2,所以A1B12+A B12=A A12, 故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=√5,由AB=BC=2,∠ABC=120°得AC=2√3,由CC1⊥AC,得AC1=√13,所以A B12+B1C12=A C12,故AB1⊥B1C1.因此AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,由C1D⊥A1B1得C1D⊥平面ABB1,所以∠C1AD是AC1与平面ABB1所成的角.由B1C1=√5,A1B1=2√2,A1C1=√21得cos ∠C 1A 1B 1=√6√7,sin ∠C 1A 1B 1=√7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 15.G4,G5[2018·江苏卷] 在平行六面体ABCD - A 1B 1C 1D 1中,AA 1=AB ,AB 1⊥B 1C 1. 求证:(1)AB ∥平面A 1B 1C ; (2)平面ABB 1A 1⊥平面A 1BC.图1-415.证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,因此AB1⊥A1B.又因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC.因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.18.G4、G5[2018·北京卷]如图1-4,在四棱锥P-ABCD中,底面ABCD为矩形,平面P AD⊥平面ABCD,P A⊥PD,P A=PD,E,F分别为AD,PB的中点.(1)求证:PE⊥BC;(2)求证:平面P AB⊥平面PCD;(3)求证:EF∥平面PCD.图1-418.证明:(1)∵P A=PD,且E为AD的中点,∴PE⊥AD.∵底面ABCD为矩形,∴BC∥AD,∴PE⊥BC.(2)∵底面ABCD为矩形,∴AB⊥AD.∵平面P AD⊥平面ABCD,∴AB⊥平面P AD,∴AB⊥PD.又P A⊥PD,∴PD⊥平面P AB,∴平面P AB⊥平面PCD.(3)如图,取PC的中点G,连接FG,GD.∵F,G分别为PB和PC的中点,∴FG∥BC且FG=1BC.2∵四边形ABCD为矩形,且E为AD的中点,∴ED∥BC,ED=1BC,2∴ED∥FG且ED=FG,∴四边形EFGD为平行四边形,∴EF∥GD.又EF⊄平面PCD,GD⊂平面PCD,∴EF∥平面PCD.17.G3、G5[2018·天津卷]如图1-4,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=2√3,∠BAD=90°.(1)求证:AD⊥BC;(2)求异面直线BC与MD所成角的余弦值;(3)求直线CD与平面ABD所成角的正弦值.图1-417.解:(1)证明:由平面ABC⊥平面ABD,平面ABC∩平面ABD=AB,AD⊥AB,可得AD⊥平面ABC,故AD⊥BC.(2)取棱AC的中点N,连接MN,ND.因为M为棱AB的中点,故MN∥BC,所以∠DMN(或其补角)为异面直线BC与MD所成的角.在Rt△DAM中,AM=1,故DM=√AD2+AM2=√13.因为AD⊥平面ABC,故AD⊥AC.在Rt△DAN中,AN=1,故DN=√AD2+AN2=√13.在等腰三角形DMN 中,MN=1,可得cos ∠DMN=12MN DM =√1326. 所以,异面直线BC 与MD 所成角的余弦值为√1326.(3)连接CM.因为△ABC 为等边三角形,M 为边AB 的中点,故CM ⊥AB ,CM=√3. 又因为平面ABC ⊥平面ABD ,而CM ⊂平面ABC ,故CM ⊥平面ABD , 所以,∠CDM 为直线CD 与平面ABD 所成的角. 在Rt △CAD 中,CD=√AC 2+AD 2=4. 在Rt △CMD 中,sin ∠CDM=CM CD =√34. 所以,直线CD 与平面ABD 所成角的正弦值为√34.G6 三垂线定理 G7 棱柱与棱锥11.G7[2018·天津卷] 如图1-3,已知正方体ABCD - A 1B 1C 1D 1的棱长为1,则四棱锥A 1 - BB 1D 1D 的体积为 .图1-311.13 [解析] 点A 1到平面BB 1D 1D 的距离为√22,四边形BB 1D 1D 的面积为√2,故四棱锥A 1 - BB 1D 1D 的体积为13×√2×√22=13.G8 多面体与球12.G8[2018·全国卷Ⅲ] 设A ,B ,C ,D 是同一个半径为4的球的球面上四点,△ABC 为等边三角形且其面积为9√3,则三棱锥D-ABC 体积的最大值为( )A .12√3B .18√3C.24√3D.54√312.B[解析] 由题易知当点D到平面ABC的距离最大时,三棱锥D-ABC的体积最大.∵S△ABC=√34AB2=9√3,∴AB=6.设△ABC的中心为M,由等边三角形的性质得,AM=BM=CM=2√3.设球心为O,则OA=OB=OC=4,∴OM=√OB2-BM2=2,∴点D到平面ABC的距离的最大值为OM+4=6.故三棱锥D-ABC体积的最大值为13×9√3×6=18√3.G9空间向量及运算G10 空间向量解决线面位置关系G11 空间角与距离的求法9.G11[2018·全国卷Ⅱ]在正方体ABCD-A1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD 所成角的正切值为()A. √22B. √32C. √52D. √729.C[解析] 如图,由AB∥CD,可知∠BAE即为异面直线AE与CD所成的角.设正方体的棱长为2,连接BE,则在Rt△ABE中,AB=2,BE=√BC2+CE2=√22+12=√5,tan∠BAE=BEAB =√52,故选C.8.G11[2018·浙江卷]已知四棱锥S-ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点).设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S-AB-C的平面角为θ3,则()A.θ1≤θ2≤θ3B.θ3≤θ2≤θ1C.θ1≤θ3≤θ2D.θ2≤θ3≤θ18.D[解析] 过S作SO⊥平面ABCD,连接OE,则θ2=∠SEO,sin θ2=SOSE.取AB的中点F,连接OF,则θ3=∠SFO,sin θ3=SOSF ,∵SE≥SF,∴sin θ2≤sin θ3,又θ2,θ3∈(0,π2),∴θ2≤θ3.作GE∥BC,OG⊥GE,连接SG,则GE⊥SG,θ1=∠SEG,tan θ1=SGGE ,∵OF=GE,SO≤SG,tan θ3=SOOF,∴tanθ3≤tan θ1,∴θ2≤θ3≤θ1,故选D.19.G55,G11,G12[2018·浙江卷]如图1-3所示,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.图1-3(1)证明:AB1⊥平面A1B1C1;(2)求直线AC1与平面ABB1所成的角的正弦值.19.解: 方法一:(1)证明:由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=2√2,所以A1B12+A B12=A A12, 故AB1⊥A1B1.由BC=2,BB1=2,CC1=1,BB1⊥BC,CC1⊥BC得B1C1=√5,由AB=BC=2,∠ABC=120°得AC=2√3,由CC1⊥AC,得AC1=√13,所以A B12+B1C12=A C12,故AB1⊥B1C1.因此AB1⊥平面A1B1C1.(2)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连接AD.由AB 1⊥平面A 1B 1C 1得平面A 1B 1C 1⊥平面ABB 1, 由C 1D ⊥A 1B 1得C 1D ⊥平面ABB 1, 所以∠C 1AD 是AC 1与平面ABB 1所成的角. 由B 1C 1=√5,A 1B 1=2√2,A 1C 1=√21得 cos ∠C 1A 1B 1=√67,sin ∠C 1A 1B 1=7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913.因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 22.G11[2018·江苏卷] 如图1-8所示,在正三棱柱ABC - A 1B 1C 1中,AB=AA 1=2,点P ,Q 分别为A 1B 1,BC 的中点.(1)求异面直线BP 与AC 1所成角的余弦值; (2)求直线CC 1与平面AQC 1所成角的正弦值.图1-822.解:如图,在正三棱柱ABC - A 1B 1C 1中,设AC ,A 1C 1的中点分别为O ,O 1,则OB ⊥OC ,OO 1⊥OC ,OO 1⊥OB ,以{OB ⃗⃗⃗⃗⃗ ,OC ⃗⃗⃗⃗ ,OO 1⃗⃗⃗⃗⃗⃗⃗ }为基底,建立空间直角坐标系O - xyz. 因为AB=AA 1=2,所以A (0,-1,0),B (√3,0,0),C (0,1,0),A 1(0,-1,2),B 1(√3,0,2),C 1(0,1,2).(1)因为P 为A 1B 1的中点,所以P √32,-12,2,从而BP ⃗⃗⃗⃗⃗ =-√32,-12,2,AC 1⃗⃗⃗⃗⃗⃗ =(0,2,2), 故|cos <BP ⃗⃗⃗⃗⃗ ,AC 1⃗⃗⃗⃗⃗⃗ >|=|BP ⃗⃗⃗⃗⃗⃗ ·AC1⃗⃗⃗⃗⃗⃗⃗⃗⃗ ||BP ⃗⃗⃗⃗⃗⃗ |·|AC1⃗⃗⃗⃗⃗⃗⃗⃗⃗ |=√5×2√2=3√1020. 因此,异面直线BP 与AC 1所成角的余弦值为3√1020. (2)因为Q 为BC 的中点,所以Q√32,12,0,因此AQ⃗⃗⃗⃗⃗ =√32,32,0,AC 1⃗⃗⃗⃗⃗⃗ =(0,2,2),CC 1⃗⃗⃗⃗⃗⃗ =(0,0,2).设n=(x ,y ,z )为平面AQC 1的一个法向量,则{AQ ⃗⃗⃗⃗⃗ ·n =0,AC 1⃗⃗⃗⃗⃗⃗⃗ ·n =0,即{√32x +32y =0,2y +2z =0. 不妨取n=(√3,-1,1),设直线CC 1与平面AQC 1所成的角为θ,则sin θ=|cos <CC 1⃗⃗⃗⃗⃗⃗ ,n>|=|CC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||CC 1⃗⃗⃗⃗⃗⃗⃗⃗|·|n|=√5×2=√55, 所以直线CC 1与平面AQC 1所成角的正弦值为√55.G12 单元综合10.G12[2018·全国卷Ⅰ] 在长方体ABCD - A 1B 1C 1D 1中,AB=BC=2,AC 1与平面BB 1C 1C 所成的角为30°,则该长方体的体积为 ( ) A . 8 B . 6√2 C . 8√2D . 8√310.C [解析] 如图,连接BC 1,易知∠AC 1B 即为AC 1与平面BB 1C 1C 所成的角,由题易知∠AC 1B=30°,易得AC 1=2AB=4.设BB 1=h ,则有42=22+22+h 2, 解得h=2√2,所以该长方体的体积V=2×2×2√2=8√2.18.G5,G12[2018·全国卷Ⅰ] 如图1-3所示,在平行四边形ABCM 中,AB=AC=3,∠ACM=90°.以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB ⊥DA. (1)证明:平面ACD ⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且BP=DQ=23DA ,求三棱锥Q - ABP 的体积.图1-318.解:(1)证明:由已知可得,∠BAC=90°,BA ⊥AC. 又BA ⊥AD ,所以AB ⊥平面ACD.又AB ⊂平面ABC ,所以平面ACD ⊥平面ABC. (2)由已知可得,DC=CM=AB=3,DA=3√2. 又BP=DQ=23DA ,所以BP=2√2. 作QE ⊥AC ,垂足为E ,则QE 13DC.由已知及(1)可知DC ⊥平面ABC ,所以QE ⊥平面ABC ,QE=1.因此,三棱锥Q - ABP 的体积为V Q - ABP =13×QE×S △ABP =13×1×12×3×2√2sin 45°=1.19.G5,G12[2018·全国卷Ⅱ] 如图1-4,在三棱锥P-ABC 中,AB=BC=2√2,P A=PB=PC=AC=4,O 为AC 的中点.图1-4(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且MC=2MB ,求点C 到平面POM 的距离.19.解:(1)证明:因为AP=CP=AC=4,O 为AC 的中点,所以OP ⊥AC ,且OP=2√3. 连接OB.因为AB=BC=√22AC ,所以△ABC 为等腰直角三角形,且OB ⊥AC ,OB=12AC=2.由OP 2+OB 2=PB 2知,OP ⊥OB.由OP ⊥OB ,OP ⊥AC ,OB ∩AC=O 知PO ⊥平面ABC.(2)作CH ⊥OM ,垂足为H ,又由(1)可得OP ⊥CH ,OP ∩OM=O ,所以CH ⊥平面POM , 故CH 的长为点C 到平面POM 的距离. 由题设可知OC=12AC=2,CM=23BC=4√23,∠ACB=45°, 所以OM=2√53,CH=OC ·MC ·sin ∠ACB OM=4√55, 所以点C 到平面POM 的距离为4√55.19.G55,G11,G12[2018·浙江卷] 如图1-3所示,已知多面体ABCA 1B 1C 1,A 1A ,B 1B ,C 1C 均垂直于平面ABC ,∠ABC=120°,A 1A=4,C 1C=1,AB=BC=B 1B=2.图1-3(1)证明:AB 1⊥平面A 1B 1C 1;(2)求直线AC 1与平面ABB 1所成的角的正弦值. 19.解: 方法一:(1)证明:由AB=2,AA 1=4,BB 1=2,AA 1⊥AB ,BB 1⊥AB 得AB 1=A 1B 1=2√2,所以A 1B 12+A B 12=A A 12,故AB 1⊥A 1B 1.由BC=2,BB 1=2,CC 1=1,BB 1⊥BC ,CC 1⊥BC 得B 1C 1=√5, 由AB=BC=2,∠ABC=120°得AC=2√3,由CC 1⊥AC ,得AC 1=√13,所以A B 12+B 1C 12=A C 12,故AB 1⊥B 1C 1.因此AB 1⊥平面A 1B 1C 1.(2)如图,过点C 1作C 1D ⊥A 1B 1,交直线A 1B 1于点D ,连接AD.由AB 1⊥平面A 1B 1C 1得平面A 1B 1C 1⊥平面ABB 1, 由C 1D ⊥A 1B 1得C 1D ⊥平面ABB 1, 所以∠C 1AD 是AC 1与平面ABB 1所成的角. 由B 1C 1=√5,A 1B 1=2√2,A 1C 1=√21得 cos ∠C 1A 1B 1=√67,sin ∠C 1A 1B 1=7,所以C 1D=√3,故sin ∠C 1AD=C 1D AC 1=√3913.因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 方法二:(1)证明:如图,以AC 的中点O 为原点,分别以射线OB ,OC 为x ,y 轴的正半轴,建立空间直角坐标系O-xyz.由题意知,各点坐标如下:A (0,-√3,0),B (1,0,0),A 1(0,-√3,4),B 1(1,0,2),C 1(0,√3,1). 因此AB 1⃗⃗⃗⃗⃗⃗⃗ =(1,√3,2),A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(1,√3,-2),A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,-3). 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1B 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1B 1. 由AB 1⃗⃗⃗⃗⃗⃗⃗ ·A 1C 1⃗⃗⃗⃗⃗⃗⃗⃗⃗ =0得AB 1⊥A 1C 1. 所以AB 1⊥平面A 1B 1C 1.(2)设直线AC 1与平面ABB 1所成的角为θ. 由(1)可知AC 1⃗⃗⃗⃗⃗⃗⃗ =(0,2√3,1),AB ⃗⃗⃗⃗⃗ =(1,√3,0),BB 1⃗⃗⃗⃗⃗⃗⃗ =(0,0,2). 设平面ABB 1的法向量n=(x ,y ,z ).由{n ·AB ⃗⃗⃗⃗⃗ =0,n ·BB 1⃗⃗⃗⃗⃗⃗⃗ =0,得{x +√3y =0,2z =0,可取n=(-√3,1,0).所以sin θ=|cos <AC 1⃗⃗⃗⃗⃗⃗⃗ ,n>|=|AC 1⃗⃗⃗⃗⃗⃗⃗⃗ ·n||AC 1⃗⃗⃗⃗⃗⃗⃗⃗ |·|n|=√3913. 因此,直线AC 1与平面ABB 1所成的角的正弦值是√3913. 10.G12[2018·江苏卷] 如图1-3所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为 .图1-310.43 [解析] 该几何体是一个正八面体,而正八面体是由两个相同的正四棱锥组成的,由图可知一个正四棱锥的高为1,底面边长为12√22+22=√2,所以正八面体的体积V=2×13×(√2)2×1=43.1.[2018·衡阳八中月考] 如图K31-3,ABCD -A 1B 1C 1D 1为正方体,给出下列结论:①BD ∥平面CB 1D 1;②AC 1⊥BD ;③AC 1⊥平面CB 1D 1;④B 1D 1与BC 所成的角为45°.其中正确结论的个数是( )A .1B .2C .3D .4图K31-3图K31-41.D[解析]对于①,由正方体的性质得BD∥B1D1,所以BD∥平面CB1D1,故①中结论正确;对于②,连接AC,由正方体的性质得AC⊥BD,而AC是AC1在底面ABCD内的投影,可得AC1⊥BD,故②中结论正确;对于③,由正方体的性质得BD∥B1D1,由②知AC1⊥BD,所以AC1⊥B1D1,同理可证AC1⊥CB1,故AC1垂直于平面CB1D1内的两条相交直线,所以AC1⊥平面CB1D1,故③中结论正确;对于④,异面直线B1D1与BC所成的角就是直线BC与BD所成的角,故∠CBD即为异面直线B1D1与BC所成的角,在等腰直角三角形BCD中,∠CBD=45°,故B1D1与BC所成的角为45°,故④中结论正确.故选D.2.[2018·桂林、百色、梧州、崇左、北海五市联合模拟]如图K33-11,在正三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,且EC=2FB.(1)证明:平面AEF⊥平面ACC1A1;(2)若AB=EC=2,求三棱锥C-AEF的体积.图K33-11EC=BF,又2.解:(1)证明:取线段AE的中点G,线段AC的中点M,连接MG,GF,BM,则MG=12MG∥EC∥BF,∴四边形MBFG是平行四边形,故MB∥FG.∵△ABC为正三角形,M为AC的中点,∴MB⊥AC,又平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,∴MB⊥平面ACC1A1,而MB∥FG,∴FG⊥平面ACC1A1,又∵FG⊂平面AEF,∴平面AEF⊥平面ACC1A1.(2)由(1)得FG⊥平面AEC,FG=BM=√3,所以VCAEF =VFACE=13×S△ACE·FG=13×12×2×2×√3=2√33.3.[2018·石家庄质检]如图K32-9,在四棱锥P-ABCD中,底面ABCD为正方形,且PA⊥底面ABCD,过AB的平面与侧面PCD的交线为EF,且满足S△PEF∶S四边形CDEF=1∶3(S△PEF表示△PEF的面积).(1)证明:PB∥平面ACE;(2)当PA=2AD=2时,求点F到平面ACE的距离.图K32-93.解:(1)证明:由题知四边形ABCD为正方形,∴AB∥CD,又CD⊂平面PCD,AB⊄平面PCD,∴AB∥平面PCD,又AB⊂平面ABFE,平面ABFE∩平面PCD=EF,∴EF∥AB,又AB∥CD,∴EF∥CD.又由S△PEF∶S四边形CDEF=1∶3知E,F分别为PD,PC的中点.连接BD交AC 与点G,则G为BD的中点.连接EG,在△PBD中,EG为中位线,∴EG∥PB.∵EG⊂平面ACE,PB⊄平面ACE,∴PB∥平面ACE.(2)连接AF .∵P A=2,AD=AB=1,∴AC=√2,AE=12PD=√52.∵CD ⊥AD ,CD ⊥P A ,AD ∩P A=A ,∴CD ⊥平面P AD ,∴CD ⊥PD.在Rt △CDE 中,CE=√CD 2+DE 2=32.在△ACE 中,由余弦定理知cos ∠AEC=AE 2+CE 2-AC 22AE ·CE =√55,∴sin ∠AEC=2√55,∴S △ACE =12AE ·CE ·sin ∠AEC=34.设点F 到平面ACE 的距离为h ,则V FACE =13×34×h=14h.由DG ⊥AC ,DG ⊥P A ,AC ∩P A=A ,得DG ⊥平面P AC ,且DG=√22.∵E 为PD 的中点,∴E 到平面ACF 的距离为12DG=√24,又F 为PC 的中点,∴S △ACF =12S △ACP =√22,∴V EACF =13×√22×√24=112.由V FACE =V EACF 知h=13,∴点F 到平面ACE 的距离为13.。