模态测试与分析基本概念

模态分析模态分析模态分析是研究结构动⼒特性⼀种⽅法，⼀般应⽤在⼯程振动领域。

其中，模态是指机械结构的固有振动特性，每⼀个模态都有特定的固有频率、阻尼⽐和模态振型。

分析这些模态参数的过程称为模态分析。

由有限元计算的⽅法取得——计算模态分析；通过试验将采集的系统输⼊与输出信号经过参数识别获得——试验模态分析。

通常，模态分析都是指试验模态分析。

概述振动模态是弹性结构固有的、整体的特性。

通过模态分析⽅法搞清楚了结构物在某⼀易受影响的频率范围内的各阶主要模态的特性，就可以预⾔结构在此频段内在外部或内部各种振源作⽤下产⽣的实际振动响应。

因此，模态分析是结构动态设计及设备故障诊断的重要⽅法。

机器、建筑物、航天航空飞⾏器、船舶、汽车等的实际振动模态各不相同。

模态分析提供了研究各类振动特性的⼀条有效途径。

⾸先，将结构物在静⽌状态下进⾏⼈为激振，通过测量激振⼒与响应并进⾏双通道快速傅⾥叶变换（FFT）分析，得到任意两点之间的机械导纳函数（传递函数）。

⽤模态分析理论通过对试验导纳函数的曲线拟合，识别出结构物的模态参数，从⽽建⽴起结构物的模态模型。

根据模态叠加原理，在已知各种载荷时间历程的情况下，就可以预⾔结构物的实际振动的响应历程或响应谱。

近⼗多年来，由于计算机技术、FFT分析仪、⾼速数据采集系统以及振动传感器、激励器等技术的发展，试验模态分析得到了很快的发展，受到了机械、电⼒、建筑、⽔利、航空、航天等许多产业部门的⾼度重视。

已有多种档次、各种原理的模态分析硬件与软件问世。

模态的阶：如果把这些共振频率都按照频率值从⼩到⼤排，就是“阶”。

每个物体都有⾃⼰的共振频率，⽽且还有不⽌⼀个共振频率。

可能⼗⼏Hz的时候会发⽣共振，⼏百Hz的时候⼜会发⽣共振。

如果进⾏模态分析，就是说把这个物体的共振频率都找出来。

⽐如说最⼩的共振频率就是⼀阶。

为什么⼀般做模态分析,只关注低阶模态,⽽忽略⾼阶模态呢⼀般载荷的频率是⽐较低的，所以只需要考虑与前⼏阶低阶模态是否会共振。

模态测试方面的经典书籍模态测试是软件测试中的一种方法，用于评估软件系统在不同条件下的性能和行为。

以下是关于模态测试方面的经典书籍，它们涵盖了模态测试的基本概念、技术和最佳实践。

1.《模态测试实践指南》（Modal Testing: A Practical Guide）- D. J. Ewins这本书是模态测试领域的经典之作，介绍了模态测试的基本原理、测试方法和数据分析技术。

它详细解释了如何设计和执行模态测试，并提供了实用的案例研究和问题解答。

2.《模态测试与分析》（Modal Testing and Analysis）- A. D. Marinescu这本书介绍了模态测试的理论和实践，包括模态参数的测量和分析、模态试验设计、数据采集与处理等方面的内容。

它深入探讨了模态测试的各个环节，并提供了丰富的案例和实例来帮助读者理解和应用模态测试技术。

3.《振动模态测试与分析》（Vibration Modal Testing and Analysis）-D. J. Ewins这本书介绍了振动模态测试的基本原理和方法，包括模态参数的测量和分析、模态试验设计、数据采集与处理等方面的内容。

它提供了大量的实例和案例，帮助读者理解和应用振动模态测试技术。

4.《模态测试与分析技术》（Modal Testing and Analysis Techniques）- S. N. Sinha这本书详细介绍了模态测试和分析的各个方面，包括模态参数的测量和分析、模态试验设计、数据采集与处理等内容。

它提供了大量的实例和案例，帮助读者理解和应用模态测试技术。

5.《结构动力学与模态测试》（Structural Dynamics and Modal Testing）- J. H. Cannon这本书讲解了结构动力学和模态测试的基本原理和方法，包括结构振动的基本理论、模态参数的测量和分析、模态试验设计、数据采集与处理等内容。

它通过实例和案例来帮助读者理解和应用结构动力学和模态测试技术。

模态分析综述一、前言模态分析是研究结构动力特性的一种近代方法,是系统辨别方法在工程振动领域中的应用。

模态是机械结构的固有振动特性,每一个模态具有特定的固有频率、阻尼比和模态振型。

这些模态参数可以由计算或试验分析取得,这样一个计算或试验分析过程称为模态分析。

振动模态是弹性结构固有的、整体的特性。

如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内,各阶主要模态的特性,就可能预知结构在此频段内,在外部或内部各种振源作用下实际振动响应,而且一旦通过模态分析知道模态参数并给予验证,就可以把这些参数用于(重)设计过程,优化系统动态特性,或者研究把该结构连接到其他结构上时所产生的影响。

因此,模态分析是结构动态设计及设备故障诊断的重要方法。

近十余年以来,模态分析的理论基础,已经由传统的线性位移实模态、复模态理论发展到广义模态理论,并被进一步引入到非线性结构振动分析领域,同时模态分析理论汲取了振动理论、信号分析、数据处理、数理统计以及自动控制的相关理论,结合自身的发展规律,形成了一套独特的理论体系,创造了更加广泛的应用前景。

这一技术已经在航空、航天、造船、机械、建筑、交通运输和兵器等工程领域得到广泛应用。

二、模态分析的定义与用处模态分析的经典定义：将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数。

坐标变换的变换矩阵为模态矩阵，其每列为模态振型。

由振动理论知：一个线性振动系统，当它按自身某一阶固有频率作自由谐振时，整个系统将具有确定的振动形态（简称振型或模态）。

模态是工程结构的固有振动特性，每一个模态具有特定参数，即固有频率、阻尼比和模态振型等。

此外，基于线性叠加原理，一个复杂的振动还可以分解为许多的模态叠加。

一般地，以振动理论为基础、以模态参数为目标的分析方法，称为模态分析。

更确切地说，模态分析是研究系统物理参数模型、模态参数模型和非参数模型的关系，并通过一定手段确定这些系统模型的理论及其应用的一门学科。

你能为我解释模态分析吗？好，需要花费一点时间，但是这是任何人都能明白的事情……你不是第一个要求我用通俗易懂的语言解释模态分析的人，这样一来，任何人都能明白模态分析到底是怎样一个过程。

简单地说，模态分析是根据用结构的固有特征，包括频率、阻尼和模态振型，这些动力学属性去描述结构的过程。

那只是一句总结性的语言，现在让我来解释模态分析到底是怎样的一个过程。

不涉及太多的技术方面的知识，我经常用一块平板的振动模式来简单地解释模态分析。

这个解释过程对于那些振动和模态分析的新手们通常是有用的。

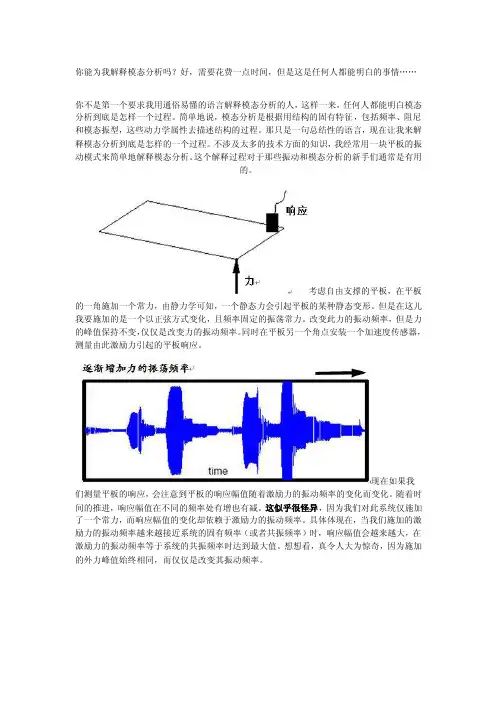
考虑自由支撑的平板，在平板的一角施加一个常力，由静力学可知，一个静态力会引起平板的某种静态变形。

但是在这儿我要施加的是一个以正弦方式变化，且频率固定的振荡常力。

改变此力的振动频率，但是力的峰值保持不变，仅仅是改变力的振动频率。

同时在平板另一个角点安装一个加速度传感器，测量由此激励力引起的平板响应。

现在如果我们测量平板的响应，会注意到平板的响应幅值随着激励力的振动频率的变化而变化。

随着时间的推进，响应幅值在不同的频率处有增也有减。

这似乎很怪异，因为我们对此系统仅施加了一个常力，而响应幅值的变化却依赖于激励力的振动频率。

具体体现在，当我们施加的激励力的振动频率越来越接近系统的固有频率（或者共振频率）时，响应幅值会越来越大，在激励力的振动频率等于系统的共振频率时达到最大值。

想想看，真令人大为惊奇，因为施加的外力峰值始终相同，而仅仅是改变其振动频率。

时域数据提供了非常有用的信息，但是如果用快速傅立叶变换（FFT）将时域数据转换到频域，可以计算出所谓的频响函数（FRF）。

这个函数有一些非常有趣的信息值得关注：注意到频响函数的峰值出现在系统的共振频率处，注意到频响函数的这些峰出现在观测到的时域响应信号的幅值达到最大时刻的频率处。

如果我们将频响函数叠加在时域波形之上，会发现时域波形幅值达到最大值时的激励力振动频率等于频响函数峰值处的频率。

机械结构的振动测试与模态分析机械结构的振动是指在运动或工作过程中，由于受到外界激励或内部失稳因素的影响而出现的周期性或非周期性的振动现象。

振动不仅会影响机械结构的正常运行，还可能导致结构疲劳、损坏，甚至产生严重事故。

因此，了解机械结构的振动特性，进行振动测试和模态分析，对于结构设计、改进和维护具有重要意义。

1. 振动测试振动测试是通过实验手段对机械结构的振动特性进行测量和分析的过程。

常见的振动测试手段包括加速度传感器、速度传感器、位移传感器等。

通过这些传感器，可以测量到结构在不同频率范围内的振动加速度、振动速度和振动位移等参数。

振动测试不仅可以定量地描述结构的振动特性，还可以研究振动的传播路径、频谱特性和共振现象等。

2. 模态分析模态分析是对机械结构的振动特性进行分析和研究的过程。

模态分析的目的是确定结构的振动模态，即结构的固有频率、振型和阻尼等参数。

通过模态分析，可以了解机械结构在不同频率下的振动特性，并确定结构中可能存在的共振点和振动节点。

同时，模态分析还可以帮助设计师优化结构的设计，减小结构的振动幅值，提高结构的工作效率和可靠性。

3. 应用案例以汽车底盘为例，进行振动测试和模态分析的应用。

在汽车行驶过程中，底盘承受着来自路面的冲击和车辆运动的振动。

通过振动测试，可以测量到底盘在不同行驶速度下的振动加速度和振动速度等参数。

通过模态分析，可以确定底盘的固有频率和振型，判断底盘是否在某些特定频率下容易出现共振现象。

根据振动测试和模态分析的结果，可以对底盘的结构进行优化，提高底盘的刚度和减小噪声，提高驾驶的舒适性和汽车的安全性能。

4. 振动测试与模态分析的意义振动测试与模态分析对于机械结构的设计、改进和维护具有重要意义。

通过振动测试，可以了解机械结构在不同工况下的振动特性，及时发现结构的振动异常和故障等。

通过模态分析，可以确定结构的固有频率和振型，为结构的优化设计提供依据。

同时，振动测试与模态分析还可以帮助工程师评估结构的可靠性和耐久性，减小结构的振动幅值，提高结构的工作效率和可靠性。

汽轮发电机定子绕组端部模态测试与分析何青;崔志斌;韩泓池【摘要】汽轮发电机的定子绕组端部在运行中受到旋转电磁力的作用而受迫振动,造成安全隐患.因此,新机出厂或大修时,需对发电机定子绕组端部动态特性做出判断,以便及时排除故障,减少经济损失.以模态分析的试验法为指导,对一台汽轮发电机的定子绕组端部进行测试和试验数据分析,进而得出该发电机励端和汽端的模态振型估计结果.在测试和分析过程中发现:模态置信准则矩阵能够为可能的错误模态估计结果指出思考的方向;不理想的激励信号输入或不理想的响应信号试验数据会降低模态估计结果的精度.【期刊名称】《电力与能源》【年(卷),期】2017(000)004【总页数】5页(P467-471)【关键词】汽轮发电机;定子绕组;模态测试;模态分析;模态置信准则【作者】何青;崔志斌;韩泓池【作者单位】华北电力大学能源动力与机械工程学院,北京 102206;华北电力大学能源动力与机械工程学院,北京 102206;华北电力大学能源动力与机械工程学院,北京 102206【正文语种】中文【中图分类】TM311在汽轮发电机运转发电过程中，定子线圈电流和转子端部的漏磁通彼此作用，定子端部绕组会受到它们之间所产生的旋转电磁力的作用。

定子绕组端部出现的振动问题，从20世纪90年代起，我国对此问题开展了研究。

模态分析是力学结构动力学特征研究的一种手段，模态参数可通过仿真计算或试验数据分析得到。

在汽轮发电机的研发过程中，利用ANSYS等有限元分析软件进行的计算模态分析，能够为定子端部结构设计提供一定的技术支持[1]。

在汽轮发电机新机出厂、交接及检修过程中，试验模态分析能够为其定子端部的动态特性评判提供依据。

基于多年来工程人员的应用经验及研究人员的研究成果，我国于2006年发布了《透平型发电机定子绕组端部动态特性和振动试验方法及评定》的国家标准。

近些年来，测量按国外先进技术制造的1 000 MW汽轮发电机定子端部的动态特征时，仇明等发现了尽管测试结果不与标准要求相符但被测对象并不存在端部故障的情况，并提出了修订标准的建议[2]。

模态分析用于确定设计结构或机器部件的振动特性（固有频率和振型），即结构的固有频率和振型，它们是承受动态载荷结构设计中的重要参数。

同时，也可以作为其它动力学分析问题的起点，例如瞬态动力学分析、谐响应分析和谱分析，其中模态分析也是进行谱分析或模态叠加法谐响应分析或瞬态动力学分析所必需的前期分析过程。

ANSYS的模态分析可以对有预应力的结构进行模态分析和循环对称结构模态分析。

前者有旋转的涡轮叶片等的模态分析，后者则允许在建立一部分循环对称结构的模型来完成对整个结构的模态分析。

ANSYS产品家族中的模态分析是一个线性分析。

任何非线性特性，如塑性和接触（间隙）单元，即使定义了也将被忽略。

ANSYS提供了七种模态提取方法，它们分别是子空间法、分块Lanczos法、PowerDynamics法、缩减法、非对称法、阻尼法和QR阻尼法。

阻尼法和QR阻尼法允许在结构中存在阻尼。

后面将详细介绍模态提取方法。

§1.2模态分析中用到的命令模态分析使用所有其它分析类型相同的命令来建模和进行分析。

同样，无论进行何种类型的分析，均可从用户图形界面（GUI）上选择等效于命令的菜单选项来建模和求解问题。

后面的“模态分析实例（命令流或批处理方式）”将给出进行该实例模态分析时要输入的命令（手工或以批处理方式运行ANSYS时）。

而“模态分析实例（GUI方式）” 则给出了以从ANSYS GUI中选择菜单选项方式进行同一实例分析的步骤。

（要想了解如何使用命令和GUI选项建模，请参阅< <ANSYS建模与网格指南>>）。

<<ANSYS命令参考手册>>中有更详细的按字母顺序列出的ANS YS命令说明。

§1.3模态提取方法典型的无阻尼模态分析求解的基本方程是经典的特征值问题：其中：=刚度矩阵,=第阶模态的振型向量（特征向量）,=第阶模态的固有频率（是特征值）,=质量矩阵。

有许多数值方法可用于求解上面的方程。

模态分析技术⼩节1模态分析⼊门1.1⽬的通过实验模态分析了解结构的动⼒学特性，进⽽修改模型，优化设计基于“⾃激励”的数控装备实验模态分析的新⽅法，直接以系统的⼯作载荷或环境的⾃然扰动作为随机激振源（只要这些振源的宽带⾜以覆盖系统的有效响应频带即可，这样就不必外加激励），通过数据采集系统获得系统的响应信号，再通过模态参数时域识别法（所⽤设备简单，可只根据⾃由响应⽽⽆需激励就可以进⾏参数识别）识别出系统模态，因此具有在⽆需外加激励输⼊和未知激励信号的情况下，识别出数控装备机械结构模态参数的能⼒。

1.2定义模态分析是⼀项对描述系统动⼒学特性所⽤参数进⾏研究和估计的技术，对所有线性动⼒学系统，只要其输⼊输出可以测量，均可通过模态分析进⾏研究1.3基本假设模态分析系统理论的基本假设是：1、线性假设结构的动态特性是线性的，就是说任何输⼊组合引起的输出等于各⾃输出地组合，其动⼒学特性可以⽤⼀组线性⼆阶微分⽅程来描述2、时不变假设结构的动态特性不随时间⽽变化，因⽽微分⽅程的系数是与时间⽆关的常数3、可观测性假设系统动态特性的全部数据都是可以测量的Maxwell互易性原理在q点输⼊所引起的p点的响应等于在p点输⼊引起的q点响应1.4模态参数模态向量——由振动理论知：⼀个线性振动系统，当它按照⾃⾝某⼀阶固有频率作⾃由谐振时，整个系统将具有确定的振动形态简称振型或模态，描述这种振动形态的向量称为振型向量或模态向量。

1.5途径⽤模态分析研究结构的动⼒学特性有两种途径：解析式模态分析结构的⼏何形状、边界条件、材料特性，把结构的质量分布、刚度分布、阻尼分布分别⽤质量矩阵、刚度矩阵和阻尼矩阵表⽰出来，从⽽确定系统的模态参数（固有频率，阻尼系数、模态振型），这些模态参数可以完整的描述系统的动⼒学参数实验模态分析从测量结构（样机）上的某些点的动态输⼊⼒和输出响应，将测量得到的数据转换成频响函数，从测得的频响函数来估计这些模态参数1.6步骤实验模态分析的五步骤：1、建⽴试验“装置”，即固定试件、安装传感器、连接数据采集系统、校准测量系统等2、进⾏数据采集并常常要估计频响函数3、系统识别，即根据测量出来的输⼊输出数据（频响函数）确定系统的动态特性4、对所获得的识别结果进⾏验证5、应⽤系统的⽽不是零散⽅法，根据的道德数据对系统加以改进。

振动与模态分析的主要概念！一、振动的基本问题•已知激励（动载荷）和结构参数，求解结构的振动响应（由输入和系统的参数，求输出）这称为振动正问题。

基于结构动力学分析理论，求结构动力学响应。

•已知激励和振动响应，求结构参数。

这个问题称为振动问题的第一类反问题或系统辨识（系统识别）问题。

•已知结构参数和振动响应，求激励。

这个问题称为振动问题的第二类反问题——（动态）载荷识别问题。

二、描述振动系统的模型•物理参数模型：质量、刚度、阻尼为特征参数的模型。

•模态参数模型：一类以模态频率、模态振型、衰减系数为特征参数，一类以模态质量、模态刚度、模态阻尼、模态矢量（留数）为特征参数。

•非参数模型：频率响应函数（传递函数）、脉冲响应函数都可以反映了振动结构的特性，称为非参数模型。

上述三种模型是等价的。

从系统的物理参数模型（质量、刚度、阻尼）可以得到模态参数模型（模态、频率、衰减系数或模态质量、模态刚度、模态阻尼、模态矢量），进而得到非参数模型（频响函数或脉冲响应函数）。

以上是振动理论的基本内容，也是系统识别的理论基础。

三、振动结构的系统识别•物理参数识别：结构的物理模型为基础，物理参数为识别目标。

是进行结构动力学修改的基础。

•模态参数识别：以模态参数模型为基础，模态参数作为识别目标。

优点：模态参数从整体上反映结构的固有振动特性，需识别的参数少，模态参数识别是系统识别的基本要求，是物理参数识别的基础，也是模态分析的主要任务。

•非参数识别：根据结构的振动所受激励和响应，确定结构的频响函数（或传递函数），或者系统的脉冲响应函数（频响函数与脉冲响应函数构成傅里叶变换对）。

四、模态分析概念•狭义定义：以结构振动理论为基础，以模态参数识别为目标的分析方法，称为模态分析。

•广义定义：模态分析是研究结构物理参数模型、模态参数模型和非参数模型的关系，并通过一定手段确定这些系统模型的理论及其应用的一门学科。

五、模态分析过程根据具体的方法和手段，模态分析分为理论模态分析和实验模态分析。

模态分析的应用模态分析作为一门新的学科得到迅速发展，关键在于其实用性，在于它解决实际工程中振动问题的能力。

模态分析所寻求的最终目标在于改变机械结构系统由经验、类比和静态设计方法微动态、优化设计方法；在于借助于试验与理论分析相结合的方法，对已有结构系统进行识别、分析和评价，从中找出结构系统在动态性能上存在的问题，确保工程结构能安全可靠及有效的工作；在于根据现场测试的数据来诊断及预报诊断故障和进行噪声控制。

通过这些方法为老产品的改进和新产品的设计提供可靠的指导。

模态分析技术的应用可归结为一下几个方面：1. 评价现有结构系统的动态特性；2. 在新产品设计中进行结构动态特性的预估和优化设计；3. 诊断及预报结构系统的故障；4. 控制结构的辐射噪声；5. 识别结构系统的载荷。

自由模态、安装模态、运行模态的区别模态的结构受到三个主要因素的影响:结构在空间的分布情况,也即结构本身,约束,还有就是实际运动情况.约束不同,那么不同的安装带来了不同的模态结果,也即分出了自由/安装模态;约束相同，运动不同，那么不同的运动，也即引入了工作变形（ODS）等.出来的；在约束作用下，有些模态将不能反映出来或者被改变了（引入了新的模态转换坐标），因此，自由模态通过转换/缩减后可以获得约束模态，同时也说明约束对模态起重要作用，如增加约束将提高模态频率，事实上也就是改变了约束程度，增加了联结刚度.安装模态能反映出实际的情况，因为约束和实际是一致的，但安装模态说明的是在安装约束情况下，所有可能的模态情况，并没有考虑实际结构运动，也就是结构真正的工作状态.ODS通常是指结构在某种约束/某种运动条件下表现出来的模态，它是在约束和运动同时作用后考虑的.通过约束模态分析和ODS分析可以判断出约束模态中的几阶对实际运动工作环境下变形的影响•换言之,ODS表现出了真正的运动变形情况，但它是由约束模态的哪几阶组合，需要通过约束模态加以判断，从而获得各阶贡献量，并加以判断，改进.既然引入了运动，那么运动条件也就对ODS产生影响，如转动情况，不同的转速对ODS可能发生影响.此时对应的约束模态也可能改变.模态分析和有限元分析怎么结合使用，用试验模态分析的结果怎么修正有限元分析的结果？模态分析和有限元分析怎么结合使用1。

模态分析原理模态分析是一种用于研究材料结构和性能的重要方法。

通过模态分析，我们可以了解材料在外部力作用下的响应情况，进而指导材料的设计和制备。

本文将介绍模态分析的原理及其在材料科学中的应用。

首先，我们来了解一下模态分析的基本原理。

模态分析是通过对材料的振动特性进行研究来分析其结构和性能。

在模态分析中，我们通常会使用有限元方法来建立材料的数学模型，然后通过数值计算的方式来求解材料的振动模态。

在振动模态分析中，我们可以得到材料在不同频率下的振动模式和振动形态，从而了解材料的结构特性和动态响应。

模态分析在材料科学中有着广泛的应用。

首先，模态分析可以帮助我们了解材料的固有振动特性，包括自然频率、振动模式等。

这对于材料的设计和优化至关重要，可以帮助我们预测材料在不同工况下的响应情况，指导材料的合理设计。

其次，模态分析还可以用于研究材料的损伤和疲劳行为。

通过监测材料在振动过程中的变化，我们可以及时发现材料的损伤情况，预测材料的寿命，从而延长材料的使用寿命。

除此之外，模态分析还可以应用于材料的质量控制和故障诊断。

通过对材料进行振动特性的监测和分析，我们可以及时发现材料的质量问题和故障情况，从而采取相应的措施进行修复和改进。

这对于提高材料的质量和可靠性具有重要意义。

总的来说，模态分析是一种重要的研究方法，可以帮助我们深入了解材料的结构和性能。

通过模态分析，我们可以预测材料在不同工况下的响应情况，指导材料的设计和制备，提高材料的质量和可靠性。

因此，模态分析在材料科学领域具有重要的应用前景，也是当前材料研究的热点之一。

综上所述，模态分析原理是一种重要的研究方法，通过对材料的振动特性进行分析，可以帮助我们了解材料的结构和性能。

模态分析在材料科学中有着广泛的应用，可以指导材料的设计和制备，提高材料的质量和可靠性。

相信随着科学技术的不断发展，模态分析在材料研究领域将会发挥越来越重要的作用。

模态分析（modal）1.概述（Modal and Modal (SAMCEF)）模态分析可以得到结构或者是机器组件的振动特性，包括固有频率和相应的振型。

模态分析定义.doc模态分析可以为其他的分析类型的服务，比如对于一个接触分析，它可以检测结构在无约束的情况下的振动特性（自由模态分析），从而作为接触分析的参照。

除此之外，模态分析作为后续动力学分析的基础，比如谐响应分析，谱分析，随机振动分析。

模态分析得到的结果（固有频率和振型）是在动载荷的作用下，结构设计的重要参数。

You will configure your modal analysis in the Mechanical application, which useseither the ANSYS or the SAMCEF solver, depending on which system you selected,to compute the solution.你将在Mechanical application中完成模态分析过程，你可以选择ANSYS 或者SAMCEF的求解器计算你的分析结果，取决于你所选择的系统。

You can also perform a modal analysis on a prestressed structure, such as aspinning turbine blade.Prestressed modal analysis requires performing a staticstructural analysis first.你也可以在存在预应力的情况下进行模态分析，比如说旋转的涡轮叶片。

但是，在这之前，需要对结构进行静力学分析。

If there is damping in the structure or machine component, the system becomes adamped modal analysis. For a damped modal system, the natural frequencies andmode shapes become complex.如果结构或者机器组件中存在阻尼，系统就变成阻尼模态分析，对于阻尼模态分析，固有频率和振型变得更加复杂。

模态分析基本原理
模态分析是一种用于研究系统的行为和性能的方法。

它可以帮助我们理解系统在不同条件下的行为和响应。

模态分析的基本原理是通过建立数学模型来描述系统的动力学特性。

这个模型通常由一组微分方程组成，描述了系统各个部分之间的相互作用和能量传递。

通过分析这些微分方程的解，可以得到系统的稳态和暂态响应。

为了进行模态分析，首先需要确定系统的状态空间。

状态空间是描述系统状态的一组变量，这些变量可以是位置、速度、加速度等。

状态空间的选择取决于具体问题的需求。

在模态分析过程中，还需要确定系统的边界条件和初始条件。

边界条件描述了系统与外界之间的交互，而初始条件描述了系统在初始时刻的状态。

模态分析通过研究系统的特征方程和特征根来揭示系统的行为模式。

特征方程是通过将系统的微分方程转化为代数方程得到的，而特征根是特征方程的解。

特征根的实部和虚部可以提供关于系统的稳定性和振荡特性的信息。

通过分析特征根，可以确定系统的模态响应。

模态响应描述了系统在不同特征根下的行为，包括稳定性、发散性和振荡性等。

模态分析可以应用于很多领域，包括机械工程、电气工程、控制系统等。

它可以帮助工程师设计和优化系统，提高系统的性
能和可靠性。

总之，模态分析是一种基于数学模型的方法，通过研究系统的行为特性和相互关系来理解和优化系统的性能。

各种模态分析方法总结及比较(共15页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--各种模态分析方法总结与比较一、模态分析模态分析是计算或试验分析固有频率、阻尼比和模态振型这些模态参数的过程。

模态分析的理论经典定义：将线性定常系统振动微分方程组中的物理坐标变换为模态坐标，使方程组解耦，成为一组以模态坐标及模态参数描述的独立方程，以便求出系统的模态参数。

坐标变换的变换矩阵为模态矩阵，其每列为模态振型。

模态分析是研究结构动力特性一种近代方法，是系统辨别方法在工程振动领域中的应用。

模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。

这些模态参数可以由计算或试验分析取得，这样一个计算或试验分析过程称为模态分析。

这个分析过程如果是由有限元计算的方法取得的，则称为计算模记分析；如果通过试验将采集的系统输入与输出信号经过参数识别获得模态参数，称为试验模态分析。

通常，模态分析都是指试验模态分析。

振动模态是弹性结构的固有的、整体的特性。

如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性，就可能预言结构在此频段内在外部或内部各种振源作用下实际振动响应。

因此，模态分析是结构动态设计及设备的故障诊断的重要方法。

模态分析最终目标是在识别出系统的模态参数，为结构系统的振动特性分析、振动故障诊断和预报以及结构动力特性的优化设计提供依据。

二、各模态分析方法的总结（一）单自由度法一般来说，一个系统的动态响应是它的若干阶模态振型的叠加。

但是如果假定在给定的频带内只有一个模态是重要的，那么该模态的参数可以单独确定。

以这个假定为根据的模态参数识别方法叫做单自由度(SDOF)法n1。

在给定的频带范围内，结构的动态特性的时域表达表示近似为：()[]}{}{T R R t r Q e t h rψψλ= 2-1而频域表示则近似为：()[]}}{{()[]2ωλωψψωLR UR j Q j h r tr r r -+-= 2-2 单自由度系统是一种很快速的方法，几乎不需要什么计算时间和计算机内存。

弹性力弹性物体因外力产生形变后的恢复力。

简称弹力。

形变也存在于物体内部，因此物体内部的各部分间都有弹性力相作用。

弹性力有各种名称：相互压缩时，称压力，垂直于物体表面的压力称法向压力；相互拉长时，称张力。

物体给平面或斜面的法向压力的反作用力，称支持力或反力，实质上也是压力。

一定范围内弹性力和变形程度成正比，这个范围称弹性限度。

在限度内，撤去外力，物体能恢复原状；超过这限度，变形程度不再和外力成正比，撤去外力后物体也不能恢复原状。

对弹簧来说，弹性力为F=－kx，x表示弹簧终端的位移，k 为弹性力和位移值之比，称刚度系数，负号表示弹性力的方向与位移的方向相反。

弹性力也是保守力，弹性力作功可用弹性势能表示，其值为，x为位移的值。

在外力作用下弹性物体形变后所产生的一种恢复力。

弹性力的特点是它在变形体上所做的功并不转化为热，但可转化为势能。

弹性力是一种保守力。

物体中任何两个质点相对位置的变化，称为物体变形。

当物体的形变很小时，弹性力F和物体中质点M开平衡位置时的位移成正比,其方向指向力图使质点复到平衡位置的方向。

固有振动固有振动是指物质系统在不受到与时间有关的外界作用而阻尼又可忽略的情况下所发生的振动。

又称自由振动、自然振动、本征振动（是天文学专有名词）。

固有振动的振幅决定于振动起始时系统所具有的能量。

固有振动的频率称为固有频率，只与振动系统的固有条件有关（如弹性和惯性，电容和电感等，见振动）。

物理系统（包括机械、电磁或其它类型的振动）从外界取得一定的能量开始振动以后，不再受外界作用而阻力又可忽略的情况下，仅在内部弹性力或准弹性力作用下，以固有频率而保持振幅恒定的振动状态叫“固有振动”。

固有振动的振幅决定于系统开始振动时所具有的能量，但频率则完全取决于系统本身的性质。

例如被击动后鼓膜的振动，弹簧振子偏离平衡位置后无外力作用下的振动等都是“自由振动”。

自由振动在外力使弹簧振子的小球和单摆的摆球偏离平衡位置后，它们就在系统内部的弹力或重力作用下振动起来，不再需要外力的推动，这种振动叫做自由振动。