高精度差分格式及可压缩湍流数值模拟(一)

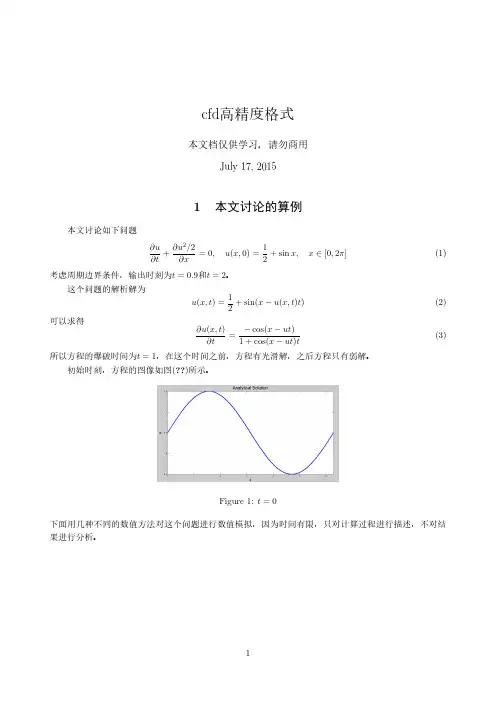
一维不可压缩navier stokes方程理论说明1. 引言1.1 概述本文将讨论一维不可压缩Navier-Stokes方程的理论说明。

Navier-Stokes方程是描述流体运动的基本方程之一，其在各个领域都具有重要应用价值。

本文将从介绍Navier-Stokes方程的基本概念开始，逐步展开对一维流动特征和不可压缩流体模型假设的理论说明。

1.2 文章结构文章分为五个主要部分：引言、一维不可压缩Navier-Stokes方程理论说明、理论推导和分析、数值方法和模拟研究以及结论与展望。

其中，引言部分将概述文章的目标和结构，提供读者对整篇文章内容的预览。

1.3 目的本文旨在深入探讨一维不可压缩Navier-Stokes方程，并通过理论推导和数值模拟研究解析该方程对流体运动行为的描述能力。

通过阐明不同数值方法在求解此类方程时的差异和优劣，我们可以更好地了解该方程在实践中的应用，并为进一步研究提供展望。

以上是关于引言部分的详细内容，请根据需要进行修改或补充。

2. 一维不可压缩Navier Stokes方程理论说明2.1 Navier Stokes方程简介Navier Stokes方程是描述流体运动的基本方程之一，它由质量守恒和动量守恒两个方程组成。

同时考虑流体的黏性和压力力作用，Navier Stokes方程能够准确描述流体在各种复杂情况下的运动。

2.2 一维流动特征描述在一维流动中，流体只在一个空间方向上（通常为x轴）有速度分量变化，而在其余两个空间方向上（通常为y轴和z轴）没有速度分量变化。

这样简化后的一维问题可以更容易地推导出Navier Stokes方程的解析解，并且提供了更直观的物理图像。

2.3 不可压缩流体模型假设不可压缩流体是指在任何情况下密度保持不变，即密度是常数。

这个假设适用于许多情况下，例如液体的非常小压缩性以及稳态条件下气体的高马赫数等。

通过这个假设，我们可以将Navier Stokes方程进一步简化为不含密度项的形式，并且使问题更具可行性。

对流方程的四阶中心差分格式流体动力学中，流体动力学方程是用来描述流体在非平衡状态下的运动特性的常微分方程。

它描述的是物质的密度和流动速度的变化，作为时间变化的外力的影响。

流体动力学方程的四阶中心差分格式是一种在数值模拟中应用广泛的解析方法。

一、四阶中心差分格式的简介四阶中心差分格式是一种应用于数值模拟的新方法，它利用中心差分法将流体动力学方程式划分为一系列离散的微分方程，从而能够更准确地描述流体动力学过程。

有一组离散的普通微分方程以及一组离散的非线性方程构成了四阶中心差分格式的核心。

四阶中心差分格式与传统的中心差分格式相比，能够更快更准确地收敛，因此是一种实际应用中的优良方法。

二、优势1、四阶中心差分格式具有较好的精度、可靠性和通用性。

与传统的中心差分格式相比，该方法更加准确地收敛，以及更快地收敛。

2、操作简单，实施方便。

和传统的中心差分格式相比，四阶中心差分格式不仅具有准确性，而且操作简单，实施方便。

3、运算量较小，性能稳定。

对于四阶中心差分格式，其运算量比传统的中心差分格式要小，且性能稳定，更容易用于模拟流体动力学过程。

三、应用1、应用于流体动力学模拟。

四阶中心差分格式可以应用于地形线、边界条件、热流和微外质，从而模拟流体动力学过程。

2、用于求解复杂的流体动力学问题。

该格式由微分方程和非线性方程构成，可以用于求解复杂的流体动力学问题，如湍流流动、不规则流动等。

3、用于水力参数的表达。

此外，四阶中心差分格式也可以用来表达不同的水力参数，如流速、湍流度、温度分布等。

四、缺陷1、四阶中心差分格式伴随着较大的计算量，可能会导致计算速度下降。

2、四阶中心差分格式实施起来可能会比较复杂，可能会消耗更多的精力和时间。

3、四阶中心差分格式可能会受到流体边界条件等外部影响，从而产生模拟误差。

大型客机复杂可压缩流的大涡模拟主要研究方法一、大涡模拟基础1. 大涡模拟简介大涡模拟是一种将流场分解成小尺度湍流和大尺度湍流的方法。

在LES中，大尺度结构通过直接数值模拟来求解，而小尺度结构则通过子网格模型（sub-grid model）进行建模。

由于小尺度结构不再需要直接求解，因此可以使用更粗的网格来进行计算，从而减少计算量。

同时，LES还能够提供更加真实的湍流统计数据，如湍流强度、湍流长度等。

2. LES的优点和局限性与其他流体力学方法相比，LES有以下几个优点：（1）能够考虑湍流中的时间和空间尺度差异，提供更加真实的湍流信息；（2）计算结果对于网格的依赖性相对较小，使得计算可以在较粗的网格上进行；（3）LES能够模拟复杂流场，如湍流燃烧、多相流等。

虽然LES具有很多优点，但它也有一些局限性：（1）计算量较大，需要使用高性能计算机进行计算；（2）由于需要建立子网格模型，LES的结果可能受到模型误差的影响；（3）由于直接数值模拟只考虑了大尺度结构，因此对于小尺度结构的预测可能存在误差。

二、大涡模拟在大型客机流场研究中的应用1. 大涡模拟在飞行器气动力学研究中的应用大型客机的外形复杂，流场也非常复杂。

对于这样的流场，传统的计算流体力学方法可能无法准确地预测气动力学行为。

因此，大涡模拟成为研究大型客机流场的一种重要方法。

在大涡模拟中，通过将流场分解成大尺度结构和小尺度结构，可以更加准确地模拟大型客机流场中的湍流现象。

大涡模拟还能够提供更加真实的气动力学数据，如升阻比、气动力矩等。

这些数据对于飞机设计和优化非常重要。

2. 大涡模拟在飞行器噪声研究中的应用随着人们对噪声污染的关注度不断提高，飞机噪声研究也越来越受到关注。

大型客机飞行时产生的噪声主要来自于引擎和机翼表面的湍流。

由于湍流现象非常复杂，传统的计算流体力学方法无法准确地预测噪声的产生和传播。

因此，大涡模拟成为研究飞机噪声的一种重要方法。

通过大涡模拟，可以更加准确地模拟湍流现象，从而预测噪声的产生和传播方式。

有限体积WENO格式及其应用在数值模拟领域，有限体积WENO（Weighted EssentiallyNon-Oscillatory）格式是一种广泛使用的非线性数值逼近方法，适用于解决流体力学中的各种问题。

由于其具有高精度、低振荡和低数值弥散等优点，有限体积WENO格式在气象预报、气候模拟、流体动力学等领域中得到了广泛应用。

本文将详细介绍有限体积WENO格式的定义、特点、应用、优势、不足以及结论。

有限体积WENO格式是一种基于有限体积方法的气象预报和流体动力学数值模拟算法。

该方法通过非线性加权差分函数，在每个控制体网格中心进行积分，进而得到流体的宏观量如速度、压力等在该网格中心的数值近似。

高精度：有限体积WENO格式具有高精度的特点，能够准确捕捉到流体的详细变化特征。

低振荡：由于有限体积WENO格式采用非线性加权差分函数，因此能够有效避免数值振荡现象，提高模拟结果的稳定性。

低数值弥散：有限体积WENO格式在模拟过程中产生的数值弥散较小，能够更好地保持流场的结构特征。

有限体积WENO格式在气象预报、气候模拟、流体动力学等领域中得到了广泛应用。

例如，在气象预报领域，有限体积WENO格式被广泛应用于天气预报和气候预测。

在流体动力学领域，有限体积WENO格式被用于模拟湍流、燃烧等复杂流动现象。

在这些应用中，有限体积WENO格式都展现出了其高精度、低振荡和低数值弥散等优点。

有限体积WENO格式在实际应用中具有以下优势：高精度：有限体积WENO格式能够准确捕捉到流体的变化特征，提高模拟结果的精度。

适用范围广：有限体积WENO格式适用于各种复杂流动现象的模拟，能够适应不同领域的需求。

稳定性好：由于有限体积WENO格式采用非线性加权差分函数，能够有效避免数值振荡现象，提高模拟结果的稳定性。

计算效率高：有限体积WENO格式的计算效率较高，适用于大规模并行计算，能够处理大规模问题。

虽然有限体积WENO格式具有许多优点，但也存在一些不足之处：计算成本较高：由于有限体积WENO格式需要进行非线性加权差分函数的计算，因此需要消耗更多的计算资源，导致计算成本较高。

§6. 通量差分 6.1 Godunov 格式简介Godunov 格式是可压缩流动数值算法发展过程中的一个重要成果，对通量差分等方法的产生和发展起到了直接的促进作用。

这一方法还是非线性问题（一维气体力学方程组）数值方法中第一个被证明能够收敛到方程弱解的格式，在这之前都是用线化模型方程研究格式的收敛性。

但由于这种方法的计算量现在看起来都很大，以当时计算机的发展水平更是难以承受，所以其实用性较差。

考虑守恒律方程组()t x¶¶+=抖f w w 0 Godunov 方法的求解过程中有两个关键步骤：• 精确求解Riemann 问题：在Godunov 格式中，每一个网格上的计算是通过求Riemann 问题的解析解来完成的，得到的是在整个网格内处处有定义的函数解（间断除外）。

而通常的差分格式得到的是仅在网格点上有定义的离散解。

• 平均：由于Godunov 格式给出的是函数解，为了让计算能够进行下去，需要计算解函数在网格上的平均值。

这一做法后来发展成各种高阶重构方法，到现在还在使用。

上图给出了Godunov 方法的示意图，计算的步骤简述如下。

设在 n t t = 时刻，已经得到数值解函数 (),n x t w% 。

在以 j x 为中心的网格 1122,j j x x -+轾犏臌上，将 (),n x t w % 看成常数 n jw 。

当然，最简单的做法就是取 (),n x t w % 在网格点上的值 (),n nj jx t =w w % 。

但是，取 (),n x t w% 在网格上的平均值()12121,j j xn n jxt d x+-=D òw w%ξξ 精度更高一些。

事实上，由泰勒展开()()()()2221,,2nn jj j j jt x t x x x x 抖=+?+?+¶¶wwww%%%%L ξξξ代入上述积分，有()()()()()1212112211222222211,21,1 2j j j j j j xn n jjj j xj jx x nj j x xj j x t x x d x x x x t d x d xx x +-++--轾抖犏=+?+?+犏D ?¶犏臌ì骣ï¶÷ïç÷ç=??í÷ç÷ïçD ?÷桫ïïî骣÷¶ç÷ç+?÷ç÷ç¶÷ç桫ò蝌w ww w w w w %%%L %%%ξξξξξξ()12122j j x j x x d +-üïïï-+ýïïïþòL ξξ令 j y x =-ξ ，继续计算，()()11122211122222223211,2111,2120x xxnn j j x xx j j n j j j x t dy ydyy dy xx x x t x x x x x D D D -D -D -D 禳骣骣镲÷抖秣?çç镲÷÷çç=???÷睚÷çç÷÷ç镲çD ?÷¶÷ç桫镲桫镲铪ì骣骣ï÷抖秣ççï÷÷çç=譊+?譊+÷í÷çç÷÷ççD ?÷¶÷ç桫桫蝌?w w w w w w w %%%L%%%L ()()2,n j x t x üïïïý镲镲镲铪=+D w%O由此可见，作为函数 (),n x t w % 在网格上的常数近似，网格平均比网格点处的值 (),n j x t w% 精度更高。

4月1日写给Fluent新手(续)31 数值模拟过程中,什么情况下出现伪扩散的情况？以及对于伪扩散在数值模拟过程中如何避免？假扩散（false diffusion）的含义：基本含义：由于对流—扩散方程中一阶导数项的离散格式的截断误差小于二阶而引起较大数值计算误差的现象。

有的文献中将人工粘性（artificial viscosity）或数值粘性（numerical viscosity）视为它的同义词.拓宽含义：现在通常把以下三种原因引起的数值计算误差都归在假扩散的名称下1.非稳态项或对流项采用一阶截差的格式;2。

流动方向与网格线呈倾斜交叉(多维问题）;3。

建立差分格式时没有考虑到非常数的源项的影响。

克服或减轻假扩散的格式或方法，为克服或减轻数值计算中的假扩散(包括流向扩散及交叉扩散)误差,应当：1. 采用截差阶数较高的格式；2。

减轻流线与网格线之间的倾斜交叉现象或在构造格式时考虑到来流方向的影响。

3. 至于非常数源项的问题，目前文献中，还没有为克服这种影响而专门构造的格式，但是高阶格式显然对减轻其影响是有利的。

32 FLUENT轮廓（contour)显示过程中，有时候标准轮廓线显示通常不能精确地显示其细节，特别是对于封闭的3D物体(如柱体)，其原因是什么？如何解决?FLUENT等高线(contour）显示过程中，可以通过调节显示的水平等级来调节其显示细节,Levels..。

最大值允许设置为100.对于封闭的3D物体，可以通过建立Surface，监视Surface 上的量来显示计算结果.或者计算之后将结果导入到Tecplot中，作切片图显示。

33 如果采用非稳态计算完毕后,如何才能更形象地显示出动态的效果图？对于非定常计算，可以通过创建动画来形象地显示出动态的效果图。

Solve—>Animate->Define。

.。

，具体操作请参考Fluent用户手册。

34 在FLUENT的学习过程中,通常会涉及几个压力的概念，比如压力是相对值还是绝对值？参考压力有何作用？如何设置和利用它？GAUGE PRESSURE 就是静压。

渐缩渐扩管的流动是计算流体力学模拟的经典问题之一。

在这类流动中，激波的出现是流动中可压缩效应的体现。

精确的激波模拟是CFD 研究的热点之一。

为了更好捕捉压力梯度，需要采用较细的网格并结合合适的数值模拟和格式。

很多实际模拟中，局部网格的自适应会很有帮助。

一、Double Precision 的选择如果几何模型包含多个通过小直径管道相互连接的体，而某一个区域的压力特别大（因为用户只能设定一个总体的参考压力位置），此时，双精度求解器可能更能体现压差带来的流动（如渐缩渐扩管的无粘与可压缩流动模拟）。

二、操作条件对于可压缩流动的计算，推荐在Define/Operating Conditions 中将工作压力设为0，从而，最小化由于压力脉动而引起的误差。

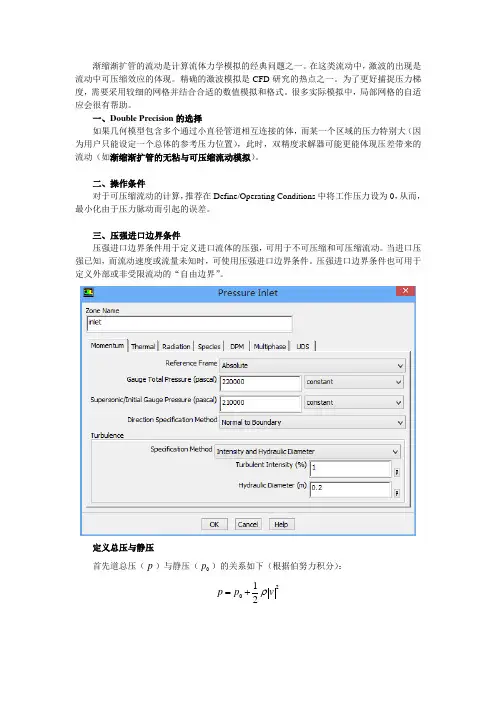
三、压强进口边界条件压强进口边界条件用于定义进口流体的压强，可用于不可压缩和可压缩流动。

当进口压强已知，而流动速度或流量未知时，可使用压强进口边界条件。

压强进口边界条件也可用于定义外部或非受限流动的“自由边界”。

定义总压与静压首先道总压（p ）与静压（0p ）的关系如下（根据伯努力积分）：2012p p v ρ=+在Momentum （动量）选项卡内，Reference Frame 为参考值，有绝对值（Absolute ）与相对于临近区域值（Relative to Adjacent Zone ）两个选项供选择，一般保持默认的绝对值，Gauge Total Pressure （表总压）文本框中输入总压的值。

静压在FLUENT 中被称为Supersonic/Initial Gauge Pressure （超音速/初始表压），如果进口流动是超音速的或者是准备压强进口边界条件进行计算的初始化工作，则必须定义静压。

在流场为亚音速时，FLUENT 将忽略Supersonic/Initial Gauge Pressure （超音速/初始表压）的输入数据，而用驻点参数求出静压。

基于高精度weno差分格式的amr方法基于高精度weno差分格式的AMR方法（Adaptive Mesh Refinement, AMR）是一种处理复杂物理问题的可扩展解决方案。

它将复杂的多项式网格系统用作数值模拟的基础，并通过在模拟结果中发现高度复杂的区域来实现更高精度的数值模拟。

它依赖于WENO差分格式（Weighted Essentially Non-oscillatory Scheme, WENO）来实施AMR，从而可以根据动态准则生成更小的网格并将其用于更精细的模拟。

WENO差分格式是一种新型的数值求解方法，主要用于解决非线性偏微分方程组。

WENO使用数值技术重新定义了有限差分格式，使其能够实现更高精度的计算，同时保持非振荡特性。

WENO是一种非常有效的快速计算方法，由于它的非振荡性和高精度，它被广泛应用于各种科学计算中。

基于WENO差分格式的AMR方法可以在模拟的过程中逐步改善网格的分辨率，从而实现更高精度的模拟。

AMR的核心在于周期性地检测模拟结果中存在的复杂状态，然后对其进行更细致的数值模拟。

WENO差分格式用于AMR时，可以将大小相关的局部变化分解为小尺寸的片段，这样就可以使用非振荡方法来获得高精度的结果。

在网格系统中，WENO差分格式可以在模拟过程中持续性地改善网格的分辨率，从而实现更高精度的模拟效果。

基于WENO差分格式的AMR方法的优点是它对复杂的物理问题具有较强的适应性，并具有高度的内存使用效率和计算效率。

它可以自动识别模拟结果中的复杂状态，然后将其分隔为小片段用于更细致的模拟。

另外，WENO差分格式用于AMR时，它可以进行更精细的计算，提高计算效率和模拟的精度。

在模拟的过程中，AMR可以根据模拟结果的复杂性自动更新网格，从而减少模拟时间。

总的来说，基于高精度weno差分格式的AMR方法具有非常强的适应性，可提高模拟效率和精度，平衡存储和计算开销，为复杂物理问题提供完整的解决方案。