下载文档原格式
%拉格朗日插值方法%可以同时对多点插值%t可以为向量function s=lag(x,y,t)%采用符号推导，这样可以给出插值具体公式syms p;%读取x向量维数n=length(x);s=0;for(k=1:n)la=y(k);%构造基函数for(j=1:k-1)la=la*(p-x(j))/(x(k)-x(j));end;for(j=k+1:n)la=la*(p-x(j))/(x(k)-x(j));end;s=s+la;simplify(s);end%对输入参数个数做判断，如果只有两个参数%直接给出插值多项式%如果三个参数则给出插值点的插值结果%第三个参数可以为向量if(nargin==2)s=subs(s,'p','x');%展开多项式s=collect(s);%把系数取到6位精度表达s=vpa(s,4);else%读取t长度m=length(t);%分别对t的每一个分量插值for i=1:mtemp(i)=subs(s,'p',t(i));end%得到的是系列插值点的插值结果%既得到的是向量，赋值给ss=temp;end%lagrange方法主函数%同时计算多点插值%已有点x ，yx=[pi/4,pi/6,pi/3,pi/2];y=[cos(pi/4),cos(pi/6),cos(pi/3),cos(pi/2)];%需要插值点t=[-40*pi/180,47*pi/180,53*pi/180,79*pi/180,174*pi/180]; disp('角度')du=[-40 47 53 79 174]%插值计算结果disp('插值结果')yt=lag(x,y,t)%cos函数值disp('cos函数值')yreal=[cos(-40*pi/180)cos(47*pi/180)cos(53*pi/180)cos(79*pi/180)cos(174*pi/180)]'disp('插值与函数值误差')dy=yt-yreal%给出插值多项式，需要显示的话去掉下行的分号yt=lag(x,y)%画出插值多项式图形ezplot(yt,[-pi/4,pi])hold on%画出cos函数图形ezplot('cos(t)',[-pi/4,pi]);grid onhold off。
第六章 插值与逼近一、Lagrange 插值问题定义：设函数f(x)在区间[a,b]有定义，在[a,b]上的n+1个不同的点x 0、x 1……x n 处的函数值y i =f(x i )已知，求一个至多n 次多项式P n (x)=a 0+a 1x+a 2x2+a 3x 3+a n x n使满足P n (x i )=f(x i ) （i=0,1……n ），则称P n (x)为插值多项式，式子中x 0、x 1……x n 称为插值节点，[a,b]称为插值区间。
P n (x)中有n+1个特定系数a n ，由P n (x i )=f(x i )得▲ 最简单的情形是只有2个点x 1、x 2，设P n (x)=a 0+a 1x，满足：将a 0和a 1的值带到插值多项中得到：VB 语句表示：p1=y0*(x-x1)/(x0-x1)+y1*(x-x0)/(x1-x0) 总结：2点1次插值也称线性插值。
▲ 讨论三个节点x 1、x 2、x 3的插值多项式：P n (x)=a 0+a 1x+a 2x2，满足：x- x 1X 0- X 1P 1(x)=y 0*+y 1*x- x 0 x 1- x 0a 0+a 1x 0+a 2x 02+a 3x 03+a n x 0n =y 0 a 0+a 1x 1+a 2x 12+a 3x 13+a n x 1n =y 1 ……a 0+a 1x n +a 2x n 2+a 3x n 3+a n x n n =y ny 1x 0- y 0x 1X 0- X 1a 0=从方程中解得：a 1=y 0- y 1 x 0- x 1Lagrange 插值：建立一个简单函数，使这个简单函数经过给定点。
a 0+a 1x 0 =y 0a 0+a 1x 1=y1a 0= x 1x 2 y 0/a+ x 0x 2 y 1/b +x 0x 1 y 2/c a 1= -( x 1+x 2 )y 0/a- (x 0+x 2) y 1/b –(x 0+x 1) y 2/c a 2= y 0/a+ y 1/b + y 2/c 其中a=( x 0- x 1)( x 0- x 2) b=( x 1- x 0)( x 1- x 2) c=( x 2- x 0)( x 2- x 1)3点2次（2阶）插值多项式为：p2=y0*(x-x1)*(x-x2)/((x0-x1)*(x0-x2))+y1*(x-x0)*(x-x2)/((x1-x0)*(x1-x2))+y2*(x-x0)*(x-x1)/((x2-x0)*(x2-x1))总结：二次插值就是用过三点（x 0,y 0）、（x 1,y 1）、（x 2,y 2）的抛物线来近似曲线y=f(x),因此也称三点二次插值为抛物线插值。
常见的插值方法及其原理1. 拉格朗日插值法（Lagrange Interpolation）拉格朗日插值法是一种基于多项式的插值方法，通过n+1个已知点的函数值来构造一个n次多项式。
具体的计算公式如下：L(x) = Σ[yk * lk(x)], k=0 to n其中yk为已知点（xi, yi）的函数值，lk(x)为拉格朗日基函数，定义为：lk(x) = Π[(x - xj)/(xi - xj)], j=0 to n, j≠k拉格朗日插值法的原理是通过构造一个通过已知点的n次多项式，来代替未知函数的近似值。
利用拉格朗日基函数的性质，可以保证插值多项式通过已知点。
2. 牛顿插值法（Newton Interpolation）牛顿插值法是一种递推的插值方法，通过已知点的函数值和差商来逐步构造插值多项式。
差商的定义如下：f[x0]=y0f[x1]=(f[x1]-f[x0])/(x1-x0)f[x2]=(f[x2]-f[x1])/(x2-x1)...f[xn] = (f[xn] - f[xn-1]) / (xn - xn-1)利用差商的定义，可以得到牛顿插值多项式的表达式：N(x) = f[x0] + f[x0, x1](x-x0) + f[x0, x1, x2](x-x0)(x-x1) + ... + f[x0, x1, ..., xn](x-x0)(x-x1)...(x-xn)牛顿插值法的原理是通过递推计算差商来得到插值多项式。
通过使用差商来处理已知点的函数值差异，可以得到更高次的插值多项式。
3. 样条插值法（Spline Interpolation）样条插值法是一种基于分段低次插值函数的插值方法，常用的是三次样条插值。
样条插值法通过寻找一组分段函数，使得满足原函数的插值条件，并要求函数在每个插值点处的函数值、一阶导数和二阶导数连续。
这样可以保证插值函数在每个插值点处的平滑性。
三次样条插值法的原理是将整个插值区间划分为多个小区间，在每个小区间内使用三次多项式进行插值。
拉格朗⽇（Lagrange）插值算法拉格朗⽇插值（Lagrange interpolation）是⼀种多项式插值⽅法，指插值条件中不出现被插函数导数值，过n+1个样点，满⾜如下图的插值条件的多项式。
也叫做拉格朗⽇公式。
这⾥以拉格朗⽇3次插值为例，利⽤C++进⾏实现：1//利⽤lagrange插值公式2 #include<iostream>3using namespace std;45double Lx(int i,double x,double* Arr)6 {7double fenzi=1,fenmu=1;8for (int k=0;k<4;k++)9 {10if (k==i)11continue;12 fenzi*=x-Arr[k];13 fenmu*=Arr[i]-Arr[k];14 }15return fenzi/fenmu;16 }1718int main()19 {20double xArr[4]={};21double yArr[4]={};22//输⼊4个节点坐标23 cout<<"请依次输⼊4个节点的坐标:"<<endl;24for (int i=0;i<4;i++)25 cin>>xArr[i]>>yArr[i];2627//输⼊要求解的节点的横坐标28 cout<<"请输⼊要求解的节点的横坐标:";29double x;30 cin>>x;31double y=0;32for (int i=0;i<4;i++)33 y+=Lx(i,x,xArr)*yArr[i];34 printf("x=%lf时，y=%lf\n",x,y);3536//分界，下⾯为已知y求x37 cout<<"请输⼊要求解的节点的纵坐标:";38 cin>>y;39 x=0;40for (int i=0;i<4;i++)41 x+=Lx(i,y,yArr)*xArr[i];42 printf("y=%lf时，x=%lf\n",y,x);4344 system("pause");45return0;46 }作者：耑新新，发布于转载请注明出处，欢迎邮件交流：zhuanxinxin@。
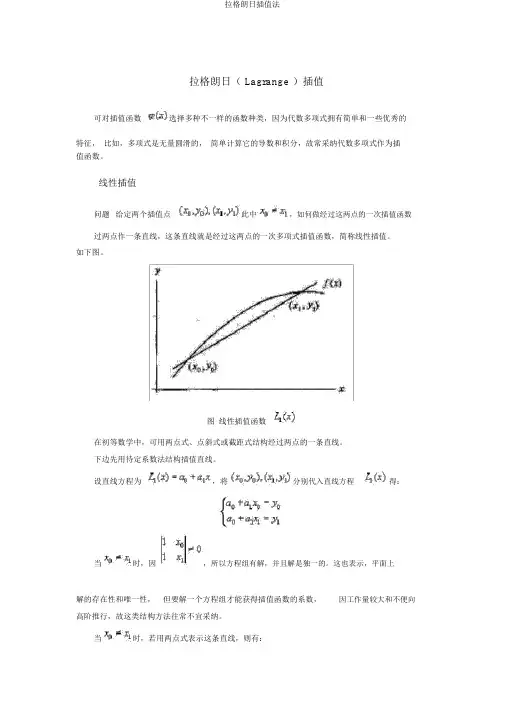
拉格朗日（ Lagrange ）插值可对插值函数选择多种不一样的函数种类，因为代数多项式拥有简单和一些优秀的特征，比如，多项式是无量圆滑的，简单计算它的导数和积分，故常采纳代数多项式作为插值函数。
线性插值问题给定两个插值点此中，如何做经过这两点的一次插值函数过两点作一条直线，这条直线就是经过这两点的一次多项式插值函数，简称线性插值。
如下图。
图线性插值函数在初等数学中，可用两点式、点斜式或截距式结构经过两点的一条直线。
下边先用待定系数法结构插值直线。
设直线方程为，将分别代入直线方程得：当时，因，所以方程组有解，并且解是独一的。
这也表示，平面上解的存在性和唯一性，但要解一个方程组才能获得插值函数的系数，因工作量较大和不便向高阶推行，故这类结构方法往常不宜采纳。
当时，若用两点式表示这条直线，则有：（）这类形式称为拉格朗日插值多项式。
，，称为插值基函数，计算，的值，易见（）在拉格朗日插值多项式中可将看做两条直线，的叠加，并可看到两个插值点的作用和地位都是同等的。
拉格朗日插值多项式型式免去认识方程组的计算，易于向高次插值多项式型式推行。
线性插值偏差定理记为以为插值点的插值函数，。
这里，设一阶连续可导，在上存在，则对随意给定的，起码存在一点，使（）证明令，因是的根，所以可设对任何一个固定的点，引进协助函数：则由定义可得别在和和，即。
，这样起码有上应用洛尔定理，可知和，对3个零点，不失一般性，假设在每个区间起码存在一个零点，不如记为在上应用洛尔定理，获得，分在上起码有一个零点，。
此刻对求二次导数，此中的线性函数)，故有代入，得所以即二次插值问题给定三个插值点，, 此中互不相等，如何结构函数的二次的（抛物线）插值多项式平面上的三个点能确立一条次曲线，如下图。
图三个插值点的二次插值仿制线性插值的拉格朗日插值，即用插值基函数的方法结构插值多项式。
设每个基函数是一个二次函数，对来说，要求是它的零点，所以可设同理，也相对应的形式，得将代入，得同理将代入获得和的值，以及和的表达式。
数值分析实验报告任课教师：马季骕 班级：11级计算机科学与技术1 实验目的及要求2 程序的源代码3 实验操作4 实验结果及分析1 实验目的及要求使用Lagrange 插值的方法求原函数的逼近函数。
在数学分析中，用y=f （x ）来描述一条平面直线，但是在实际问题中，函数y=f （x ）往往是通过观测得到的一组数据来给出的，只是已知个别点的函数值，而非在整个区间上，插值法是应用十分广泛的一种方法。
本实验是用拉格朗日法来逼近被逼近函数，并画出其图像。
当给出了n+1个节点上f (x )的一张函数表后，用Lagrange 插值法求一个函数ϕ(x )，并满足以下两个条件：（1）ϕ(x )是一个不超过n 次的多项式；（2）在给定点)(n 0,1,i x i ⋯=上与)(i x f 取相同值，即)(i x ϕ=)(i x f （i=0,1,2…n ）。
当插值节点取的足够多时逼近函数ϕ(x )能够很好的逼近被逼近函数f (x )。
而插值函数ϕ(x )的次数就会相应地升高，高次的插值多项式就不一定收敛到相应的被逼近函数，就会产生Runge 现象，本实验可以从函数的图像上清楚地看到这一现象。
2 程序的源代码// 数值分析Dlg.cpp : implementation file//#include "stdafx.h"#include "数值分析.h"#include "数值分析Dlg.h"#ifdef _DEBUG#define new DEBUG_NEW#undef THIS_FILEstatic char THIS_FILE[] = __FILE__;#endif///////////////////////////////////////////////////////////////////////////// // CAboutDlg dialog used for App Aboutclass CAboutDlg : public CDialog{public:CAboutDlg();// Dialog Data//{{AFX_DATA(CAboutDlg)enum { IDD = IDD_ABOUTBOX };//}}AFX_DATA// ClassWizard generated virtual function overrides//{{AFX_VIRTUAL(CAboutDlg)protected:virtual void DoDataExchange(CDataExchange* pDX); // DDX/DDV support //}}AFX_VIRTUAL// Implementationprotected://{{AFX_MSG(CAboutDlg)//}}AFX_MSGDECLARE_MESSAGE_MAP()};CAboutDlg::CAboutDlg() : CDialog(CAboutDlg::IDD){//{{AFX_DATA_INIT(CAboutDlg)//}}AFX_DATA_INIT}void CAboutDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CAboutDlg)//}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CAboutDlg, CDialog)//{{AFX_MSG_MAP(CAboutDlg)// No message handlers//}}AFX_MSG_MAPEND_MESSAGE_MAP()///////////////////////////////////////////////////////////////////////////// // CMyDlg dialogCMyDlg::CMyDlg(CWnd* pParent /*=NULL*/): CDialog(CMyDlg::IDD, pParent){//{{AFX_DATA_INIT(CMyDlg)// NOTE: the ClassWizard will add member initialization here //}}AFX_DATA_INIT// Note that LoadIcon does not require a subsequent DestroyIcon in Win32 m_hIcon = AfxGetApp()->LoadIcon(IDR_MAINFRAME);}void CMyDlg::DoDataExchange(CDataExchange* pDX){CDialog::DoDataExchange(pDX);//{{AFX_DATA_MAP(CMyDlg)// NOTE: the ClassWizard will add DDX and DDV calls here //}}AFX_DATA_MAP}BEGIN_MESSAGE_MAP(CMyDlg, CDialog)//{{AFX_MSG_MAP(CMyDlg)ON_WM_SYSCOMMAND()ON_WM_PAINT()ON_WM_QUERYDRAGICON()ON_BN_CLICKED(IDC_NEW, OnNew)ON_BN_CLICKED(IDC_LAG, OnLag)ON_BN_CLICKED(IDC_LINE, OnLine)ON_BN_CLICKED(IDC_HER, OnHer)//}}AFX_MSG_MAPEND_MESSAGE_MAP()///////////////////////////////////////////////////////////////////////////// // CMyDlg message handlersBOOL CMyDlg::OnInitDialog(){CDialog::OnInitDialog();// Add "About..." menu item to system menu.// IDM_ABOUTBOX must be in the system command range.ASSERT((IDM_ABOUTBOX & 0xFFF0) == IDM_ABOUTBOX);ASSERT(IDM_ABOUTBOX < 0xF000);CMenu* pSysMenu = GetSystemMenu(FALSE);if (pSysMenu != NULL){CString strAboutMenu;strAboutMenu.LoadString(IDS_ABOUTBOX);if (!strAboutMenu.IsEmpty()){pSysMenu->AppendMenu(MF_SEPARATOR);pSysMenu->AppendMenu(MF_STRING, IDM_ABOUTBOX, strAboutMenu);}}// Set the icon for this dialog. The framework does this automatically // when the application's main window is not a dialogSetIcon(m_hIcon, TRUE); // Set big iconSetIcon(m_hIcon, FALSE); // Set small icon// TODO: Add extra initialization herereturn TRUE; // return TRUE unless you set the focus to a control}void CMyDlg::OnSysCommand(UINT nID, LPARAM lParam){if ((nID & 0xFFF0) == IDM_ABOUTBOX){CAboutDlg dlgAbout;dlgAbout.DoModal();}else{CDialog::OnSysCommand(nID, lParam);}}// If you add a minimize button to your dialog, you will need the code below// to draw the icon. For MFC applications using the document/view model,// this is automatically done for you by the framework.void CMyDlg::OnPaint(){if (IsIconic()){CPaintDC dc(this); // device context for paintingSendMessage(WM_ICONERASEBKGND, (WPARAM) dc.GetSafeHdc(), 0);// Center icon in client rectangleint cxIcon = GetSystemMetrics(SM_CXICON);int cyIcon = GetSystemMetrics(SM_CYICON);CRect rect;GetClientRect(&rect);int x = (rect.Width() - cxIcon + 1) / 2;int y = (rect.Height() - cyIcon + 1) / 2;// Draw the icondc.DrawIcon(x, y, m_hIcon);}else{CDialog::OnPaint();}}// The system calls this to obtain the cursor to display while the user drags // the minimized window.HCURSOR CMyDlg::OnQueryDragIcon(){return (HCURSOR) m_hIcon;}void CMyDlg::OnNew(){// TODO: Add your control notification handler code hereint x00=225,y00=225,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);//画坐标轴与原函数for(i=-650; i<=650; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}for(x=-1; x<=1; x+=0.001){double j=400.0/(1+25*x*x);pDC->SetPixel(x*500,j,RGB(255,0,0));}}void CMyDlg::OnLag(){// TODO: Add your control notification handler code here int x00=225,y00=225,i,j;double x;CDC *pDC=GetDC();pDC->SetMapMode(MM_LOMETRIC);pDC->SetViewportOrg(x00,y00);//画坐标轴for(i=-650; i<=650; i++){pDC->SetPixel(i,0,RGB(0,0,0));pDC->SetPixel(0,i,RGB(0,0,0));}double yx[]={-1,-0.8,-0.6,-0.4,-0.2,0,0.2,0.4,0.6,0.8,1};// 拉格朗日差值的函数double yy[12],lx[12],ly[12];double l_fenzi[12],l_fenmu[12];double l_x,l_y;for(i=0; i<=10; i++){yy[i]=1.0/(1+25*yx[i]*yx[i]);}for(i=0; i<=10; i++){l_fenmu[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenmu[i]=l_fenmu[i]*(yx[i]-yx[j]);}}double qq,pp;for(qq=-1; qq<=1; qq+=0.0003){for(i=0; i<=10; i++){l_fenzi[i]=1.0;for(j=0; j<=10; j++){if(i!=j)l_fenzi[i]=l_fenzi[i]*(qq-yx[j]);}}pp=0;for(i=0; i<=11; i++){pp=pp+1.0/(1+25*yx[i]*yx[i])*l_fenzi[i]/l_fenmu[i];}pDC->SetPixel(qq*500,pp*390+5,RGB(150,255,0));}}}3实验操作算法描述：先从特殊情况入手，研究线形插值和二次插值。
