数据结构总复习资料(完整版)
- 格式:doc
- 大小:42.00 KB
- 文档页数:21

数据结构期末复习*时间复杂度1. for (i=0; i<n; i++)for (j=0; j<m; j++)A[i][j]=0;答:O(m*n)2. s=0;for i=0; i<n; i++)for(j=0; j<n; j++)s+=B[i][j];sum=s;答:O(n2)3. x=0;for(i=1; i<n; i++)for (j=1; j<=n-i; j++)x++;解:因为x++共执行了n-1+n-2+……+1= n(n-1)/2,所以执行时间为O(n2)4. i=1;while(i<=n)i=i*3;答:O(log3n)5.for (i=1;i<n;i++){ y=y+1;for (j=0; j<=(2*n); j++)x++;}答:O(n2)6.x=1;for (i=1;i<=n;i++)for (j=1;j<=i;j++)for (k=1;k<=j;k++)x++;答:O(n3)*线性表的定义和性质,求地址的方法线性表的定义:是n个数据元素的有限序列线性表的性质:1、线性表中结点的集合是有限的,结点间的关系是一对一的。
2、(D)7. 线性表若采用链式存储结构时,要求内存中可用存储单元的地址:(A)必须是连续的(B)部分地址必须是连续的(C)一定是不连续的(D)连续或不连续都可以3、(B)8.线性表L在情况下适用于使用链式结构实现。
(A)需经常修改L中的结点值(B)需不断对L进行删除插入(C)L中含有大量的结点(D)L中结点结构复杂求地址的方法:设首元素a1的存放地址为LOC(a1)(称为首地址),设每个元素占用存储空间(地址长度)为L字节,则表中任一数据元素的存放地址为:LOC(ai) = LOC(a1) + L *(i-1)LOC(ai+1) = LOC(ai)+L*字符串相等的定义长度相等并且各个对应位置上的字符都相等。

数据结构复习资料复习提纲知识要点归纳数据结构复习资料:复习提纲知识要点归纳一、数据结构概述1. 数据结构的定义和作用2. 常见的数据结构类型3. 数据结构与算法的关系二、线性结构1. 数组的概念及其特点2. 链表的概念及其分类3. 栈的定义和基本操作4. 队列的定义和基本操作三、树结构1. 树的基本概念及定义2. 二叉树的性质和遍历方式3. 平衡二叉树的概念及应用4. 堆的定义和基本操作四、图结构1. 图的基本概念及表示方法2. 图的遍历算法:深度优先搜索和广度优先搜索3. 最短路径算法及其应用4. 最小生成树算法及其应用五、查找与排序1. 查找算法的分类及其特点2. 顺序查找和二分查找算法3. 哈希查找算法及其应用4. 常见的排序算法:冒泡排序、插入排序、选择排序、归并排序、快速排序六、高级数据结构1. 图的高级算法:拓扑排序和关键路径2. 并查集的定义和操作3. 线段树的概念及其应用4. Trie树的概念及其应用七、应用案例1. 使用数据结构解决实际问题的案例介绍2. 如何选择适合的数据结构和算法八、复杂度分析1. 时间复杂度和空间复杂度的定义2. 如何进行复杂度分析3. 常见算法的复杂度比较九、常见问题及解决方法1. 数据结构相关的常见问题解答2. 如何优化算法的性能十、总结与展望1. 数据结构学习的重要性和难点2. 对未来数据结构的发展趋势的展望以上是数据结构复习资料的复习提纲知识要点归纳。
希望能够帮助你进行复习和回顾,加深对数据结构的理解和掌握。
在学习过程中,要注重理论与实践相结合,多进行编程练习和实际应用,提高数据结构的实际运用能力。
祝你复习顺利,取得好成绩!。

数据结构复习资料.数据结构的定义数据结构是一门讨论“描述现实世界实体的数学模型(非数值计算)及其上的操作在计算机中如何表示和实现”的学科。
数据结构:是指数据以及数据元素相互之间的联系,可以看作是相互之间存在着某种特定关系的数据元素的集合。
对数据结构的内容包括以下几个方面:①数据的逻辑结构,指数据元素之间的逻辑关系。
②数据的存储结构,指数据元素及其关系在计算机存储器中的存储方式,也称为数据的物理结构。
③数据运算,指施加在数据上的操作。
算法是对特定问题求解步骤的一种描述,它是指令的有限序列,其中,每一条指令表示一个或多个操作。
粗略地说,算法是为了求解问题而给出的一个指令序列,程序是算法的一种具体实现。
一个算法必须满足以下五个重要特性:1. 有穷性2. 确定性3. 可行性4. 有输入5. 有输出算法的重要特征(1) 有穷性: 算法在有穷步之后结束,每一步在有穷时间内完成。
(2) 确定性: 算法中的每一条指令有明确的含义,无二义性。
(3) 可行性: 可通过已经实现的基本运算执行有限次来实现算法中的所有操作。
算法分析的两个主要方面是分析算法的时间复杂度和空间复杂度。
算法的执行时间主要与问题的规模有关。
问题规模是一个与输入有关的量。
语句频度是指算法中该语句被重复执行的次数。
算法中所有语句的频度之和记作T(n),是该算法所求解问题规模的函数。
当问题规模趋向无穷大时,T(n)的数量级称为渐进时间复杂度,简称时间复杂度,记作T(n)=O(f(n))。
通常采用算法中表示基本运算的语句的频度来分析算法的时间复杂度。
例题:1. 数据结构中的逻辑结构是指(),物理结构是指()。
2. 算法的基本特征包括有穷性、( )、( )、有输入和输出。
3. 算法的有穷性是指()。
4. 算法的确定性是指()。
5. 算法的可行性是指()。
6. 算法分析的两个主要方面是分析算法的()和空间复杂度。
7. 语句频度是指(算法中该语句被重复执行的次数)。


1、函数实现单链表得插入算法。
int ListInsert(LinkList L,int i,ElemType e){ LNode *p,*s;int j;p=L;j=0;while((p!=NULL)&&(j<i-1)){p=p->next;j++;}if(p==NULL||j>i-1) return ERROR;s=(LNode *)malloc(sizeof(LNode));s->data=e;s->next=p->next)p->next=sreturn OK;}/*ListInsert*/2、函数ListDelete_sq实现顺序表删除算法。
int ListDelete_sq(Sqlist *L,int i){int k;if(i<1||i>L->length) return ERROR;for(k=i-1;k<L->length-1;k++)L->slist[k]=L->slist[k+1]--L->Lengthreturn OK;}3、函数实现单链表得删除算法。
int ListDelete(LinkList L,int i,ElemType *s){LNode *p,*q;int j;p=L;j=0;while(( p->next!=NULL )&&(j<i-1)){p=p->next;j++;}if(p->next==NULL||j>i-1) return ERROR;q=p->next;p->next=q->next ;*s=q->data;free(q);return OK;}/*listDelete*/4、栈得基本操作函数:int InitStack(SqStack *S); //构造空栈int StackEmpty(SqStack *S);//判断栈空int Push(SqStack *S,ElemType e);//入栈int Pop(SqStack *S,ElemType *e);//出栈函数conversion实现十进制数转换为八进制数,请将函数补充完整。

第一章数据结构概述基本概念与术语1.数据:数据是对客观事物的符号表示,在计算机科学中是指所有能输入到计算机中并被计算机程序所处理的符号的总称。
2.数据元素:数据元素是数据的基本单位,是数据这个集合中的个体,也称之为元素,结点,顶点记录。
(补充:一个数据元素可由若干个数据项组成。
数据项是数据的不可分割的最小单位。
)3.数据对象:数据对象是具有相同性质的数据元素的集合,是数据的一个子集。
(有时候也叫做属性。
)4.数据结构:数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
(1)数据的逻辑结构:数据的逻辑结构是指数据元素之间存在的固有逻辑关系,常称为数据结构。
数据的逻辑结构是从数据元素之间存在的逻辑关系上描述数据与数据的存储无关,是独立于计算机的。
依据数据元素之间的关系,可以把数据的逻辑结构分成以下几种:1.集合:数据中的数据元素之间除了“同属于一个集合“的关系以外,没有其他关系。
2.线性结构:结构中的数据元素之间存在“一对一“的关系。
若结构为非空集合,则除了第一个元素之外,和最后一个元素之外,其他每个元素都只有一个直接前驱和一个直接后继。
3.树形结构:结构中的数据元素之间存在“一对多“的关系。
若数据为非空集,则除了第一个元素(根)之外,其它每个数据元素都只有一个直接前驱,以及多个或零个直接后继。
4.图状结构:结构中的数据元素存在“多对多”的关系。
若结构为非空集,折每个数据可有多个(或零个)直接后继。
(2)数据的存储结构:数据元素及其关系在计算机内的表示称为数据的存储结构。
想要计算机处理数据,就必须把数据的逻辑结构映射为数据的存储结构。
逻辑结构可以映射为以下两种存储结构:1.顺序存储结构:把逻辑上相邻的数据元素存储在物理位置也相邻的存储单元中,借助元素在存储器中的相对位置来表示数据之间的逻辑关系。
2.链式存储结构:借助指针表达数据元素之间的逻辑关系。
不要求逻辑上相邻的数据元素物理位置上也相邻。

《数据结构导论》复习资料课程代码:02142一、单项选择题1.一个栈的输入序列为123…n,若输出序列的第一个元素是n,输出第i(1<=i<=n)个元素是A.不确定 B.n-i+1 C.i D.n-i2.具有N个结点的二叉树的二叉链表结构中,指针域为NULL的数目应为A. N B.2N C.N+1 D.2N+13.栈S最多能容纳4个元素。
现有6个元素按A、B、C、D、E、F的顺序进栈, 问下列哪一个序列是可能的出栈序列?A.(E、D、C、B、A、F) B.(B、C、E、F、A、D)C.(C、B、E、D、A、F) D.(A、D、F、E、B、C)4.已知指针p所指结点不是尾结点,若在*p之后插入结点*s,则应执行下列哪一个操作?A.s->next = p; p-> next = s; B.s-> next = p->next; p-> next = s;C.s-> next = p-> next; p = s; D. p-> next = s; s-> next = p;5.设带头结点的单循环链表的头指针为head,则判断该链表是否为空的条件是A.head->next==head B.head->next==NULLC.head!=NULL D.head==NULL6.一个队列的输入序列是A,B,C,D,则该队列的输出序列是A.A,B,C,D B.B,C,D,AC.D,C,B,A D.C,D,B,A7.以行序为主序的二维数组a[3][5]中,第一个元素a[0][0]的存储地址是100,每个元素占2个存储单元,则a[1][2]的存储地址是A.100 B.108 C.114 D.1168.二叉树的中序遍历序列中,结点P排在结点Q之前的条件是A.在二叉树中P在Q的左边B.在二叉树中P在Q的右边C.在二叉树中P是Q的祖先D.在二叉树中P是Q的子孙9.有10个顶点的无向完全图的边数是A.11 B.45 C.55 D.9010.在带权有向图中求两个结点之间的最短路径可以采用的算法是A.迪杰斯特拉(Dijkstra)算法B.克鲁斯卡尔(Kruskal)算法C.普里姆(Prim)算法D.深度优先搜索(DFS)算法11.利用双向链表作线性表的存储结构的优点是A.便于单向进行插入和删除的操作B.便于双向进行插入和删除的操作C.节省空间D.便于销毁结构释放空间12.在闭散列表中,散列到同一个地址而引起的“堆积”问题是引起的。

目录目录 .................................................................................................................. 错误!未定义书签。
第一章绪论 ................................................................................................ 错误!未定义书签。
一、内容提要........................................................................................... 错误!未定义书签。
二、学习重点........................................................................................... 错误!未定义书签。
三、例题解析........................................................................................... 错误!未定义书签。
第二章线性表 ............................................................................................... 错误!未定义书签。
一、内容提要......................................................................................... 错误!未定义书签。
二、学习重点......................................................................................... 错误!未定义书签。
一、填空题1、栈的特点是先进后出(或后进先出),队列的特点是先进先出。
2、顺序表中逻辑上相邻的元素物理位置也相邻,单链表中逻辑上相邻的元素物理位置不相邻。
3、算法的5个重要特性是__________、__________、_________、___________、___________。
4、线性表、栈、队列都是线性结构,可以在线性表的任何位置插入和删除元素,对于栈只能在栈顶位置插入和删除元素,对于队列只能在队尾位置插入和只能在队头删除元素。
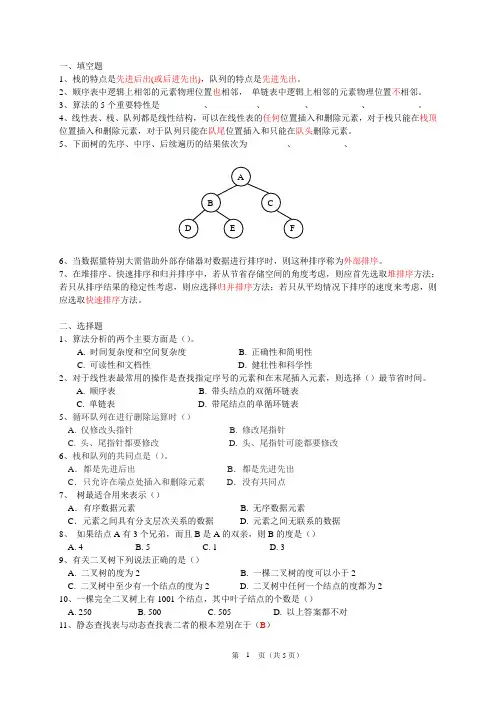
5、下面树的先序、中序、后续遍历的结果依次为_________、___________、__________6、当数据量特别大需借助外部存储器对数据进行排序时,则这种排序称为外部排序。
7、在堆排序、快速排序和归并排序中,若从节省存储空间的角度考虑,则应首先选取堆排序方法;若只从排序结果的稳定性考虑,则应选择归并排序方法;若只从平均情况下排序的速度来考虑,则应选取快速排序方法。
二、选择题1、算法分析的两个主要方面是()。
A. 时间复杂度和空间复杂度B. 正确性和简明性C. 可读性和文档性D. 健壮性和科学性2、对于线性表最常用的操作是查找指定序号的元素和在末尾插入元素,则选择()最节省时间。
A. 顺序表B. 带头结点的双循环链表C. 单链表D. 带尾结点的单循环链表5、循环队列在进行删除运算时()A. 仅修改头指针B. 修改尾指针C. 头、尾指针都要修改D. 头、尾指针可能都要修改6、栈和队列的共同点是()。
A.都是先进后出B.都是先进先出C.只允许在端点处插入和删除元素D.没有共同点7、树最适合用来表示()A.有序数据元素 B. 无序数据元素C.元素之间具有分支层次关系的数据 D. 元素之间无联系的数据8、如果结点A有3个兄弟,而且B是A的双亲,则B的度是()A. 4B. 5C. 1D. 39、有关二叉树下列说法正确的是()A. 二叉树的度为2B. 一棵二叉树的度可以小于2C. 二叉树中至少有一个结点的度为2D. 二叉树中任何一个结点的度都为210、一棵完全二叉树上有1001个结点,其中叶子结点的个数是()A. 250B. 500C. 505D. 以上答案都不对11、静态查找表与动态查找表二者的根本差别在于(B)A. 它们的逻辑结构不一样B. 施加在其上的操作不同C. 所包含的数据元素的类型不一样D. 存储实现不一样12、顺序查找法适合于存储结构为(B)的线性表。
数据结构总复习资料(完整版) 2018数据结构回顾 第1章简介 1.1数据结构的定义和分类 1。数据结构的定义 数据结构是一门研究计算机操作对象、它们之间的关系以及在非数值计算编程问题中的操作的学科
2。数据结构中包含的内容 (1)逻辑结构:数据元素之间的逻辑关系 (2)存储结构:计算机内存中数据元素及其关系的表示(3)操作:数据操作(检索、排序、插入、删除和修改)为什么 1.2学习数据结构 1。学习数据结构的功能 (1)计算机中的数值运算依赖于方程,而不是数值运算(如表、树、图等)。)依赖于数据结构(2)同一数据对象,用不同的数据结构表示,在运行效率上可能有明显的差异 (3)编程的本质是为实际问题选择一个好的数据结构和设计一个好的算法。然而,一个好的算法在很大程度上取决于描述实际问题的数据结构。 2。电话号码查询问题 (1)一个好的搜索算法取决于该表的结构和存储。(2)电话号码表的结构和存储方式决定了搜索(算法)的效率 1.3算法 1的概念和特点。算法 算法的概念和特征是由几条指令组成的有限序列,并且具有以下特征:(1)输入:具有0个或更多输入的外部量(2)输出:至少生成一个输出 (3)很差:必须限制每条指令的执行次数(4)确定性:每条指令的含义必须清晰明确(5)可行性:每条指令的执行时间是有限的。 2。算法和程序的区别 (1)一个程序可能不满足有限性,但算法必须 (2)程序中的指令必须是机器可执行的,并且算法没有这样的限制。 (3)如果用机器可执行语言描述,算法就是程序 1/62
1.4算法分析 1。时间复杂度 算法中基本运算的重复次数是问题规模n的函数,用T(n)表示。如果存在辅助函数f(n),使得当n接近无穷大时,T(n)/f(n)的极限值是不等于零的常数,那么f(n)是与T(n)数量级相同的函数T(n)=O(f(n)),O(f(n))是算法的渐近时间复杂度,缩写为时间复杂度。算法的效率由时间复杂度来衡量。 常用函数的时间复杂度按数量和增长率的升序排列:常数阶O(1) 对数阶O(log2n)线性阶O(n) 线性对数阶O(n log2n) 2 平方阶O(n) 3 立方阶O(n)... k k次幂O(n) n 次幂O(2) 2。空间复杂度
空间复杂度是算法在计算机中执行时所需存储空间的度量,记录为:S(n) = O(f(n)) 3。算法分析 的目的是选择合适的算法并改进算法 1.5例 例1: 为(I = 1;不精确= p; }否则如果(t-> next = = NULL){ t-> next = p;p->下一个=空;}否则{ p-> next = t-> next;t-> next = p;}} (3)删除 void(link list * head){ link list p,q;p = head while (p->next!=NULL){ if (p->数据!=p->下一个->数据)p=p->下一个;否则 { q = p-> next;p-> next = q-> next;自由(q);}}} (4)反向 无效反向(linklist * head) {linklist * s,* t,* p;p = heads = p->下一个; while(s->next!=空){ t = s->下一个;s-> next = p;p = s。s = t。} s-> next = p; 头->下一个->下一个=空;head-> next = s; 5/62
2.3示例 示例1:一维数组m,下标范围为0到9,每个数组元素存储有相邻的5个字节内存由字节寻址。如果存储阵列元件的第一个字节的地址是98,那么[3]的第一个字节的地址是113示例2:在长度为n的序列表中,当在第I个元素(1≤i≤n+1)之前插入新元素时,需要向后移动第n-i+1个元素(或者需要向前移动第n-i个元素以删除第I个元素) 示例3:如果*p节点不是单个链表中的结束节点,在它之前或之后插入*s节点或删除节点的操作是什么? 解决方案:在其前面插入*s节点:s-> next = p-> next;p-> next = s;t=p->数据;p->数据=s->数据;s->数据= t;在 之后,插入*s节点:s-> next = p-> next;p-> next = s;删除前一个节点:需要通过遍历 : q = p->next删除后一个节点;p-> next = q-> next;自由(q); 删除自己的节点:q = p-> next;p->数据= q->数据;p-> next = q-> next;自由(q); 例4:在以下线性表的存储结构中,读取指定序列号所需时间最少的元素是序列结构 第3章堆栈和队列 3.1堆栈和队列的基本概念 1。堆栈概念 堆栈是一个线性表,只允许在同一侧进行插入和删除操作允许插入和删除的一端称为栈顶,另一端称为栈底。当堆栈中没有数据元素时,它被称为空堆栈。它具有先进先出或后进先出的特点 2。堆栈
(1)顺序堆栈 typedef int数据类型的定义;#定义MAXSIZE 100 typedef结构{ 数据类型数据[MAXSIZE]; int top;} seqstack。seqstack * s;
(2)链接堆栈 typedef int数据类型;typedef结构节点{ 数据类型数据; 结构节点* next} linkstacklinkstack * top top是唯一确定链栈的栈顶指针当top =空时,链接栈为空链栈中的节点是动态生成的,没有考虑溢出问题。 3。顺序堆栈操作 (1)确定堆栈为空。s –>顶部> = 0); 6/62
} (2)空堆栈 void set null(seqtack * s){ s –> top =-1; } (3)判断堆栈已满 int full(seqtach * s){ return(s –> top = = maxsize-1); } (4)推入堆栈 seqtack * push (seqtack * s,data typex){ if(full(s)) { printf(“堆栈溢出”);返回空值;} s –> top ++;s –>数据[s –>顶部]= x; 返回s;(5)按下 datatype pop(seq tach * s){ if(空的)){ printf(“stack underflow”);返回空值; } –>顶部-; 年收益(s –>数据[s –>排名+1]); } (6)获取堆栈的顶部 data typetop(seqtach * s){ if(empty(s)){ printf(“堆栈为空”);返回空值; } 返回(s –>数据[s –>顶部]); } 4。链接栈操作
(1)推栈 链接栈*推栈(链接栈*顶部,数据类型X) { 链接栈* P; p =(link stack *)malloc(size of(link stack));p->数据= x;p->下一个=顶部; 返回p;/*返回新的堆栈顶部指针*/ } (2)堆栈外 LinkStack * PopStack(LinkStack * Top,数据类型* data){ 7/62
} LinkStack * p;if (top==NULL) { printf(“欠流”);返回空值;}数据=顶部->数据;/*堆栈的顶部节点数据存储在* data */p = top中; top = top-> next;免费(p); 9年返回顶部;/*返回新的堆栈顶部指针*/ 5。队列 队列的概念也是一个具有有限操作的线性表只允许在表的一端插入,允许在另一端删除。允许删除的一端称为前端,允许插入的一端称为后端。它具有先进先出的特点 6。队列
(1)顺序队列 #定义MaxSize 100 TypeDef结构{ DataType数据[MaxSize];内部阵线;内部后部;} sequeue sequeue * sq; (2)链队列 typedef structqueuenode { data type data; struct queue node * next;}队列节点;typedef结构{ QueueNode * front;队列节点*后部;}链接队列; 7。循环队列 (1)假溢出 在入队和出队操作期间,头指针和尾指针只增加而不减少,导致已删除元素的空间永远不会被重用虽然队列中元素的实际数量比向量空间的规模小得多,但尾部指针也有可能超出向量空间的上限,无法排队。这种现象被称为假溢出(2)循环队列 引入循环队列的概念来解决假溢出问题在循环队列中的队列输出和队列输入操作期间,头指针和尾指针仍然需要增加1才能向前移动。然而,当头指针和尾指针指向向量的上限(MaxSize-1)时,其加1运算的结果是指向向量的下限0 (3)当团队为空且已满时, 进入团队,尾部指针赶上头部指针。当离开队伍时,头指针追上尾指针。因此,当团队是空的和满的时候,头指针等于尾指针。无法通过sq-> front = = sq->原因来判断队列是空的还是满的 至少有两种方法来解决这个问题: 1,和另一个布尔变量来区分空队列和满队列; 2,以少一个元素空间为代价,在进入团队之前,测试尾部指针sq->