2013数学中考专题3(方案设计类)

2013年中考数学复习专题———提高解答题（一）1、分别把带有指针的圆形转盘A、B分成4等份、3等份的扇形区域，并在每一个小区域内标上数字（如图所示）．欢欢、乐乐两个人玩转盘游戏，游戏规则是：同时转动两个转盘，当转盘停止时，若指针所指两区域的数字之积为奇数，则欢欢胜；若指针所指两区域的数字之积为偶数，则乐乐胜；若有指针落在分割线上，则无效，需重新转动转盘．（1）试用列表或画树状图的方法，求欢欢获胜的概率；（2）请问这个游戏规则对欢欢、乐乐双方公平吗？试说明理由．2、已知二次函数2y x bx c=-++的图象如图所示，它与x轴的一个交点坐标为（－1，0），与y轴的交点坐标为（0，3）．⑴求出b，c的值，并写出此二次函数的解析式；⑵根据图象，写出函数值y为正数时，自变量x的取值范围．3、某品牌瓶装饮料每箱价格26元．某商店对该瓶装饮料进行“买一送三”促销活动，若整箱购买，则买一箱送三瓶，这相当于每瓶比原价便宜了0.6元．问该品牌饮料一箱有多少瓶？4、某学校组织340名师生进行长途考察活动，带有行礼170件，计划租用甲、乙两种型号的汽车共有10辆．经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．（1）请你帮助学校设计所有可行的租车方案；（2）如果甲车的租金为每辆2000元，乙车的租金为每辆1800元，问哪种可行方案使租车费用最省？5、如图，分别以R t A B C∆的直角边AC及斜边AB向外作等边A C D∆，等边ABE∆．已知∠BAC＝30°，EF⊥AB，垂足为F，连结DF．⑴试说明AC＝EF；⑵求证：四边形ADFE是平行四边形．6、如图，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路. 现新修一条路AC到公路l. 小明测量出∠ACD=30º，∠ABD=45º，BC=50m. 请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m；参考数据：414.12≈，732.13≈）.A。

2013中考数学专题训练：实数的运算、化简求值1. （2012黑龙江）计算：3202)1(2)330cos (-+--︒-π．2. （2012内蒙古）20sin 30(2)-︒+--；3. （2012青海）计算：)2152cos60++2π-⎛⎫-- ⎪⎝⎭4. （2012甘肃）计算：02112sin 30( 3.14)()2π---︒+-+5. （2012广西）计算：0201264sin 45(1)-+-．6. （2012广西）计算：|－3|＋2－1＋12(π－3)0－tan60°；7. （2012广西）计算：4cos45°＋(π＋3)0116-⎛⎫⎪⎝⎭。

8. （2012山东）计算：(113tan 60+13-⎛⎫--- ⎪⎝⎭9. （2012山东）计算：2012022(1)(3)(2)π--+-⨯--10. （2012贵州）计算：)()2201212sin 30+13π-⎛⎫---- ⎪⎝⎭11. （2012贵州）计算：)20111+2sin 602-⎛⎫---⎪⎝⎭12. （2012贵州）计算：0222214sin 60+3π⎛⎫---- ⎪⎝⎭．13. （2012四川）计算：()()120121312π-⎛⎫-⨯- ⎪⎝⎭14. （2012四川）计算：161)1(130sin )2(2+-+-+--o o π. 15. （2012四川）计算：-+-8)2012(04sin 1)21(45-+16. （2012四川）计算：01201211(1)883π-⎛⎫⎛⎫+-+- ⎪ ⎪⎝⎭⎝⎭17. （2012四川）计算：()00212sin 45+3014+2π---．18. （2012四川）计算：(()0204cos 45+1π-19. （2012湖南）计算：()()20121 3.142tan4511()2π-+--︒+-.20. （2012湖南）计算：()10132012+2cos303π-⎛⎫--- ⎪⎝⎭．21. （2012湖南）计算：()10120122+3tan 303π-⎛⎫-- ⎪⎝⎭． 22. （2012湖南）计算：010113tan 452π--++--（）（）23. （2012广东）计算：13160sin 2123-⎪⎭⎫⎝⎛++-- ．24. （2012广东）()111+20122π-⎛⎫--- ⎪⎝⎭． 25. （2012广东）计算： 45cos 8)13()21(|4|01---+-26. （2012重庆）计算：()()22012311-|5|2-π4-⎪⎭⎫ ⎝⎛++--+． 27. （2012黑龙江）先化简221x 4x 41x 1x 1+⎛⎫÷- ⎪⎝⎭---，再从0，－2，－1，1中选择一个合适的数代入并求值。

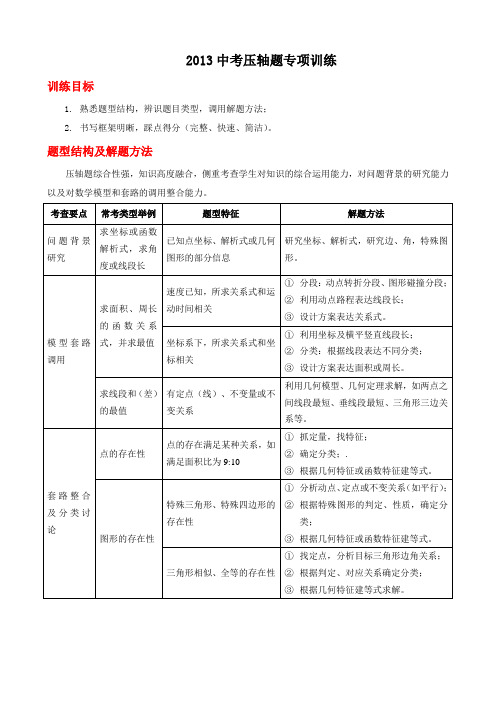
2013中考压轴题专项训练训练目标1.熟悉题型结构，辨识题目类型，调用解题方法；2.书写框架明晰，踩点得分（完整、快速、简洁）。

题型结构及解题方法压轴题综合性强，知识高度融合，侧重考查学生对知识的综合运用能力，对问题背景的研究能力以及对数学模型和套路的调用整合能力。

答题规范动作1.试卷上探索思路、在演草纸上演草。

2.合理规划答题卡的答题区域：两栏书写，先左后右。

作答前根据思路，提前规划，确保在答题区域内写完答案；同时方便修改。

3.作答要求：框架明晰，结论突出，过程简洁。

23题作答更加注重结论，不同类型的作答要点：几何推理环节，要突出几何特征及数量关系表达，简化证明过程；面积问题，要突出面积表达的方案和结论；几何最值问题，直接确定最值存在状态，再进行求解；存在性问题，要明确分类，突出总结。

4.20分钟内完成。

实力才是考试发挥的前提。

若在真题演练阶段训练过程中，对老师所讲的套路不熟悉或不知道，需要查找资源解决。

下方所列查漏补缺资源集中训练每类问题的思路和方法，这些训练与真题演练阶段的训练互相补充，帮学生系统解决压轴题，以到中考考场时，不仅题目会做，而且能高效拿分。

课程名称：2013中考数学难点突破之动点1、图形运动产生的面积问题2、存在性问题3、二次函数综合（包括二次函数与几何综合、二次函数之面积问题、二次函数中的存在性问题）3、2013中考数学压轴题全面突破（包括动态几何、函数与几何综合、点的存在性、三角形的存在性、四边形的存在性、压轴题综合训练）一、图形运动产生的面积问题一、 知识点睛 1. 研究_基本_图形 2. 分析运动状态：①由起点、终点确定t 的范围；②对t 分段，根据运动趋势画图，找边与定点，通常是状态转折点相交时的特殊位置． 3. 分段画图，选择适当方法表达面积． 二、精讲精练1. 已知，等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在△ABC 的边AB 上，沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M 、N 分别作AB 边的垂线，与△ABC 的其他边交于P 、Q 两点，线段MN 运动的时间为t 秒． （1）线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积． （2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．1题图 2题图2. 如图，等腰梯形ABCD 中，AB ∥CD ，AB＝ CD高CE＝，对角线AC 、BD 交于点H ．平行于线段BD 的两条直线MN 、RQ 同时从点A 出发，沿AC 方向向点C 匀速平移，分别交等腰梯形ABCD 的边于M 、N 和R 、Q ，分别交对角线AC 于F 、G ，当直线RQ 到达点C 时，两直线同时停止移动．记等腰梯形ABCD 被直线MN 扫过的面积为1S ，被直线RQ 扫过的面积为2S ，若直线MN 平移的速度为1单位/秒，直线RQ 平移的速度为2单位/秒，设两直线移动的时间为x 秒． （1）填空：∠AHB ＝____________；AC ＝_____________； （2）若213S S ，求x ．3. 如图，△ABC 中，∠C ＝90°，AC =8cm ，BC =6cm ，点P 、Q 同时从点C 出发，以1cm/s 的速度分别沿CA 、CB 匀速运动，当点Q 到达点B 时，点P 、Q 同时停止运动．过点P 作AC 的垂线l 交AB 于点R ，连接PQ 、RQ ，并作△PQR 关于直线l 对称的图形，得到△PQ'R ．设点Q 的运动时间为t （s ），△PQ'R 与△PAR 重叠部分的面积为S （cm 2）．（1）t 为何值时，点Q' 恰好落在AB 上？（2）求S 与t 的函数关系式，并写出t 的取值范围．（3）S 能否为98？若能，求出此时t 的值；若不能，请说明理由．CBAABCPRQ Q'l AC MNQPBCHD CBAA B CH HDCBA AB C DM N R QF G HE HD C BAHDCB A4.如图，在△ABC中，∠A=90°，AB=2cm，AC=4cm，动点P从点A出发，沿AB方向以1cm/s的速度向点B运动，动点Q从点B同时出发，沿BA方向以1cm/s的速度向点A运动．当点P到达点B时，P，Q两点同时停止运动．以AP为边向上作正方形APDE，过点Q作QF∥BC，交AC于点F．设点P的运动时间为t s，正方形APDE和梯形BCFQ重叠部分的面积为S cm2．（1）当t=_____s时，点P与点Q重合；（2）当t=_____s时，点D在QF上；（3）当点P在Q，B两点之间（不包括Q，B两点）时，求S与t之间的函数关系式．5.如图，在平面直角坐标系中，已知点A（0，1）、D（-2，0），作直线AD并以线段AD为一边向上作正方形ABCD．（1）填空：点B的坐标为________，点C的坐标为_________．（2）若正方形以每秒5个单位长度的速度沿射线DA向上平移，直至正方形的顶点C落在y轴上时停止运动．在运动过程中，设正方形落在y轴右侧部分的面积为S，求S关于平移时间t（秒）的函数关系式，并写出相应的自变量t的取值范围．l2与x轴相交于点N．（1）求M，N的坐标．（2）已知矩形ABCD中，AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动．设矩形ABCD与△OMN重叠部分的面积为S，移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）．求S与自变量t之间的函数关系式，并写出相应的自变量t的取值范围．A BCDNMOyA BC二、二次函数中的存在性问题一、知识点睛解决“二次函数中存在性问题”的基本步骤：①画图分析．研究确定图形，先画图解决其中一种情形．②分类讨论.先验证①的结果是否合理，再找其他分类，类比第一种情形求解．③验证取舍.结合点的运动范围，画图或推理，对结果取舍．二、精讲精练1.如图，已知点P是二次函数y=-x2+3x图象在y轴右侧．．部分上的一个动点，将直线y=-2x沿y轴向上平移，分别交x轴、y轴于A、B两点. 若以AB为直角边的△PAB与△OAB相似，请求出所有符合条件的点P的坐标．2.抛物线134y x=--+与y轴交于点A，顶点为B，对称轴BC与x轴交于点C．点P在抛物线上，直线PQ//BC交x轴于点Q，连接BQ．（1）若含45°角的直角三角板如图所示放置，其中一个顶点与点C重合，直角顶点D在BQ上，另一个顶点E在PQ上，求直线BQ的函数解析式；（2）若含30°角的直角三角板的一个顶点与点C重合，直角顶点D在直线BQ上（点D不与点Q重合），另一个顶点E在PQ上，求点P的坐标．3.如图，矩形OBCD的边OD、OB分别在x轴正半轴和y轴负半轴上，且OD＝10，OB＝8．将矩形的边BC绕点B逆时针旋转，使点C恰好与x轴上的点A重合．（1）若抛物线cbxxy++-=231经过A、B两点，求该抛物线的解析式：______________；（2）若点M是直线AB作MN⊥x轴于点N．是否存在点M，使△AMN与△ACD相似？若存在，求出点M的坐标；若不存在，说明理由．yOyxyyxO O xyyxOO xyxCOyBAxxA ByO C COyBAx4. 已知抛物线2=23y x x --经过A 、B 、C 三点，点P （1，k ）在直线BC ：y=x -3上，若点M 在x 轴上，点N 在抛物线上，是否存在以A 、M 、N 、P 为顶点的四边形为平行四边形？若存在，请求出点M 的坐标；若不存在，请说明理由．5. 抛物线2212-+=x x y 与y 轴交于点C ，与直线y =x 交于A (-2，-2)、B (2，2)两点．如图，线段MN 在直线AB上移动，且MN =M 的横坐标为m ，过点M 作x 轴的垂线与x 轴交于点P ，过点N 作x 轴的垂线与抛物线交于点Q ．以P 、M 、Q 、N 为顶点的四边形否为平行四边形？若能，请求出m 的值；若不能，请说明理由．三、二次函数与几何综合一、知识点睛“二次函数与几何综合”思考流程：整合信息时，下面两点可为我们提供便利：①研究函数表达式．二次函数关注四点一线，一次函数关注k 、b ； ②)关键点坐标转线段长．找特殊图形、特殊位置关系，寻求边和角度信息． 二、精讲精练1. 如图，抛物线y =ax 2-5ax +4（a ＜0）经过△ABC 的三个顶点，已知BC ∥x 轴，点A 在x 轴上，点C 在y轴上，且AC =BC ． （1）求抛物线的解析式．（2）在抛物线的对称轴上是否存在点M ，使|MA -MB |最大？ 若存在，求出点M 的坐标；若不存在，请说明理由．yB2. 如图，已知抛物线y =ax 2-2ax -b （a >0）与x 轴交于A 、B 两点，点A 在点B 的右侧，且点B 的坐标为(-1，0)，与y 轴的负半轴交于点C ，顶点为D ．连接AC 、CD ，∠ACD =90°． （1）求抛物线的解析式；（2）点E 在抛物线的对称轴上，点F 在抛物线上，且以B 、A 、F 、E 四点为顶点的四边形为平行四边形，求点F 的坐标．3. 如图，在平面直角坐标系中，直线3342y x =-与抛物线214y x bx c =-++交于A 、B 两点，点A 在x 轴上，点B 的横坐标为-8．（1）求该抛物线的解析式；（2）点P 是直线AB 上方的抛物线上一动点（不与点A 、B 重合），过点P 作x 轴的垂线，垂足为C ，交直线AB 于点D ，作PE ⊥AB 于点E ．设△PDE 的周长为l ， 点P 的横坐标为x ，求l 关于x 的函数关系式，并求出l 的最大值．4. 已知，抛物线212y ax ax b =-+经过A (-1，0)，C (2，32)两点，与x 轴交于另一点B ．（1）求此抛物线的解析式；（2）若抛物线的顶点为M ，点P 为线段OB 上一动点 （不与点B 重合），点Q 在线段MB 上移动，且∠MPQ =45°，设线段OP =x ，MQ=22y ，求y 2与x 的函数关系式， 并直接写出自变量x 的取值范围．5. 已知抛物线2y ax bx c =++的对称轴为直线2x =，且与x 轴交于A 、BA (1，0)，C (0，-3). （1）求抛物线的解析式；（2）若点P 在抛物线上运动（点P 异于点A），①如图1，当△PBC 的面积与△ABC 的面积相等时，求点P 的坐标； ②如图2，当∠PCB =∠BCA 时，求直线CP 的解析式．四、中考数学压轴题专项训练1.如图，在直角梯形OABC 中，AB ∥OC ，BC ⊥x 轴于点C ，A (1，1)，B (3，1)．动点P 从点O 出发，沿x 轴正方向以每秒1个单位长度的速度移动．过点P 作PQ ⊥OA ，垂足为Q ．设点P 移动的时间为t 秒（0<t <4），△OPQ 与直角梯形OABC 重叠部分的面积为S ．2.如图，抛物线2++=bx ax y 与x 轴交于A (-1，0)，B (4，0)两点，与y 轴交于点C ，与过点C 且平行于x 轴的直线交于另一点D ，点P 是抛物线上一动点． （1）求抛物线的解析式及点D 的坐标．（2）点E在x 轴上，若以A ，E ，D ，P 为顶点的四边形是平行四边形，求此时点P 的坐标． （3）过点P 作直线CD 的垂线，垂足为Q ．若将△CPQ 沿CP 翻折，点Q 的对应点为Q ′，是否存在点P ，使点Q ′恰好在x 轴上？若存在，求出此时点P 的坐标；若不存在，请说明理由．3.（11分）如图，已知直线12y x =-+与坐标轴交于A ，B 两点，以线段AB 为边向上作正方形ABCD ，过点A ，D ，C 的抛物线与直线的另一个交点为E ．（1）请直接写出C ，D 两点的坐标，并求出抛物线的解析式；（2AB 下滑，直至顶点D 落在x 轴上时停止，设正方形落在x 轴下方部分的面积为S ，求S 关于滑行时间t 的函数关系式，并写出相应自变量t 的取值范围；（3）在（2）的条件下，抛物线与正方形一起平移，同时停止，求抛物线上C ，E 两点间的抛物线弧所扫过的面积．4.（11分）如图，抛物线y =ax 2+bx +c 交x 轴于点A (-3，0)，点B (1，0)，交y 轴于点E (0，-3)．点C 是点A 关于点B 的对称点，点F 是线段BC 的中点，直线l 过点F 且与y 轴于点D ．（1）求抛物线的解析式；（2）点K 为线段AB 上一动点，过点K 作x 轴的垂线，交直 线CD 于点H ，交抛物线于点G ，求线段HG 长度的最大值； （3）在直线l 上取点M ，在抛物线上取点N ，使以A ，C ，M ， N 为顶点的四边形是平行四边形，求点N 的坐标．5.（11分）如图，在平面直角坐标系中，直线3342y x =-与 抛物线214y x bx c =-++交于A ，B 两点，点A 在x 轴上，点B （1）求抛物线的解析式．（2）点P 是直线AB 上方的抛物线上一动点（不与点A ，B 重合），过点P 作x 轴的垂线，垂足为C ，交直线AB 于点D ，作PE ⊥AB 于点E ．①设△PDE 的周长为l ，点P 的横坐标为x ，求l 关于x 的函数关系式，并求出l 的最大值． ②连接P A ，以P A 为边作图示一侧的正方形APFG ．随着点P 正方形的大小、位置也随之改变．当顶点F 或G 恰好落在y 直接写出对应的点P 的坐标．6.（11分）如图1，点A 为抛物线C 1：2122y x =-的顶点，点B 的坐标为 (1，0)，直线AB 交抛物线C 1于另一点C ． （1）求点C 的坐标；（2）如图1，平行于y 轴的直线x =3交直线AB 于点D ，交抛物线C 1于点E ，平行于y 轴的直线x =a 交直线AB 于点F ，交抛物线C 1于点G ，若FG :DE =4:3，求a 的值；（3）如图2，将抛物线C 1向下平移m （m >0）个单位得到抛物线C 2，且抛物线C 2的顶点为P ，交x 轴负半轴于点M ，交射线AB 于点N ，NQ ⊥x 轴于点Q ，当NP 平分∠MNQ 时，求m 的值．附：参考答案一、图形运动产生的面积问题1. （1）当t =32时，四边形MNQP 恰为矩形．此时，该矩形的面积为2平方厘米．（2） 当0＜t ≤1时，+2S =；当1＜t ≤2时，2S =；当2＜t ＜3时，S = 2．（1）90°；4 （2）x =2.3．（1）当t =125时，点Q' 恰好落在AB 上. （2）当0＜t ≤125时，23-+38S t t =；当125＜t ≤6时，29(8-)56S t =（3）由（2）问可得，当0＜t ≤125时，239-388t t += ；当125＜t ≤6时，299(8-)568t =；解得，8t =4t =98S =.4．（1）1 （2）45（3）当1＜t ≤43时，29-24S t t =；当43＜t ＜2时，29-10-84S t t =+.5．（1）（﹣1，3），（﹣3，2） （2）当0＜t ≤12时，25S t =；当12＜t ≤1时，55-4S t =；当1＜t ≤32时，225-515-4S t t =+.6．（1）M （4，2） N （6，0）（2）当0≤t ≤1时，24t S =；当1＜t ≤4时，1-24t S =； 当4＜t ≤5时，231349--424S t t =+；当5＜t ≤6时，13-2S t =+；当6＜t ≤7时，()217-2S t =二、二次函数中的存在性问题1.解：由题意，设OA =m ，则OB =2m ；当∠BAP =90°时， △BAP ∽△AOB 或△BAP ∽△BOA ； ① 若△BAP ∽△AOB ，如图1，可知△PMA ∽△AOB ，相似比为2：1；则P 1（5m ，2m ），代入x x y 32+-=，可知2513=m ，)2526,513(1P ② 若△BAP ∽△BOA ，如图2，可知△PMA ∽△AOB ，相似比为1：2；则P 2（2m ，2m），代入x x y 32+-=，可知811=m ，)1611,411(2P当∠ABP =90°时，△ABP ∽△AOB 或△ABP ∽△BOA ； ③ 若△ABP ∽△AOB ，如图3，可知△PMB ∽△BOA ，相似比为2：1；则P 3（4m ，4m ）， 代入x x y 32+-=，可知21=m ，)2,2(3P ④ 若△ABP ∽△BOA ，如图4，可知△PMB ∽△BOA ，相似比为1：2；则P 4（m ，m 25）， 代入x x y 32+-=，可知21=m ，415(,)24P2.解：（1）由抛物线解析式()21134y x =--+可得B 点坐标（1，3）要求直线BQ 的函数解析式，只需求得点Q 坐标即可，即求CQ 长度. 过点D 作DG ⊥x 轴于点G ，过点D 作DF ⊥QP 于点F . 则可证△DCG ≌△DEF .则DG =DF ，∴矩形DGQF 为正方形.则∠DQG =45°，则△BCQ 为等腰直角三角形.∴CQ =BC=3，此时，Q 可得BQ 解析式为y =－x +4.（2）要求P 点坐标，只需求得点Q 坐标，然后根据横坐标相同来求点P 坐标即可. 而题目当中没有说明∠DCE =30°还是∠DCE =60°，所以分两种情况来讨论. ① 当∠DCE =30°时，a ）过点D 作DH ⊥x 轴于点H ，过点D 作DK ⊥QP 于点K . 则可证△DCH ∽△DEK .则DH DCDK DE== 在矩形DHQK 中，DK =HQ ，则DHHQ=在Rt △DHQ 中，∠DQC =60°.则在Rt △BCQ 中，BCCQ=∴CQ ，此时，Q 点坐标为（）则P 点横坐标为代入()21134y x =--+可得纵坐标.∴P （b ）又P 、Q 为动点，∴可能PQ 由对称性可得此时点P 坐标为（194）② 当∠DCE =60°时，a) 过点D 作DM ⊥x 轴于点M ，过点D 作DN ⊥QP 于点N .则可证△DCM ∽△DEN .则DM DC DN DE == 在矩形DMQN 中，DN =MQ ，则DM MQ =. 在Rt △DMQ 中，∠DQM =30°.则在Rt △BCQ 中，BC CQ =∴CQ =Q 点坐标为（1+0） 则P 点横坐标为1+代入()21134y x =--+可得纵坐标.∴P （b ）又P 、Q 为动点，∴可能PQ 在对称轴左侧，与上一种情形关于对称轴对称.由对称性可得此时点P 坐标为（1－154－） 综上所述，P 点坐标为（94），（194），（1+154－）或（1－154－）.当2=ANMN 时，268310312=-+-m m m ，即264631=---mm m ))(( ∴2-=m （舍）2）如果点M 在x 轴上方的抛物线上：当21=AN MN 时，2168310312=--+-m m m ，即2164631=----m m m ))(( ∴211=m ∴M ),(41211 此时41=MN ,21=AN ∴21=AN MN ∴△AMN ∽△ACD ∴M ),(41211满足要求当2=ANMN 时，268310312=--+-m m m ，即264631=----mm m ))(( ∴m =10（舍） 综上M 1),(4725-,M 2),(412114.解：满足条件坐标为：1(36,0)-M 2(36,0)+M 3(12,0)-+M 4(12,0)--M 思路分析：A 、M 、N 、P 四点中点A 、点P 为顶点，则AP 可为平行四边形边、对角线； (1)如图，当AP 为平行四边形边时，平移AP ；∵点A 、P 纵坐标差为2 ∴点M 、N 纵坐标差为2； ∵点M 的纵坐标为0 ∴点N 的纵坐标为2或-2 ①当点N 的纵坐标为2时 解：2232--=x x 得16=±x又∵点A 、P 横坐标差为2 ∴点M 的坐标为： 1(36,0)-M 、2(36,0)+M ②当点N 的纵坐标为-2时解：2232--=-x x 得12=±x又∵点A 、P 横坐标差为2 ∴点M 的坐标为： 3(12,0)-+M 、4(12,0)--M (2)当AP 为平行四边形边对角线时； 设M 5（m ,0） MN 一定过AP 的中点（0，-1）则N 5（-m ，-2），N 5在抛物线上 ∴2232+-=-m m12=-±m （负值不符合题意，舍去）∴12=-+m ∴5(12,0)-+M 综上所述:符合条件点P 的坐标为：1(36,0)-M 2(36,0)+M 3(12,0)-+M 4(12,0)--M5．解：分析题意，可得：MP ∥NQ ，若以P 、M 、N 、Q 为顶点的四边形为平行四边形，只需MP =NQ 即可。

专题五方案设计专题【考纲与命题规律】考纲要求方案设计问题是运用学过的技能和方法，进行设计和操作，然后通过分析计算，证明等，确定出最佳方案的数学问题，一般涉及生产的方方面面，如：测量，购物，生产配料，汽车调配，图形拼接，所用到的数学知识有方程、不等式、函数解直角三角形，概率和统计等知识.命题规律方案设计问题应用性比较强，解题时要注重综合应用转化思想，数形结合的思想，方程函数思想及分类讨论等各种数学思想.【课堂精讲】例1.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注：不同的分法,面积可以相等)分析：（1）正方形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点，连接HE、EF、FG、GH、HF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可．（2）正方形ABCD中，E、F分别是AB、BC的中点，O是AC、BD的交点，连接OE、OF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可．（3）正方形ABCD中，F、H分别是BC、DA的中点，O是AC、BD的交点，连接HF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可．（4）正方形ABCD中，E、F分别是AB、BC的中点，O是AC的中点，I是AO的中点，连接OE、OB、OF，即可把正方形纸片恰好剪成六个等腰直角三角形；然后根据三角形的面积公式，求出分割后得到的最小等腰直角三角形面积即可．解答：根据分析，可得。

(1)第一种情况下，分割后得到的最小等腰直角三角形是△AEH、△BEF、△CFG、△DHG，每个最小的等腰直角三角形的面积是：(4÷2)×(4÷2)÷2=2×2÷2=2(cm2)(2)第二种情况下，分割后得到的最小等腰直角三角形是△AEO、△BEO、△BFO、△CFO，每个最小的等腰直角三角形的面积是：(4÷2)×(4÷2)÷2=2×2÷2=2(cm2)(3)第三种情况下，分割后得到的最小等腰直角三角形是△AHO、△DHO、△BFO、△CFO，每个最小的等腰直角三角形的面积是：(4÷2)×(4÷2)÷2=2×2÷2=2(cm2)(4)第四种情况下，分割后得到的最小等腰直角三角形是△AEI、△OEI，每个最小的等腰直角三角形的面积是：(4÷2)×(4÷2)÷2÷2=2×2÷2÷2=1(cm2).例2.甲乙两家商场平时以同样的价格出售相同的商品。

增城市2013年初中毕业班综合测试数学评分标准一、选择题（本题有10个小题，每小题3分，满分30分）二、填空题（本题有6个小题，每小题3分，共18分）三、解答题（本题有9个小题，共102分，解答要求写出文字说明、证明过程或计算步骤．）17．（本题满分9分）解：解不等式02 -x 得2 x ………………………………………………2分解不等式062 +-x 得3 x …………………………………………4分 ∴原不等式组的解集是32 x …………………………………………6分 解集在数轴上正确表示 ………………………………………………9分18．（本题满分9分）证明：∵四边形ABCD 是平行四边形∴BC AD //，BC AD =……………………………4分 ∴BCE DAF ∠=∠ …………………………6分 ∵CE AF =∴ADF ∆≌CBE ∆ ………………………7分 ∴DF BE = ……………………………9分BC18题图19．（本题满分10分）解：（1）∵AB 与⊙O 相切于点C∴AB OC ⊥ (3)分 ∵OA OB =∴4==BC AC (5)分在BOC Rt ∆中，4,2==BC OC 由勾股定理，得OB == ………………………7分（2）在AOC Rt ∆中，∵2,52===OC OB OA∴A sin =OC OA ==………………………10分 20．（本题满分10分） 解：∵032≠=ba ∴0,0,32≠≠=b a a b ………………………3分原式()()()b a b a b a ba 22225-∙-+-=………………………5分ba ba 225+-=………………………7分 ∵0,32≠=a a b ∴原式2142335==+-=a a a a a a ………………………10分 21．（本题满分12分）解：（1）总人数：()人200%2040=÷ ………………2分 补全图略 …………………4分（2）乒乓球占四项球类的百分比是：%30%10020060=⨯ 排球占四项球类的百分比是%10%20%30%401=--- ∴扇形统计图中喜欢排球的圆心角度数︒=︒⨯36360%10 (8)分 （3）列表法或树形图 (10)分总有20种等可能性结果，其中抽到一男一女的情况有12种，所以抽到一男一女的概率为 ()532012==一男一女P …………………………12分 22. （本题满分12分） 解：（1）∵已知反比例函数ky x=经过点(1,4)A k -+， ∴41kk -+=，即4k k -+=………………………1分 ∴2k = ………………………2分∴反比例函数的表达式为2y x= ()2,1A ………3分 ∵一次函数y x b =+的图象经过点()2,1A ………………4分 ∴21b =+∴1b = ………………5分 ∴一次函数的表达式为1y x =+ …………6分（2）由12y x y x =+⎧⎪⎨=⎪⎩………………………7分消去y，得220x x +-= ………………………8分即(2)(1)0x x +-=,∴2x =-或1x =∴1y =-或2y = ∴21x y =-⎧⎨=-⎩或12x y =⎧⎨=⎩………………………9分 ∵点B 在第三象限，∴点B 的坐标为B (21)--，……10分 由图象可知，当反比例函数的值大于一次函数的值时，x 的取值范围是2x <-或01x << ……………12分23. （本题满分12分）解：（1）设今年三月份甲种电脑每台售价x 元，根据题意得： (1)分100000800001000x x =+………………………2分解得：4000x =经检验：4000x =是所列方程的根 ………………………3分答：甲种电脑今年每台售价4000元． ...........................4分 （2）设购进甲种电脑x 台，根据题意得： (5)分4800035003000(15)50000x x +-≤≤ ………………………6分解得610x ≤≤ ………………………7分∴x 的正整数解为6，7，8，9，10，答：共有5种进货方案 ...........................8分 （3）设总获利为W 元，依题意得 (9)分(40003500)(38003000)(15)(300)1200015W x a x a x a =-+---=-+-……………10分当300a =时，（2）中所有方案获利相同． ........................11分 此时，购买甲种电脑6台，乙种电脑9台时对公司更有利． (12)分答：当300a =时，（2）中所有方案获利相同．此时，购买甲种电脑6台，乙种电脑9台时对公司更有利．24．（本题满分14分）（1）证明：∵b=2a ，点M 是AD 的中点………………………1分∴AB=AM=MD=DC=a………………………2分又∵在矩形ABCD 中，∠A=∠D=90°∴∠AMB=∠DMC=45° ………………………3分∴∠BMC=90°………………………4分（2）解：存在 ………………………5分证明：若∠BMC=90°则∠AMB=∠DMC=90° ∵∠AMB+∠ABM=90° ∴∠ABM=∠DMC ∵∠A=∠D=90° ∴△ABM ∽△DMC………………………6分∴=设AM=x ，则xb aa x -= ………………………7分 整理得：022=+-a bx x ∵b ＞2a ，a ＞0，b ＞0，∴ 0422a b -=∆∴方程有两个不相等的实数根，且两根均大于零，符合题意……8分∴当b ＞2a 时，存在∠BMC=90° ………………………9分（3）解：不成立． ………………………10分理由：若∠BMC=90°由（2）可知022=+-a bx x………………………12分∵b ＜2a ，a ＞0，b ＞0 ∴0422a b -=∆ ∴方程没有实数根………………………13分∴当b ＜2a 时，不存在∠BMC=90°，即（2）中的结论不成立．…………14分25．（本题满分14分）解：（1）(03)C ，………………………………………………2分（2） 抛物线2y x bx c =++过点B C ，，9303b c c ++=⎧∴⎨=⎩，．…………………………………………4分 解得43b c =-⎧⎨=⎩，． …………………………………………5分 ∴抛物线的解析式为243y x x =-+． …………………6分∴对称轴为2x = ……………………………………7分点(1)A ，0 …………………………………………8分（3）由243y x x =-+．可得(21)(10)D A -，，，． 3OB ∴=，3OC =，1OA =，2AB =．可得OBC △是等腰直角三角形．45OBC ∴∠=，CB =．…………………………………9分如图，设抛物线对称轴与x 轴交于点F，112AF AB ∴==． 过点A 作AE BC ⊥于点E ．90AEB ∴∠= ．可得BE AE ==CE = ………………………………10分在AEC △与AFP △中，90AEC AFP ∠=∠= ，ACE APF ∠=∠，AEC AFP ∴△∽△AE CE AF PF ∴=，1PF=．AEC AFP ∴△∽△ 解得2PF =………………………………………………12分点P 在抛物线的对称轴上，∴点P 的坐标为(22)，或(22)-，．……………………………………14分。

2013年中考专题复习——数与式（附答案）学校:___________姓名：___________班级：___________考号：___________一、选择题1．对有理数a 、b ，有如下的判断：（ ）（1）若︱a ︱=︱b ︱，则a=b. （2）若a=-b ，则2)(a -= b 2（3）若︱a ︱﹥b ，则︱a ︱﹥︱b ︱（4）若︱a ︱﹤︱b ︱，则a ﹤b其中正确的个数（ ）A 、1B 、2C 、3D 、42．绝对值大于2而小于5的所有正整数之和为（ ）A 、7B 、8C 、9D 、103．下列各数中，最小的数是（ ）A ．-2B ．0C ．21D ．2 4．若4a b +=，则222a ab b ++的值为（ ）A 、8B 、16C 、2D 、45．下列各对数不．是互为倒数的是（ ） A 、－1与－1 B 、2.5与52 C 、53-与35- D 、2与21- 6．估算348+的值（ ）A 、在7和8间B 、在8和9之间C 、在9和10之间D 、在10和11之间7．大于-2.5小于3的整数有（ ）个A 、3个B 、4个C 、5个D 、6个8．下列说法错误的是（ ）A ．81的平方根是3±B ．（-1）2010是最小的正整数C ．两个无理数的和一定是无理数D ．实数与数轴上的点一一对应9．下列等式不成立的是（ ）A 、66326=⋅B 、428=÷C 、D 、228=-10．2010年我国总人口约为l 370 000 000人，该人口数用科学记数法表示为（ ）A ．110.13710⨯B ．91.3710⨯C ．813.710⨯D ．713710⨯ 二、填空题11．定义一种运算：x ※y=))((y x y x -+，如：4※3=（4+3）（4-3）=7，则3※（5※4）= 。

12．一个数的平方等于这个数的立方，这个数是________.13．估算13的近似值等于 ．（精确到十分位）14．._____________x 5-3_____,__________x 5-3的差是与的和是与x x15．11的相反数为 ．16．某地12月中旬的一天中午气温为－5℃，晚6时气温下降了8℃，则晚6时气温为 __ ____℃．三、计算题 17．先化简，再求值：)3123()31(22122y x y x x +-+--，其中x=1，y=－118．（1）求x 值： 2542=x（2）求x 值：027.0)7.0(3=-x四、解答题19．小明在计算A-2（ab+2bc-4ac ）时，由于马虎，将“A -”写成了“A+”，得到的结果是3ab-2ac+5bc 。

2013北京中考数学压轴题训练（三）答案 2013.3.1354、B 55、B 603 63n + 56、C 57．A 58、1000 59、．2n －160、证明略 361、解：(1)因为y ＝ax 2－2amx ＋am 2＋2m ＋1＝a (x －m )2＋2m ＋1，所以抛物线C 1的顶点为A (m ，2m ＋1)．(2)如图，因为点A 、B 关于点P (1，3)成中心对称，作PE ⊥y 轴于点E ，作AF ⊥y 轴于点F ，可知△BPE ∽△BAF ．所以AF ＝2PE ，即m ＝2．又P (1，3)，A (2，5)，设直线AP 的解析式为y ＝kx ＋b ，把A 、P 的坐标代入得⎩⎨⎧+=+=.3,25b k b k所以k ＝2，b ＝1．故直线AB 的解析式是y ＝2x ＋1，得抛物线C 2的顶点的坐标是B (0，1)．因为C 1、C 2关于点P 成中心对称，所以抛物线的开口大小相同，方向相反，得C 2的解析式是y ＝－ax 2＋1．(3)在Rt △ABF 中，因为AB ＝2242+＝25＜5，所以不存在AB ＝AC 的情况． 当△ABC 为等腰三角形时，只有以下两种情况：第24题答图① 第24题答图② 第24题答图③①如图②，设C (x ，0)，若BC ＝AB ＝25，则1922=-=OB BC OC ，得C (19，0)．又C (19，0)在抛物线y ＝－ax 2＋1上，则191=a ． ②如图③，若AC ＝BC ，设C (x ，0)，作AD ⊥x 轴于点D ．在Rt △OBC 中，BC 2＝x 2＋1．在Rt △ADC 中，AC 2＝(x －2)2＋25．由x 2＋1＝(x －2)2＋25，解得x ＝7．因为C (7，0)在抛物线y ＝－ax 2＋1上，所以491=a ． 综上，使△ABC 是等腰三角形的a 的值有两个：1911=a ，4912=a ．62．(1)证明：∵六边形ABCDEF 为正六边形，∴每个内角均为120°．∵∠FMH ＝120°，A 、M 、B 在一线上，∴∠AFM ＋∠FMA ＝∠FMA ＋∠BMH ＝60°∴∠AFM ＝∠BMH ．(2)解：猜想：FM ＝MH ．证明：①当点M 与点A 重合时，∠FMB ＝120°，MB 与BQ 的交点H 与点B 重合，有FM ＝MH ．②当点M 与点A 不重合时，证法一：如图①，连结FB 并延长到G ，使BG ＝BH ，连结MG ．∵∠BAF ＝120°，AF ＝AB ，∴∠AFB ＝∠FBA ＝30°．⎪⎩⎪⎨⎧=∠=∠=,,,MB MB MBG MBH BG BH ∴△MBH ≌△MBG ．∴∠MHB ＝∠MGB ，MH ＝MG ．∵∠AFM ＝∠BMH ，∠HMB ＋∠MHB ＝30°，∴∠AFM ＋∠MGB ＝30°．∵∠AFM ＋∠MFB ＝30°，∴∠MFB ＝∠MGB ．∴FM ＝MG ＝MH ．证法二：如图②，在AF 上截取FP ＝MB ，连结PM ．∵AF ＝AB ，FP ＝MB ，∴P A ＝AM ∵∠A ＝120°，∴ 30)120180(21=-⨯=∠APM ， 有∠FPM ＝150°．∵BQ 平分∠CBN ，∴∠MBQ ＝120°＋30°＝150°，有∠FPM ＝∠MBH ．由(1)知∠PFM ＝∠HMB ，∴△FPM ≌△MBH ．∴FM ＝MH ．63、C 64、32 65．二，三，六 66、(1)连结OB ．因为AC 是⊙O 的直径，AB 是弦且等于半径长．所以OA ＝OB ＝AB ．所以△AOB 为等边三角形．所以∠OAB ＝60°．因为∠BAC ＝2∠BAN ＝60°，所以∠BAN ＝30°．所以∠CAN ＝∠BAC ＋∠BAN ＝90°．所以AC ⊥MN ．又因为AC 为直径，所以MN 是⊙O 的切线．(2)连结AE ，OE ．由E 是的中点，可得∠BAE ＝∠ABE ＝15°．易证△ABE ≌△ADE ． 所以BE ＝DE ，∠EDA ＝15°．可证得∠BDE ＝60°．所以△BDE 是等边三角形．67．解：(1)AB ＝AC ．(2)方法一：作∠BAC 的平分线，过点B 作射线AB 的垂线，两线交于点O ．由图形的对称性可知圆心在∠BAC 的平分线上，点O 就是该圆的圆心．可测得AB 的长度．在Rt △AOB 中，∠BAO ＝60°，所以OB ＝AB ·tan60°＝3AB ，所以直径为23AB ．方法二：连结OC ，BC ，可证得△COB 是等边三角形．所以BC ＝OC ．可求得BC 的长度， 所以直径等于2BC ．68．解：(1)△APQ ∽△BCP ．(答案不唯一)(2)当P 为AB 中点时，有AQ ＋BC ＝CQ ．证明：连结CQ ，延长QP ，交CB 的延长线于点E ．可证△APQ ≌△BPE ．则AQ ＝BE ，PQ ＝PE ．又因为CP ⊥QE ，可得CQ ＝CE ，所以AQ ＋BC ＝CQ ．(3)当AD AQ 92=时，有PC ＝3PQ ． 证明：在正方形ABCD 中，∠A ＝∠B ＝90°，AD ＝BC ＝AB ．又因为直角三角板的顶点P 在边AB 上，所以∠1＋∠2＝180°－∠QPC ＝90°． 因为Rt △CBP 中，∠3＋∠2＝90°，所以∠1＝∠3．所以△APQ ∽△BCP ．所以BC AP BP AQ PC PQ ==．因为AB AD AQ 9292==， 所以ABAP AP AB AB =-92．所以AB AP 31=， 或AB AP 32=(不合题意，舍去)． 所以31===AB AP BC AP PC PQ ．所以PC ＝3PQ ． 69、D 70、B 71、0 72．373、(1)∵四边形OABC 是矩形，且DE ⊥OD ，∴∠1＋∠2＝90°,∠3＋∠2＝90°．∴∠1＝∠3．又∵∠OCD ＝∠B ＝90°，∴△OCD ∽△DBE ．BD CO BE CD =∴． ∴t ＝1时，221=BE ，∴BE ＝1．∴点E 的坐标为(3，1)． 设直线DE 的解析式为y ＝kx ＋b ，又点D 的坐标为(1，2)，∴直线DE 的解析式为2521+-=x y ． (2)由(1)得BD CO BE CD =，即t BE t -=32．232t t BE +-=∴． 349243)(21++-=⋅+=∴t t BC CO BE S ．自变量t 的取值范围是：0＜t ＜3． (3)存在t 的值，使得OE 的长取得最小值．因为Rt △OAE 的直角边OA 的长为定值，所以当Rt △OAE 的面积最小时，AE 的长最小，即OE 的长最小．而当Rt △ OAE 的面积最小时，就是梯形COEB 的面积最大时．由(2) 167523433494322+⎪⎭⎫ ⎝⎛--=++-=t t t S 可知， 当23=t 时满足此要求．此时，872=-=BE AE ．∴点E 的坐标为⎪⎭⎫ ⎝⎛87,3． 74、(1)y ＝kx ＋3经过点B (3，0)，∴可求出k ＝－1．由题意可知，点D 的坐标为(0，3)．∵抛物线y ＝－x 2＋bx ＋c 经过点B 和点D ，⎩⎨⎧=++-=.3,390c c b 解得⎩⎨⎧==.3,2c b∴抛物线的解析式为y ＝－x 2＋2x ＋3．(2)如图，可求顶点C 的坐标为(1，4)．由题意，可知∠ODB ＝45°．过点D 作此抛物线对称轴的垂线DG ，可知DG ＝CG ＝1，所以此时∠DCG ＝45°，则易知点F 的坐标为(1，2)．(3)存在这样的点P ，使得以点P 、C 、E 、F 为顶点的四边形是平行四边形．理由如下：由题意知PE ∥CF ，∴要使以点P 、C 、E 、F 为顶点的四边形是平行四边形，只要满足PE ＝CF ＝2即可．∵点P 在直线DB 上，∴可设点P 的坐标为(x ，－x ＋3)．∵点E在抛物线y ＝－x 2＋2x ＋3上，∴可设点E 的坐标为(x ，－x 2＋2x ＋3)．∴当－x ＋3－(－x 2＋2x ＋3)＝2时， 解得2173±=x ； 当－x 2＋2x ＋3－(－x ＋3)＝2时，解得x ＝1或x ＝2，x ＝1不合题意，舍去．∴满足题意的点P 的横坐标分别为21731+=x ，21732-=x ，x 3＝2．75、D 76．B77、(1)证明：如图，连结OD ，∵△ABC 为等边三角形，DF ⊥AC ，∴∠ADF ＝30°，∵OB ＝OD ，∠DBO ＝60°，∴∠BDO ＝60°．∴∠ODF ＝180°－∠BDO －∠ADF ＝90°．∴DF 是⊙O 的切线．(2)解：∵AD ＝BD ＝2，∠ADF ＝30°，∴AF ＝1．∴FC ＝AC －AF ＝3．∵FH ⊥BC ，∴∠FHC ＝90°．在Rt △FHC 中，FC FHFCH =∠sin ，23360sin ==∴⋅ FC FH ．即FH 的长为233． 78、解：(1)由图象可知A (1，0)，B (4，6)，代入y ＝ax 2＋bx ＋2．得⎩⎨⎧++=++=.24166,20b a b a 解得⎩⎨⎧-==.3,1b a ∴抛物线的解析式为y ＝x 2－3x ＋2．(2)原抛物线的解析式可配方为41232-⎪⎭⎫ ⎝⎛-=x y ，抛物线向左平移1个单位长度后解析式为41212-⎪⎭⎫ ⎝⎛-=x y ，设向上或向下平移h 个单位长度， 则解析式为h x y +-⎪⎭⎫ ⎝⎛-=41212． 由A 、B 两点坐标可求得直线AB 的解析式为y ＝2x －2，由⎪⎩⎪⎨⎧-=+-⎪⎭⎫ ⎝⎛-=,22,41212x y h x y得2241212-=+-⎪⎭⎫ ⎝⎛-x h x ，化简得x 2－3x ＋h ＋2＝0， ∵抛物线与直线只有一个交点，即此一元二次方程只有唯一的根，∴b 2－4ac ＝0，即9－4×(h ＋2)＝0． 41=∴h ，也就是抛物线再向上平移41个单位长度能与直线AB 只有一个交点， 此时抛物线的解析式为221⎪⎭⎫ ⎝⎛-=x y ． (3)抛物线221⎪⎭⎫ ⎝⎛-=x y 向右平移25个单位长度，再向下平移t 个单位长度， 解析式为y ＝(x －3)2－t ．令y ＝0，即(x －3)2－t ＝0，则x 1＝3＋t ，x 2＝3－t ．由(2)知：点P (0，－2)． ∵过M 、N 、P 三点的圆的圆心一定在直线x ＝3上，点P 为定点，∴要使圆的面积最小，圆的半径应等于点P 到直线x ＝3的距离，此时，半径为3，面积为9π ．设圆心为C ，MN 的中点为E ，连结CE ，CM ．在三角形CEM 中，∵ME 2＋CE 2＝CM 2，∴(t )2＋22＝32，∴t ＝5．∴当t ＝5时，过M 、N 、P 三点的圆的面积最小，最小面积为9π ．79．解：(1)EG ＝CG ．证明：∵∠DEF ＝∠DCF ＝90°，DG ＝GF ，CG DF EG ==∴21． (2)(1)中结论成立，即EG ＝CG ．证明：过点F 作BC 的平行线，交DC 的延长线于点M ，连结MG ．∴EF ＝CM ，易证四边形EFMC 为矩形．∴∠EFG ＝∠GDM ．在直角三角形FMD 中，DG ＝GF ，∴FG ＝GM ＝GD ． 第79题答图① ∴∠GMD ＝∠GDM ．∴∠EFG ＝∠GMD ．∴△EFG ≌△CMG ．∴EG ＝CG ．(3)成立．证明：取BF 的中点H ，连结EH ，GH ，取BD 的中点O ，连结OG ，OC ．∵OB ＝OD ，∠DCB ＝90°，BD CO 21=∴．∵DG ＝GF ，BH ＝HF ，OD ＝OB ，∴GH ∥BO ，且BD GH 21=；OG ∥BF ,且BF OG 21=∴CO ＝GH ． ∵△BEF 为等腰直角三角形，BF EH 21=∴．∴EH ＝OG ． ∵四边形OBHG 为平行四边形，∴ ∠BOG ＝∠BHG ．∵∠BOC ＝∠BHE ＝90°，∴∠GOC ＝∠EHG ．∴△GOC ≌△EHG ．∴EG ＝GC ．第79题答图②80、D 81．B 82．①②③ 83．(－502，－502)84、解：(1)设二次函数的解析式为y ＝a (x －2)2＋m ，∵抛物线经过点(0，3)和(－1，8)，⎩⎨⎧+=+=∴.98,43m a m a 解得⎩⎨⎧-==,1,1m a ∴二次函数的解析式为y ＝(x －2)2－1＝x 2－4x ＋3． (2)抛物线y ＝x 2－4x ＋3与戈轴的交点为B (3，0)、C (1，0)，顶点为P (2，－1)． 由题意，设平移后直线为y ＝x ＋b ．由已知得，－1＝2＋b ，解得b ＝－3．∴直线y ＝x 平移后经过点P 的直线为y ＝x －3．当x ＝3时，y ＝0．∴直线y ＝x －3经过点B (3，0)．(3)能，点D 的坐标为(2，2)，理由如下：如图，过点D作DM ⊥x 轴于点肘，过点P 作PN ⊥x 轴于点N ．在Rt △ONP 中，OP 2＝ON 2＋PN 2＝5．∵点D 在直线y ＝x 上，∴设点D 的坐标为(x ，x )．在Rt △BDM 中，BD 2＝BM 2＋DM 2＝(3－x )2＋x 2．由OP 2＝BD 2得(3－x )2＋x 2＝5．解得x 1＝2，x 2＝1．当x ＝1时，四边形OPBD 为平行四边形，舍去．∴x ＝2．∴点D 的坐标为(2，2)．85．解：(1)EG ＝CG 且EG ⊥CG ．证明如下：如图①，连结BD ．∵正方形ABCD 和等腰Rt △BEF ，∴∠EBF ＝∠DBC ＝45°．∴B 、E 、D 三点共线． ∵∠DEF ＝90°，G 为DF 的中点，∠DCB ＝90°，∴EG ＝DG ＝GF ＝CG ．∴∠EGF ＝2∠EDG ，∠CGF ＝2∠CDG ．∴∠EGF ＋∠CGF ＝2∠EDC ＝90°， 即∠EGC ＝90°，∴EG ⊥CG ．(2)仍然成立，证明如下：如图②，延长EC 交CD 于点H ．∵BE ⊥EF ，∴EF ∥CD ，∴∠1＝∠2． 又∵∠3＝∠4，FG ＝DG ，∴△FEG ≌△DHG ，∴EF ＝DH ，EG ＝GH ．∵△BEF 为等腰直角三角形，∴BE ＝EF ，∴BE ＝DH ．∵CD ＝BC ,∴CE ＝CH ． ∴△ECH 为等腰直角三角形．又∵EG ＝GH ，∴EG ＝CG 且EG ⊥CG ．(3)仍然成立．证明如下：如图③，延长CG 至H ，使GH ＝CG ，连结HF 交BC 于M ，连结EH 、EC ． ∵GF ＝GD ，∠HGF ＝∠CGD ，HG ＝CG ，∴△HFG ≌△CDG ，∴HF ＝CD ，∠GHF ＝∠GCD ，∴HF //CD ．∵正方形ABCD ，∴HF ＝BC ，HF ⊥BC ． ∵△BEF 是等腰直角三角形，∴BE ＝EF ，∠EBC ＝∠HFE ，∴△BEC ≌△FEH ，∴HE ＝EC ，∠BEC ＝∠FEH ，∴∠BEF ＝∠HEC ＝90°，∴△ECH 为等腰直角三角形．又∵CG ＝GH ，∴EG ＝CG 且EG ⊥CG ．第85题答图①第85题答图②。

2013中考数学专题训练：解不等式组1. （2012四川）设a 、b 、c 表示三种不同物体的质量，用天枰称两次，情况如图所示，则这三种物体的质量从小到大排序正确的是【 】A ．c b a <<B ．b c a <<C ．c a b <<D ．b a c << 【答案】A 。

2. （2012贵州）如图，数轴上表示某不等式组的解集，则这个不等式组可能是【 】A.x+102x 0≥⎧⎨-≥⎩B.x+102x 0≤⎧⎨-≥⎩ C. x+10x 20≤⎧⎨-≥⎩ D. x+10x 20≥⎧⎨-≥⎩【答案】A 。

3. （2012山东泰安3分）将不等式组841x x x +<-⎧⎨≤⎩ 】A ．B ．C ．D ．【答案】C 。

4. （2012山东烟台3分）不等式组的解集在数轴上表示正确的是【 】A ．B ．C ．D ．【答案】A 。

5. （2012广西钦州3分）不等式组x+202x 31>⎧⎨-≤⎩的解集在数轴上表示正确的是【 】A ．B ．C ．D ．【答案】B 。

6. （2012广东梅州7分）解不等式组：()x+302x 1+33x>⎧⎪⎨-≥⎪⎩，并判断﹣1这两个数是否为该不等式组的解．【答案】解：()x+302x 1+33x >⎧⎪⎨-≥⎪⎩①②，由①得x ＞﹣3；由②得x≤1。

∴原不等式组的解集为：﹣3＜x≤1，∵﹣3＜﹣1≤1，∴﹣1是该不等式组的解。

∵1不是该不等式组的解。

7. （2012湖南岳阳6分）解不等式组()2x+1134+x 7<⎧-≥⎪⎨⎪⎩，并将解集在数轴上表示出来．【答案】解：()2x+1134+x 7<⎧-≥⎪⎨⎪⎩ ①②，由①得2x≥2，即x≥1；由②得x ＜3。

∴不等式的解集为：1≤x ＜3。

在数轴上表示为：8. （2012湖南衡阳6分）解不等式组()()x+1>032x+56x 1⎧⎪⎨⎪≥-⎩①②，并把解集在数轴上表示出来．【答案】解：∵由①得，x ＞﹣1；由②得，x≤4，∴此不等式组的解集为：﹣1＜x≤4。