细菌觅食算法MATLAB实现

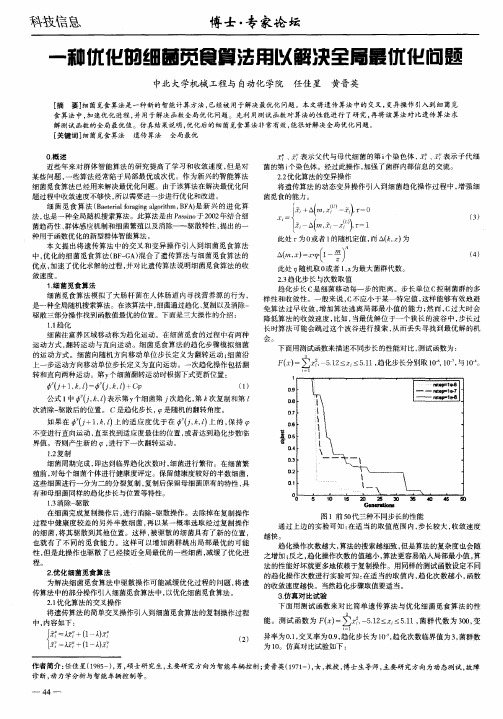
基于免疫算法的细菌觅食算法优化研究马宁;廖慧惠【摘要】细菌觅食算法BFA(Bacterial Foraging Algorithm)作为一种理论新颖、搜索机制独特的新型算法,广泛应用于各种智能优化问题.但是细菌觅食算法经常出现的速度较慢、步长一致的缺陷,提出在BFA的趋向性操作环节中调节细菌游动的步长,将步长逐步减小,以提高收敛速度.引入免疫算法中的克隆选择思想对细菌觅食算法中的复制操作进行替代;并通过实例对优化后的算法进行验证,结果表明:优化后的算法更加精确,寻优能力更强,稳定性更佳.%BFA (Bacterial Foraging Algorithm) is a new algorithm with novel theory and unique search mechanism widely used to solve intelligent optimization problems, but with low speed and uniform step length.In this paper, the step length of bacterial swimming is adjusted in the directional operation of BFA and reduced gradually to improve the convergence speed and the idea of clonal selection in immune algorithm is introduced to replace the copy operation in bacterial foraging algorithm.Case verification results show that optimized algorithm is more accurate, more powerful and more stable.【期刊名称】《菏泽学院学报》【年(卷),期】2017(039)002【总页数】7页(P19-25)【关键词】细菌觅食算法;免疫算法;优化【作者】马宁;廖慧惠【作者单位】安徽广播电视大学,安徽合肥 230022;安徽工业经济职业技术学院,安徽合肥 230051【正文语种】中文【中图分类】Q93;TP18参考自然界生物群体行为，人们相继研究出多种群体智能优化算法.其中Kenned、Eberhart两位学者在20世纪90年代中期根据鸟群捕食行为研制出PSO算法，即粒子群优化算法[1]，这一算法的应用范围极广，在各领域均发挥着重要作用[2～4]，除了各项实践问题；Passino学者依据人体肠道内大肠杆菌吞噬食物的实际过程，构建出BFA算法，即细菌觅食算法[5]，掀起了生物运算领域的研究热潮.从整体上来看，不同算法的特征各不相同，具有一定的优势和不足，BFA算法的收敛精度、搜索性能较差，但便于跳出局部极限的约束，收敛速度相对较快.很多学者开展了大量研究，一起提高BFA算法的性能，并整合了该算法和其他算法，这些整合算法主要包括分布估计算法、粒子群算法等.储颖学者[6] 就参考粒子群优化算法的信息共享机制，优化改进了细菌觅食算法的群体感应机制；DasguptaA学者[7]等将交叉、变异操作引入到原算法内，构建了混合细菌觅食算法；KimDH 学者[8]研究出GA-BFO算法；Biswas A学者[9]在细菌觅食算法的趋化算子中融入粒子群法，形成了新型算法，无需借助趋化操作；以Kim[10]为代表的学者们在BFO算法内融入变异算子及交叉算子，形成了GABFO算法；Luh学者[11]基于细菌进化的层面，构建了BEA算法(细菌进化算法)；刘小龙[12]等多位学者在繁殖算子中融入分布估计算法思路，分布估计再生的半数细菌，这些细菌都具有良好的细菌能量，对细菌自适应迁移率进行了分析，指定随机迁移了能量不良的细菌，希望改善细菌寻优性能，若在低概率下迁移能量良好的细菌，从本质上迁移即为退化解的过程，降低了寻优专区恶性，切寻优速度大大降低；Biswas学者[13]讲粒子群法引入到细菌趋化算子内，确保细菌对全局极值的感知性，借助迭代公式来更新细菌位置，弱化了趋化算子的功能性，使时间复杂性增大；Dasgupta学者[13]等将变异和交叉算子都融合到细菌进化内，丰富了种群类型，然而也存在优良个体的缺失问题.鉴于以上情况，本文通过利用免疫算法中的克隆选择思想对筛选出来的最优细菌进行繁殖变异,随着克隆细菌群落的变异以及随机交叉，进而替换细菌群落中适应度最差个体，指引算法提升搜索的精准度，并且通过调节细菌游动的步长来提高细菌觅食优化算法的收敛速度，实例证明免疫算法可以使细菌群体的搜索精度以及适应度有效提高.基于BFO算法下，模型赢编码待优化问题，对其解在搜索空间内细菌的具体状态进行定义.在处理实际问题的过程中，可以划分为以下几步：形成初始解群体、对评价函数值进行运算、借助群体彼此影响、作用机制实施迭代优化，在这个过程中应对趋化、繁殖及迁移三大算子进行循环式的执行操作，从而得到最优解.在算法模型内，对细菌实现最有觅食的行为进行模拟可以形成趋化算子，体现为在游动、翻转作用下，细菌能够游动并集中到营养较为丰富的位置，进行有目标化的运动，探索出最优路径.在细菌觅食优化算法下，细菌在不同方向上的移动单位步长即为翻转，而游动为若翻转后细菌适应值有所改善，需要继续沿此方向进行移动，实现适应值的最优化.细菌单个完整生命周期就是算法定义趋化周期，若结束生命周期，细菌会在遵循生物生存法则进行淘汰式繁殖.执行细菌觅食优化算法的过程中，应注重低等生物自身的繁殖性能及其对环境的适应能力，Passino学者将非常规的觅食策略融入到该算法的执行中，认为细菌能量就是趋化时细菌的适应值的总和，半数细菌(能量较差)在单个生命周期中死亡，且半数细菌繁殖(能量良好)变为两个子细菌，则母代细菌生物特点会被子细菌所继承.趋化算子能够使子细菌局部搜索准确性得到明显改善，细菌快速收敛性借助繁殖算子能够大大增加.如果需要解决的NP问题相对繁琐和复杂，要想不出现局部极小的状况，使算法全局寻优性能增大，就要结合算法限定，在细菌结束繁殖操作后，在搜索空间随意位置，按照特定概率对其进行迁移.由此得知，细菌局部搜索性能在BFO算法下的实现，依靠的是趋化算子能够随机搜索领域，也能够结合适应度调控方向.因为没有发挥群体周边细菌信息运用机制应用的作用，所以使算法收敛速度降低，出现局部最优的状况.完成趋化周期后，结合细菌能量，算法能够执行繁殖操作，这就能够改善寻优准确性，然而由于算法具有局部最优的缺陷，所以也会出现一系列的不熟和早熟等现象.建立在免疫系统基础上的免疫算法处于一种学习算法，涵盖于人工免疫系统研究领域.20世纪70年代，Jerne学者[14]就构建出免疫系统模型和免疫系统数学框架，之后Pereslon对上述研究成果进行完善，提出独特型网络的概率描述法[15]，并将该算法用于机器人运动路径规划领域内，并取得了明显的进步.免疫算法能够形成求解复杂系统优化问题法，与问题具体领域并没有较大的联系，在问题类型方面具有良好的鲁棒性，在不同学科中均发挥着极其重要的作用，包括控制工程领域、建筑结构设计领域及函数设计领域等.免疫算法原理相对繁琐，结合相关调查分析显示，免疫算法融合性较强[16]，能够有效融合蚁群算法、鸟群算法和主流遗传算法等，然而当前很少有研究学者分析免疫算法同细菌觅食优化算法的整合.Mori学者[17]就针对免疫算法进行了研究，认为免疫算法对抗体剑亲和度的关注程度较低，只是分析抗原、抗体剑的亲和度，其借助良好的搜索性能，能够在网络安全[18]、路径规划[19～20]等方面发挥重要作用.本研究主要针对免疫算法的克隆选择卢纶，开展其同细菌觅食算的复制融合研究，希望能够改善算法的搜索精度和整体性能.基于免疫算法的细菌觅食优化算法的实现过程为：针对细菌种群开展趋化操作.1)形成单位向量Ψ(j)，细菌进行翻转.2)对细菌的种群位置进行改善.细菌个体要结合灵敏度开展群游操作，若适应度增大到最大值，表示完成操作，则灵敏度表示成：公式内灵敏度算子是Ddlta，其数值同适应度函数变化范围有直接的联系.细菌群游式表示成：公式内趋化周期是j.3)细菌进行繁殖再生，结束趋化操作，依次按照克隆、变异、交叉和选择的顺序处理当前细菌群体.4)根据适应度加和对细菌排序，精英细菌就是待克隆群体，为Sr个细菌(适应度较强).细菌群个数的半数为精英细菌，Sr=S/2.5)克隆繁殖精英细菌，克隆群体表示为Sc，那么结合公式(3)，对适应度进行标准化处理，结合公式(4)对精英细菌的数量进行运算，得出，克隆繁殖数Sc_size，细菌个体的适应度与克隆群体的数量成正比，度量细胞抗原和抗体的亲和度递增函数表示为β.参考公式(5)进行高频变异，变异概率为δ，细菌个体适应度与变异概率越大两者呈正比关系，而且适应度越强大表示搜索空间更加广阔.结合公式(7)进行随机交叉，克隆群体内随意对差异化的细菌个体进行选择，得到k1,k2,k3,k4，免疫细胞为Si个，按照公式(8)将其融入在克隆群体内，构建出Sn，即克隆繁殖细菌群.在Sn内对适应度最强的细菌个体进行挑选，数量为Sr个，将其替换板书细菌个体(适应度不强).6)执行细菌驱散操作，在增强算法全局搜索性能的过程中，要结合驱散概率，驱散适应度不强的细菌.迁移标准细菌模式算法时，算法能够对概率ped进行确定，在解空间内对细菌个体进行随意性的迁移，如果概率ped比随机数要大，那么需要求迁移该细菌，借助该方式来提升细菌跳出局部极值的概率.鉴于算法内细菌迁移的概率一致，很可能会迁移全局最优值周边或寻优能力相对较强的细菌，就等同于细菌丢失探寻最优解的可能，迁移就会转变为退化解的过程，根本起不到改善寻优精度和加快寻优速度的效果.改进细菌的迁移操作后，就不应驱散适应度相对较强的细菌，要结合概率来对细菌执行驱散操作，这样能够消除细菌在处于全局最优化附近而被驱散现象的发生，也能够使细菌群摆脱局部最优限制的约束.7)对循环结束进行判断，若达到结束条件就应结束循环，可以将结果进行输出.结合算法基本原理，对免疫优化下细菌觅食优化算法实现流程进行归纳，结果详见图1：在DASGUPTA文章中分析BFA算法的收敛性时[13],对细菌觅食算法进行模拟菌群中每个细菌个体相互发生的影响没有进行充分的考虑.由于文中提到的融合免疫算法结合并入，因此对于融合免疫算法的收敛性需要重新进行验证.按照学者李涛的研究[14]：抗体种群为Aο，抗体空间几何I*，V(A(k))通过计算得出最优解个数B*，进行简化,可得由此可以得到此算法进行收敛直到最优解集的概率为1.如果算法迭代数量达到一定上限时，就会进行一定的收敛.在融合免疫算法中的抗体种群用A0表示,如下: 其中，Ai(k)表示细菌i在第k次操作的时候所在的位置，而Ai(k)是由Ai(k-1)经过克隆、变异而得.马尔克失链可对这一过程进行描述.为了方便表述，标记：由贝叶斯条件概率公式有：由免疫算法的特征可知：则有又因为所以故而因为所以所以综上所述，GBFA以概率1收敛.选取Sphere函数f1=(x1)、Griewank函数f2=(x2)、Rastrigrin函数f3=(x3)作为测试函数：维数皆设置为20，引用传统BFA算法和本文的融合免疫算法进行计算.其中，S=40，最大的趋势化次数Nc=20，最大的繁殖次数Nre=4，最大的迁移次数将测试曲线绘制到图2～图4.从图2～图4，可以看出：图2中，对于Sphere函数的寻优曲线，GBFA仅需要12次迭代便可以寻找出最优值，而传统BFA需要22次迭代才可以寻找出最优值，迭代次数为GBFA的2.67倍；Griewank函数具有很强的震荡性质，一般无法找到它们的最优解.从图3可以看出，传统BFA无法找到Griewank函数的最优解，但GBFA搜索到的最优解为0，说明GBFA的搜索能力远大于传统BFA.图4中，对于Rastrigrin函数的寻优曲线，GBFA仅仅需要23次迭代便可以寻找出最优值，而传统BFA需要53次迭代才可以寻找出最优值，迭代次数为GBFA的2.30倍.简而言之，GBFA的搜索能力和搜索速度远大于传统BFA.GBFA和传统BFA收敛精度的比较见表1.通过表1，对于Sphere函数f1(x1)、Griewank函数f2(x2)、Rastrigrin函数f3=(x3)，融合免疫算法的精度远大于传统BFA，寻优能力更强.并且，融合免疫算法的方差均小于传统BFA的方差，说明融合免疫算法的稳定性更好.本文针对BFA算法的三个操作环节(复制操作环节、趋向性操作环节和迁移操作环节)，免疫算法克隆选择思想的相关思想，提出BFA的一种融合免疫算法.并利用Sphere函数f1(x1)、Griewank函数f2(x2)、Rastrigrin函数f3(x3)作为实例进行验证，发现融合免疫算法的搜索能力和搜索速度远大于传统BFA，寻优能力更强、稳定性更好.【相关文献】[1]黄少荣．粒子群优化算法综述[J]．计算机工程与设计，2009(8):1977-1980.[2]付志军，冯丽，杜伟宁，等．离散粒子群优化算法在流水作业调度问题中的应用[J]．吉林大学学报: 理学版，2014，52(3):561-564.[3]任贝，韩飞，吴坚．基于遗传算法的摄像机标定[J].吉林大学学报: 信息科学版,2013(4) : 432-436.[4]张杭悦，陈谋．基于混合优化鱼群算法的近空间飞行器控制分配[J]．吉林大学学报: 信息科学版，2014(4):369-376． [5]周雅兰．细菌觅食优化算法的研究与应用[J].计算机工程与应用,2010,46(20):16-21． [6]储颖，糜华，纪震，等.基于粒子群优化的快速细菌群游算法[J]．数据采集与处理，2010，25(4) : 442-448． [7]Dasgupta A, Dasgupta S, Das S, et al. A synergyof differential evolution andbacterial foraging optimization.for global optimization[J]. Neural Network Word,2007,17(6): 607-626.[8]Kim D H, Abraham A, Cho J H. A hybrid genetic algorithm and bacterial foraging approach[J]. Information Sciences, 2007, 177(18): 3918-3937.[9]Biswas A, Dasgupta S, Das S, et al. Synergy of PSO and bacterial foraging op-timization:A comparative study on numerical benchmarks[C]. Proc of the 2nd IntSymposium on Hybrid Artificial Intelligent Systems. Salamanca, 2007:255-263.[10]NAYAGAMA V L G，MURALIKRISHNAN S，SIVARAMAN G．Multi-criteria decision-making method based on interval-valued intuitionistic fuzzy sets[J]．Expert Systems with Applications，2011，38(3) : 1464-1467． [11]NAYAGAMAVLG，SIVARAMAN G．Ranking of interval valuedintuitionistic fuzzy sets[J]．Applied Soft Computing，2011，11(4) :3368-3372.[12]刘小龙，李荣钧，杨萍．基于高斯分布估计的细菌觅食优化算法[J]．控制与决策，2011，26(8) : 1233-1238.[13]BISWASA，DASGUPTAS，DASS，etal．Synergy of PSO and bacterial foragingoptimization—A comparative study on numericalbenchmarks[EB /OL]．[2010-05-10]．http: //www．softcomputing．net/hais072．pdf.[14]Jerne.N.K. Towards a Network Theory of the Immune System. Annual Immunology, 1974,125C:373-389.[15]Perelson.A.S. Immune Network Theory. Immunological Review,1989,10:5-36.[16]莫宏伟．人工免疫系统原理与应用[M]．哈尔滨: 哈尔滨工业大学出版社，2002.[17]MORI K，TSUKIYAMA M，FUKUDA T．Immune Algorithm with Searching Diversity and Its Application to Resource Allocation Problem[J]．Transactions-Institute of Electrical Engineers of Japan，1993，113C(10) : 872-878.[18]刘丽峰，张树清，李新红．人工免疫算法路径规划在林火救援中的应用[J]．吉林大学学报: 信息科学版，2012，30(4):433-440.[19]江超，王海燕，陈磊，等．基于生物免疫原理的新型无线传感器网络安全算法[J]．吉林大学学报: 理学版，2013，50(6):1204-1208.[20]胡亮，王程明，赵阔，等．基于人工免疫模型的入侵检测系统中检测器生成算法的分析与改进[J]．吉林大学学报:理学版，2010，48(1) : 67-72．。

细菌觅食机制粒子群优化算法程军;吴燕子【摘要】针对基本粒子群优化算法易陷入局部极值的缺陷，提出了一种细菌觅食机制粒子群优化算法。

其基本思想是在粒子群优化算法中引入细菌觅食行为机制，提高PSO算法跳出局部极值的能力，借以改善PSO算法的寻优性能。

采用标准测试函数的实验结果表明，该算法在收敛速度和求解精度方面均有显著改进。

%A novel particle swarm optimization algorithm based on bacterial foraging mechanism ( PSOBF ) is proposed for conventional particle swarm optimization algorithms ( PSO) often trapped in local optima.The basic idea is to introduce the bacterial foraging mechanism into particle swarm optimization algorithm to improve the ability of PSO algorithm.The experimental results of six benchmark functions demonstrate the efficacy of the present algorithm.【期刊名称】《广州航海高等专科学校学报》【年(卷),期】2015(000)002【总页数】4页(P36-39)【关键词】粒子群优化算法;细菌觅食;机制【作者】程军;吴燕子【作者单位】广州航海学院港口与航运管理系，广东广州510725; 华南理工大学工商管理学院，广东广州510640;广州航海学院港口与航运管理系，广东广州510725【正文语种】中文【中图分类】TP18由Kennedy和Eberhart[1]在1995年提出的粒子群优化算法(Particle Swarm Optimization, PSO)，对参数搜索空间没有如连续、可导及单峰等苛刻的要求，因此在众多经济管理、工程技术等实际问题中获得了成功的应用[2]．针对PSO容易陷入早熟或不熟的缺陷，改进的途径主要表现在粒子群初始化、拓扑结构设计、参数选择、与其他智能算法混合等方面[3]．近年来，将生物觅食机制融入PSO算法为改进PSO算法的性能提供了新途径．王联国等[4]将人工鱼群算法中的改进觅食算子引入基本PSO算法，提出了一种具有觅食算子的PSO算法，改善算法的全局优化能力及提高算法的收敛速度和计算精度；刘伟等[5]提出基于细菌觅食机制改进粒子群算法，采用PSO 算法完成整个空间的全局搜索，通过细菌觅食算法(BFOA) 中的趋向性运动算子完成局部搜索的功能．本文在现有研究的基础上根据细菌觅食行为规律，提出一种基于细菌觅食机制的粒子群优化算法PSOBF(particle swarm optimization based on bacterial foraging mechanism)，我们将细菌觅食机制嵌入PSO，构造PSOBF算法模型，其主要思想是在粒子群优化算法中引入细菌觅食行为，提高PSO算法跳出局部极值的能力，借以改善PSO算法的寻优性能．标准测试函数的实验结果表明该算法收敛速度快，求解精度高．微生物领域针对大肠杆菌(E. Coli)的研究发现，细胞膜、细胞壁、细胞质和细胞核是大肠杆菌的基本组成部分，在大肠杆菌的周围分布着纤毛和鞭毛，纤毛是一种突起状的细胞，能通过运动为细菌传递信息，鞭毛是菌体上细长而且弯曲的丝状物，作为细菌的运动器官，其功能是帮助细胞进行移动[6]．大肠杆菌在适宜的环境中生存和进化，其繁殖过程是在自身长到一定长度后，在身体的中部进行裂变一分为二，形成两段构成新的个体．大肠杆菌在觅食的过程中表现出一定的记忆能力，实现对所经过的环境状态的记忆，帮助其在觅食过程中往食物源方向靠近，并且避开有毒物质．在大肠杆菌趋向食物方向移动的过程中，会对每次经过的状态进行评价，提供相应的信息帮助其采取有效的措施进而改变下一步的状态[7]．大肠杆菌的生存环境会因为各种因素的影响而改变，这些因素包括来自细菌自身的活动，如大肠杆菌消化食物导致其周围环境的改变，也包括来自外界环境的变化，如细菌生存环境温度的急剧上升可以导致该环境下细菌的死亡，水的冲刷作用将细菌从一个环境迁移到另外一个新的环境．进一步的研究发现，在细菌群落中存在一种能进行信息交流的群体感应机制，细菌通过自身产生的小信号分子进行群体通信，我们将这种物质称为“自我诱导物”．细菌根据自我诱导物数量的多少来判断细菌邻域的群体密度，采取相应的措施来调整其生理行为[8]．细菌通过群体感应机制来判断邻域内的其他细菌数量，当细菌所处的环境中自我诱导物浓度较低时，细菌无法感应到其他细菌的存在；当一定数量的细菌聚集在某个区域，会导致自我诱导物浓度增加并达到一定的阈值，细菌会被该区域所吸引，这时的自我诱导物就成为一种吸引剂；当细菌数量在该区域继续增加时，自我诱导物质的浓度会进一步增强，当自我诱导物浓度增加到超过了某个阈值时，细菌会释放出另外一种用来阻止细菌过度聚集的自我诱导物，我们称之为排斥剂．细菌在觅食过程中，通过翻转(tumble)和游动(run)向营养丰富的区域靠近，而群体内存在细菌相互影响和作用的机制，借助趋化(chemotaxis)、繁殖(reproduction)和迁移(elimination-dispersal)等功能，实现最优化的觅食[9]．在细菌的生命周期中，按照优胜劣汰、适者生存的自然法则进行繁殖，细菌作为低等生物，具有很强的环境适应能力和繁殖能力．Passino采用非常规的觅食策略构造了细菌觅食算法，将细菌能量定义为趋化过程中细菌适应度值的累加和，在生命周期内根据细菌能量的优劣来更新种群，具体做法是将能量较好的一半细菌进行繁殖一分为二，新的细菌继承了原始细菌的位置、移动步长和能量等生物特性，而将能量较差的一半细菌淘汰[10]．PSO在拥有原理简单、容易操作等优点的同时，还存在一些无法克服的缺陷，比如进化过程中群体多样性的减少、缺乏有效的机制跳出局部极值导致算法“早熟”．鉴于细菌觅食过程中表现出的优良特性，我们将细菌觅食机制嵌入PSO，构造PSOBF算法模型，其主要思想是在粒子群优化算法中引入细菌觅食行为，提高PSO算法跳出局部极值的能力，借以改善PSO算法的寻优性能．PSOBF算法的主要步骤如下：步骤1：在初始化范围内对粒子群的位置和速度进行非对称初始化．步骤2：计算所有粒子的适应度值，将粒子的当前位置设置为个体历史最好位置，将所有粒子适应度值最优的位置作为全局最优．步骤3：判断迭代次数是否小于设定值，是则进入下一步，否则转入步骤8．步骤4：采用更新公式更新粒子的速度和位置．步骤5：重新计算粒子的适应度值，将结果与个体的历史最优值比较，如果更优，则将该粒子现在的位置作为新的个体最优值点．步骤6：将粒子的个体历史最优与群体最优值进行比较，若更优，则将其作为当前全局最优位置．步骤7：计算能量值，当其满足条件时发生繁殖，能量值较好的个体繁殖出个体，取代能量值较差的个体，转入步骤4．步骤8：输出结果．3.1 测试函数本文选取智能优化中6个常用的测试函数进行分析，详细描述见表1．其中,f1，f2是单峰函数,f3-f6属于多峰函数. 在表1中给出每个函数的表达式、搜索范围以及初始化范围．3.2 实验参数设置依然选择前述的f1～f6共6个标准测试函数进行仿真实验，每个标准测试函数的初始化参数设置见表1．将测试函数的维数设置为D=30，种群的粒子数量设置为n=80，采用非对称初始化将初始化的范围确定在搜索空间的一部分，对SPSO，PSOPB，PSOBF的速度上下限设置为Vmax=Ud，Vmin=Ld，参数设置依据文献[11]选取，ω=0.729，c1=c2=2.05，仿真实验的测试平台采用Windows 7系统，仿真软件matlab 7.0，实验设置的最大迭代次数为6 000次，每个实验独立运行50次．3.3 实验结果与分析将3种粒子群算法对6个测试函数分别独立运行50次，最大迭代次数为6 000，得到的实验结果如表2所示．表2中给出了各函数对每种算法独立测试50次结果的最佳值、最差值、平均值、标准差、计算所耗费时间5个指标衡量．从表2和计算过程可以看出：对于单峰函数f1，PSOBF比SPSO和PSOPB具有更快的收敛速度和更高的搜索精度，计算时间也比较节省；对于单峰函数f2，PSOBF和PSOPB在搜索后期的收敛速度要优于SPSO，PSOBF和PSOPB在寻优性能方面各有优劣，但总体相差不大；对于多峰函数f3，在搜索过程的早期PSOBF的收敛速度优于PSOPB，但在搜索后期PSOBF的收敛速度有所减缓；对于多峰函数f4，PSOBF的整体寻优性能略优于PSOPB；对于多峰函数f5，PSOBF的收敛速度优于SPSO，但比PSOPB的寻优性能略微逊色；对于多峰函数f6，PSOBF的收敛速度要明显优于PSOPB和SPSO．本文构建了一种基于细菌觅食机制的改进粒子群算法(PSOBF)．该算法将细菌觅食机制嵌入PSO进而构造PSOBF算法模型，在粒子群优化算法中引入细菌觅食行为，利用细菌觅食过程中表现出的优良特性来提高PSO算法跳出局部极值的能力，以实现改善PSO算法的寻优性能．实验结果表明该方法在收敛性方面有显著改进．【相关文献】[1] KENNEDY J, EBERHART R C. Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks IV. Piscataway:IEEE, 1995: 1942-1948.[2] 谢晓锋, 张文俊, 杨之廉. 微粒群算法综述[J]. 控制与决策, 2003, 18(2): 129-133.[3] ANGELINE P J. Using selection to improve particle swarm optimization[C]//Proc of IEEE World Congress on Computational Intelligence. Anchorage:IEEE, 1998: 84-89.[4] 王联国, 洪毅, 赵付青. 基于觅食算子的粒子群优化算法[J]. 计算机应用与软件, 2009, 26(11): 112-115.[5] 刘伟, 陈舒, 王圣慧, 等. 基于细菌觅食机制改进粒子群算法的研究[J]. 系统仿真技术, 2012, 8(1): 23-26.[6] ALBERTS B, BRAY D, LEWIS J, et al. Watson. Molecular Biology of the Cell [M]. New York:Garland Publishing, 1989: 902-903.[7] BERG H. Motile behavior of bacteria [J]. Phys. Today，Jan, 2000(1): 24-29.[8] 李任峰，何启盖，周锐，等. 细菌鞭毛研究概况及进展[J]. 微生物学通报，2005，32(6)：124-127.[9] 刘小龙，李荣钧，杨萍. 基于高斯分布估计的细菌觅食优化算法[J]. 控制与决策，2011，26(8)：1233-1238.[10] PASSINO K M. Biomimicry of Bacterial Foraging for Distributed Optimization and Control [J]. IEEE Control Systems, 2002, 22(3): 52-67.[11] 常先英. 粒子群优化算法的改进及应用[D]. 广州：华南理工大学，2009.。

基于自适应的细菌觅食算法童雅林【期刊名称】《价值工程》【年(卷),期】2015(34)11【摘要】针对细菌觅食（BFO）算法存在容易陷入局部最优、求解精度不高、收敛速度慢等问题，提出一种新的基于自适应的算法。

算法主要对趋化和复制两个关键步骤进行改进，自适应地调整游动步长，并在复制操作中引入轮盘赌选择机制，使算法快速收敛到全局最优解以改善细菌觅食算法的性能。

实验结果表明，提出的算法不仅收敛速度快，且求解精度高。

%There are some problems in bacteria foraging optimization (BFO) algorithm, it is easy to fall in local optimum and it has relatively low accuracy and slow convergence speed. A new algorithm based on self-adaptative method was proposed to solve these problems. This paper mainly focused on improving two key steps of BFO, chemotaxis and reproduction. The swimming stepsize was adaptively adjusted to make the algorithm rapidly converge to the global optimum, and the roulette wheel selection was introduced into the reproduction step. Experimental results show that the proposed algorithm has high convergence speed and accuracy.【总页数】4页(P194-197)【作者】童雅林【作者单位】合肥工业大学，合肥230009【正文语种】中文【中图分类】TP391.4【相关文献】1.基于正态云模型的自适应细菌觅食优化算法 [J], 杜文军;孙斌2.基于细菌觅食算法的自适应NURBS曲线插补 [J], 谷岩;周岩;林洁琼;曹东旭;刘阳;孙彦东3.基于自适应细菌觅食算法的集装箱装载 [J], 范霁月;高尚;张晓庆4.基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法 [J], 商立群;朱伟伟5.基于Log-Linear模型的Gauss-Cauchy自适应细菌觅食算法 [J], 王圣;闫仁武因版权原因，仅展示原文概要，查看原文内容请购买。

信 息 技 术31科技资讯 SCIENCE & TECHNOLOGY INFORMATIONDOI：10.16661/ki.1672-3791.2018.02.031基于细菌觅食算法的排班智能优化张永棠（广东东软学院 广东佛山 528225）摘 要:智能排班问题是极为复杂的组合优化问题。

它包含了劳动法约束、员工层级、不同层级的工资策略、不同班次的工资策略、资源需求等复杂因素。

我们以南昌某医院护士排班智能优化为例，选取了基于细菌觅食优化的算法来为此类问题进行优化求解。

为了提高算法的搜索能力，将信息交流机制加入到细菌在趋化过程中的翻转方向选择上，研究了基于四种静态拓扑结构和一种动态拓扑结构的邻域结构下的细菌觅食优化算法。

关键词:智能优化 群体智能 调度 细菌觅食算法中图分类号:TP18 文献标识码:A 文章编号:1672-3791(2018)01(b)-0031-02随着人们对于健康保健意识的日益增强，患者及家属对护理服务的需求不断提高。

如何有效分配护理资源管理、为病人提供高品质的服务并有效控制预算是当今当前医院护理管理所面临的重大课题。

但是在实际中，劳动法规约束、个人能力的差别、应急性、工作时间不稳定等因素导致实现较好的护理管理困难重重。

智能排班问题（Intelligent Rostering Problem，简称I R P）是指在给定的排班时间段内为特定的一组员工安排班次，并使该排班方案满足各种硬性约束条件，同时尽量满足各种软性约束条件，并在此基础上优化相关性能指标。

因此，智能排班问题是一个极为复杂的组合优化问题，也是现代人力资源管理亟待解决的一大难题。

1 排班问题本文研究以南昌某医院的护士排班问题为例。

在给定的一个排班周期内对于一定数量的包括不同等级的护士进行排班安排。

需要考虑的条件有：满足国家劳动法规定、医院一系列约束条件，满足医院工作需求，护士合理要求。

本文研究的护士排班问题主要有以下特点：(1)护士每天的工作分为三种班次，分别为早班(0点～8点）、白班（8点～16点）、晚班（16点～24点）。

nsga-ⅲ算法matlab代码及注释一、NSGA-Ⅲ算法简介NSGA-III算法是多目标优化领域的一种经典算法，它是基于非支配排序的遗传算法。

该算法通过模拟自然选择的过程，不断改进种裙中的个体，以寻找Pareto前沿上的最优解。

NSGA-III算法在解决多目标优化问题方面表现出色，广泛应用于工程、经济和管理等领域。

二、代码实现下面是NSGA-III算法的Matlab代码示例，包含了代码的注释和解释。

```matlab初始化参数pop_size = 100; 种裙大小max_gen = 100; 最大迭代次数p_cross = 0.8; 交叉概率p_mut = 0.1; 变异概率n_obj = 2; 目标函数数量初始化种裙pop = initialization(pop_size);进化过程for gen = 1:max_gen非支配排序和拥挤度距离计算[fronts, cd] = non_dominated_sort(pop);种裙选择offspring = selection(pop, fronts, cd, pop_size);交叉和变异offspring = crossover(offspring, p_cross);offspring = mutation(offspring, p_mut);合并父代和子代种裙pop = merge_pop(pop, offspring, pop_size);end结果分析pareto_front = get_pareto_front(pop);plot_pareto_front(pareto_front);```三、代码解释1. 初始化参数：设置种裙大小、最大迭代次数、交叉概率、变异概率和目标函数数量等参数。

2. 初始化种裙：调用初始化函数，生成初始的种裙个体。

3. 进化过程：在每一代中，进行非支配排序和拥挤度距离计算，然后进行种裙选择、交叉和变异操作，最后合并父代和子代种裙。

蝙蝠算法matlab程序蝙蝠算法（Bat Algorithm）是一种启发式算法，用于解决优化问题。

它模拟了蝙蝠捕食时的行为，通过调整蝙蝠位置和频率来寻找最优解。

在Matlab中，可以实现蝙蝠算法的程序来解决各种优化问题。

以下是一个简单的蝙蝠算法的Matlab程序示例：matlab.function [best, fmin]=bat_algorithm()。

% 初始化参数。

N=40; % 蝙蝠个数。

n=2; % 优化问题的维度。

A=0.5; % 蝙蝠的响度。

r=0.5; % 蝙蝠的脉冲发射率。

Qmin=0; % 最小频率。

Qmax=2; % 最大频率。

% 随机生成初始种群。

if isvector(Lb)。

Lb=Lb'; Ub=Ub';end.% 随机生成初始种群。

Q=zeros(N,1); v=zeros(N,n); Sol=zeros(N,n);for i=1:N.Sol(i,:)=Lb+(Ub-Lb).rand(1,n); end.% 初始化适应度值。

fitness=zeros(N,1);% 最优解。

best=zeros(1,n);fmin=inf;% 开始迭代。

for t=1:Max_iteration.% 随机选择频率。

for i=1:N.Q(i)=Qmin+(Qmin-Qmax)rand;v(i,:)=v(i,:)+(Sol(i,:)-best)Q(i); S=Sol(i,:)+v(i,:);% 边界处理。

for j=1:n.if S(j)<Lb(j)。

S(j)=Lb(j);elseif S(j)>Ub(j)。

S(j)=Ub(j);end.end.if rand<A.S=best+0.001randn(1,n);end.% 评估新解。

Fnew=benchmark_func(S);% 判断是否更新最优解。

if (Fnew<=fitness(i)) && (rand<r)。

bfo算法matlab代码BFO算法是一种基于生物学的优化算法，它模拟了生物体内的化学反应过程，通过不断的迭代来寻找最优解。

BFO算法的优点在于可以处理多维度的优化问题，并且具有较好的全局搜索能力。

下面将介绍BFO算法的MATLAB代码实现。

BFO算法的MATLAB代码实现：1. 初始化参数首先，我们需要初始化一些参数，包括化学反应的速率常数、扩散速率常数、步长、精度等。

这些参数的设置会影响算法的收敛速度和精度。

2. 随机生成初始解接下来，我们需要随机生成一些初始解，这些解将作为化学反应的初始物质。

初始解的数量可以根据问题的复杂度来确定。

3. 计算适应度函数对于每个初始解，我们需要计算它的适应度函数值。

适应度函数是问题的目标函数，它的值越小表示解越优。

4. 执行化学反应根据化学反应的速率常数和扩散速率常数，我们可以计算出每个初始解的化学反应速率和扩散速率。

然后，根据这些速率，我们可以计算出每个初始解的浓度变化量。

最后，根据浓度变化量和步长，我们可以更新每个初始解的位置。

5. 执行扩散过程在化学反应之后，我们需要执行扩散过程，以便更好地探索解空间。

扩散过程是通过随机扰动每个初始解的位置来实现的。

扰动的大小可以根据问题的复杂度来确定。

6. 重复执行化学反应和扩散过程通过不断地执行化学反应和扩散过程，我们可以逐步优化解的质量。

当达到一定的迭代次数或者解的质量满足一定的要求时，算法停止。

7. 输出最优解最后，我们输出最优解及其适应度函数值，以便进行后续的分析和应用。

总结：BFO算法是一种基于生物学的优化算法，它模拟了生物体内的化学反应过程，通过不断的迭代来寻找最优解。

BFO算法的MATLAB代码实现比较简单，只需要初始化参数、随机生成初始解、计算适应度函数、执行化学反应和扩散过程等几个步骤。

通过不断地执行化学反应和扩散过程，我们可以逐步优化解的质量，最终得到最优解及其适应度函数值。

免疫算法的matlab代码摘要：1.免疫算法简介2.Matlab代码实现免疫算法的基本步骤3.免疫算法在实际问题中的应用4.代码运行结果与分析正文：免疫算法（Immune Algorithm）是一种模拟自然界免疫机制的优化算法，它具有较强的全局搜索能力，适用于解决复杂优化问题。

本文将介绍如何使用Matlab编写免疫算法的代码，并对其进行简要分析。

1.免疫算法简介免疫算法基于生物免疫系统的原理，通过模拟免疫细胞的作用机制进行问题求解。

算法主要包括两个部分：抗原和抗体。

抗原表示问题空间中的目标函数，抗体则表示问题的解。

算法通过不断更新抗体，寻找最优解。

2.Matlab代码实现免疫算法的基本步骤以下是免疫算法在Matlab中的基本实现步骤：（1）初始化抗体群：随机生成一定数量的抗体，作为初始种群。

（2）计算适应度：根据问题特点，计算每个抗体对应的适应度值。

（3）选择操作：根据适应度值，选择一部分优秀抗体进行繁殖。

（4）变异操作：对选中的抗体进行变异，以增加算法的多样性。

（5）免疫操作：根据抗体之间的相似度，进行免疫更新。

（6）判断收敛条件：当满足收敛条件时，停止迭代，输出当前最优解。

3.免疫算法在实际问题中的应用免疫算法在许多实际问题中表现出良好的性能，例如物流配送中心选址问题、机器人路径规划等。

以下是一个免疫算法在物流配送中心选址问题中的应用实例：问题描述：假设有一个物流网络，包含多个需求点和仓库。

目标是选择一个最佳仓库作为配送中心，使得整个物流网络的运输成本最低。

解决方案：使用免疫算法求解配送中心选址问题。

首先，将仓库位置作为抗体，计算每个抗体对应的适应度值（即物流成本）。

然后，通过迭代更新抗体，直到满足收敛条件。

最后，输出最优仓库位置作为配送中心。

4.代码运行结果与分析运行免疫算法代码后，可以得到物流配送中心的最优选址。

通过对比不同算法的结果，可以发现免疫算法在求解此类问题时具有较快的收敛速度和较高的全局搜索能力。