【小站教育】SAT数学难题汇总及答案.docx

SAT Subject Test Practice - Results Summary Mathematics Level 21Your answer Omitted!What is the distance in space between the points with coordinates and ?(A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is D.The distance between the points with coordinates and is given by the distance formula: .Therefore, the distance between the points with coordinates and is:,which simplifies to .2Your answer Omitted!If , what value does approach as gets infinitely larger?(A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is E.One way to determine the value that approaches as gets infinitely larger is to rewrite the definition of the function to use only negative powers of and then reason about the behavior of negative powers of as gets infinitely larger. Since the question is only concerned with what happens to as gets infinitely larger, one can assume that is positive. For , theexpression is equivalent to the expression . As gets infinitely larger, the expression approaches the value , so as gets infinitely larger, the expression approaches the value . Thus, as gets infinitely larger, approaches .Alternatively, one can use a graphing calculator to estimate the height of the horizontal asymptote for the function . Graph the function on an interval with “large”, say, from to .By examining the graph, the all seem very close to . Graph the function again, from, say, to .The vary even less from . In fact, to the scale of the coordinate plane shown, the graph of the function is nearly indistinguishable from the asymptotic line . This suggests that as gets infinitely larger, approaches , that is, .Note: The algebraic method is preferable, as it provides a proof that guarantees that the value approaches is . Although the graphical method worked in this case, it does not provide a complete justification; for example, the graphical method does not ensure that the graph resembles a horizontal line for “very large”such as .3Your answer Omitted!If is a factor of , then(A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is A.By the Factor Theorem, is a factor of only when is a root ofthat is, , which simplifies to . Therefore, .Alternatively, one can perform the division of by and then find a value for so that the remainder of the division is .Since the remainder is , the value of must satisfy . Therefore, .4Your answer Omitted!Alison deposits into a new savings account that earns percent interest compounded annually. If Alison makes no additional deposits or withdrawals, how many years will it take for the amount in the account to double?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumAfter year, the amount in the account is equal to . After years, the amount isequal to , and so on. After years, the amount is equal to . You needto find the value of for which . There are several ways to solve this equation. You can use logarithms to solve the equation as follows.Since , it will take more than years for the amount in the account to double. Thus, you need to round up to .Another way to find is to use your graphing calculator to graph and . From the answer choices, you know you need to set the viewing window with values from to about and values extending just beyond . The of the point of intersection is approximately . Thus you need to round up to .5Your answer Omitted!In the figure above, when is subtracted from , what is the length of the resultant vector?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe resultant of can be determined by . The length of the resultant is:6Your answer Omitted!In the -plane, what is the area of a triangle whose vertices are , , and ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt is helpful to draw a sketch of the triangle:The length of the base of the triangle is and the height of the triangle is . Therefore, the area of the triangle is . The correct answer is B.7Your answer Omitted!A right circular cylinder has radius and height . If and are two points on its surface, what is the maximum possible straight-line distance between and ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe maximum possible distance occurs when and are on the circumference of opposite bases: You can use the Pythagorean Theorem:The correct answer is (B).8Your answer Omitted!Note: Figure not drawn to scale.In the figure above, and the measure of is . What is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThere are several ways to solve this problem. One way is to use the law of sines. Since ,the measure of is and the measure of is . Thus, and . (Make sure your calculator is in degree mode.)You can also use the law of cosines:Since is isosceles, you can draw the altitude to the triangle.9Your answer Omitted!The function is defined by for .What is the difference between the maximum and minimum values of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt is necessary to use your graphing calculator for this question. First graph the function. It is helpful to resize the viewing window so the -values go fromto . On this interval the maximum value of is and the minimum value of is. The difference between these two values is , which rounds to .10Your answer Omitted!Suppose the graph of is translated units left and unit up. If the resulting graph represents , what is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt may be helpful to draw a graph of and .The equation for is . Therefore,. The correct answer is B.11Your answer Omitted!A sequence is recursively defined by , for . If and , what is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe values for and are given. is equal to . is equal to. is equal to . is equal to.If your graphing calculator has a sequence mode, you can define the sequence recursively and findthe value of . Let , since the first term is . Define . Let , since we have to define the first two terms and . Then examining a graph or table, you can find .12Your answer Omitted!The diameter and height of a right circular cylinder are equal. If the volume of the cylinder is , what is the height of the cylinder?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is A.To determine the height of the cylinder, first express the diameter of the cylinder in terms of theheight, and then express the height in terms of the volume of the cylinder.The volume of a right circular cylinder is given by , where is the radius of the circular base of the cylinder and is the height of the cylinder. Since the diameter and height are equal, . Thus . Substitute the expression for in the volume formula to eliminate :. Solving for gives . Since the volume of the cylinder is , theheight of the cylinder is .13Your answer Omitted!If ,then(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is E.One way to determine the value of is to apply the sine of difference of two angles identity: . Since and , the identity gives . Therefore, .Another way to determine the value of is to apply the supplementary angle trigonometric identity for the sine: . Therefore, .14Your answer Omitted!A line has parametric equations and , where is the parameter. The slope of the line is(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is B.One way to determine the slope of the line is to compute two points on the line and then use the slope formula. For example, letting gives the point on the line, and letting gives the point on the line. Therefore, the slope of the line is equal to .Alternatively, one can express in terms of . Since and , it follows that . Therefore, the slope of the line is .15Your answer Omitted!What is the range of the function defined by ?(A) All real numbers(B) All real numbers except(C) All real numbers except(D) All real numbers except(E) All real numbers between andExplanationDifficulty: MediumThe correct answer is D.The range of the function defined by is the set of such thatfor some .One way to determine the range of the function defined by is to solve the equation for and then determine which correspond to at least one . To solve for , first subtract from both sides to get and then take the reciprocal of both sides to get . The equation shows that for anyother than , there is an such that , and that there is no such for . Therefore, the range of the function defined by is all real numbers except .Alternatively, one can reason about the possible values of the term . The expression can take on any value except , so the expression can take on any value except . Therefore, the range of the function defined by is all real numbers except .16Your answer Omitted!The table above shows the number of digital cameras that were sold during a three-day sale. The prices of models , , and were , , and , respectively. Which of the following matrix representations gives the total income, in dollars, received from the sale of the cameras for each of the three days?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is C.A correct matrix representation must have exactly three entries, each of which represents the total income, in dollars, for one of the three days. The total income for Day is given by the arithmetic expression , which is the single entry of the matrix product; in the same way, the total income for Day is given by, the single entry of ; and the total income for Day is given by , the single entry of. Therefore, the matrix representationgives the total income, in dollars, received from the sale of the cameras for each of the three days. Although it is not necessary to compute the matrix product in order to answer the question correctly, equals .17Your answer Omitted!The right circular cone above is sliced horizontally forming two pieces, each of which has the sameheight. What is the ratio of the volume of the smaller piece to the volume of the larger piece?(A)(B)(C)(D)(E)ExplanationDifficulty: HardIt is helpful to label the figure.The top piece is a cone whose height is one-half the height of the original cone . Using the properties of similar right triangles, you should realize the radii of these two cones must be in the same ratio. So if the top cone has radius , the original cone has radius .The volume of the top piece is equal to . The volume of the bottom piece is equal to the volume of the original cone minus the volume of the top piece.The ratio of the volume of the smaller piece to the volume of the larger piece is .18Your answer Omitted!In the figure above, is a regular pentagon with side of length . What is the -coordinate of ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe sum of the measures of the interior angles of a regular pentagon is equal to . Each interior angle has a measure of . Using supplementary angles, has a measure of . You can use right triangle trigonometry to find the -coordinate of point .Since , is about . Since the length of each side of the pentagon is , the -coordinate of point is . Putting the information together tells us that the -coordinate of point is . The correct answer is (B).19Your answer Omitted!For a class test, the mean score was , the median score was , and the standard deviation of the scores was . The teacher decided to add points to each score due to a grading error. Which of the following statements must be true for the new scores?I. The new mean score is .II. The new median score is .III. The new standard deviation of the scores is .(A) None(B) only(C) only(D) and only(E) , , andExplanationDifficulty: HardFor this type of question you need to evaluate each statement separately. Statement is true. If you add to each number in a data set, the mean will also increase by . Statement is also true. The relative position of each score will remain the same. Thus, the new median score will be equal to more than the old median score. Statement is false. Since each new score is more than the old score, the spread of the scores and the position of the scores relative to the mean remain the same. Thus, the standard deviation of the new scores is the same as the standard deviation of the old scores.20Your answer Omitted!A game has two spinners. For the first spinner, the probability of landing on blue is . Independently, for the second spinner, the probability of landing on blue is What is the probability that the first spinner lands on blue and the second spinner does not land on blue?(A)(B)(C)(D)(E)ExplanationDifficulty: HardSince the two events are independent, the probability that the first spinner lands on blue and the second spinner does not land on blue is the product of the two probabilities. The first probability is given. Since the probability that the second spinner lands on blue is the probability that thesecond spinner does not land on blue is Therefore, . The correct answer is (E).21Your answer Omitted!In January the world’s population was billion. Assuming a growth rate of percent per year, the world’s population, in billions, for years after can be modeled by theequation . According to the model, the population growth from January to January was(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is C.According to the model, the world’s population in January was and in January was . Therefore, according to the model, the population growth from January to January , in billions, was , or equivalently,.22Your answer Omitted!What is the measure of one of the larger angles of a parallelogram in the that has vertices with coordinates , , and ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is C.First, note that the angle of the parallelogram with vertex is one of the two larger angles of the parallelogram: Looking at the graph of the parallelogram in the makes this apparent. Alternatively, the sides of the angle of the parallelogram with vertex are a horizontal line segment with endpoints and and a line segment of positive slope with endpoints and that intersects the horizontal line segment at its left endpoint , so the angle must measure more than Since the sum of the measures of the four angles of aparallelogram equals , the angle with vertex must be one of the larger angles.One way to determine the measure of the angle of the parallelogram with vertex is to apply the Law of Cosines to the triangle with vertices , , and . The length of the two sides of the angle with vertex are and; the length of the side opposite the angle is . Let represent the angle with vertex and apply the Law of Cosines: , so. Therefore, the measure of one of the larger angles of the parallelogram is .Another way to determine the measure of the angle of the parallelogram with vertex is to consider the triangle , , and . The measure of the angle of this triangle with vertex is less than the measure of the angle of the parallelogram with vertex . The angle of the triangle has opposite side of length and adjacent side of length , so the measure of this angle is . Therefore, the measure of the angle of the parallelogram withvertex is .Yet another way to determine the measure of the angle of the parallelogram with vertex is to use trigonometric relationships to find the measure of one of the smaller angles, and then use the fact that each pair of a larger and smaller angle is a pair of supplementary angles. Consider the angle of the parallelogram with vertex ; this angle coincides with the angle at vertex of the right triangle with vertices at , , and , with opposite side of lengthand adjacent side of length , so the measure of this angle is . This angle, together with the angle of the parallelogram with vertex , form a pair of interior angles on the same side of a transversal that intersects parallel lines, so the sum of the measures of the pair of angles equals . Therefore, the measure of the angle of the parallelogram with vertex is.23Your answer Omitted!For some real number , the first three terms of an arithmetic sequence are, and . What is the numerical value of the fourth term?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is E.To determine the numerical value of the fourth term, first determine the value of and then apply the common difference.Since , and are the first three terms of an arithmetic sequence, it must be true that, that is, Solving for gives . Substituting for in the expressions of the three first terms of the sequence, one sees that they are , , and , respectively. The common difference between consecutive terms for this arithmetic sequence is , and therefore, the fourth term is .24Your answer Omitted!In a group of people, percent have brown eyes. Two people are to be selected at random from the group. What is the probability that neither person selected will have brown eyes?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is A.One way to determine the probability that neither person selected will have brown eyes is to count both the number of ways to choose two people at random from the people who do not have brown eyes and the number of ways to choose two people at random from all people, and then compute the ratio of those two numbers.Since percent of the people have brown eyes, there are people with brown eyes, and people who do not have brown eyes. The number of ways of choosing two people, neither of whom has brown eyes, is : there are ways to choose a first person and ways to choose a second person, but there are ways in which that same pair of people could be chosen. Similarly, the number of ways of choosing two people at random from the people is . Therefore, the probability that neither of the two people selected has brown eyes is.Another way to determine the probability that neither person selected will have brown eyes is to multiply the probability of choosing one of the people who does not have brown eyes at random from the people times the probability of choosing one of the people who does not have brown eyes at random from the remaining people after one of the people who does not have brown eyes has been chosen.Since percent of the people have brown eyes, the probability of choosing one of the people who does not have brown eyes at random from the people is . If one of the people who does not have brown eyes has been chosen, there remain people who do not have brown eyes out of a total of people; the probability of choosing one of the people who does not have brown eyes at random from the people is . Therefore, if two people are to be selected from the group at random, the probability that neither person selected will have brown eyes is .25Your answer Omitted!If , what is ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is E.One way to determine the value of is to solve the equation for . Since , start with the equation , and cube both sides to get. Isolate to get , and apply the cube root to both sides of the equation to get .Another way to determine the value of is to find a formula for and then evaluate at Let and solve for : cubing both sides gives , so , and. Therefore, , and .26Your answer Omitted!Which of the following equations best models the data in the table above?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is D.One way to determine which of the equations best models the data in the table is to use a calculator that has a statistics mode to compute an exponential regression for the data.The specific steps to be followed depend on the model of calculator, but can be summarized as follows: Enter the statistics mode, edit the list of ordered pairs to include only the four points givenin the table and perform an exponential regression. The coefficients are, approximately, for the constant and for the base, which indicates that the exponential equation is the result of performing the exponential regression. If the calculator reports a correlation, it should be a number that is very close , to which indicates that the data very closely matches the exponential equation. Therefore, of the given models, best fits the data.Alternatively, without using a calculator that has a statistics mode, one can reason about the data given in the table.The data indicates that as increases, increases; thus, options A and B cannot be candidates for such a relationship. Evaluating options C, D and E at shows that option D is the one that gives a value of that is closest to In the same way, evaluating options C, D and E at each of the other given data points shows that option D is a better model for that one data point than either option C or option E. Therefore, is the best of the given models for the data.27Your answer Omitted!The linear regression model above is based on an analysis of nutritional data from 14 varieties of cereal bars to relate the percent of calories from fat to the percent of calories from carbohydrates . Based on this model, which of the following statements must be true?I. There is a positive correlation between and .II. When percent of calories are from fat, the predicted percent of calories from carbohydrates is approximately .III. The slope indicates that as increases by , decreases by .(A) II only(B) I and II only(C) I and III only(D) II and III only(E) I, II, and IIIExplanationDifficulty: HardThe correct answer is D.Statement I is false: Since , high values of are associated with low values of which indicates that there is a negative correlation between and .Statement II is true: When percent of calories are from fat, and the predicted percent of calories from carbohydrates is .Statement III is true: Since the slope of the regression line is , as increases by , increases by ; that is, decreases by .28Your answer Omitted!The number of hours of daylight, , in Hartsville can be modeled by , where is the number of days after March . The day with the greatest number of hours of daylight has how many more daylight hours than May ? (March and May have days each. April and June have days each.)(A) hr(B) hr(C) hr(D) hr(E) hrExplanationDifficulty: HardThe correct answer is A.To determine how many more daylight hours the day with the greatest number of hours of daylight has than May , find the maximum number of daylight hours possible for any day and then subtract from that the number of daylight hours for May .To find the greatest number of daylight hours possible for any day, notice that the expressionis maximized when , which corresponds to , so. However, for this problem, must be a whole number, as it represents a count of days after March . From the shape of the graph of the sine function, either or corresponds to the day with the greatest number of hours of daylight, and since, the expression is maximized when days after March . (It is not required to find the day on which the greatest number of hours of daylight occurs, but it is days after March ,that is, June .)Since May is days after March , the number of hours of daylight for May is .Therefore, the day with the greatest number of hours of daylight hasmore daylight hours than May .。

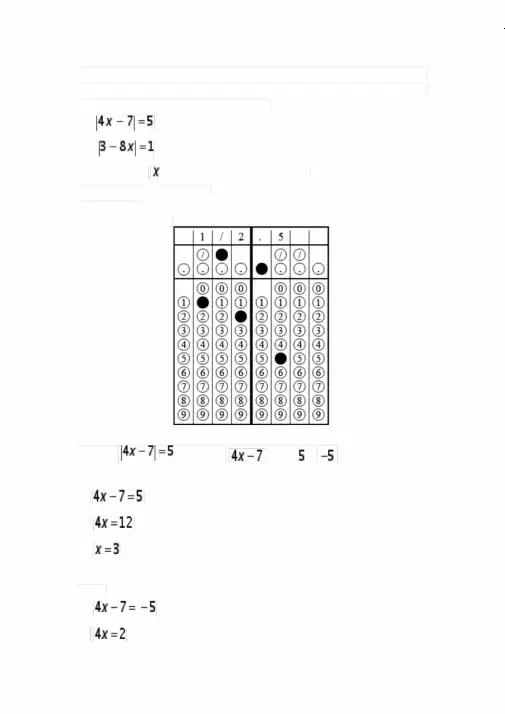
that satisfy the second equation arethat satisfies both equations. That value isThe formula for a cone ‘s surface area is πr2 + πrl. A cone ‘s volume is 1/ 3 πr2h. So if一道SAT 数学题(抛物线)The correct answer is CExplanationmust be the vertex of the parabola. The parabola intersects the , so must be halfway. Of the choices, the only one withcould be the coordinates ofVertical height of triangle = 5 ; horizontal side = 4 ; hypotenuse = 2. n is an integer chosen at random from the set{5, 7, 9, 11 }p is chosen at random from the set{2, 6, 10, 14, 18}A. 0.75DB. 0.76DC. 0.765DD. 0.775Dwhat is the best approximation to the length of arc AB ?A. 9π. The length of the arc is 100/360 of themembers and the chess club hasstudents belong to only one of the two clubs, how manystudents belong to both clubs?Answer ChoicesThe correct answer is CExplanationstand for the number of students who belong to both clubs. Thestudents who are in the chess club only.that. Solving this equation gives belong to both clubs 。

SAT 数学教程I. 解题技巧训练5671 The units digit of 23333 is how much less than the hundredths digit of 1000(A) 1 (B) 2 (C) 3 (D) 4 (E) 52. What is the units digit of 1597365?3. Bob has a pile of poker chips that he wants to arrange in even stacks. If he stacks them in piles of 10, he has 4 chips left over. If he stacks them in piles of 8, he has 2 chips left over. If Bob finally decides to stack the chips in only 2 stacks, how many chips could be in each stack?A. 14B. 17C. 18D. 24E. 344. If x and y are two different integers and the product 35xy is the square of an integer, which of the following could be equal to xy?A. 5B.70C. 105D. 140E. 3505. If x2=y3 and (x-y)2=2x, then y could equal (A) 64 (B) 16 (C) 8 (D) 4 (E) 26. For positive integers p, t, x and y, if p x=t y and x-y=3, which of the following CANNOT equal t?A. 1B. 2C. 4D. 9E. 257. If 3t-3>6s+9 and t-5s<12, and s is a positive integer less than 4, then t could be any of the following EXCEPT A. 6 B. 8 C. 10 D.12 E. 238. If n and p are integers greater than 1 and if p is a factor of both n+3 and n+10, what is the value of p?A. 3B. 7C. 10D. 13E. 309. If x is a positive integer greater than 1, and x3-4x is odd, then x must be(A) even (B) odd (C) prime (D) a factor of 8 (E) divisible by 810.If the graph above is that of f(x), which of the following could be f(x)A. f(x)= 3||xB. f(x)=|3|x C. f(x)=/x/+3 D. f(x)=|x+3| E. f(x)=|3x|11. xy=x+y. If y>2, what are all possible values of x that satisfy the equation above?A. x<0,B. 0<x<1C.0<x<2D.1<x<2E. x>2II. 算术 ――对应知识点训练1. 代数题(1). Karl bought x bags of red marbles for y dollars per bag, and z bag of blue marbles for 3y dollars per bag. If he bought twice as many bags of blue marbles as red marbles, then in terms of y, what was the average cost, in dollars, per bag of marbles? (A)23y (B) 37y (C) 3x-y (D) 2y (E) 6y(2) At this bake sale, Mr. Right sold 30% of his pies to one friend. Mr. Right then sold 60% of the remaining pies to another friend. What percent of his original number of pies did Mr. Right have left?(A) 10% (B) 18% (C) 28% (D) 36% (E) 40%(3) At a track meet, 2/5 of the first-place finishers attended Southport High School, and 1/2 of them were girls. If 2/9 of the first-place finishers who did NOT attend Southport High School were girls, what fractional part of the total number of first-place finishers were boys?(A) 1/9 (B) 2/15 (C) 7/18 (D) 3/5 (E) 2/32. 中位数（4）Number of siblings per student in a preschool classThe table above shows how many students in a class of 12 preschoolers had 0,1,2, or 3 siblings. Later, a new student joined the class, and the average (arithmetic mean) number of siblings per student became equal to the median number of siblings per student. How many siblings did the new student have?A. 0B. 1C. 2D. 3E. 4（5）In a set of eleven different numbers, which of the following CANNOT affect the value of the median?A. Doubling each numberB. Increasing each number by 10C. Increasing the smallest number onlyD. Decreasing the largest number onlyE. Increasing the largest number only（6）. The least and greatest numbers in a list of 7 real numbers are 2 and 20, respectively. The median of the list is 6, and the number 3 occurs most often in the list. Which of the following could be the average (arithmetic mean) of the numbers in the list?I. 7 II. 8.5 III. 10A. I onlyB. I and II onlyC. I and III onlyD. II and III onlyE. I, II and III3. 集合部分(6) Set F consist of all of the prime numbers from 1 to 20 inclusive, and set G consist of all of the odd numbers from 1 to 20 inclusive. If f is the number of values in set F, g is the number of values of in Set G, and j is the number of values in F∪G, which of the following gives the correct value of f(j-g)?A. 4B. 8C. 10D. 11E. 18(7) Set X has x members and set Y has y members. Set Z consists of all members that are in either Set X or Set Y with the exception of the k common members (k>0). Which of the following represents the number of members in set Z?A. x+y+kB. x+y-kC. x+y+2kD. x+y-2kE. 2x+2y-2k(8) Of the 240 campers at a summer camp, 5/6 could swim, if 1/3 of the campers took climbing lessons, what was the least possible number of campers taking climbing lessons who could swim?A. 20B.40C. 80D.120E. 200(9) Set F consist of all of the prime numbers from 1 to 20 inclusive, and set G consist of all of the odd numbers from 1 to 20 inclusive. If f is the number of values in set F, g is the number of values of in Set G, and j is the number of values in F∪G, which of the following gives the correct value of f(j-g)?A. 4B. 8C. 10D. 11E. 184. 排列组合题(10)Mr. Jones must choose 4 of the following 5 flavors of jellybean: apple, berry, coconut, kumquat, and lemon, How many different combinations of flavors can Mr. Jones choose?（11）If the 5 cards shown above are placed in a row so that is never at either end, how many different arrangements are possible?（12）As shown above, a certain design is to be painted using 2 different colors. If 5 different colors are available for the design, how many differently painted designs are possible?A. 10B. 20C. 25D. 60E. 120（13）In the integer 3589 the digits are all different and increase from left to right. How many integers between 4000 and 5000 have digits that are all different and that increased from left to right?（14）.On the map above, X represents a theater, Y represents Chris’s house, and Z represents Peter’s house. Chris walks from his house to Peter’s house without passing the theater and then walks with Peter to the theater and then walks without walking by his own house again. How many different routs can Chris take?（15）In a certain game, 8 cards are randomly placed face-down on a table. The cards are numbered from 1 to 4 with exactly 2 cards having each number. If a player turns over two of the cards, what is the probability that the cards will have the same number?（16）The Acme Plumbing Company will send a team of 3 plumbers to work on a certain job. The company has 4 experienced plumbers and 4 trainees. If a team consists of 1 experienced plumber and 2 trainees, how many different such teams are possible?（17）If p, r, m, n, t and s are six different prime numbers greater than 2, and n=p*r*s*m*n*t, how many positive factors, including 1 and n, does n have?5.数列部分(14) The least integer of a set of consecutive integers is -25. If the sum of these integers is 26, how many integers are in this set? A. 25 B. 26 C.50 D. 51 E. 52(15) 1,2,2,3,3,3,4,4,4,4….All positive integers appear in the sequence above, and each positive integer k appears in the sequence k times. In the sequence, each term after the first is greater than or equal to each of the terms before it. If the integer 12 first appears in the sequence as the n th term, what is the value of n ?(16) The first term of a sequence of numbers is 2. Subsequently, every even term in the sequence is found by subtracting 3 from the previous term, and every odd term in the sequence is found by adding 7 to the previous term. What is the difference between 77th and 79th terms of this sequence?A. 11B. 7C. 4D. 3E. 26.应用题(16) A positive integer is said to be “tri-factorable ” if it is the product of three consecutive integers. How many positive integers less than 1000 are tri-factorable?(17) Tom and Alison are both salespeople. Tom ’s weekly compensation consists of $300 plus 20 percent of his sale. Alison ’s weekly compensation consists of $200 plus 25 percent of her sales. If they both had the same amount of sales and the same compensation for a particular week, what was that compensation, in dollars? (Disregard dollar sign when gridding your answer)(18) To celebrate a colleague ’s graduation, the m coworkers in an office agreed to contribute equally to a catered lunch that costs a total of y dollars. If p of the coworkers fail to contribute, which of the following represents the additional amount, in dollars, that each of the remaining coworkers must contribute to pay for the lunch? A.m y B. p m y - C. p m py - D. m p m y )(- E. )(p m m py -(19) In a certain store, the regular price of a refrigerator is $600. How much money is saved by buying this refrigerator at 20 percent off the regular price rather than buying it on sale at 10 percent off the regular price with an additional discount of 10 percent off the sale price?(A) $6 (B) $12 (C) $24 (D) $54 (E) $607.整除，最小公倍数，余数问题(20) When a is divided by 7, the remainder is 4. When b is divided by 3, the remainder is 2. If 0<a <24 and 2<b <8, which of the following could have a remainder of 0 when divided by (A)b a (B) a b (C) a-b (D) a+b (E) ab(21) The alarm of Clock A rings every 4 minutes, the alarm of Clock B rings every 6 minutes, and the alarm of Clock C rings every 7 minutes. If the alarms of all three clocks ring at 12:00 noon, the next time at which all the alarms will ring at exactly the same time isA. 12:28 P.M.B. 12:56 P.M.C. 1:24 P.M.D. 1:36 P.M.E. 2:48 P.M.(22) If a, b, and c are distinct positive integers, and 10% of abc is 5, then a+b could equalA. 1B. 3C. 5D. 6E. 25(23) On 5 math tests, Gloria had an average score of 86. If all test scores are integers, what is the lowest average score average score Gloria can receive on the remaining 3 tests if she wants to finish the semester with an average score of 90 or higher?A. 90B. 92C. 94D. 96E. 97 (24) If ky 4 is the cube of an integer greater than 1, and k2=y, what is the least possible value of y? A. 1 B. 2 C. 4 D. 6 E. 27III 代数问题(1) The height of the steam burst of a certain geyser varies with the length of time since the previous steam burst. The longer the time since the last burst, the greater the height of the steam burst. If t is the time in hours since the previous steam burst and H is the height in meters of the steam burst, which of the following could express the relationship of t and H ?A ． H(t)= 21(t-7) B. H(t)= 72 t C. H(t)=2-(t-7) D. H(t)= 7-2t E. H(t)= t72（2） 4)The above graph could represent which of the following inequalities?A. y ≤x 1B. y< (21)xC. y ≥x 1 D . y ≥(21)x E . y ≥x -1/2 （3）The change in temperature is a function of the change in altitude in such a way that as the altitude increases, so dose the change in the temperature. For example, a gain of 1980 feet causes a 60F, which of the following could be the relationship of a and T?A. T(a)= a/300B. T(a)= a-330C. T(a)=330/aD. T(a)=330-aE. T(a)=330a（4） Let f(x) be defined as the least integer greater than x/5. Let g(x) be defined as the greatest integer less than x/5. What is the value of g(18)+f(102)? A. 21 B. 22 C. 23 D. 24 E. 25（5）Radioactive substance T-36 dose not stay radioactive forever. The time it takes for half of the element to decay is called a half-life. If, before any decay takes place, there is 1 gram of radioactive substance T-36, and the half-life is 7 days, how much remains after 28 days? A. 7-28 B. 2-4 C. 2-2 D. 1-28 E. 22(6) Luke purchased an automobile for $5000, and the value of the automobile decreases by 20 percent each year. The value, in dollars, of the automobile n years from the date of purchase is given by the function V , where V(n)=5000*(0.8)n . how many years from the date of purchase will the value of the automobile be $ 3200? A. 1 B. 1 C. 3 D. 4 E. 5(7) The cost of maintenance on an automobile increases each year by 10 percent, and Andrew paid $300 this year for maintenance on his automobile. If the cost c for maintenance on Andrew ’s automobile n years from now is given by the function c(n)=300x n , what is the value of x ?A. 0.1B. 0.3C. 1.1D. 1.3E. 30(8) h(t)= c- (d-4t)2At time t=0, a ball thrown upward from an initial height of 6 feet. Until the ball hit the ground, its height, in feet, after t seconds was given by the function h above, in which c and d are positive constants. If the ball reached its maximum height of 106 feet at time t=2.5, what was the height, in feet, of the ball at time t=1?(9) If k, n, x and y are positive numbers satisfying x -4/3 = k -2 and y 4/3 =n 2, what is (xy ) -2/3 in terms of n and k ? A. nk 1 B. k n C. nk D. nk E. 1(10)The figures above show the graphs of the function f and g . The function f is defined by f(x)=x 3-4x . the function g is defined by g(x)=f(x+h)+k , where h and k are constants. What is the value of hk ?A. -6B. -3C. -2D.3E. 6(11) Let [x] be defined as [x]=x 2-x for all values of x. if [a]= [a-2]. What is the value of a?A. 1B. 0.5C. 1.5D. 1.125E. 3(12) If k and h are constants and x 2+kx+7 is equivalent to (x+1)(x+h), what is the value of k ?A. 0B. 1C. 7D. 8E. cannot be determined(13) For all numbers a and b, let a^b be defined by a^b= ab+ a +b. For all numbers x, y, and z, which of the following must be true?I. x^y= y^xII. (x-1)^ (x+1)= (x^x) -1III. x^ (y+z) = (x^y) + (x ^ z)A. I onlyB. II onlyC. III onlyD. I and II onlyE. I, II and III(14)The graph above shows the function g, where g(x)= k(x+3)(x-3) for some constant k. If g(a- 1.2)= 0 and a>0, what is the value of a?(15) (x-8)(x-k)= x2-5kx+mIn the equation above, k and m are constants. If the equation is true for all value of x, what is the value of m?A. 8B. 16C. 24D. 32E. 40(16) A certain function f has the property that f(x+y)=f(x)+f(y) for all values of x and y. which of the following statements must be true when a=b?I. f(a+b)= 2f(a) II. f(a+b)=[f(a)]2 III. f(a)+f(b)=f(2a)A. NoneB. I onlyC. I and III onlyD. II and III onlyE. I, II and III（17）.The shaded region in the figure above is bounded by the x-axis, the line x=4, and the graph of y=f(x). if the point (a, b) lies in the shaded region, which of the following must be true?I. a≤4 II. b≤a III. b≤f(a)(A) I only(B) III only(C) I and II only(D) I and III only(E) I, and II and III（18）The figure above shows the graphs of y=x2 and y=a-x2 for some constant a. if the length of PQ is equal to 6, what is the value of a? A. 6 B. 9 C. 12 D. 15 E. 18（19）In the figure above, ABCD is a rectangle. Points A and C lie on the graph of y=px3, where p is a constant,. If the area of ABCD is 4, what is the value of p?IV 几何部分（1）Each of the small squares in the figure above has an area of 4. If the shortest side of the triangle is equal in length to 2 sides of a small square, what is the area of the shaded triangle?A. 160B. 40C. 24D. 20E. 16（2）.In the figure above, a shaded polygon which has equal sides and angles is partially covered with a sheet of blank paper. If x+y=80, how many sides does the polygon have?A. 10B. 9C. 8D. 7E. 6（3）The area of rectangle ABCD is 96, and AD=2/3(AB). Points X and Y are midpoints of AD and BC, respectively. If the 4 shaded triangles are isosceles, what is the perimeter of the unshaded hexagon? A. 16 B.8+62 C. 24 D. 8+162 E. 16+242（4）In the figure above, what is the value of c in terms of a and b?A. a+3b-180B. 2a+2b-180C. 180-a-bD. 360-a-bE. 360-2a-3b（5）The figure above shows an arrangement of 10 squares, each with side of length k inches. The perimeter of the figure is p inches. The area of the figure is a square inches. If p=a, what is the value of k?（6）.One end of an 80-inch-long paper strip is shown in the figure above. The notched edge, shown in bold, was formed by removing an equilateral triangle from the end of each 4-inch length on one edge of the paper strip. What is the total length, in inches, of the bold notched edge on the 80-inch paper strip?（7）.At a beach, a rectangular swimming area with dimensions x and y meters and a total area of 4000 square meters is marked off on three sides with rope, as shown above, and bounded on the fourth side by the beach. Additionally, rope is used to divide the area into three smaller rectangular sections. In terms of y, what is the total length, in meters, of the rope that is need both to bound the three sides of the area and to divide it into sections?A. y+ 4000/yB. y+16000/yC. y+16000/(3y)D. 3y+ 8000/(3y)E. 3y+ 16000/(3y)（8）If a triangle ABC has AB=7 and BC=7, then the difference between the greatest and least possible integer values of AC is A. 11 B. 12 C. 13 D. 14 E. 15（9）In a triangle PQR, the length of side QR is 12 and the length of side PR is 20. What is the greatest possible integer length of side PQ?A. 9B. 16C. 25D. 27E. 31（10）.In the figure above, arc SBT is one quarter of a circle with center R and radius 6. If the length plus the width of rectangle ABCR is 8, then the perimeter of the shaded region isA. 8+3πB. 10+3πC. 14+ 3πD. 1+6πE. 12+6π（11）In the figure above, QR is the arc of a circle with center P. If the length of the arc QR is 6π,what is the area of sector PQR?A. 108πB. 72πC. 54πD. 36πE. 9π（12）.The figure above consists of two circles that have the same center. If the shaded area is 64π square inches and the smaller circle has a radius of 6 inches, what is the radius, in inches, of the larger circle?（13）.The figure above shows part of a circle whose circumference is 45. If arcs of length 2 and length b continue to alternate around the entire circle so that there are 18 arcs of each length, what is the degree measure of each of the arcs of length b?A. 40B. 60C. 100D. 160E. 20o（14）In a certain machine, a gear makes 12 revolutions per minute. If the circumference of the gear is 3πinches, approximately how many feet will the gear turn in an hour?A. 6782B. 565C. 113D. 108E. 9（15）In the xy-coordinate plane, the graph of x=y2-4 intersects line l at (0, p) and (5, t). what is the greatest possible value of the slope of line l?（16）The coordinates for point A are (-2, 2) and the coordinates for point B are (4, 8). If line CD is parallel to the line AB, what is the slope of line CD?A. -1B. 0C. 1D. 2E. 4（17）Rectangle ABCD lies in the xy-coordinate plane so that its sides are not parallel to the axes. What is the product of the slopes of all four sides of rectangle ABCD?A. -2B. -1C. 0D. 1E. 2（18）Alice and Corinne stand back-to-back. They each take 10 steps in opposite directions away from each other and stop. Alice then turns around, walks toward Corinne, and reaches her in 17 steps. The length of one of Alice’s steps is how many times the length of one of Corinne’s steps? (All of Alice’s steps are the same length and all of Corinne’s steps are the same length.)（19）.Line m (not shown) passes through O and intersects AB between A and B. what is one possible value of the slope of line m?立体几何部分：（1）In figure above, S is the midpoint of RT. What is the area of the shaded triangle?A. 14B. 16C. 265D. 18E. 46（2）A ball with a volume of 18 cubic inches is dropped into an aquarium that is partially filled with water. If the base of the aquarium measures 12 inches by 6 inches, how many inches will the level of water rise after the ball is submerged?A. 0.25 inchesB. 0.5 inchesC. 1 inchesD. 4 inchesE. 6 inches.（3）In the cube shown above, point B, C, and E are midpoints of three of the edges. Which of the following angles has the least measure?A.∠ XAYB. ∠ XBYC. ∠ XCYD. ∠ XDYE. ∠ XEY（4）.The pyramid shown above has altitude h and a square base of side m. The four edges that meet at V , the vertex of the pyramid, each have length e. If e=m, what is the value of h in terms of m? A. 2m B. 23m C. m D. 32m E. 2m（5）.The cube shown above has edges of length 2, and A and B are midpoints of two of the edges. What is the length of AB? A. 2 B. 3 C. 5 D. 6 E. 10（6）A sphere of radius r inside a cube touches each one of the six sides of the cube. What is the volume of the cube, in terms of r?A. r 3B. 2 r 3C. 4 r 3D.34πr 3 E. 8 r 3（7）A cube with volume 8 cubic centimeters is inscribed in a sphere so that each vertex of the cube touches the sphere. What is the length of the diameter, in centimeters of the sphere? A. 2 B. 6 C. 2.5 D. 23 E. 4。

SAT Subject Test Practice - Results SummaryMathematics Level 21Your answer Omitted!What is the distance in space between the points with coordinates and ? (A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is D.The distance between the points with coordinates and is given by the distance formula: .Therefore, the distance between the points with coordinates and is:,which simplifies to .2Your answer Omitted!If , what value does approach as gets infinitely larger?(A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is E.One way to determine the value that approaches as gets infinitely larger is to rewrite the definition of the function to use only negative powers of and then reason about the behavior of negative powers of as gets infinitely larger. Since the question is only concerned with what happens to as gets infinitely larger, one can assume that is positive. For , the expression is equivalent to the expression . As gets infinitelylarger, the expression approaches the value , so as gets infinitely larger, the expressionapproaches the value . Thus, as gets infinitely larger, approaches .Alternatively, one can use a graphing calculator to estimate the height of the horizontal asymptote for the function . Graph the function on an interval with “large”, say, from to .By examining the graph, the all seem very close to . Graph the function again, from, say, to .The vary even less from . In fact, to the scale of the coordinate plane shown, the graph of the function is nearly indistinguishable from the asymptotic line . This suggests that as gets infinitely larger, approaches , that is, .Note: The algebraic method is preferable, as it provides a proof that guarantees that the value approaches is . Although the graphical method worked in this case, it does not provide a complete justification; for example, the graphical method does not ensure that the graph resembles a horizontal line for “very large” such as .3Your answer Omitted!If is a factor of , then(A)(B)(C)(D)(E)ExplanationDifficulty: EasyThe correct answer is A.By the Factor Theorem, is a factor of only when is a root ofthat is, , which simplifies to . Therefore, .Alternatively, one can perform the division of by and then find a value for so that the remainder of the division is .Since the remainder is , the value of must satisfy . Therefore, .4Your answer Omitted!Alison deposits into a new savings account that earns percent interest compounded annually. If Alison makes no additional deposits or withdrawals, how many years will it take for the amount in the account to double?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumAfter year, the amount in the account is equal to . After years, the amount isequal to , and so on. After years, the amount is equal to . You needto find the value of for which . There are several ways to solve this equation. You can use logarithms to solve the equation as follows.Since , it will take more than years for the amount in the account to double. Thus, you need to round up to .Another way to find is to use your graphing calculator to graph and . From the answer choices, you know you need to set the viewing window with values from to about and values extending just beyond . The of the point of intersection is approximately . Thus you need to round up to .5Your answer Omitted!In the figure above, when is subtracted from , what is the length of the resultant vector?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe resultant of can be determined by. The length of the resultant is:6Your answer Omitted!In the -plane, what is the area of a triangle whose vertices are , , and ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt is helpful to draw a sketch of the triangle:The length of the base of the triangle is and the height of the triangle is . Therefore, the area of the triangle is . The correct answer is B.7Your answer Omitted!A right circular cylinder has radius and height . If and are two points on its surface, what is the maximum possible straight-line distance between and ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe maximum possible distance occurs when and are on the circumference of opposite bases:You can use the Pythagorean Theorem:The correct answer is (B).8Your answer Omitted!Note: Figure not drawn to scale.In the figure above, and the measure of is . What is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThere are several ways to solve this problem. One way is to use the law of sines. Since ,the measure of is and the measure of is . Thus, and . (Make sure your calculator is in degree mode.)You can also use the law of cosines:Since is isosceles, you can draw the altitude to the triangle.9Your answer Omitted!The function is defined by for .What is the difference between the maximum and minimum values of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt is necessary to use your graphing calculator for this question. First graph the function. It is helpful to resize the viewing window so the -values go fromto . On this interval the maximum value of is and the minimum value of is. The difference between these two values is , which rounds to .10Your answer Omitted!Suppose the graph of is translated units left and unit up. If the resulting graph represents , what is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumIt may be helpful to draw a graph of and .The equation for is . Therefore,. The correct answer is B.11Your answer Omitted!A sequence is recursively defined by , for . If and , what is the value of ?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe values for and are given. is equal to . is equal to. is equal to . is equal to.If your graphing calculator has a sequence mode, you can define the sequence recursively and find the value of . Let , since the first term is . Define . Let , since we have to define the first two terms and . Then examining a graph or table, you can find .12Your answer Omitted!The diameter and height of a right circular cylinder are equal. If the volume of the cylinder is , what is the height of the cylinder?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is A.To determine the height of the cylinder, first express the diameter of the cylinder in terms of the height, and then express the height in terms of the volume of the cylinder.The volume of a right circular cylinder is given by , where is the radius of the circular base of the cylinder and is the height of the cylinder. Since the diameter and height are equal, . Thus . Substitute the expression for in the volume formula to eliminate :. Solving for gives . Since the volume of the cylinder is , theheight of the cylinder is .13Your answer Omitted!If , then(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is E.One way to determine the value of is to apply the sine of difference of two angles identity: . Since and , the identity gives . Therefore, .Another way to determine the value of is to apply the supplementary angle trigonometric identity for the sine: . Therefore, .14Your answer Omitted!A line has parametric equations and , where is the parameter. The slope of the line is(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is B.One way to determine the slope of the line is to compute two points on the line and then use the slope formula. For example, letting gives the point on the line, and letting gives the point on the line. Therefore, the slope of the line is equal to .Alternatively, one can express in terms of . Since and , it follows that . Therefore, the slope of the line is .15Your answer Omitted!What is the range of the function defined by ?(A) All real numbers(B) All real numbers except(C) All real numbers except(D) All real numbers except(E) All real numbers between andExplanationDifficulty: MediumThe correct answer is D.The range of the function defined by is the set of such thatfor some .One way to determine the range of the function defined by is to solve the equationfor and then determine which correspond to at least one . To solve for , first subtract from both sides to get and then take the reciprocal of both sides to get . The equation shows that for anyother than , there is an such that , and that there is no such for . Therefore, the range of the function defined by is all real numbers except .Alternatively, one can reason about the possible values of the term . The expression can take on any value except , so the expression can take on any value except . Therefore, the range of the function defined by is all real numbers except .16Your answer Omitted!The table above shows the number of digital cameras that were sold during a three-day sale. The prices of models , , and were , , and , respectively. Which of the following matrix representations gives the total income, in dollars, received from the sale of the cameras for each of the three days?(A)(B)(C)(D)(E)ExplanationDifficulty: MediumThe correct answer is C.A correct matrix representation must have exactly three entries, each of which represents the total income, in dollars, for one of the three days. The total income for Day is given by the arithmetic expression , which is the single entry of the matrix product; in the same way, the total income for Day is given by, the single entry of ; and the total income for Day is given by , the single entry of. Therefore, the matrix representationgives the total income, in dollars, received from the sale of the cameras for each of the three days. Although it is not necessary to compute the matrix product in order to answer the question correctly, equals .17Your answer Omitted!The right circular cone above is sliced horizontally forming two pieces, each of which has the same height. What is the ratio of the volume of the smaller piece to the volume of the larger piece?(A)(B)(C)(D)(E)ExplanationDifficulty: HardIt is helpful to label the figure.The top piece is a cone whose height is one-half the height of the original cone . Using the properties of similar right triangles, you should realize the radii of these two cones must be in the same ratio. So if the top cone has radius , the original cone has radius .The volume of the top piece is equal to . The volume of the bottom piece is equal to the volume of the original cone minus the volume of the top piece.The ratio of the volume of the smaller piece to the volume of the larger piece is .18Your answer Omitted!In the figure above, is a regular pentagon with side of length . What is the -coordinate of ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe sum of the measures of the interior angles of a regular pentagon is equal to . Each interior angle has a measure of . Using supplementary angles, has a measure of . You can use right triangle trigonometry to find the -coordinate of point .Since , is about . Since the length of each side of the pentagon is , the -coordinate of point is . Putting the information together tells us that the -coordinate of point is . The correct answer is (B).19Your answer Omitted!For a class test, the mean score was , the median score was , and the standard deviation of the scores was . The teacher decided to add points to each score due to a grading error. Which of the following statements must be true for the new scores?I.The new mean score is .II.The new median score is .III.The new standard deviation of the scores is .(A) None(B) only(C) only(D) and only(E) , , andExplanationDifficulty: HardFor this type of question you need to evaluate each statement separately. Statement is true. If you add to each number in a data set, the mean will also increase by . Statement is also true. The relative position of each score will remain the same. Thus, the new median score will be equal tomore than the old median score. Statement is false. Since each new score is more than the old score, the spread of the scores and the position of the scores relative to the mean remain the same. Thus, the standard deviation of the new scores is the same as the standard deviation of the old scores.20Your answer Omitted!A game has two spinners. For the first spinner, the probability of landing on blue is . Independently, for the second spinner, the probability of landing on blue is What is the probability that the first spinner lands on blue and the second spinner does not land on blue?(A)(B)(C)(D)(E)ExplanationDifficulty: HardSince the two events are independent, the probability that the first spinner lands on blue and the second spinner does not land on blue is the product of the two probabilities. The first probability is given. Since the probability that the second spinner lands on blue is the probability that thesecond spinner does not land on blue is Therefore, . The correct answer is (E).21Your answer Omitted!In January the world’s population was billion. Assuming a growth rate of percent per year, the world’s population, in billions, for years after can be modeled by theequation . According to the model, the population growth from January to January was(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is C.According to the model, the world’s population in January was and in January was . Therefore, according to the model, the population growth from Januaryto January , in billions, was , or equivalently,.22Your answer Omitted!What is the measure of one of the larger angles of a parallelogram in the that has vertices with coordinates , , and ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is C.First, note that the angle of the parallelogram with vertex is one of the two larger angles of the parallelogram: Looking at the graph of the parallelogram in the makes this apparent. Alternatively, the sides of the angle of the parallelogram with vertex are a horizontal line segment with endpoints and and a line segment of positive slope with endpoints and that intersects the horizontal line segment at its left endpoint , so the angle must measure more than Since the sum of the measures of the four angles of aparallelogram equals , the angle with vertex must be one of the larger angles.One way to determine the measure of the angle of the parallelogram with vertex is to apply the Law of Cosines to the triangle with vertices , , and . The length of the twosides of the angle with vertex are and; the length of the side opposite the angle is . Let represent the angle with vertex and apply the Law of Cosines: , so. Therefore, the measure of one of thelarger angles of the parallelogram is .Another way to determine the measure of the angle of the parallelogram with vertex is to consider the triangle , , and . The measure of the angle of this triangle with vertex is less than the measure of the angle of the parallelogram with vertex . The angleof the triangle has opposite side of length and adjacent side of length , so the measure of this angle is . Therefore, the measure of the angle of the parallelogram with vertex is .Yet another way to determine the measure of the angle of the parallelogram with vertex is to use trigonometric relationships to find the measure of one of the smaller angles, and then use the fact that each pair of a larger and smaller angle is a pair of supplementary angles. Consider the angle of the parallelogram with vertex ; this angle coincides with the angle at vertex of the right triangle with vertices at , , and , with opposite side of lengthand adjacent side of length , so the measure of this angle is . This angle, together with the angle of the parallelogram with vertex , form a pair of interior angles on the same side of a transversal that intersects parallel lines, so the sum of the measures of the pair of angles equals . Therefore, the measure of the angle of the parallelogram with vertex is.23Your answer Omitted!For some real number , the first three terms of an arithmetic sequence are, and . What is the numerical value of the fourth term?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is E.To determine the numerical value of the fourth term, first determine the value of and then apply the common difference.Since , and are the first three terms of an arithmetic sequence, it must be true that, that is, Solving for gives . Substituting for in the expressions of the three first terms of the sequence, one sees that they are , , and , respectively. The common difference between consecutive terms for this arithmetic sequence is , and therefore, the fourth term is .24Your answer Omitted!In a group of people, percent have brown eyes. Two people are to be selected at random from the group. What is the probability that neither person selected will have brown eyes?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is A.One way to determine the probability that neither person selected will have brown eyes is to count both the number of ways to choose two people at random from the people who do not have brown eyes and the number of ways to choose two people at random from all people, and then compute the ratio of those two numbers.Since percent of the people have brown eyes, there are people with brown eyes, and people who do not have brown eyes. The number of ways of choosing twopeople, neither of whom has brown eyes, is : there are ways to choose a first person andways to choose a second person, but there are ways in which that same pair of people could bechosen. Similarly, the number of ways of choosing two people at random from the people is. Therefore, the probability that neither of the two people selected has brown eyes is.Another way to determine the probability that neither person selected will have brown eyes is to multiply the probability of choosing one of the people who does not have brown eyes at random from the people times the probability of choosing one of the people who does not have brown eyes at random from the remaining people after one of the people who does not have brown eyes has been chosen.Since percent of the people have brown eyes, the probability of choosing one of the people who does not have brown eyes at random from the people is . If one of the people who does not have brown eyes has been chosen, there remain people who do not have brown eyes out of a total of people; the probability of choosing one of the people who does not have brown eyes at random from the people is . Therefore, if two people are to be selected from the group at random, the probability that neither person selected will have brown eyes is.25Your answer Omitted!If , what is ?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is E.One way to determine the value of is to solve the equation for . Since , start with the equation , and cube both sides to get. Isolate to get , and apply the cube root to both sides of the equation to get .Another way to determine the value of is to find a formula for and then evaluate at Let and solve for : cubing both sides gives , so , and. Therefore, , and .26Your answer Omitted!Which of the following equations best models the data in the table above?(A)(B)(C)(D)(E)ExplanationDifficulty: HardThe correct answer is D.One way to determine which of the equations best models the data in the table is to use a calculator that has a statistics mode to compute an exponential regression for the data.The specific steps to be followed depend on the model of calculator, but can be summarized as follows: Enter the statistics mode, edit the list of ordered pairs to include only the four points given in the table and perform an exponential regression. The coefficients are, approximately, for the constant and for the base, which indicates that the exponential equation is the result of performing the exponential regression. If the calculator reports a correlation, it should be a number that is very close , to which indicates that the data very closely matches the exponential equation. Therefore, of the given models, best fits the data.Alternatively, without using a calculator that has a statistics mode, one can reason about the data given in the table.The data indicates that as increases, increases; thus, options A and B cannot be candidates for such a relationship. Evaluating options C, D and E at shows that option D is the one that gives a value of that is closest to In the same way, evaluating options C, D and E at each of the other given data points shows that option D is a better model for that one data point than either option C or option E. Therefore, is the best of the given models for the data.27Your answer Omitted!The linear regression model above is based on an analysis of nutritional data from 14 varieties of cereal bars to relate the percent of calories from fat to the percent of calories from carbohydrates . Based on this model, which of the following statements must be true?I.There is a positive correlation between and .II.When percent of calories are from fat, the predicted percent of calories from carbohydrates is approximately .III.The slope indicates that as increases by , decreases by .(A) II only(B) I and II only(C) I and III only(D) II and III only(E) I, II, and IIIExplanationDifficulty: HardThe correct answer is D.Statement I is false: Since , high values of are associated with low values of which indicates that there is a negative correlation between and .Statement II is true: When percent of calories are from fat, and the predicted percent of calories from carbohydrates is .Statement III is true: Since the slope of the regression line is , as increases by ,increases by ; that is, decreases by .28Your answer Omitted!The number of hours of daylight, , in Hartsville can be modeled by , where is the number of days after March . The day with the greatest number of hours of daylight hashow many more daylight hours than May ? (March and May have days each. April and June have days each.)(A) hr(B) hr(C) hr(D) hr(E) hrExplanationDifficulty: HardThe correct answer is A.To determine how many more daylight hours the day with the greatest number of hours of daylight has than May , find the maximum number of daylight hours possible for any day and then subtract from that the number of daylight hours for May .To find the greatest number of daylight hours possible for any day, notice that the expression is maximized when , which corresponds to , so. However, for this problem, must be a whole number, as it represents a count of days after March . From the shape of the graph of the sine function, either orcorresponds to the day with the greatest number of hours of daylight, and since, the expression is maximized when days after March . (It is not required to find the day on which the greatest number of hours of daylight occurs, but it is days after March ,that is, June .)Since May is days after March , the number of hours of daylight for Mayis .Therefore, the day with the greatest number of hours of daylight hasmore daylight hours than May .。

sat数学考题你们知道〔sat〕考试中有数学部分，那么sat数学具体考试内容是什么呢?下面是深圳我为大家整理的关于sat数学考题的相关资料，希望帮到大家。

sat数学考题1.数学运算方面增加了连续运算、正向增量指数运算、集合论中的并集、交集及素的概念和简单计算;2.在代数和函数的知识上，增加了值概念、有理数的等式与不等式、正负指数的计算与平方根的概念、正比和反比的变量关系、函数表达式、函数的域与围的知识、函数与简单物理模型的表达关系、线性函数及二次方程式;3.在几何及度量方面，加入了特别三角形的特征分析、多种切线特征知识、简单的坐标几何学、图形与函数的互相转换与表达等等;难题方面增加了数据分析、简单的矩阵、统计及概率分析的试题。

sat数学如何备考1.在SAT数学考试时，一定做到不要跳步!随时铭记：时间一定够用，正确率是重中之重。

作为中国考生，从小我们就学习口算，背诵九九乘法表。

多年的学习让我们做题时常常会为了节约时间而心算口算，而且十分相信自己的计算结果。

这样很可能导致的结果就是会产生一些计算的小错误。

毕竟SAT数学考试中大部分的题都可以使用计算器，全程也都配有草稿纸供考生进行演算。

因此，"好脑子不如烂笔头'，做题时不要过于相信自己的心算能力，也不用着急做题。

一道一道慢慢计算，保证正确率!2.其次，审题一定要认真!关于大多数中国考生来说，如果把整套数学考题都翻译成中文，或许很多同学都能轻松考到满分。

因此，语言的差异在考试中也是一个潜在的绊脚石。

的老师们贴心地收集整理了详尽的数学词汇大全，以及各大小要点考点的中英文释义。

考生可以在考试前仔细阅读，记忆自己不太把握的词汇和概念。

3.在对单词熟练掌握后，面对新SAT数学的题目，虽然部分题目可以使用计算器。

但是很多同学对自己的心算有着充分的自信，即便是复杂的多项式运算要会懒得动手算，脑子里算一算就贸然选了答案，结果多数会出现错误，而这样的非知识错误经常会造成几十分到几百分的失分。

新SAT(redesigned SAT)的官方样题已经公布有一段时间了。

这次公布的题目数量远远超过4月份，因此得以让我们仔细窥探新SAT的考察意图及考试内容。

经过仔细分析，我们发现新SAT数学变革巨大，显示出主办机构对整个考试思路的全新想法。

一、新SAT改革及数学考试的宗旨相对于现SAT数学侧重以过去为主——考察学生学过什么，新SAT数学的考察侧重于以将来为主——学生将来会需要什么。

因此，新SAT数学舍弃和新增的考察内容都是学生在将来的大学学习或日后工作中会经常用到的知识点。

以这一最高原则为统率，新SAT数学的改革可谓大刀阔斧。

下面我们就一起来看一下新SAT的具体改革内容及应对策略。

二、新SAT数学考察内容的变化通过分析新SAT官方样题，对照现行SAT数学的考试结构，我们将新SAT数学的变化罗列如下：新SAT数学考察内容的变化A. 通过上表我们不难发现，新SAT数学删去了大多数算术部分的内容，只保留了一小部分与数据分析密切相关的内容(如分数、比率、比例、百分比等)放在problem solving and data(数据统计与分析)中。

以往中国学生出错较多的排列组合问题也因此消失，这无疑是一个好消息。

关于整数、小数、奇偶、质数、合数、数轴等问题也没有在新样题中出现。

B. 新SAT数学中的代数部分相当于比现在扩充了整整一倍，其中仅线性函数与线性方程一项就单独占了一个部分(heart of algebra)，这是因为这部分也与数据统计与分析密切相关。

在数据图表中，数据的趋势经常出现近似规律的线性增长或线性下降。

另外，线性方程也在日常应用中频频现身，使得一元一次方程的内容也在其中占据很大篇幅。

二次函数、一元二次方程、指数函数及其他非线性函数被归入第三大部分(passport to advanced math)，《官方指南》指出，新些内容是考生将来进入理工科领域(STEM：Science, Technology, Engineering, Math)必不可少的基础知识，要为将来学习微积分和高级统计做准备。