下载文档原格式
初二数学初中数学综合库试题答案及解析1.如图，一次函数图象经过点A，且与正比例函数y=－x的图象交于点B，则该一次函数的表达式为（）A．y=－x+2B．y="x+2"C．y=x－2D．y=－x－2【答案】B【解析】略2.如图，四边形ABCD是正方形，AC、BD交于点O．则下列结论中错误的是（）A．∠1＝∠2B．AD＝BDC．AC⊥BDD．AD＝AB【答案】B【解析】在Rt△DAB中，直角边AD不等于斜边DB．3.如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于的长为半径画弧，两弧相交于C、D，连接CD，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）A．矩形B．菱形C．正方形D．等腰梯形【答案】B【解析】由作图过程可知AC＝BC＝AD＝BD，所以四边形ADBC是菱形．故选B．4.已知一次函数y＝kx－4的图象经过点P（2，－1），则函数y＝kx－4的解析式为（）A．B．C．D．【答案】A【解析】把x＝2，y＝－1代入y＝kx－4，得－1＝2k－4，解得，∴．5. (2014四川广安)直线y＝3x＋2沿y轴向下平移5个单位，则平移后直线与y轴的交点坐标为________．【答案】(0，－3)【解析】直线y＝3x＋2沿y轴向下平移5个单位后对应的解析式为y＝3x＋2－5，即y＝3x－3，当x＝0时，y＝－3，即与y轴交点坐标为(0，－3)．6.已知一次函数的图象经过(－4，15)，(6，－5)两点，求一次函数的解析式．【答案】设一次函数的解析式为y＝kx＋b(k≠0)．∵y＝kx＋b(k≠0)的图象经过点(－4，15)和点(6，－5)，∴解得∴一次函数的解析式为y＝－2x＋7．【解析】先设一次函数的解析式为y＝kx＋b(k≠0)，因为它的图象经过(－4，15)，(6，－5)两点，所以和适合y＝kx＋b，从而得到关于k、b的方程组，解方程组可求出待定系数k和b的值．再代回原设即可．7.把多项式分解因式，下列结果正确的是（）．A．B．C．D．【答案】D．【解析】利用公式即可得答案．故答案选D．【考点】利用公式进行因式分解．8. A，B两点在反比例函数图像上，则（）A．B．C．D．无法确定【答案】C．【解析】分别把A，B代入可得，，所以，故答案选C．【考点】反比例函数图象上点的坐标的特征．9.如图所示，已知△ABC的周长是20，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是．【答案】30.【解析】如图，连接OA，∵OB、OC分别平分∠ABC和∠ACB，∴点O到AB、AC、BC的距离都相等，∵△ABC的周长是20，OD⊥BC于D，且OD=3，∴S=×20×3=30．△ABC【考点】角平分线的性质．10.（12分）观察下列图形的变化过程，解答以下问题：如图，在△ABC中，D为BC边上的一动点（D点不与B、C两点重合）．DE∥AC交AB于E 点，DF∥AB交AC于F点．（1）试探索AD满足什么条件时，四边形AEDF为菱形，并说明理由；（2）在（1）的条件下，△ABC满足什么条件时，四边形AEDF为正方形．为什么？【答案】（1）AD平分∠EAF，见解析；（2）当△ABC为直角三角形，∠BAC=90°时，【解析】（1）当AD平分∠EAF时，四边形AEDF为菱形，首先由题意推出四边形AEDF为平行四边形，然后根据角平分线的性质和平行线的性质推出∠EAD=∠FDA，∠EAD=∠FAD，通过等量代换求出∠FAD=∠FDA，确定AF=DF后，即可推出结果；（2）当△ABC为直角三角形，∠BAC=90°时，四边形AEDF为正方形，首先根据（1）所推出的结论四边形AEDF为菱形，通过正方形的判定定理（一个内角为直角的菱形为正方形），即可推出结论．试题解析：（1）当AD平分∠EAF时，四边形AEDF为菱形，∵DE∥AC，DF∥AB，∴四边形AEDF为平行四边形，∴∠EAD=∠FDA，∵AD平分∠EAF，∴∠EAD=∠FAD，∴∠FAD=∠FDA，∴AF=DF，∴四边形AEDF为菱形；（2）当△ABC为直角三角形，∠BAC=90°时，四边形AEDF为正方形，理由：由（1）知，四边形AEDF为菱形，∵∠BAC=90°，∴四边形AEDF为正方形．【考点】正方形的判定；平行四边形的判定与性质；菱形的判定．11.解方程组：．【答案】．【解析】利用加减消元法求出解即可．试题解析：由②得：y=3x-11③，将③代入①：2x+9x-33=0，解得：x=3，把x=3代入③得：y=-2，则原方程组的解是．【考点】解二元一次方程组．12.在ΔABC中，∠ABC的平分线与在∠ACE的平分线相交于点D．（1）若∠ABC=60°，∠ACB=40°，求∠A和∠D的度数．（2）由（1）小题的计算结果，猜想，∠A和∠D有什么数量关系，并加以证明．【答案】（1）∠A=80°，∠D=40°；（2）∠A=2∠D，证明见解析．【解析】（1）根据三角形内角和定理和角平分线的性质，已知∠ABC=60°，∠ACB=40°，易求∠A和∠D度数．（2）根据三角形外角的性质以及角平分线性质，可得∠ACE=2∠D+∠ABC，∠ACE=∠A+∠ABC，即可得∠A和∠D的数量关系．试题解析：解：（1）∵∠ABC＝60°，∠ACB＝40°，∴∠A＝80°．∵BD平分∠ABC，∠ABC＝60°，∴∠DBC＝30°．又∵∠ACB＝40°，∴∠ACE＝140°．又∵CD是∠ACE的平分线，∴∠DCE＝70°．∴∠D＝40°（2）∠A=2∠D．证明：∵CD 平分∠ACE∴∠ACE=2∠DCE又∠DCE=∠D+∠DBC∴2∠DCE=2∠D+2∠DBC∵BD平分∠ABC∴∠ABC=2∠DBC即∠ACE=2∠D+∠ABC而∠ACE=∠A+∠ABC∴2∠D=∠A【考点】三角形内角和定理;角平分线的性质;三角形外角的性质．13.如图，点B、C在∠SAT的两边上，且AB＝AC．（1）请按下列语句用尺规画出图形．（不写画法，保留作图痕迹）①AN⊥BC，垂足为N；②∠SBC的平分线交AN延长线于点M；③连接CM．（2）该图中有_______对全等三角形．【答案】详见解析．【解析】（1）作出∠SAT的角平分线，交BC于点N，根据等腰三角形三线合一的性质即可得AN⊥BC，根据角平分线的作法作出∠SBC的平分线交AN延长线于点M，连接CM即可．（2）图中有3对全等三角形，是△ABM≌△ACM，△ABN≌△ACN，△BMN≌△CMN．试题解析：（1）画图如下：（2）3【考点】角平分线的作法；等腰三角形的性质；全等三角形的判定．14.化简、求值：，其中，．【答案】，．【解析】先用整式乘法法则化简，然后把x，y的值代入即可．试题解析：原式===；当，时，原式==．【考点】整式的混合运算—化简求值．15.已知：如图，在Rt△ABC和Rt△BAD中，AB为斜边，AC=BD，BC，AD相交于点E．请说明AE=BE的理由【答案】详见解析．【解析】根据已知条件，利用HL可以判定Rt△ACE≌Rt△BDE，根据全等三角形的性质可得AE=BE．试题解析：在Rt△ACE和Rt△BDE中，AB=BA，AC=BD，∴Rt△ACE≌Rt△BDE，∴AE=BE．【考点】全等三角形的判定和性质．16.（2013•衢州）“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．（1）求a的值．（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？【答案】（1）a=10；（2）检票到第20分钟时，候车室排队等候检票的旅客有260人．（3）至少需要同时开放5个检票口．【解析】（1）根据原有的人数﹣a分钟检票额人数+a分钟增加的人数=520建立方程求出其解就可以；（2）设当10≤x≤30时，y与x之间的函数关系式为y=kx+b，由待定系数法求出函数的解析式，再将x=20代入解析式就可以求出结论；（3）设需同时开放n个检票口，根据原来的人数+15分进站人数≤n个检票口15分钟检票人数建立不等式，求出其解即可．解：（1）由图象知，640+16a﹣2×14a=520，∴a=10；（2）设当10≤x≤30时，y与x之间的函数关系式为y=kx+b，由题意，得，解得：，y=﹣26x+780，当x=20时，y=260，即检票到第20分钟时，候车室排队等候检票的旅客有260人．（3）设需同时开放n个检票口，则由题意知14n×15≥640+16×15解得：n≥4，∵n为整数，∴n=5．最小答：至少需要同时开放5个检票口．【考点】一次函数的应用．17.（2015秋•宁远县期末）某校为了奖励在数学竞赛中获奖的学生，买了若干本课外读物准备奖励给他们，如果每人奖4本，则剩余8本；如果每人奖5本，则最后一人得到了课外读物但不足3本．设该校买了本课外读物，有x名学生获奖．（1）用含x的代数式表示y；（2）求出该校的获奖人数及所买课外读物的本数．【答案】（1）y=4x+8；（2）该校有11人获奖，所买课外读物是52本．或者该校有12人获奖，所买课外读物是56本．【解析】（1）根据每人奖4本，则剩余8本，即本书比学生数的4倍多8，据此即可写出关系式；（2）如果每人奖5本，则最后一人得到了课外读物但不足3本，即最后一人的本书大于0且小于3，据此求得x的范围，再根据x是正整数求解．解：（1）y=4x+8（2）根据题意，得，解不等式组，得10＜x＜13；因为x取正整数，所以x=11或x=12；当x=11时，y=4x+8=52；当x=12时，y=4x+8=56；所以该校有11人获奖，所买课外读物是52本．或者该校有12人获奖，所买课外读物是56本．【考点】一元一次不等式组的应用．18.如图，△ABC和△FPQ均是等边三角形，点D、E、F分别是△ABC三边的中点，点P在AB边上，连接EF、QE．若AB=6，PB=1，则QE= ．【答案】2【解析】连结FD，根据等边三角形的性质由△ABC为等边三角形得到AC=AB=6，∠A=60°，再根据点D、E、F分别是等边△ABC三边的中点，则AD=BD=AF=3，DP=2，EF为△ABC的中位线，于是可判断△ADF为等边三角形，得到∠FDA=60°，利用三角形中位线的性质得EF∥AB，EF=AB=3，根据平行线性质得∠1+∠3=60°；又由于△PQF为等边三角形，则∠2+∠3=60°，FP=FQ，所以∠1=∠2，然后根据“SAS”判断△FDP≌△FEQ，所以DP=QE=2．19.某业主贷款2．2万元购进一台机器，生产某种产品。
2022年SAT数学考试大纲一、整体概述2022年SAT数学考试大纲针对考生在数学领域的基础知识和解题能力进行综合评估。
本次考试旨在测试考生的数学概念理解、数学问题求解以及数学模型应用能力。
在整个考试过程中，考生将面对多个题型，包括选择题、填空题以及解答题。
以下将逐一介绍这些题型以及考试涉及的具体内容。
二、选择题选择题是SAT数学考试中的常见题型之一。
在该题型中，考生需要在给出的选项中选出正确答案。
本题型考察考生的数学概念理解和基础运算能力。
1. 几何与测量本部分主要考察几何图形、空间关系和测量等内容。
具体包括点、线、面、体的性质及其运算、平面几何基本定理、三角学等。
2. 数据分析和应用本部分主要考察数据分析和统计应用。
具体包括代数中的数据处理、概率与统计等。
3. 代数本部分主要考察代数概念和代数计算。
具体包括线性方程、二次方程、函数、多项式、指数和对数等。
三、填空题填空题是SAT数学考试中的另一种常见题型。
考生需要根据题目描述在给定的空白处填入正确的答案。
本题型考察考生的逻辑思维和数学运算能力。
1. 几何与测量填空题中的几何与测量部分主要考察对几何图形的运算和性质的理解。
包括线段长度、角度计算、图形面积和体积等。
2. 数据分析和应用填空题中的数据分析和应用部分主要考察对数据处理和统计问题的解决能力。
考生需要灵活运用概率与统计等相关知识。
3. 代数填空题中的代数部分主要考察对代数概念和运算法则的理解。
包括线性方程、二次方程、函数、多项式等。
四、解答题解答题是SAT数学考试的一项重要内容，考生需要给出完整的解题过程和计算过程。
本题型考察考生的问题求解能力和应用能力。
1. 几何与测量解答题中的几何与测量部分主要考察对几何图形的运算和性质的理解。
考生需要给出详细的证明过程和推理。
2. 数据分析和应用解答题中的数据分析和应用部分主要考察对数据处理和统计问题的解决能力。
考生需要给出详细的思路和计算过程。
3. 代数解答题中的代数部分主要考察对代数概念和运算法则的理解。
SAT寻证题是SAT考试中一种常见的题型，主要考察考生寻找证据和推理的能力。
以下是一些关于SAT寻证题的解题技巧：
1.读懂问题和选项：在开始寻找证据之前，首先要读懂问题和选项，明确题目要求和考察点。
2.寻找关键信息：寻证题的答案通常隐藏在文章中，考生需要快速找到关键信息，这些信息可能是
一些数字、时间、地点、人物等。
3.推理和分析：在找到关键信息后，考生需要通过推理和分析来得出答案。
推理时要注意逻辑关系
和因果关系，分析时要综合考虑所有相关信息。
4.注意细节：寻证题往往涉及到文章的细节，考生需要仔细阅读文章并注意细节，以免遗漏重要信
息。
5.排除干扰项：有时文章中会出现一些与问题无关的信息或干扰项，考生需要保持清醒的头脑，排
除干扰项，找出正确的答案。
6.总结答案：在得出答案后，考生需要总结答案并确保答案简洁明了。
如果需要对答案进行解释或
推理，考生需要给出合理的解释和推理依据。
以上是关于SAT寻证题的解题技巧，希望对你有所帮助。
祝你考试顺利！。
sat 标准-概述说明以及解释1.引言1.1 概述概述部分的内容可以从以下角度展开：SAT（Scholastic Assessment Test，学术评估测试）是美国大学入学评估考试之一，由美国大学委员会（College Board）主办。
SAT考试的目的是评估学生在阅读、写作和数学方面的能力，以帮助大学招生机构衡量申请者的学术潜力和适应能力。
SAT考试的历史可以追溯到20世纪20年代，起初是作为美国军队招募测试的一部分。
后来，SAT逐渐发展成为美国高中生申请大学入学的标准考试。
如今，SAT考试在全球范围内都有广泛应用，许多国际学生也参加SAT考试申请美国大学。
SAT考试的结构包含阅读、写作和数学三个部分，其中包括阅读理解、语法和数学运算等各种题型。
SAT的题目设计旨在考察学生的批判性思维、分析能力和解决问题的能力，而非纯粹的记忆能力。
通过SAT考试，学生可以展示自己在学术方面的素养，为申请大学提供有力的证明。
随着时间的推移，SAT考试的内容和形式发生了一些变化。
最新的SAT考试在2016年进行了全面改革，强调更贴近实际应用和现实生活的考察内容，取消了原有的词汇填空题，增加了相关性更强的实践性文章阅读和数据解析题。
SAT考试的重要性不仅仅体现在大学申请阶段，它还可以帮助学生提升综合能力和学术素养。
通过备考SAT，学生需要进行大量的阅读、写作和数学练习，培养自己的批判性思维和解决问题的能力。
这些能力在学术和职业发展中都具有重要作用。
总之，SAT标准考试是一项重要的学术评估测试，旨在评估学生在阅读、写作和数学方面的能力。
通过SAT考试，学生可以展示自己的学术潜力和适应能力，为申请大学提供有力的证明。
此外，备考SAT也可以帮助学生提升综合能力和学术素养，对学生的学术和职业发展具有重要意义。
1.2 文章结构2. 正文2.1 第一个要点在本文结构中，正文部分将分为三个要点进行讨论。
这些要点将从不同的角度深入探讨SAT（Scholastic Assessment Test）标准的相关内容。
高考改革的成功案例国外经验与借鉴高考改革的成功案例：国外经验与借鉴随着社会进步和教育水平的提高，高考改革成为了各国教育界关注的焦点。
高考作为一种评价学生综合素质和能力的重要手段，不断面临着各种挑战。
因此，借鉴国外的高考改革经验，对于我国高考改革具有重要意义。
本文将从国外两个成功的高考改革案例中，探讨其经验和能够借鉴之处。
第一部分：美国SAT考试美国的高中生在升学方面，主要依赖SAT（Scholastic Assessment Test）考试的成绩。
SAT考试主要评估学生在阅读、写作和数学方面的能力。
与中国高考相比，SAT考试更加注重学生的整体素质和创造力。
对于中国高考改革的借鉴，我们可以从以下几个方面着手：首先，注重综合素质评价。
与中国高考以一次性考试成绩为评判标准不同的是，SAT考试注重学生多方面能力的综合评估。
除了卷面考试，SAT还包括个人陈述和推荐信等综合素质评价的内容。
其次，培养创造力和思维能力。
SAT考试注重学生的批判性思维和问题解决能力的培养，考察学生对实际问题的分析和解决能力。
这种考试方式能够更好地培养学生的创新和实践能力，对中国高考改革带来启示。
第二部分：德国高考德国的高考（Abitur）考试被认为是欧洲最公平、最全面的一种升学考试制度。
德国的高考改革可以为我国高考改革带来以下启示：首先，注重学生兴趣导向。
德国的高考注重学生的兴趣和潜能培养，注重学生个性的发展。
学生可以根据自己的兴趣和特长选择特定的学科进行深入学习，这样有助于提升学生的学习积极性和主动性。
其次，注重实践能力培养。
德国的高考注重学生实践能力的培养和实际操作能力的考察。
通过实践能力的培养，学生能够更好地适应社会的发展需求。
第三部分：国外高考改革的借鉴启示通过对美国SAT考试和德国高考的借鉴，我们可以得出一些对我国高考改革有启示意义的结论：首先，高考改革要注重学生的综合素质评价。
要突出学生的创新能力、实践能力和批判性思维等能力的培养和考察。
美国高考制度美国高考制度是指美国国内的高中学业水平考试和大学入学考试。
这些考试对于学生的学术能力和未来的学术进程起着至关重要的作用。
美国高考制度的特点是多样性和竞争性。
一、高中学业水平考试在美国，高中学业水平考试（High School Equivalency Exam，简称HSE）是在高中毕业后向没有获得正规学位的学生提供一种证明其学术能力的机会。
这些考试包括General Educational Development（GED）测试、High School Proficiency Exam （HSPE）和其他地方性的考试。
这些考试旨在衡量学生对基础学科（如数学、科学、阅读和写作）的理解和应用能力。
通常，学生通过HSE考试后能够获得与高中文凭相当的资格，从而有资格申请大学或职业培训课程。
二、SAT和ACT考试在美国，大学入学考试主要包括SAT（Scholastic Assessment Test）和ACT（American College Testing）两种考试。
这两种考试是衡量学生高中学术能力和准备大学课程的标准化考试。
大部分美国大学对学生的SAT或ACT成绩有要求，因此这两种考试对于学生申请大学至关重要。
1. SAT考试SAT考试是由College Board组织的一种全国性标准化考试。
它包括阅读、写作和数学三个部分，总分为1600分。
SAT考试的目的是测试学生的分析和解决问题的能力，以及对写作和语言的理解和运用能力。
学生可以多次参加SAT考试，大学会根据学生的最好成绩进行录取。
2. ACT考试ACT考试是由美国ACT公司组织的一种全国性标准化考试。
它包括英语、数学、阅读和科学四个部分，以及一个可选的写作部分。
ACT考试的总分为36分，各个部分的分数均为1至36之间。
ACT 考试侧重于测试学生的学科知识和解题能力，以及阅读和写作的能力。
像SAT考试一样，学生也可以多次参加ACT考试，大学会根据学生的最好成绩进行录取。
一种求解3-sat问题的新方法一、informationand ideas: the author's message （对文本信息的考察）包括以下题型：1文本细节的考查1）直接信息题（explicitmeaning），该类题型能够直接从文本中找到信息，题目中通常出现如下字眼"accordingto the passage," "states," "indicates,"等。
如：theauthors indicate that people value gift-giving because they feel it？2）暗含信息题（implicitmeaning），该类题型须要认知文本的暗含意思，题目中通常发生如下字眼"basedon the passage," "it can reasonably be inferred,""implies," 等。
例如：basedon the passage, the author's statement "" impliesthat？3）类比题（analogy），考察对文本内容特征的把握及应用，如"whichof the following situations is most analogous to the relationshipmentioned in line 5to 10?2文本论据的考查循证题（citingtextual evidence），要求为上一题的答案寻找论据或者为某个结论提供论据。
例如：whichchoice provides the best evidence for the answer to the previousquestion? （找寻上一题答案论据），或者inlines 46-50（"prosecutionssens"），whatis the most likely reason jordan draws adistinction between twotypes of "parties"? （为某个结论提供更多论据）循证题是对文本论据的考察，在每个篇章中会出现两题，共10题。
ACM主要算法介绍初期篇一、基本算法(1)枚举(poj1753, poj2965)(2)贪心(poj1328, poj2109, poj2586)(3)递归和分治法(4)递推(5)构造法(poj3295)(6)模拟法(poj1068, poj2632, poj1573, poj2993, poj2996)二、图算法(1)图的深度优先遍历和广度优先遍历(2)最短路径算法(dijkstra, bellman-ford, floyd, heap+dijkstra)(poj1860, poj3259, poj1062, poj2253, poj1125, poj2240)(3)最小生成树算法(prim, kruskal)(poj1789, poj2485, poj1258, poj3026)(4)拓扑排序(poj1094)(5)二分图的最大匹配(匈牙利算法)(poj3041, poj3020)(6)最大流的增广路算法(KM算法)(poj1459, poj3436)三、数据结构(1)串(poj1035, poj3080, poj1936)(2)排序(快排、归并排(与逆序数有关)、堆排)(poj2388, poj2299)(3)简单并查集的应用(4)哈希表和二分查找等高效查找法(数的Hash, 串的Hash)(poj3349, poj3274, POJ2151, poj1840, poj2002, poj2503)(5)哈夫曼树(poj3253)(6)堆(7)trie树(静态建树、动态建树)(poj2513)四、简单搜索(1)深度优先搜索(poj2488, poj3083, poj3009, poj1321, poj2251)(2)广度优先搜索(poj3278, poj1426, poj3126, poj3087, poj3414)(3)简单搜索技巧和剪枝(poj2531, poj1416, poj2676, 1129)五、动态规划(1)背包问题(poj1837, poj1276)(2)型如下表的简单DP(可参考lrj的书page149)：1.E[j]=opt{D+w(i,j)} (poj3267, poj1836, poj1260, poj2533)2.E[i,j]=opt{D[i-1,j]+xi,D[i,j-1]+yj,D[i-1][j-1]+zij} (最长公共子序列)(poj3176, poj1080, poj1159)3.C[i,j]=w[i,j]+opt{C[i,k-1]+C[k,j]} (最优二分检索树问题)六、数学(1)组合数学1.加法原理和乘法原理2.排列组合3.递推关系(poj3252, poj1850, poj1019, poj1942)(2)数论1.素数与整除问题2.进制位3.同余模运算(poj2635, poj3292, poj1845, poj2115)(3)计算方法1.二分法求解单调函数相关知识(poj3273, poj3258, poj1905, poj3122)七、计算几何学(1)几何公式(2)叉积和点积的运用(如线段相交的判定，点到线段的距离等)(poj2031, poj1039)(3)多边型的简单算法(求面积)和相关判定(点在多边型内，多边型是否相交)(poj1408, poj1584)(4)凸包(poj2187, poj1113)中级篇一、基本算法(1)C++的标准模版库的应用(poj3096, poj3007)(2)较为复杂的模拟题的训练(poj3393, poj1472, poj3371, poj1027,poj2706)二、图算法(1)差分约束系统的建立和求解(poj1201, poj2983)(2)最小费用最大流(poj2516, poj2195)(3)双连通分量(poj2942)(4)强连通分支及其缩点(poj2186)(5)图的割边和割点(poj3352)(6)最小割模型、网络流规约(poj3308)三、数据结构(1)线段树(poj2528, poj2828, poj2777, poj2886, poj2750)(2)静态二叉检索树(poj2482, poj2352)(3)树状树组(poj1195, poj3321)(4)RMQ(poj3264, poj3368)(5)并查集的高级应用(poj1703, 2492)(6)KMP算法(poj1961, poj2406)四、搜索(1)最优化剪枝和可行性剪枝(2)搜索的技巧和优化(poj3411, poj1724)(3)记忆化搜索(poj3373, poj1691)五、动态规划(1)较为复杂的动态规划(如动态规划解特别的施行商问题等)(poj1191, poj1054, poj3280, poj2029, poj2948, poj1925, poj3034)(2)记录状态的动态规划(poj3254, poj2411, poj1185)(3)树型动态规划(poj2057, poj1947, poj2486, poj3140)六、数学(1)组合数学1.容斥原理2.抽屉原理3.置换群与Polya定理(poj1286, poj2409, poj3270, poj1026)4.递推关系和母函数(2)数学1.高斯消元法(poj2947, poj1487, poj2065, poj1166, poj1222)2.概率问题(poj3071, poj3440)3.GCD、扩展的欧几里德(中国剩余定理)(poj3101)(3)计算方法1.0/1分数规划(poj2976)2.三分法求解单峰(单谷)的极值3.矩阵法(poj3150, poj3422, poj3070)4.迭代逼近(poj3301)(4)随机化算法(poj3318, poj2454)(5)杂题(poj1870, poj3296, poj3286, poj1095)七、计算几何学(1)坐标离散化(2)扫描线算法(例如求矩形的面积和周长，并常和线段树或堆一起使用)(poj1765, poj1177, poj1151, poj3277, poj2280, poj3004)(3)多边形的内核(半平面交)(poj3130, poj3335)(4)几何工具的综合应用(poj1819, poj1066, poj2043, poj3227, poj2165, poj3429)高级篇一、基本算法要求(1)代码快速写成，精简但不失风格(poj2525, poj1684, poj1421,poj1048, poj2050, poj3306)(2)保证正确性和高效性(poj3434)二、图算法(1)度限制最小生成树和第K最短路(poj1639)(2)最短路，最小生成树，二分图，最大流问题的相关理论(主要是模型建立和求解)(poj3155, poj2112, poj1966, poj3281, poj1087, poj2289, poj3216, poj2446)(3)最优比率生成树(poj2728)(4)最小树形图(poj3164)(5)次小生成树(6)无向图、有向图的最小环三、数据结构(1)trie图的建立和应用(poj2778)(2)LCA和RMQ问题(LCA(最近公共祖先问题)，有离线算法(并查集+dfs)和在线算法(RMQ+dfs))(poj1330)(3)双端队列和它的应用(维护一个单调的队列，常常在动态规划中起到优化状态转移的目的)(poj2823)(4)左偏树(可合并堆)(5)后缀树(非常有用的数据结构，也是赛区考题的热点)(poj3415,poj3294)四、搜索(1)较麻烦的搜索题目训练(poj1069, poj3322, poj1475, poj1924,poj2049, poj3426)(2)广搜的状态优化：利用M进制数存储状态、转化为串用hash表判重、按位压缩存储状态、双向广搜、A*算法(poj1768, poj1184, poj1872, poj1324, poj2046, poj1482)(3)深搜的优化：尽量用位运算、一定要加剪枝、函数参数尽可能少、层数不易过大、可以考虑双向搜索或者是轮换搜索、IDA*算法(poj3131, poj2870, poj2286)五、动态规划(1)需要用数据结构优化的动态规划(poj2754, poj3378, poj3017)(2)四边形不等式理论(3)较难的状态DP(poj3133)六、数学(1)组合数学1.MoBius反演(poj2888, poj2154)2.偏序关系理论(2)博奕论1.极大极小过程(poj3317, poj1085)2.Nim问题七、计算几何学(1)半平面求交(poj3384, poj2540)(2)可视图的建立(poj2966)(3)点集最小圆覆盖(4)对踵点(poj2079)八、综合题(poj3109, poj1478, poj1462, poj2729, poj2048, poj3336, poj3315, poj2148, poj1263)附录：POJ是“北京大学程序在线评测系统”（Peking University Online Judge）的缩写，是个提供编程题目的网站，兼容Pascal、C、C＋＋、Java、Fortran等多种语言。
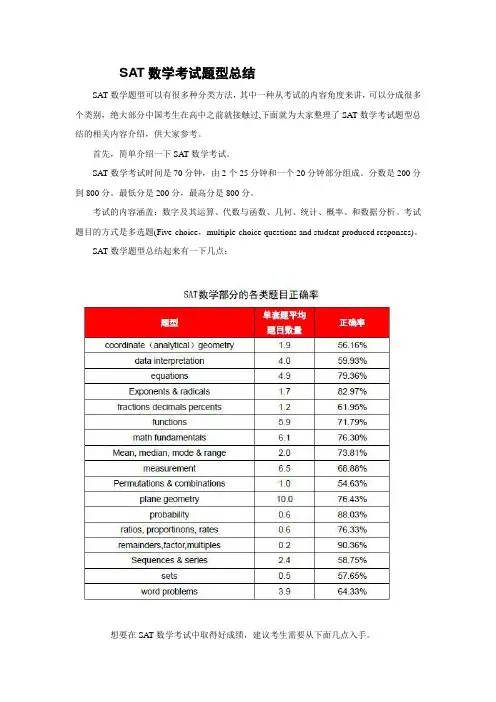
SAT数学考试题型总结
SAT数学题型可以有很多种分类方法，其中一种从考试的内容角度来讲，可以分成很多个类别，绝大部分中国考生在高中之前就接触过,下面就为大家整理了SAT数学考试题型总结的相关内容介绍，供大家参考。
首先，简单介绍一下SAT数学考试。
SAT数学考试时间是70分钟，由2个25分钟和一个20分钟部分组成。
分数是200分到800分。
最低分是200分，最高分是800分。
考试的内容涵盖：数字及其运算、代数与函数、几何、统计、概率、和数据分析。
考试题目的方式是多选题(Five-choice，multiple-choice questions and student-produced responses)。
SAT数学题型总结起来有一下几点：
想要在SAT数学考试中取得好成绩，建议考生需要从下面几点入手。
1、准备一个适合自己的复习计划：很多中国学生，由于轻视，都选择平时不做，考前随便做几套数学，背一遍单词，就去考的规划，然后SAT就会用710来回应这种轻视。
要根据自己的数学水平、细心程度等，给自己制定一个数学复习计划。
2、重视SAT数学单词。
3、准备SAT数学考试中的错题和难题。
从上面的关于SAT数学考试题型总结的分析我们就可以看到，SAT数学考试依然重视基础，大家在备考自己的SAT数学考试的时候，一定要根据自己的不同的基础决定不同的备考策略，对于各类SAT数学题型也要有针对性的练习才能更好的掌握。
1．苏瑞是小学三年级的学生，平时学习成绩不太好，但上课时特别爱举手回答问题。
有的时候，老师的问题还没有说完，他便把手高高举了起来，让他起来回答问题时，他又答不出来。
老师课下和苏瑞聊天，问原因，苏瑞说：“班上的同学总笑我成绩不好，说我笨，我不服气，所以老师提问时我总举手，是想向大家证明我不笨。
”老师了解了原委后，并没有批评苏瑞，而是和他定下君子协议：“以后老师提问时，如果真会回答，你举左手；如果不会，就举右手。
”在以后的课上，老师抓住苏瑞举左手的机会，让他回答问题，并经常地表扬他。
从那以后，苏瑞在学习上很有起色，不久就跨入了“先进生”的行列。
对案例中教师的教学行为进行评析。
答案：【参考答案】教师的本职是教书育人，案例中的老师从尊重学生入手，巧妙地采取“左右手”的方法，给苏瑞在班上表现自己的机会，既保护了苏瑞的自尊心，又提高了苏瑞的学习自信心和学习兴趣。
解析：【名师点睛】“为了每一位学生的发展”是素质教育的核心理念。
它要求教师要特别关注学生的个性，关注学生个性的差异，让每一位学生都有机会张扬自己的个性，展示自己的智慧与才华。
2、2．炎热的夏天，几个学生正站在树下，仰着头聚精会神地听着什么，一位老师远远地看见了，慢慢地走过去，轻声地问：“你们在干什么呢?”“听知了唱歌呢。
”学生头也不回，随口而答。
“知了唱什么歌呢?”老师又轻声地问道。
学生们回过神来，纷纷不好意思地低下头说：“不知道知了唱什么歌呢，就是觉得好听。
”老师笑着说：“知了是会唱歌，那你们知道知了是怎么唱歌的吗……”学生一边听，一边点头，并与老师进行讨论。
请你运用现代教育理论对该教师的行为进行评析。
答案：【参考答案】“听知了唱歌”说明学生具有童心、童真与童趣，具有儿童特有的想象力，是学生的一种体验，该教师的行为尊重和保护了孩子的兴趣和想象力；学生“在聚精会神地听”，处于其自身的活动过程，学生是能动的、发展的人，“教师轻轻地走过去”是尊重学生的主观能动性，保护学生，给学生以支持的表现；教师就“知了唱歌”展开科学教学，将学生的想象力加以引导，衍生到科学知识的学习上，使学生获得知识的同时，对其兴趣加以正确引导，真正做到素质教育。
1.正整数n有奇数个因子,则n为完全平方数2.因子个数求解公式:将整数n分解为质因子乘积形式,然后将每个质因子的幂分别加一相乘.n=a*a*a*b*b*c则因子个数=(3+1)(2+1)(1+1)eg. 200=2*2*2 * 5*5 因子个数=(3+1)(2+1)=12个3.能被8整除的数后三位的和能被8整除;能被9整除的数各位数的和能被9整除.能被3整除的数,各位的和能被3整除.4.多边形内角和=(n-2)x1805.菱形面积=1/2 x 对角线乘积6.欧拉公式：边数=面数+顶点数-28.三角形余玄定理C2=A2+B2-2ABCOSβ,β为AB两条线间的夹角9.正弦定理:A/SinA=B/SinB=C/SinC=2R(A,B,C是各边及所对应的角,R是三角形外接圆的半径)10.Y=k1X+B1,Y=k2X+B2，两线垂直的条件为K1K2=-111.N的阶乘公式:N!=1*2*3*....(N-2)*(N-1)*N 且规定0!=1 1!=1Eg:8!=1*2*3*4*5*6*7*812. 熟悉一下根号2、3、5的值sqrt(2)=1.414 sqrt(3)=1.732 sqrt(5)=2.23613. ...2/3 as many A as B: A=2/3*B...twice as many... A as B: A=2*B14. 华氏温度与摄氏温度的换算换算公式:(F-32)*5/9=CPS.常用计量单位的换算:（自己查查牛津大字典的附录吧）练习题:1：还有数列题：a1=2，a2=6，a n=a n-1/a n-2，求a150.解答: a n=a n-1/a n-2,所以a n-1=a n-2/a n-3,带入前式得a n=1/a n-3,然后再拆一遍得到a n=a n-6,也就是说,这个数列是以6为周期的,则a150=a144=...=a6,利用a1,a2可以=1/3.计算出a6如果实在想不到这个方法,可以写几项看看很快就会发现a150=a144,大胆推测该数列是以6为周期得,然后写出a1-a13(也就是写到你能看出来规律),不难发现a6=a12,a7=a13,然后那,稍微数数,就可以知道a150=a6了,同样计算得1/3.2：问摄氏升高30度华氏升高的度数与62比大小.key:F=30*9/5=54<623：那道费波拉契数列的题:已知,a1=1 a2=1 a n=a n-1+a n-2，问a1,a2,a3,a6四项的平均数和a1,a3,a4,a5四项的平均数大小比较。
解答:费波契那数列就是第三项是前两项的和,依此类推得到a1-a6为:1 123 5 8 13 21 a1+a2+a3+a6=12, a1+a3+a4+a5=11,所以为大于.4：满足x^2+y^2<=100的整数对（x,y）有多少？key: 按照X的可能情况顺序写出:X= Y=11-921-931-941-951-861-871-781-691-4 ＝>My answer:加起来=695：24，36，90，100四个数中,该数除以它的所有的质因子，最后的结果是质数的是那个：Key:906:0.123456789101112….，这个小数无限不循环地把所有整数都列出来.请问小数点后第100位的数字是多少？Key:位数0 1 2 3 4 5 6 7 8 9 1010 11 12 ………………………19 2020 21……………………………29 2030……………………………… 39 2040……………………………… 49 2050 51 52 53 54 55 56 ――――――第101位＝5？？7：2904x=y2（y的平方），x、y都是正整数，求x的最小值。
因为：X^2×Y^2×Z^2=(X×Y×Z)^2所以把2904除呀除＝2×2×2×3×11×11＝2^2×11^2×6再乘一个6就OK了 2^2×11^2×6×6＝（2×11×6）^2=132^2Key：最小的x＝68:序列An=1/n-1/(n+1),n>=1,问前100项和.解答：An ＝1/n-1/(n+1)An-1=1/(n-1)-1/nAn-2=1/(n-2)-/(n-1)………………………………………………A1＝1－1/2把左边加起来就是An +An-1+……+A1=1-1/(n+1) ...消掉了好多好多项之后的结果Key:把n＝100带入得前100项之和为100/1019:等腰三角形，腰为6.底边上的高为x,底边为y,问4x2+y2和144谁大解答:勾股定理得(y/2)2+x2=62,所以4x2+y2=14410:-1<r<t <0(有一数轴) question:r+r*t*t与-1的关系Key:我想的办法只能是尝试:原式=r(1+t*t)恒小于零1)r －1， t 0 则原式－12)r －1， t －1则原式－23)r 0 ， t 0 则原式 0例如：r＝-0.9 t=-1/3 时,原式=-1,若此时-0.9<t<-1/3 原式<-1 反之>-1.11:有长方形4feet*8feet,长宽各截去x inch,长宽比2：5，解答:列出方程:(4*12-x)/(8*12-x)=2/5=> x=161.排列(permutation):从N个东东(有区别)中不重复(即取完后不再取)取出M个并作排列,共有几种方法：P(M,N)=N!/(N-M)!例如:从1-5中取出3个数不重复,问能组成几个三位数？解答：P(3,5)=5!/(5-3)!=5!/2!=5*4*3*2*1/(2*1)=5*4*3=60也可以这样想从五个数中取出三个放三个固定位置那么第一个位置可以放五个数中任一一个,所以有5种可能选法，那么第二个位置余下四个数中任一个,....4.....，那么第三个位置……3……所以总共的排列为5*4*3=60同理可知如果可以重复选(即取完后可再取),总共的排列是5*5*5=1252．组合(combination):从N个东东(可以无区别)中不重复(即取完后不再取)取出M个(不作排列,即不管取得次序先后),共有几种方法C(M,N)=P(M,N)/P(M,M)=N!/(M-N)!/M!C(3,5)=P(3,5)/P(3,3)=5!/2!/3!=5*4*3/(1*2*3)=10可以这样理解：组合与排列的区别就在于取出的M个作不作排列-即M的全排列P(M,M)=M!，那末他们之间关系就有先做组合再作M的全排列就得到了排列所以C(M,N)*P(M,M)=P(M,N),由此可得组合公式性质:C(M,N)=C( (N-M), N )即C(3,5)=C( (5-2), 5 )=C(2,5) = 5!/3!/2!=103．概率概率的定义：P=满足某个条件的所有可能情况数量/所有可能情况数量概率的性质：0<=P<=11)不相容事件的概率：a,b为两两不相容的事件（即发生了a，就不会发生b)P(a或b)=P(a)+P(b)P(a且b)=P(a)+P(b)=0 (A,B不能同时发生)2）对立事件的概率:对立事件就是a+b就是全部情况,所以不是发生a,就是b发生,但是,有一点a,b 不能同时发生.例如:a:一件事不发生b:一件事发生,则A,B是对立事件显然：P（一件事发生的概率或一件事不发生的概率）=1（必然事件的概率为1）则一件事发生的概率=1 - 一件事不发生的概率...........公式1理解抽象的概率最好用集合的概念来讲，否则结合具体体好理解写a,b不是不相容事件(也就是说a,b有公共部分)分别用集合A和集合B来表示即集合A与集合B有交集，表示为A*B （a发生且b发生）集合A与集合B的并集，表示为A U B （a发生或b发生）则:P（A U B）= P(A)+P(B)-P(A*B).................公式23）条件概率：考虑的是事件A已发生的条件下事件B发生的概率定义：设A，B是两个事件，且P（A）>0,称P（B|A）=P（A*B）/P（A）....................公式3为事件A已发生的条件下事件B发生的概率理解：就是P（A与B的交集）/P（A集合）理解: “事件A已发生的条件下事件B发生的概率”，很明显，说这句话的时候，A，B都发生了，求的是A，B同时发生的情况占A发生时的比例，就是A与B同时发生与A发生的概率比。
4）独立事件与概率两个事件独立也就是说，A，B的发生与否互不影响，A是A，B是B，用公式表示就是P（A|B）=P(A)所以说两个事件同时发生的概率就是：P（A U B）＝P（A）×P（B）................公式4练习题:1：A, B独立事件，一个发生的概率是0.6 ，一个是0.8，问：两个中发生一个或都发生的概率？解答：P＝P(A且!B)+P(B且!A)+P(A且B)=0.6*(1-0.8)+0.8*(1-0.6)+0.6*0.8=0.92另一个角度,所求概率P=1-P(A,B都不发生)=1-(1-0.8)*(1-0.6)=0.922：一道概率题：就是100以内取两个数是6的整倍数的概率.解答:100以内的倍数有6,12,18,...96共计16个所以从中取出两个共有16*15种方法,从1-100中取出两个数的方法有99*100种,所以P=(16*15)/(99*100)=12/505=0.0243：1-350 inclusive 中，在100-299inclusive之间以3,4,5,6,7,8,9结尾的数的概率.因为100-299中以3,4,5,6,7,8,9结尾的数各有20个,所以Key:（2*10*7）/350=0.44.在1-350中（inclusive），337-350之间整数占的百分比Key:(359-337+1)/350=4%5.在E发生的情况下，F发生的概率为0.45，问E不发生的情况下，F发生的概率与0.55比大小解答:看了原来的答案,我差点要不考G了.无论柳大侠的推理还是那个哥哥的图,都太过分了吧?其实用全概率公式是很好解决这个问题的,还是先用白话文说一遍吧:某一个事件A的发生总是在一定的其它条件下如B,C,D发生的,也就是说A的概率其实就是在,B,C,D发生的条件下A发生的概率之和.A在B发生时有一个条件概率,在C发生时有一个条件概率,在D发生时有一个条件概率,如果B,C,D 包括了A发生的所有的条件.那么,A的概率不就是这几个条件概率之和么.P(A)=P(A|B)+P(A|C)+P(A|D)好了,看看这个题目就明白了.F发生时,E要么发生,要么不发生,OK?所以,P(F)=P(F|E)+P(F|!E) 感觉上也没错吧? 给了P(F|E)=0.45,所以P(F|!E)= P(F)-P(F|E)= P(F)-0.45如果P(F)=1,那么P(F|!E)=0.55如果0.45=<P(F)<1,那么0=<P(F|!E)<0.55如果…………，唉，我就不说你什么了…………sigh1.mode（众数）一堆数中出现频率最高的一个或几个数e.g. mode of 1,1,1,2,3,0,0,0,5 is 1 and 02.range（值域）一堆数中最大和最小数之差 ,所以统计学上又称之为极差.(两极的差)e.g. range of 1,1,2,3,5 is 5-1=43.mean（平均数）arithmatic mean（算术平均数）: n个数之和再除以ngeometric mean （几何平均数）: n个数之积的n次方根4.median（中数）将一堆数排序之后，正中间的一个数（奇数个数字），或者中间两个数的平均数（偶数个数字）e.g. median of 1,7,4,9,2,2,2,2,2,5,8 is 2median of 1,7,4,9,2,5 is (5+7)/2=65.standard error（标准偏差）一堆数中，每个数与平均数的差的绝对值之和，除以这堆数的个数(n) e.g. standard error of 0,2,5,7,6 is:(|0-4|+|2-4|+|5-4|+|7-4|+|6-4|)/5=2.46.standard variation一堆数中，每个数与平均数之差的平方之和，再除以n标准方差的公式：d2=[(a1-a)2+(a2-a)2+....+(an-a)2 ]/ne.g. standard variation of 0,2,5,7,6 is: average=4((0-4)2 +(2-4)2+(5-4)2+(7-4)2+(6-4)2)/5=6.87.standard deviation就是standard variation的平方根 d8.the calculation of quartile(四分位数的计算)Quartile（四分位数）：第0个Quartile实际为通常所说的最小值（MINimum）；第1个Quartile（En：1st Quartile）；第2个Quartile实际为通常所说的中分位数（中数、二分位分、中位数：Median）；第3个Quartile（En：3rd Quartile）；第4个Quartile实际为通常所说的最大值（MAXimum）；我想大家除了对1st、3rd Quartile不了解外，对其他几个统计值的求法都是比较熟悉的了，而求1st、3rd是比较麻烦的。
