多种类型地回归模型

基于系数平均的混合地理加权回归模型的估计及其系数类型辨识1.引言1.1 概述混合地理加权回归模型是一种用于解决空间分析和回归建模问题的重要方法。

它结合了地理加权回归模型和混合模型的优势，旨在提高回归模型的预测精度和解释能力。

该模型在广泛的领域中被广泛应用，包括城市规划、环境科学、社会经济学等。

地理加权回归模型是一种考虑了空间依赖性的回归建模方法。

它通过引入地理权重来反映不同地理位置样本之间的空间相关性，从而改善回归模型对空间异质性的建模能力。

然而，在某些情况下，地理加权回归模型的预测效果可能受到一些列影响因素的制约，如样本不平衡、非线性关系等。

为了克服这些限制，研究人员提出了系数平均的混合地理加权回归模型。

该模型在传统的地理加权回归模型的基础上，引入了系数平均的思想，通过对不同加权回归模型的系数进行平均，得到更稳健和准确的估计结果。

这种模型能够更好地应对数据的异质性，并提高预测模型的精度和解释能力。

本文旨在对基于系数平均的混合地理加权回归模型的估计方法及其系数类型辨识进行详细介绍。

在第2节中，我们将详细介绍该模型的建模方法和估计过程。

第3节将总结模型的实证结果，并对系数类型辨识的方法进行分析。

通过本文的研究，我们希望能够提供一个有效的分析工具和方法，为相关领域的研究者和决策者提供有益的参考和借鉴。

1.2文章结构1.2 文章结构本文将分为以下几个部分进行论述。

第一部分为引言部分。

在引言部分，首先对基于系数平均的混合地理加权回归模型进行概述，介绍其背景和意义。

接着，说明文章的结构和内容安排，并介绍本文的目的和意义。

第二部分为正文部分。

正文部分将详细讲解系数平均的混合地理加权回归模型及其估计方法。

首先，介绍混合地理加权回归模型的基本原理和假设条件。

然后，详细介绍系数平均的混合地理加权回归模型的构建方法和步骤。

接着，说明估计方法的选择和应用，包括参数估计和模型拟合等方面的内容。

最后，通过实例分析来验证该模型在实际问题中的应用价值和效果。

第三章地理加权回归模型介绍3.1 基本模型在地学空间分析中，n组观测数据通常是在n个不同地理位置上获取的样本数据，全局空间回归模型就是假定回归参数与样本数据的地理位置无关，或者说在整个空间研究区域内保持稳定一致，那么在n个不同地理位置上获取的样本数据，就等同于在同一地理位置上获取的n个样本数据，其回归模型与最小二乘法回归模型相同，采用最小二乘估计得到的回归参数户既是该点的最优无偏估计，也是研究区域内所有点上的最优无偏估计。

而在实际问题研究中我们经常发现回归参数在不同地理位置上往往表现为不同，也就是说回归参数随地理位置变化，这时如果仍然采用全局空间回归模型，得到的回归参数估计将是回归参数在整个研究区域内的平均值，不能反映回归参数的真实空间特征。

为了解决这一问题，国外有些学者提出了空间变参数回归模型（Spatially Varying-Coeffi Cient Regression Model）（Fosterand Gorr，1986；Gorrand Olligschlaeger，1994），将数据的空间结构嵌入回归模型中，使回归参数变成观测点地理位置的函数。

Fortheringham等（Brunsdonetal，1996；Fortheringham et al，1997；Brunsdon et al，1998）在空间变系数回归模型基础上利用局部光滑思想，提出了地理加权回归模型（Geographieally Weighted Regression Model-GWR）。

地理加权回归模型（GWR）是对普通线性回归模型（OLR）的扩展，将样点数据的地理位置嵌入到回归参数之中，即：式中：（u i，v i）为第i个样点的坐标（如经纬度）；βk（u i，v i）是第i个样点的第k个回归参数；i是第i个样点的随机误差。

为了表述方便，我们将上式简写为：若，则地理加权回归模型（GWR）就退变为普通线性回归模型（OLR）。

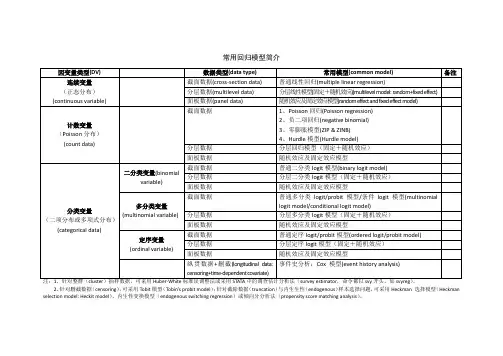
多因子回归模型
多因子回归模型是一种统计分析方法，可以通过分析多个变量之间的相关关系来推断模型的结果。

在经济研究中，多因子回归模型是经常用于分析股票市场、产品销量和全球经济因素等复杂行业的数据的统计模型。

多因子回归模型的基本形式用一个等式表示，其中Y是要预测的变量，多个因子X1至Xn（n≥2）代表该变量可能受到的其他因素影响，α和Β分别用于表征未知成分以及受影响因素之间的系数。

即：
Y = α + β1 * X1 + β2 * X2 + …… + βn * Xn
多因子回归模型包括三个组成部分：因变量Y，自变量X1到Xn以及未知系数β1到βn。

自变量X可以是定量变量或者定类变量，它可以表示各种可能影响Y的实际或潜在因素。

多因子回归模型的另一大优势在于它的易用性，它可以在任何可行的数据类型上实现，因而可以为复杂的经济问题提供有用的答案。

另外，它还可以通过确定各变量之间的相关性来检测复杂的模型结构，从而最大限度地提高模型的拟合精度。

总之，多因子回归模型是一种经常用于解决经济研究问题的有效分析方法，其能够精确地检测两个变量之间的相互影响及因素之间的系数，从而最大限度地提高模型的拟合精度。

多元回归分析及其应用多元回归分析是一种统计分析方法，可以用来研究多个自变量对一个因变量的影响关系。

相比于简单回归分析，多元回归分析考虑了更多因素的影响，能够更准确地描述变量之间的关系。

本文将介绍多元回归分析的基本原理和应用，以及如何进行该分析的步骤和解读结果。

一、多元回归分析的基本原理多元回归分析建立在线性回归的基础上，使用线性方程来描述因变量与自变量之间的关系。

它的基本模型可以表示为：Y = β0 + β1X1 + β2X2 + ... + βnXn + ε其中，Y表示因变量，X1、X2...Xn表示自变量，β0、β1...βn表示模型的系数，ε表示误差项。

多元回归分析的目标是通过拟合最佳的模型，得到各个自变量的系数，以及判断自变量对因变量的影响是否显著。

二、多元回归分析的步骤进行多元回归分析时，需要按照以下步骤进行：1. 数据收集与准备：收集与研究问题相关的数据，并进行数据清洗与整理，确保数据的准确性和完整性。

2. 模型设定：根据研究问题和数据特点，选择适当的模型。

根据自变量和因变量的关系类型，可以选择线性回归、多项式回归、对数回归等各种模型。

3. 模型拟合：使用统计软件进行多元回归分析，拟合出最佳模型。

统计软件会给出各个自变量的系数、截距项以及模型的可靠性指标。

4. 模型诊断：对模型进行诊断，检查模型的合理性和符合假设的程度。

可以通过观察残差图、相关系数矩阵、变量的显著性检验等方法来评估模型的质量。

5. 结果解读：根据模型的系数和统计指标，对结果进行解读。

判断自变量对因变量的影响是否显著，并分析各个自变量之间的相互影响。

三、多元回归分析的应用领域多元回归分析在各个学科和领域都有广泛的应用。

以下是其中几个具体领域的示例：1. 经济学：多元回归分析可以用来研究经济变量之间的关系，如GDP、失业率、通货膨胀率等。

2. 医学：多元回归分析可以帮助医学研究人员研究不同因素对疾病发展的影响，如药物剂量、生活方式等。

对多元线性回归模型的各种检验方法对于形如u X X X Y k k +++++=ββββΛΛ22110 （1）的回归模型，我们可能需要对其实施如下的检验中的一种或几种检验：一、 对单个总体参数的假设检验：t 检验在这种检验中，我们需要对模型中的某个（总体）参数是否满足虚拟假设0H ：j j a =β，做出具有统计意义（即带有一定的置信度）的检验，其中j a 为某个给定的已知数。

特别是，当j a =0时，称为参数的（狭义意义上的）显著性检验。

如果拒绝0H ，说明解释变量j X 对被解释变量Y 具有显著的线性影响，估计值j βˆ才敢使用；反之，说明解释变量j X 对被解释变量Y 不具有显著的线性影响，估计值j βˆ对我们就没有意义。

具体检验方法如下：（1） 给定虚拟假设 0H ：j j a =β；（2） 计算统计量 )ˆ(ˆ)ˆ()(ˆjj j j j j Se a Se E t βββββ-=-= 的数值； 11ˆ)ˆ(++-==j j jj jj j C C Se 1T X)(X ，其中σβ（3） 在给定的显著水平α下（α不能大于1.0即10%，也即我们不能在置信度小于90%以下的前提下做结论），查出双尾t （1--k n ）分布的临界值2/αt ；（4） 如果出现 2/αt t >的情况，检验结论为拒绝0H ；反之，无法拒绝0H 。

t 检验方法的关键是统计量 )ˆ(ˆj jj Se t βββ-=必须服从已知的t 分布函数。

什么情况或条件下才会这样呢？这需要我们建立的模型满足如下的条件（或假定）：（1） 随机抽样性。

我们有一个含n 次观测的随机样(){}n i Y X X X i ik i i ,,2,1:,,,,21ΛΛ=。

这保证了误差u 自身的随机性，即无自相关性，0))())(((=--j j i i u E u u E u Cov 。

（2） 条件期望值为0。

给定解释变量的任何值，误差u 的期望值为零。

广义回归模型一、概述广义回归模型是一种用于数据分析和建模的统计方法，它可以用来描述两个或多个变量之间的关系。

该模型可以通过最小化误差平方和来拟合数据，并根据数据中的变量来预测未知的结果。

广义回归模型是线性回归模型的扩展，它包含了其他类型的回归模型，如逻辑回归、泊松回归等。

二、线性回归模型1. 定义线性回归模型是一种广义回归模型，它假设因变量与自变量之间存在线性关系。

该模型可以用以下公式表示：Y = β0 + β1X1 + β2X2 + … + βpXp + ε其中，Y表示因变量，X1、X2、…、Xp表示自变量，β0、β1、β2、…、βp表示系数，ε表示误差项。

2. 最小二乘法最小二乘法是一种常用的拟合线性回归模型的方法。

该方法通过最小化残差平方和来确定最佳拟合直线。

3. 模型评估为了评估线性回归模型的拟合效果，可以使用以下指标：（1）R方值：R方值越接近1，则说明该模型对数据的拟合效果越好。

（2）均方误差（MSE）：MSE越小，则说明该模型对数据的预测效果越好。

三、逻辑回归模型1. 定义逻辑回归模型是一种广义线性回归模型，它用于建立因变量与自变量之间的非线性关系。

该模型可以用以下公式表示：P(Y=1|X) = e^(β0 + β1X1 + β2X2 + … + βpXp) / (1 + e^(β0 +β1X1 + β2X2 + … + βpXp))其中，P(Y=1|X)表示给定自变量时因变量为1的概率，e表示自然对数的底数，β0、β1、β2、…、βp表示系数。

2. 模型评估为了评估逻辑回归模型的拟合效果，可以使用以下指标：（1）准确率：准确率越高，则说明该模型对数据的拟合效果越好。

（2）召回率：召回率越高，则说明该模型对正样本的识别能力越强。

四、泊松回归模型1. 定义泊松回归模型是一种广义线性回归模型，它用于建立因变量与自变量之间的非线性关系。

该模型可以用以下公式表示：ln(μ) = β0 + β1X1 + β2X2 + … + βpXp其中，μ表示因变量的均值，β0、β1、β2、…、βp表示系数。

回归模型在统计分析中的应用目录1. 内容简述 (2)1.1 回归分析的定义和目的 (2)1.2 回归模型在统计分析中的重要性 (3)2. 回归模型的基础知识 (5)2.1 线性回归模型 (6)2.2 非线性回归模型 (8)2.3 回归模型的假设条件 (9)3. 回归模型的构建 (10)3.1 数据预处理 (11)3.2 模型选择与估计 (12)3.3 模型拟合与评估 (13)4. 具体应用 (15)4.1 金融领域 (16)4.1.1 股票价格预测 (17)4.1.2 信用评分模型 (19)4.2 健康研究 (20)4.2.1 疾病风险评估 (21)4.2.2 治疗效果分析 (22)4.3 经济分析 (23)4.3.1 经济增长预测 (24)4.3.2 消费行为研究 (25)4.4 营销管理 (26)4.4.1 消费者行为分析 (27)4.4.2 广告效果评估 (29)5. 模型优化和扩展 (30)6. 回归模型的解释和报告 (32)6.1 结果解释 (33)6.2 CFA表示法 (34)6.3 报告撰写技巧 (36)7. 回归分析软件工具 (37)8. 案例研究 (38)8.1 案例一 (40)8.2 案例二 (41)8.3 案例三 (42)9. 结论与展望 (43)9.1 回归模型在统计分析中的价值 (44)9.2 未来研究方向 (45)1. 内容简述回归模型在统计分析中扮演着至关重要的角色，它是一种强大的工具，用于探究自变量（解释变量）与因变量（响应变量）之间的关系。

通过构建和分析回归模型，我们可以对数据进行预测、估计和解释，从而为决策提供科学依据。

本文档将详细介绍回归模型的基本概念、类型、特点以及应用场景。

我们将从回归模型的基本原理出发，逐步深入探讨不同类型的回归模型，如线性回归、逻辑回归等，并针对每种模型提供实例数据和案例分析。

我们还将讨论回归模型的诊断与验证方法，以确保模型的准确性和可靠性。

多元非线性回归多元非线性回归分析是具有两个以上变量的非线性回归模型。

解决多元非线性回归模型的传统方法仍然是找到一种将其转换为标准线性多元回归模型的方法。

一些非线性回归模型可以通过适当的数学变换来获得其线性化表达式，但是对于其他非线性回归模型，仅变量变换没有帮助。

属于前一种情况的非线性回归模型通常称为内在线性回归，而后者称为内在非线性回归。

补充数据：线性回归线性回归是一种统计分析方法，在数学统计中使用回归分析来确定两个或多个变量之间的定量关系。

表达式形式为y = w'x + e，E为误差的正态分布，平均值为0。

在回归分析中，仅包含一个自变量和一个因变量，并且两者之间的关系可以近似地由一条直线表示。

这种回归分析称为单变量线性回归分析。

如果回归分析包括两个或多个自变量，并且因变量和自变量之间的关系是线性的，则称为多元线性回归分析。

在统计中，线性回归是一种回归分析，它使用称为线性回归方程的最小二乘函数对一个或多个自变量与因变量之间的关系进行建模。

此函数是一个或多个称为回归系数的模型参数的线性组合。

仅一个自变量的情况称为简单回归，而一个以上自变量的情况称为多重回归。

（这又应通过多个因变量而不是单个标量变量预测的多个线性回归来区分。

）在线性回归中，数据是通过线性预测函数建模的，未知模型参数是通过数据估算的。

这些模型称为线性模型。

最常用的线性回归建模是给定x值的Y的条件平均值是X的仿射函数。

在不太常见的情况下，线性回归模型可以是Y的条件分布的中位数或其他分位数像所有形式的回归分析一样，线性回归关注于给定x值的Y的条件概率分布，而不是X和Y的联合概率分布（在多元变量领域）分析）。

线性回归是经过严格研究并在实际应用中广泛使用的第一类回归分析。

这是因为与未知参数线性相关的模型比对位置参数非线性相关的模型更容易拟合，并且更容易确定结果估计的统计特征。

线性回归模型通常通过最小二乘近似进行拟合，但也可以通过其他方法进行拟合，例如最小化某些其他规范中的“拟合缺陷”（例如最小绝对误差回归）或最小化最小二乘的惩罚桥回归中的损失函数，最小二乘近似可用于拟合那些非线性模型。