下载文档原格式
空间直线与平面认识空间直线与平面的特征与方程空间直线与平面是几何学中重要的概念，它们在解决实际问题和研究几何性质中起着重要的作用。
本文将介绍空间直线与平面的特征与方程，并探讨它们在几何学中的应用。
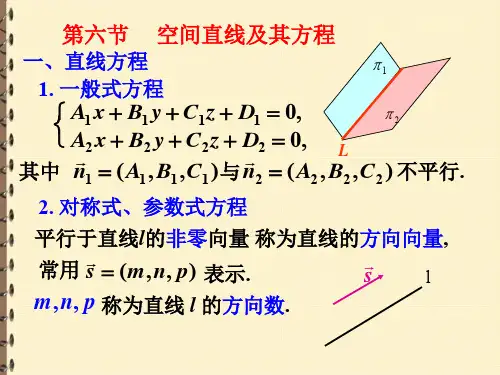
一、空间直线的特征与方程空间直线是由无穷多点组成的一条直线，它具有以下特征：1. 直线上的任意两点可以确定一个向量，这个向量称为方向向量。
方向向量可以用来描述直线在空间中的走向。
2. 直线上的一个点可以用坐标表示，直线上所有点的坐标可以用参数方程表示。
3. 直线可以与平面相交，也可以平行于某个平面。
空间直线的方程有多种表示方法，其中一种常用的方法是点向式方程。
设直线上一点为P(x0, y0, z0)，直线的方向向量为a，那么直线的点向式方程为：(x-x0)/a = (y-y0)/b = (z-z0)/c其中a，b，c分别为方向向量的三个分量。
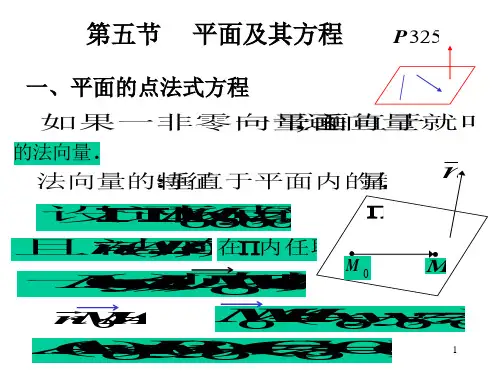
二、平面的特征与方程平面是由无穷多点组成的一个二维平面，它具有以下特征：1. 平面上的任意两点可以确定一个向量，这个向量称为法向量。
法向量垂直于平面，用来描述平面的朝向。
2. 平面上的一个点可以用坐标表示，平面上所有点的坐标可以用参数方程表示。
3. 平面可以与直线相交，也可以平行于某个直线。
平面的方程有多种表示方法，其中一种常用的方法是点法式方程。
设平面上一点为P(x0, y0, z0)，平面的法向量为n(x1, y1, z1)，那么平面的点法式方程为：n·(r-r0) = 0其中r(x, y, z)为平面上的任意一点坐标。
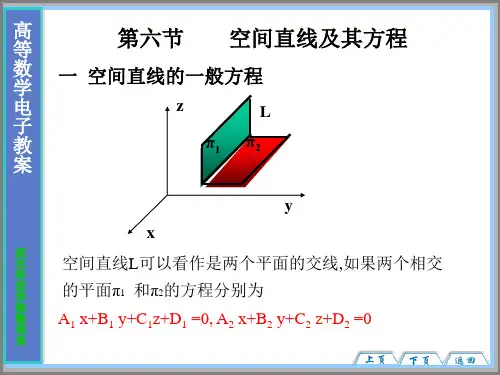
三、空间直线与平面的关系空间直线与平面之间有四种基本关系：1. 直线与平面相交，交点为直线上的一点。
2. 直线与平面平行，直线上的所有点都不在平面上。
3. 直线在平面内，直线上的所有点都在平面内。
4. 直线与平面重合，直线上的所有点都在平面上。
判断直线与平面之间的关系可以通过直线与平面的方程来进行。
四、空间直线与平面在几何学中的应用空间直线与平面在几何学中有广泛的应用，特别是在三维几何和立体图形的研究中。
空间直线的标准方程在三维空间中，直线是一种基本的几何图形，它具有许多重要的性质和应用。
本文将介绍空间直线的标准方程，以帮助读者更好地理解和运用直线的相关知识。
首先，我们来看一下空间直线的定义。
空间中的直线可以用两个不重合的点来确定，也可以用一个点和一个方向向量来确定。
如果我们已知直线上的一点P(x0, y0, z0)和一个与直线平行的向量a(a1, a2, a3)，那么直线上的任意一点Q(x, y, z)都可以表示为P 到Q的位移向量r与方向向量a的线性组合：r = PQ = (x x0, y y0, z z0)。
a = (a1, a2, a3)。
根据向量的性质，我们知道向量r与向量a平行，即它们的叉乘为零向量：r × a = 0。
展开叉乘运算，我们可以得到直线的标准方程：(x x0) / a1 = (y y0) / a2 = (z z0) / a3。
这就是空间直线的标准方程。
通过这个方程，我们可以方便地求解直线上的任意一点的坐标，也可以判断一个给定的点是否在直线上。
除了标准方程，我们还可以用参数方程和对称方程来表示空间直线。
参数方程是将直线上的任意一点表示为一个参数t的函数，而对称方程则是用直线上的一个固定点和一个方向向量来表示直线上的任意一点。
这些方程形式各有特点，可以根据具体的问题选择合适的表示方式。
在实际应用中，空间直线的标准方程可以帮助我们解决许多几何和物理问题。
比如，在计算机图形学中，我们常常需要判断一条射线是否与一个三维物体相交，这时就可以利用直线的标准方程来进行计算。
在工程设计中，直线的标准方程也可以用来描述物体的运动轨迹和空间布局。
总之，空间直线的标准方程是解决空间几何问题的重要工具，它具有简洁清晰的形式，可以方便地应用于各种实际问题中。
通过学习和掌握这一知识点，我们可以更好地理解和运用空间几何的相关知识，为解决实际问题提供有力的工具和方法。
希望本文的介绍能够帮助读者更好地理解空间直线的标准方程，也希望读者能够在实际问题中灵活运用这一知识点，为自己的学习和工作带来更多的收获和成就。
