当前位置：文档之家 › 第6章非线性振动-1讲解

第6章非线性振动-1讲解

  • 格式：ppt
  • 大小：716.00 KB
  • 文档页数：33

下载文档原格式

  / 33

合集下载

非线性振动

非线性振动


能够求出精确解的非线性系统极少，一般使用数值方法计算。采用近似计算的方法大部分是针对 弱非线性系统。对于强非线性系统，首先需要求出与之相近，而又精确可积的非线性系统精确解，然后 对精确非线性解进行摄动，所导出的微分方程仍然需要借助数值方法求解。
1. 线性振动一般解与典型非线性方程
0 x 0 有阻尼自由振动系统 x 20 x
取决于系统阻尼比与固有频率和激励频率的关系，有
arctan
2 / 0 2 1 2 / 0
1
稳态相应振幅与激励振幅的比值有
A2 B
1
2
2 / 0 2 / 0 2
2
(t ) cx (t ) kx(t ) F cos t kA cos t 对方程 mx
2 2 (t ) n 变形为 x(t ) 2n x x(t ) n A cos t
通解 X cos(t ) ， 表响应对激励的滞后：
通解 X1 为： x
2 0
v n x0 0

2 d
2
v n x0 e nt cos d t 0 ，瞬态响应，逐步衰减。 d
2
A cos nt ，且根据
n 1 n

2
非线性振动
u u (1 u ) 0 ，主要研究自激振动 Van der Pol 方程 u
2 2
实际可能，将谐波取到 3 倍频：(根据实际情况略去无用的高阶项，但求解会存在不少问题！)
x x An cos nt An n 2 2 cos nt
记录非线性的现象和原因，记录求解非线性问题的计算方法 很多问题不实际算，是不会发现问题的 陈小飞，2009-10-16 目 录
(振动理论课件)非线性振动概述

(振动理论课件)非线性振动概述

➢ 由于处理非线性振动问题的数学工具尚不完备，数 值方法起着非常重要甚至是不可替代的作用。数值 方法在非线性振动中的突出作用是发现新现象，这 已成为非线性振动现代发展的突出特点。
气象学家洛伦兹教授在科学上是敏锐的，他并没有在经典科学 中寻找问题的答案，而是另辟蹊径地解答现象背后的深层次的 科学问题。他认为天气的变化是一个庞大而又复杂的非线性动 力学系统，用传统的线性动力学模型是无法描述那些非周期性 和对初始条件的敏感依赖性。
在复杂系统中，常常存在着系统发生的临界点。用著名的耗散 结构理论的创始人普里高津的话来说，系统存在着分叉点和涨 落机制，任何一个从经典科学来看不足为奇的小小干扰，往往 会导致系统从稳定转向不稳定，或从不稳定趋向稳定
非线性世界的发现
非线性世界是由一位气象学家发现的。
➢千百年以来,关于明天是晴还是雨，人们都是通过对云彩的观 察凭借经验估计。科学家一直希望天气变化的预报，能像日月 食和潮汐那样可以预言。
➢20世纪60年代初，美国麻省理工学院著名气象学家洛伦兹 教授最早尝试用计算机模拟天气。这种尝试完全是凭借着一种 信念：自然是有规律的，规律是可以认识的。一旦人们掌握了 这种规律，知道了初始条件，就可以通过逻辑和数学必然性的 桥梁，模拟过去，预见未来。
➢ 而上述各种实际现象在现代工程技术中愈来愈 频 繁 地 出 现 。 早 在 1940 年 美 国 塔 可 马 (Tacoma)吊桥因风载引起振动而坍塌的事故 就是典型的非线性振动引起破坏的例子。
➢ 有必要发展非线性振动理论，研究对非线性系 统的分析和计算方法，解释各种非线性现象的 物理本质，以分析和解决工程技术中实际的非 线性振动问题。
非线性振动概述
➢几何方法—研究非线性振动的定性分析方法
❖ 传统的几何方法 在常微分方程定性理论的基础上，根据相轨迹的几何 性质判断微分方程解的性质。利用相平面内的奇点和 极限环作为平衡状态和孤立周期运动的几何表述。
振动理论讲义第6章 非线性系统

振动理论讲义第6章 非线性系统


如果忽略质量的变化，单自由度系统的运动方程的一般形式可以写为
,, 0
(6.2)
带有非线性特征的系统称为非线性系统，其运动称为非线性振动或者非线性响应。
叠加原理不适用于非线性系统。一般来讲，非线性振动不是简谐的，其频率随振幅改变。
非线性现象的一个重要类型是弹性恢复力与变形不成比例。
6-1
图 6.1 非线性弹性静态荷载-位移曲线
,
(l)
则有
或 根据椭圆积分表，有
/
(m)
/
,
(n)
其中， , 是第一类椭圆积分，
, sin
.
对比方程(m)和(n)， 可知
2 1,
因此，
因而方程(m)重新写为
21
,
sin 1 2
,
√
(6.13)
如果弹性性质偏离线性很小，可设 0. 由方程(6.13)可得方程(h), 对应于线性恢
复力的情况。
如果 及 很大，方程(j)的第一项可以忽略，在方程(6.13)中，1 → , 因此 的表
自由振动频率也将随振幅增加。实际上，该问题的非线性是由于大位移引起的几何非线 性，不是弦的非线性性质。
图 6.3
另一个几何非线性的例子是图 6.3 所示的单摆，重 ，长度 。单摆离开竖直位置的
夹角为 , 单摆关于轴 的回复力矩为 sinϕ，绕轴的转动方程为
sin 0
(d)
把质量的惯性矩
/ 代入，有
sin 0
运动方程为
其中,
sin 0 / . 与方程(6.9)和(6.10)对应的旋转振动的相应方程为
T
m
m
U
(6.15)
m m
(6.16)
非线性动力学

非线性动力学


t∈R
x∈ Rn
的解，则显然它是不仅是时间的函数，而且也是初值的函数，即解随着初值的改变而改变， 可以将解记为
φ(t, x0 )
当 x0 是 R n 中的某一点时，φ (t, x0 ) 代表了 1 条解轨线，而
{φ(t, x0 ) x0 ∈ D}
则代表了一族轨线。将φ看成是一个映射，即
φ : R× Rn → Rn
运动行为，它在物理上对应了这样的一个观点：在系统的最初阶段，系统由于外界的初始干 扰，将呈现相当复杂的运动形式，但随着时间的延续，运动将进入平稳状态，而这种平稳状 态体现了动态系统的本质结构。
微分方程解的最终形态通常有： (1) 平衡点 (2) 周期解 (3) 拟周期解 (4) 混沌解
6.4.1 平衡点
图 6-7 所示是 2 维线性系统的相轨线，坐标原点是系统的平衡点，图 6-7a、b 中的平衡 点是稳定的，称为稳定结点，图 6-7c 中的平衡点是不稳定的，称为鞍点。
图 6-7 2 维线性系统的相轨线
6.5.2 任意解的稳定性
设 x = ψ (t)是微分方程 x& = F(t, x)
第 6 章 非线性动力学
-0.5
-1
-1.5
0.5
1
1.5
图 6-2 例 1 相图
例2
如图 6-3 所示是微分方程
&y& + 0.2 y& + y = 0
在相平面 (x1, x2 ) ，
x1 = y
x2 = y&
上的轨线图，平衡点为 (0,0)，当 t → ∞ 时，解轨线趋于平衡点。
0.6 0.4 0.2
-0.6
-0.4
-0.2 -0.2
非线性振动现象的分析与控制

非线性振动现象的分析与控制

非线性振动现象的分析与控制引言：振动是物体在受到外界力的作用下产生的周期性运动。

在很多实际应用中，振动现象是无法避免的。

传统的振动理论常常以线性振动为研究对象，但在实际工程中，由于材料的非线性特性或者复杂的系统结构等因素的影响，一些系统的振动往往表现出非线性特征，这给振动控制带来了挑战。

本文将从非线性振动的基本原理、分析方法和控制策略等方面进行介绍。

1. 非线性振动的基本原理非线性振动的基本原理是指在振动系统中，系统的运动方程中存在非线性项。

非线性项可能来自于系统的非线性弹簧，非线性摩擦力以及非线性扰动等。

这些非线性项会使得系统的运动不再满足叠加原理，产生新的现象。

在非线性振动中，振幅的大小和振动频率之间存在复杂的关系，如倍频现象、相位共振等。

2. 分析非线性振动的方法为了分析非线性振动系统，常常需要采用数值模拟方法。

其中，一种常用的方法是时域分析，即通过求解系统的运动方程，得到系统的时域响应。

另一种方法是频域分析，即通过将时域信号转换到频域，分析系统的频谱特性。

此外，还可以通过相平面分析方法来研究非线性系统的稳定性、受激振动和共振现象等。

3. 非线性振动的控制策略在实际应用中，为了控制非线性振动系统，常常需要采取相应的控制策略。

其中，一种常见的方法是使用非线性控制器，通过引入非线性反馈来补偿系统的非线性特性。

另一种方法是使用自适应控制策略，根据系统的变化实时调整控制参数。

此外，还可以通过参数识别和模型预测控制等方法来实现对非线性振动的控制。

4. 实际应用中的非线性振动现象非线性振动现象在实际应用中普遍存在。

例如在建筑结构中，由于地震或风荷载等外力的作用，结构会发生非线性振动，给结构的安全性和稳定性带来威胁。

在机械系统中，由于轴承的非线性摩擦力或者悬挂系统的非线性特性，机械系统会出现非线性振动，影响其性能和寿命。

因此，对于非线性振动的分析和控制具有重要的理论和实际意义。

结论：非线性振动现象是实际工程中普遍存在的重要问题。

非线性振动

非线性振动

非线性振动期末作业任课老师：姓名：学号：专业：课程：非线性振动非线性振动的理论研究方法非线性振动是指恢复力与位移不成正比或阻尼力不与速度一次方成正比的系统的振动。

尽管线性振动理论早已相当完善，在工程上也已取得广泛和卓有成效的应用，但在实际问题中，总有一些用线性理论无法解释的现象。

一般说，线性模型只适用于小运动范围，超出这一范围，按线性问题处理就不仅在量上会引起较大误差，而且有时还会出现质上的差异，这就促使人们研究非线性振动。

通过理论分析对非线性振动进行研究是目前最有效最基本最直接的方式。

理论研究分析最主要的任务是通过理论的研究分析来揭示各类非线性系统振动的基本理论和主要特点。

非线性振动理论研究分析的最重要的数学工具就是微分方程。

学者们在微分方程发展过程中发现用初等函数表达方程解的可能性极为有限之后，出现了三个比较重要的方向。

其一是引入新的函数作为解的表达，并研究这些函数的性质和数值解。

非线性振动中有个别的问题就可以用这种方法来求解方程，例如摆的大幅振动解用椭圆函数表达。

然而这方面的例子是极为有限的。

这就说明只有极少数非线性微分方程能够求出方程的解，所以通常必须用近似的求解方法求出非线性微分方程的近似解，这就需要用到求解非线性微分方程的两个最基本的方法，这就是定性方法和定量方法。

定性理论不通过解的表达式来研究分析解的性质，比如利用几何法作出微分方程所定义的积分曲线，运用稳定性理论引入另外的函数中，通过它们去研究解的性质。

把常微分方程定性理论与非线性振动联系起来主要应归功于前苏联的Andronov等建立起来的学派。

这些学者们把定性理论用来解决电学和力学中出现的大量非线性振动问题。

定性理论在发展的过程中，一方面在理论上形成了许多讨论奇点、周期解、极限环的定理、判据等，一方面形成了一些实用的作图方法，例如等倾线法、Lienard法、点映射等。

求解非线性微分方程近似解的方法中定量分析的方法包括数值解法以及解析法。

非线性振动_绪论

非线性振动_绪论


0.4 非线性振动的主要研究问题
• (1) 确定平衡点及周期解；（系统响应） • (2) 研究平衡点及周期解的稳定性；（局部性态） • (3) 研究方程参数变化时，平衡点及周期解个数的变化及 形态（稳定性）变化，即分岔与混沌运动； • (4) 研究在一定初始条件下系统长期发展的结果。（解的 全局形态）
3非线性振动系统的共振曲线不同于线性振动系统存在跳跃和滞后现象非线性振动系统的共振曲线不同于线性振动系统存在跳跃和滞后现象4某些有阻尼的非线性振动系统会出现自激振动振幅不衰减某些有阻尼的非线性振动系统会出现自激振动振幅不衰减?线性系统中自由振动总是衰减的esinntxat??5强迫振动系统有超谐波响应和次谐波响应成分?简谐激振力作用下的非线性系统响应波形除了与激振力频率相同的谐波外还含有频率为激振频率的几分之一即频率为的次谐波响应及频率为激振频率的整数倍即频率为的超谐波响应nm为正整数?由于存在次谐波与超谐波振动非线性系统共振频率的数目将多于系统的自由度nm6多个简谐激振力作用下的组合振动?如激励为?响应中的频率含mnnm12为正整数ftft1122coscos和7存在频率俘获现象?在非线性振动系统中当系统以振动受到另一激励时系统可能以其中之一的频率振动即频率俘获128在一定条件会出现分叉现象与混沌运动duffing方程的倍周期分叉现象与混沌运动03非线性振动问题的研究方法????????????????????????????????????????????????????????????????????????????????????????等价线性化法谐波平衡法伽辽金法多尺度法渐进法平均法小参数法摄动法近似法解析法
6 闻邦椿等.非线性振动理论中的解析方法及工程应用. 东北大学出版社，2001年 7 刘延柱，陈立群.非线性振动.北京：高等教育出版社，2001年 8 陈予恕.非线性振动. 北京：高等教育出版社，2002年 9 闻邦椿等.工程非线性振动. 北京：科学出版社， 2007年
(振动理论课件)非线性振动概述

(振动理论课件)非线性振动概述

而线性常微分方程的数学理论已十分完善，因此将非 线性系统以线性系统代替是工程中常用的有效方法， 但仅限于一定的范围。 ➢ 至于什么属于线性振动问题，在未说明该系统预期工 作范围之前没有明确答复。因为系统中某些部件响应 与其激励之间的关系可能会依赖与其工作范围
非线性振动概述
➢ 当非线性因素较强时，用线性理论得出的结果 不仅误差过大，而且无法对自激振动、参数振 动、多频响应、超谐和亚谐共振、跳跃现象等 实际现象作出解释。
A
几何非线性
➢几何非线性—例2
单摆振动方程 gsin 0
l 这是一个非线性方程，对于小偏角，sin
可以得到足够精确的线性方程 g 0
l
可得单摆的固有振动周期为 T 2 l 与摆角无关，具有等时性
g
但是对于较大的偏角，必须考虑动非线性的影响。如果偏角并不 十分大，可以对sinθ展开成泰勒级数只取前两项，
非线性振动概述
➢几何方法—研究非线性振动的定性分析方法
❖ 传统的几何方法是利用相平面内的相轨迹作为对运动 过程的直观描述。
❖ 在常微分方程定性理论的基础上，根据相轨迹的几何 性质判断微分方程解的性质。利用相平面内的奇点和 极限环作为平衡状态和孤立周期运动的几何表述。
❖ 因此，关于奇点的类型和稳定性的研究，关于极限环 的存在性和稳定性的研究，以及稳定性随参数变化的 研究，是传统几何方法讨论的主要内容。
➢ 在工程问题中，稳态运动往往对应于机械系统的正常 工作状态。这种工作状态必须是稳定的，因为只有稳 定的运动才是可实现的运动。
非线性振动的定性分析方法
➢ 相平面法是最直观的定性分析方法，它只适用于单 自由度系统
➢ 相平面法利用相轨迹描绘系统的运动性态。相轨迹 的奇点和极限环分别对应于系统的平衡状态和周期 运动。
非线性振动1

非线性振动1

1 0 0 x 1 x 1 c o s k ( t t 0 ) x 2 s in k ( t t 0 ) k x k x 0 s in k ( t t ) x 0 c o s k ( t t ) 1 0 2 0 2
通解为:
式中 x , x 2 0是初扰动,由此得:
1 2 n
严格的稳定性概念由 A .M 李雅普诺夫给出: 定义1 如果任取 0 ( H , 无论如何小),对于任意给定的初时 刻 t 0 0 ,存在 ( t , ) 0 ,( 由 t 0 和 确定),任取初扰动 x 0,只要满 足 x ,对于一切 t t 0 有 X ( t ) 那么系统(1)的平衡就是稳定的.
故单摆运动在其平衡位置是稳定的. 另外，根据，定理2，不是渐近稳定的 定理3 (巴尓巴欣---克拉索夫斯基,1952)如果存在正定函数 ,它由(1)构成 的全导数是常负的,并且在全导数为零的集合 ,除原点外,不包含(1)的整 条轨线在内,则(1)的无扰动运动是渐近稳定的. 例如,证明对于有阻尼的下垂摆,平衡是渐近稳定的. 证明:扰动运动的微分方程是:
T 1 2
1 2 k 2 A 1 2
1
2
1 2

求得 a 1 1
1 2
k
2
0
,
A
1 4
(k )
2 2
根据定理1,只要 A
0 ,即 k
时,函数 V ( x1 , x 2 )是正定的.
n
对于扰动运动微分方程 x X ( x ) x R , (1) 以下假设函数V ( x ) 是单值连续的.V (0 ) 0 ,对x具有连续偏导数 (i=1,2…n)
非线性振动概述

非线性振动概述

非线性振动概述
一、关于非线性振动
1、什么是非线性振动： 指不能用线性微分方程所能描述的运动。
2、发生非线性振动的根本原因是：振动系统由于某种因素而处于非线性状态。
（1）内在的非线性因素
※ 例如振动系统由于振幅过大，而出现了非线性恢复力
例如单摆： 恢复力矩为
当 50 时
sin 1 3 1 5
2、参数振动： 漏摆，荡秋千等可作为参数振动的实例；而航天器液体燃料
自由面的振荡对飞行的影响则是当代科研的前沿；对圆柱容器中 的水面上、下铅直振动时所发生的参量振动既是古老的话题，（1831年法拉第研究过） 也是当今热极一时的“混沌”的一个例子。
4
0
A x
X 0/
/
例10－12 轻质弹簧下挂一个小盘，小盘
以小物体与盘相碰时为计时零点，以新平衡位置为原点，即当t=0时，x>0, v>0。 可知，与之对应的位相角在第四相象限，所以选（D）
6
例10－11 一质点在x轴上作简谐振动，振幅A＝4cm，周期 T＝2s，其平衡位置取作坐标原点。若t＝0时质点第一次通过x＝－2cm处且向X轴负 方向运动，则质点第二次通过x＝－2cm处的时刻为
F x, x2 v, v2
对以上所述的非线性因素中，只要出现其中一种，系统的振动就是非线性的。即使振 动系统本身是线性的（或说所有内在的非线性因素都可忽略），若受到外来的非线性策 动力的作用，其振动也是非线性的。
针对具体的非线性因素，系统的振动形式是完全不同的。 3、非线性系统的本质特点是：
3! 5!
M mgl sin mgl( 1 3 1 5)
6 120
弹簧振子，当振幅过大，亦出现非线性现恢复力，即
F k1x k2 x 2 k3 x3
大学物理非线性振动讲解

大学物理非线性振动讲解

f=1.15,相轨迹分布看似没有规律,反映了某种内在的结构特征;
f=1.35,相轨迹又呈现比较简单分布, 恢复单倍周期状态,但此 时单摆并非作来回振动,而是作单向的旋转;
f =1.45,单摆运动出现2倍的周期,作单向旋转;
f=1.47,单摆出现4倍的周期,作单向旋转; f=1.50, 又出现貌似无规则的运动,但比 f=1.15,时更为混乱.
说明鞍点是不稳定的平衡点，
因为与之相连的四条相轨迹中
两条指向它，两条背离它，而
附近相轨迹呈双曲线状．
Ep
o

d
dt
o

势能曲线、相图、鞍点
假定存在阻尼和驱动力，让摆作受迫振动．这样一来， 双曲点就成了敏感区．能量稍大，单摆就会越过势垒的 顶峰，跨到它的另一侧；能量稍小，则为势垒所阻，滑 回原来的一侧单摆向回摆动。
g 4 2 64 2
式中θm是最大角位移，即单摆振动的角摆幅。
当m 时，T→∞，T/T’随摆幅θm变化关系如图所示。
可见单摆的周期是一个向无
穷大发展的非线性变化。
T T
单摆线性振动的相图
d2 g sin
2
dt 2 L
1
两边积分得
( d
dt
)2
2
2

C1
即
(d dt)2
§8.3 非线性振动
一、非线性振动系统
由非线性微分方程所描述的振动，称其为非线性振动。
下面以单摆做自由振动为例进行分析
单摆的线性振动
d2
mL dt 2
mg sin
d 2
dt 2

g sin
L
将sinθ按泰勒级数展开可得

非线性振动.ppt


t 0 x 2 V (t, x1, x2, x3) 2 x 2
这里，a( x ) x 2 ,b( x ) 2 x 2 。
注意： 设 V(t, x) 是具有无穷小上界的正定函数，
即 a( x ) V (t, x) b( x )
则 V(t, x) 的变化范围如图（手绘图）。
e t x1
取正定函数
V
x12

e
t
x
2 2
[注：V x12 x22 x，2 V (t,0) 0]
求得：V. et x22 (2a(t) 1)
。 根据定理（1），如果对一切 t
t0
，有a(t)
1 2
，则无扰运动是稳定的
定义4 如果存在K类函数b(r) ，使得函数V (t, x)在区域 t 0, x h, (h H)内， 满足：V (t, x) b( x )，则函数 V (t, x)具有无穷小上界。
(1) V (t, x) a( x ), V (t,0) 0 （正定的）
(2)
.
V (t, x)

0,
(常负的)
则非驻定系统（1）的无扰运动是稳定的。
例
求单自由度系统，q..
a(t)
.
q
e
t
q

0
无扰运动 q 0的稳定条件
解：化成标准形式

.
x1

x2

.
x2

a(t ) x 2
解析方法： 摄动法（小参数法） 渐进法（KBM法） 谐波法 多重尺度法
（3）数值解法
摄动法（小参数法）
L-P方法的基本概念由天文学家A. Lindstedt于1883年提出，

机械振动第6章非线性振动


F (t ) f1 n cos(n t ) f 2 n sin(n t )
其中,
1 T /2 f1 n T / 2 F (t ) cos (n t ) d t T 1 T /2 f 2 n T / 2 F (t ) sin (n t ) d t T
n 1


2 T
d d ml 2 l mg sin F cos t dt dt
2
●一个复杂的非线性系统。其解更为复杂。
结论：对于一个非线性系统，在确定的初始条件 下，其解可能具有不可预测的随机性。
第5章 非线性振动
5. 3.1 非线性振动的近似解析方法
定性分析方法讨论振动系统在奇点（平衡位置） 附近的运动稳定性，它不需要求解系统的动力学微 分方程。但定性分析方法的研究对象主要限于自治 系统，而且不能定量地计算系统运动的时间历程，
第五章 非线性系统的振动
5.1 非线性振动概述
5.2 非线性振动问题的主要特点 5.3 非线性振动问题的研究方法 5.4 分叉与混沌的概念
王卫滨
5.1 非线性振动概述
不能用线性微分方程描述的振动称为非线性振动。恢复力与位移不成 正比或阻尼力不与速度一次方成正比的系统的振动。 工程技术与自然界中的振动问题及现象，绝大多数属于非线性的，线 性振动系统往往是对非线性系统进行性 恢复力
非线性 激振力
5.2 非线性振动问题的主要特点
• (1) 非线性振动系统的频率与系统响应的振幅和初始条件有关
线性振动系统的振动周期不随振幅大小而变化
(2) 对于非线性振动系统,叠加原理不适用
• 对于线性微分方程
• 对于非线性系统
d n x1 x2 d n x1 d n x2 n n dt dt dt n

非线性振动现象

非线性振动现象振动是物体围绕平衡位置做周期性的来回运动，它是自然界中普遍存在的现象。

在很多实际问题中，我们会遇到非线性振动现象，即振动系统不满足线性的回复力定律。

非线性振动现象在物理学、工程学以及生物学等领域都有广泛的应用和重要的研究价值。

一、什么是非线性振动现象非线性振动现象是指振动系统的受力律不满足线性回复力定律，即系统力与位移之间的关系不是线性的。

与线性振动相比，非线性振动显示出更加丰富的运动特性和行为。

非线性振动现象的出现主要归结为以下几个方面的原因：1.回复力律的非线性：通常线性振动系统受到的回复力与振动的位移成正比，但在某些情况下，回复力可能随着位移的增加而变化速率不等，导致非线性振动现象的出现。

2.系统参数的非线性：振动系统的参数非线性，如刚度、阻尼系数、质量等的变化，也会导致系统的振动特性发生变化。

3.外部扰动的非线性：外界对振动系统的扰动如果不规律、不可逆，也会导致系统出现非线性振动现象。

二、非线性振动的种类非线性振动现象的种类繁多，下面介绍几种常见的非线性振动现象：1.硬度非线性：当振动系统的回复力不仅与位移的大小有关，还与位移的变化率有关时，就会出现硬度非线性。

硬度非线性表现为振动系统的频率与振幅的关系非线性，通常存在频率间跳变、倍频和次谐波等特点。

2.阻尼非线性：振动系统受到非线性阻尼时，会出现振幅的跃变、突变等非线性现象。

3.非线性共振：当振动系统的频率接近系统的特征频率时，振幅会出现非线性的迅速增大，达到共振峰值。

4.受迫非线性振动：当振动系统受到非线性外力激励时，振幅和频率会发生非线性变化。

三、非线性振动的应用非线性振动现象在各个领域都有广泛的应用和研究价值：1.物理学：非线性振动现象的研究在物理学领域中有重要的地位。

例如，非线性振动现象的研究为材料的性能评估和电磁波的传播提供了重要依据。

2.工程学：非线性振动的研究对于工程结构的设计和优化至关重要。

例如，建筑结构和桥梁的振动特性分析需要考虑非线性振动的影响。

机械振动第6章非线性振动ppt课件

.
第5章 非线性振动 5. 3.1 非线性振动的近似解析方法
定性分析方法讨论振动系统在奇点（平衡位置） 附近的运动稳定性，它不需要求解系统的动力学微 分方程。但定性分析方法的研究对象主要限于自治 系统，而且不能定量地计算系统运动的时间历程， 不能获得系统的频率、振幅等基本参数。
只有极少的非线性系统能获得精确的解析解，因 此，对大多非线性系统只能采用近似解析的方法。近 似解析方法主要用于弱非线性系统。
发生非线性振动的原因：
1、内在的非线性因素
振动系统内部出现非线性回复力
单摆（或复摆） 的回复力矩
Mm(g l35)
3! 5!
振动系统的参量不能保持常数，
如漏摆、荡秋千。
自激振动 .
2、外在的非线性影响 非线性阻尼的影响 如 frk1vk2v2k3v3 策动力为位移或速度的非线性函数
如 F F (x ,x 2 ,x 3 ,v ,v 2 ,v 3 ) 线性振动与非线性振动的最大区别： 线性振动满足叠加原理 非线性振动不满足叠加原理
基本解(x0, x0)的领域内展开成泰勒级数:
x 02xF(t)
x ( t,) x 0 ( t)x 1 ( t)2x 2 ( t)
.
第5章 非线性振动 5. 3.2 非线性振动的数值分析方法
数值分析方法就是对非线性系统进行数值积分，在 时域内把响应的时间历程离散化，对每一时间步长内可 按线性系统来进行计算，并对每一步的结果进行修正。 这种方法又称为逐步积分法或直接积分法。
步长D t 内的线性方程来求解，常用的数值分析方法有纽马克
（Newmark）法、威尔逊（Wilson） 法、Runge－Kutta法等。
纽马克（Newmark）法
梯形法 最早由欧拉提出，其基本思想是将方程的解，即位移响

振动理论06(1-2)-非线性振动

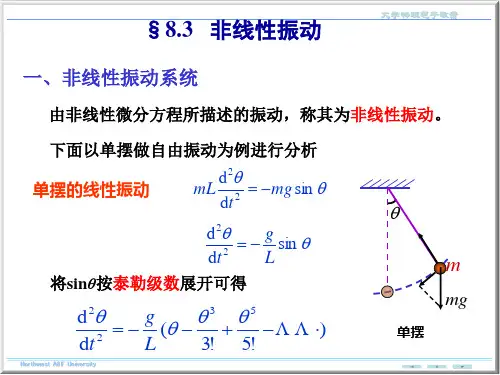
振动理论(6-1)第6章具有非线性特征的系统陈永强北京大学力学系6.1 非线性系统的举例●在粘性阻尼条件下，系统的运动微分方程为线性二阶常微分方程⏹线性振动理论能表征很多实际问题⏹对于不能用常系数线性微分方程来描述的物理系统，需要讨论非线性微分方程●忽略质量变化，单自由度系统的运动方程的一般形式可以写为⏹带有非线性特征的系统称为非线性系统，其运动称为非线性振动或者非线性响应⏹叠加原理不适用于非线性系统⏹通常，非线性振动不是简谐的，其频率随振幅改变非线性现象的一个重要类型是弹性恢复力与变形不成比例硬化弹簧软化弹簧32014/11/14质量附在长度为的拉直的弦AB 的中部，弦的初始张力用表示。

令质量在弦的横向上离开平衡位置的距离为，弦中产生的弹性恢复力如图(b )所示该系统自由振动方程：对称硬化弹簧的例子2014/11/144由几何关系代入运动方程显然这是一个非线性方程如果认为是小振动，有，因此52014/11/14●单摆，重，长度。

单摆离开竖直位置的夹角为, 单摆关于轴的回复力矩为，绕轴的转动方程为●代入质量的惯性矩, 有●小振幅情况为简谐振动，●振幅较大，对称软化弹簧的例子2014/11/14 6对比两种情况的非线性方程72014/11/14硬化情形分段线性化恢复力2014/11/148软化情形92014/11/14●如果动力荷载使结构或机器部件变形时超出了材料弹性范围，造成的运动称为非弹性响应●一建筑的二维矩形钢框架，受横向力作用于屋顶。

如果柱的弯曲刚度小于梁的弯曲刚度，随着荷载无限增加，在柱的两端会形成所谓的塑性铰。

102014/11/14●对应的载荷-位移曲线●实验表明，最大的正力和最大的负力在数值上是相等的●滞后回线关于原点对称2014/11/1411线性软化弹性卸载反向加载弹性卸载●曲线部分常常用直线代替，用以模拟真实的材料行为●双线性非弹性恢复力2014/11/1412双线性●理想弹塑性恢复力●滞后回线表示的能量耗散在这里被假定通过塑性铰损失掉，结构的其余部分依然保持能量守恒●这种能量耗散机制称为滞后阻尼2014/11/1413刚塑形带有摩擦抗力的单自由度系统及其滞后回线142014/11/14●下图两个问题在数学上是相同的⏹前者是属于刚塑形恢复力的情况，弹性变形与塑形范围相比很小⏹后者是没有弹簧的质量在摩擦力的阻滞下运动⏹除粘性阻尼外，其它类型的耗散机制均导致非线性⏹通常，假定质量、阻尼和刚度特征不随位移、速度和加速度而改变。

第6章非线性振动-1


鞍点
第6章 非线性振动
u 1 u 10 e l 1 t l t u 2 u 20 e 2
6. 2 非线性振动的定性分析方法
当 > 0，即两个特征值同号时，奇点为结点。当 两个特征值都为负时，当 t → ∞时，所有的轨线趋向于 原点，因此，奇点是稳定结点，系统的运动是渐近稳定 的。而当特征值同为正时，奇点是不稳定结点。

材料非线性 几何非线性 非线性阻尼 负刚度负阻尼
非线性特性
振幅过大超出材 料线弹性范围 位移或变形过大使结 构几何形状显著变化 材料内摩擦阻尼、流体 阻尼等都是非线性阻尼 有些情况下会存在 负刚度和负阻尼
第6章 非线性振动 非线性振动研究的内容
6.1 非线性振动概述
则有
l
1
l1
ln
u1 u 10

1
l
ln
2
u2 u 20
或
2
l1
ln
u1 u 10
ln
u2 u 20
设 = l 2 / l 1 ，则有 ln
ln u1

u1 u 10
ln
u2 u 20
或
u 10

ln
u2 u 20
第6章 非线性振动 从式 ln
u1

6. 2 非线性振动的定性分析方法 可得到相轨迹方程 u
设e1和e2是在原点的领域中小到可以忽略，则可以用
下列线性化方程讨论非线性方程在原点附近的稳定性：
x Ax
作非奇异线性变换
x B u
则方程可以写为
u Ju
其中
J B
1
AB
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

X 1 ( x1 , x2 ) a11 x1 a12 x2 e1 ( x1 , x2 ) X 2 ( x1 , x2 ) a21 x1 a22 x2 e 2 ( x1 , x2 )
叠加原理不成立
第6章 非线性振动
6. 2 非线性振动的定性分析方法
设n自由度系统的运动微分方程为
i (t ) fi (q1, q2 , ...; qn , q 1, q 2 , ..., q n ; t ) q
(i 1, 2, ..., n)
其中， qi是广义坐标，fi是广义坐标和广义速度的非线性函数。 位形空间 由变量qi规定的n维笛卡儿空间称为位形空间。方程的解qi(t) 可用位形空间的n维矢量表示。
非线性振动研究的基本内容之一就是建立对真实振动系统的计算方法， 改进计算精度，探索某些特殊现象的规律。
非线性振动的研究方法
非线性振动研究的方法有：定性分析、定量分析和数值分析方法。 定性法
研究已知解的领域内系统的一般稳定性特征，而不是运动的时 间历程。通常采用几何方法描述系统的运动特征。
定量法 通过一些渐近的解析方法研究系统运动的时间历程。 数值法 通过数值计算方法研究系统非线性振动的规律和现象。
相轨迹，或相迹。
不同初始条件的相轨迹组成相轨迹族。
第6章 非线性振动
6. 2 非线性振动的定性分析方法
奇点
相平面内能使状态方程右端等于零的特殊点称为相 轨迹的奇点。表明系统的速度和加速度均等于零，奇点 的物理意义即系统的平衡状态，因此也可将奇点称为平 衡点。 对单自由度自治系统的自由振动，状态方程为：

材料非线性 几何非线性 非线性阻尼 负刚度负阻尼
非线性特性
振幅过大超出材 料线弹性范围 位移或变形过大使结 构几何形状显著变化 材料内摩擦阻尼、流体 阻尼等都是非线性阻尼 有些情况下会存在 负刚度和负阻尼
第6章 非线性振动 非线性振动研究的内容
6.1 非线性振动概述
设由 xi 规定的相空间的原点与平衡点重合，则系统的运 动幅度定义为原点到扰动解积分曲线上任何一点的距离：
1 T 2 2 x ({ x} {x}) xi i 1
2n
1 2
Lyapunov稳定性定义
渐近稳定
不稳定
若给定任意小的正数e，存在正数 d，对于一切受扰运动，只要其初始扰 动满足 x(t0 ) d，对于所有的 t t 0 均满足 x(t ) e ，则称平凡解是稳定 的。
从状态方程可以看出平衡点的速度与加速度为零。 未扰解和被扰解 xi= fi (t )为方程的一个已知解，称为未扰解。研究系统 在fi (t )领域中的运动xi (t )称为被扰运动。 特别有意义的两类未扰解是对应于平衡点的常数解和对 应于封闭轨线的周期解。
i 1
第6章 非线性振动
6. 2 非线性振动的定性分析方法
第6章 非线性振动 自治系统和非自治系统
6. 2 非线性振动的定性分析方法
Xi中没有一个显含时间t 时，系统称为自治系统， Xi中至 少有一个显含时间t 时，系统称为非自治系统。 普通点和奇异点
T 2 凡是{ X } { X } X i 0的点称为普通点、相点或正则 2n
点；而{X} ＝{ 0 }的点称为奇异点或平衡点。
1 X 1 ( x1 , x2 ) x 2 X 2 ( x1 , x2 ) x
相平面
对于单自由度系统，相空 间缩减为以x1和x2为直角坐标 系的（x1，x2 ）平面，称为系 统线性振动的定性分析方法
相轨迹
与系统的运动状态 一一对应的相平面上的 点称为系统的相点。 系统的运动过程可用相 点在相平面上的移动过程来 描述。相点移动的轨迹称为
振动理论及其应用
第6章 非线性振动
6.1 非线性振动概述
6.2 非线性振动的定性分析方法 6.3 非线性振动的近似解析方法 6.4 非线性振动的数值分析方法 6.5 分叉与混沌的概念
第6章 非线性振动
6.1 非线性振动概述
非线性系统
当真实系统弹性元件的力与位移之间的关系超出线性范围，或阻尼元 件的力与运动速度之间的关系不满足作线性关系时，系统的运动微分方程不 能用线性微分方程描述，称系统为非线性系统。当真实系统作小运动时，可 忽略系统的高阶微小量，近似地将系统看作线性系统。
} { X } i (t ) X i ( x1 , x2 , ..., x2 n , t ) 或 {x 方程可写为 x
则矢量{x}可唯一表示系统在任一时刻t的状态。 相空间
i xn i 和 xn i X i，fi X n i q 设 qi xi ，
i规定的2n维空间称为状态空间或相空间。 由变量qi和 q
1 X 1 ( x1 , x2 ) x 2 X 2 ( x1 , x2 ) x
相平面上个别的平衡点就是以下方程的解：
X1 ( x1 , x2 ) 0, X 2 ( x1 , x2 ) 0
第6章 非线性振动
6. 2 非线性振动的定性分析方法
不失一般性，将坐标原点移至奇点处，并将函数在奇 点（0，0）附近展开为泰勒级数，得到：
第6章单 非线性振动 非线性振动与线性振动的区别 线性振动 自由振动频率与初始条件无关 强迫振动频率与激励力频率相 等 稳定平衡位置附近的运动是稳 定的 强迫振动中每个激励频率 有一个对应的振幅 叠加原理成立
6.1 非线性振动概述
非线性振动 自由振动频率与振幅有关 强迫振动频率成分复杂，有时 与激励频率不相等的频率成分 突出 稳定平衡位置附近具有多种 稳定和不稳定运动 强迫振动中幅频与相频曲线 发生弯曲，产生多值性
稳定
若这个平凡解是Lyapunov稳定的， 稳定性的几何解释 而且 lim x (t ) 0 ，则解是渐近稳定的。
t
第6章 非线性振动
6. 2 非线性振动的定性分析方法
讨论一单自由度自治系统的自由振动，其动力学方程 的一般形式为：
f (q, q ) q x2 和 x2 X1 ， f X 2 ，上式可以 设 q x1 ， q 写为状态变量的一阶微分方程组：