!!故障转子系统的非线性振动分析与诊断方法附录A matlab程序
- 格式:doc
- 大小:151.00 KB
- 文档页数:23

电梯曳引机在振动中的故障诊断分析摘要曳引机作为旋转机械是我国工业企业、日常生活中的常用设备-电梯中的关键部件,一旦发生事故就会严重影响整个设备甚至整个企业的正常运转。
本文首先探讨了电梯曳引机振动中的故障诊断的必要性与可行性,建立了电梯曳引机振动中的故障在线监测体系,并提出了相关发展展望。
关键词电梯曳引机;机械振动;故障诊断;在线监测中图分类号tu857 文献标识码a 文章编号1674-6708(2012)78-0065-01当前世界各国屡屡发生重大电梯安全事故,我国也曾发生多起断齿急坠事故,造成巨大经济损失[1-2]。
因此,开展电梯曳引机状态监测与故障诊断系统的研究意义重大。
本文为此具体探讨了电梯曳引机振动中的故障诊断体系的建立。
1 旋转机械振动中的故障诊断的必要性与可行性1.1 旋转机械振动中的故障诊断的必要性旋转机械故障诊断技术对于减少维修费用,降低生产成本,提高经济效益和社会效益具有重要作用。
一台200mw的汽轮机发电机每停机一天,则少发电480万千瓦时,经济损失高达数百万元[3],一台电梯停止运行,涉及千家万户的生活甚至安全。
可以通过监测机械设备是否出现故障的迹象来预知并防止可能产生的停机。
振动监测及机械设备诊断是对生产设备状态进行跟踪的有效方法,符合最佳维护实践,能够延长设备使用寿命,避免意外停机。
此外,访问关键生产设备运行状态的可靠性信息是至关重要的,而不是等到设备内部出现故障后得到一个故障信号。
机械设备停车保护只是整体监测策略的一部分,它针对的是那些不起眼的状况。
真正的监测设备需要训练有素的工作人员使用配套的软件在重要的压缩机、涡轮机、变速箱、泵、连接器和风机等设备发生意外故障前就发现和确定各种迹象。
不管如何,能够及时进行维护总要比等到发生灾难性的故障然后进行费用高昂的维修要好得多[4]。
1.2 旋转机械振动中的故障诊断的可行性某某企业通过对某电厂汽轮机的现场测试,分析了转子系统故障发生的原因,针对机器的振动超标问题,采取改变转子支承刚度和改变轴承支承位置等措施,保证了机器正常和可靠地运转,进而创造了近亿元的直接经济效益。
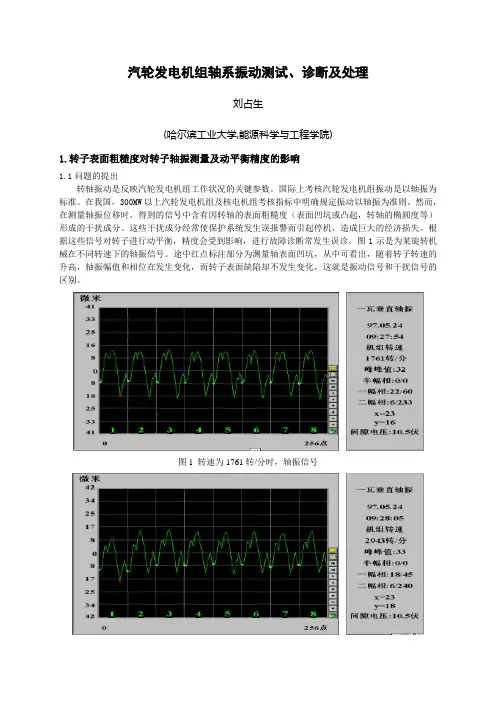
汽轮发电机组轴系振动测试、诊断及处理刘占生(哈尔滨工业大学,能源科学与工程学院)1.转子表面粗糙度对转子轴振测量及动平衡精度的影响1.1问题的提出转轴振动是反映汽轮发电机组工作状况的关键参数。
国际上考核汽轮发电机组振动是以轴振为标准。
在我国,300MW以上汽轮发电机组及核电机组考核指标中明确规定振动以轴振为准则。
然而,在测量轴振位移时,得到的信号中含有因转轴的表面粗糙度(表面凹坑或凸起,转轴的椭圆度等)形成的干扰成分。
这些干扰成分经常使保护系统发生误报警而引起停机,造成巨大的经济损失。
根据这些信号对转子进行动平衡,精度会受到影响,进行故障诊断常发生误诊。
图1示是为某旋转机械在不同转速下的轴振信号。
途中红点标注部分为测量轴表面凹坑,从中可看出,随着转子转速的升高,轴振幅值和相位在发生变化,而转子表面缺陷却不发生变化,这就是振动信号和干扰信号的区别。
图1 转速为1761转/分时,轴振信号图2 转速为2943转/分时,轴振信号图3 转速为3187转/分时,轴振信号图4 转速为3307转/分时,轴振信号1.2解决方法1.2.1低速补偿方法上述问题早已引起了人们的重视,美国Bently Navada公司转子动力学研究所曾提出了低速补偿的方法,但由于许多旋转机械(如,汽轮机发电机组)在不同负荷下,转子与静子间的胀差会发生变化,使传感器在不同转速、不同负荷下测量时所对的转轴位置不同,因此这种方法在测量时不仅未能消除干扰,反而引入了一个附加干扰。
因此,这种方法适用于转子与静子不发生轴向相对位移的场合。
1.2.2基于小波滤波方法根据振动信号的特点,将振动幅值变化大于某一设定值作为约束条件,采用小波方法滤掉转轴表面干扰成分,是当前采用的一种方法。
图5为转子在2089转/分时,光滑转子表面的轴振信号,视这组信号为真正的轴振信号。
然后,在传感器所对的径向平面内砸一个小坑,再将转子加速到2089转/分,测得的振动信号如图6所示。

转轴裂纹的故障机理与诊断石油化工行业的旋转机械一般转速都非常高,载荷也较大,长期运转后,转轴上易出现横向疲动裂纹,导致断轴的严重事故。
相对而言,转轴裂纹的故障概率比其他故障少得多,但因能产生轴裂纹的潜在原因很多,如各种因素造成的应力集中、复杂的受力状态、恶劣的工作条件和环境等,加之裂纹对振动响应不够敏感(深度达1/4直径的裂纹,轴刚度变化仅为10%左右,临界转速的变化也只有5%左右),有可能发展为断轴事故,危害极大。
因此,对轴裂纹诊断知识的学习很有必要。
一、故障机理转轴裂纹对振动的响应与裂纹所处的轴向位置、裂纹深度及受力情况有关。
视裂纹所处部位应力状态的不同,裂纹会呈现出三种不同的形态。
(1)闭裂纹转轴在压应力情况下旋转时,裂纹始终处于闭合状态。
例如,转子重量不大、不平衡离心力较小或不平衡力正好处于裂纹的对侧时就是这种情况。
闭裂纹对转轴振动影响不大,难以察觉。
(2)开裂纹当裂纹区处于拉应力状态时,轴裂纹始终处于张开状态。
开裂纹会造成轴刚度不对称,使振动带有非线性性质,伴有2×、3×、…等高频成分,随着裂纹的扩展,l×、2×、等频率的幅值也随之增大。
(3)开闭裂纹当裂纹区的应力是由自重或其他径向载荷产生时,轴每旋转一周,裂纹就会开闭一次,对振动的影响比较复杂。
理论分析表明,带有裂纹的转子的振动响应可分别按偏心及重力两种影响因素考虑,再作线性叠加。
由于偏心因素的影响,振动峰值会出现在与两个不对称刚度相应的临界转速之间;而重力因素的影响结果,是在转速约为无裂纹转轴的临界转速处时,会出现较大峰值。
裂纹的张开或闭合与裂纹的初始状态、偏心、重力的大小及涡动的速度有关,同时也与裂纹的深度有关。
若转子是同步涡动,裂纹会只保持一种状态,即张开或闭合,这与其初始态有关。
在非同步涡动时,裂纹在一定条件下也可能会一直保持张开或闭合状态,但通常情况下,转轴每旋转一周,裂纹都会有开有闭。

含故障滚动轴承-转子系统的非线性动力学分析含故障滚动轴承-转子系统的非线性动力学分析摘要:滚动轴承在转子系统中起着重要的支撑和传动作用。
然而,由于操作条件不良或材料疲劳等原因,滚动轴承可能出现故障,导致转子系统的性能下降甚至发生严重事故。
本文通过对含故障滚动轴承-转子系统的非线性动力学分析,探讨了故障对系统稳定性和振动响应的影响,并提出了相应的改进措施。
1. 引言滚动轴承是一种常见的机械传动元件,广泛应用于各种机械设备中。
在转子系统中,滚动轴承承担着支撑和传动的作用,对系统的性能和可靠性有着重要的影响。
然而,由于工作条件的变化和材料疲劳等原因,滚动轴承可能会出现故障,如疲劳裂纹、卡滞、磨损等,从而导致转子系统的性能下降。
2. 故障滚动轴承的动力学模型故障滚动轴承的动力学模型需要考虑轴承几何形状、材料特性和故障类型等因素。
在本文中,我们以单个滚动轴承为研究对象,将其建模为多自由度系统,考虑了转子和轴承的非线性特性。
3. 故障对转子系统稳定性的影响故障滚动轴承会引起转子系统的不稳定振动,影响系统的稳定性和可靠性。
通过分析系统的特征根和相平面图,可以得到故障滚动轴承的振动特性和稳定性边界。
4. 故障对转子系统振动响应的影响故障滚动轴承的存在将引起转子系统的非线性振动响应。
通过数值仿真和实验分析,可以研究故障滚动轴承对系统振动频谱、幅值和相位的影响。
5. 改进措施为了提高含故障滚动轴承-转子系统的稳定性和可靠性,可以采取以下改进措施:①改善润滑条件,减少摩擦和磨损;②使用可调节补偿机构,自动调整轴承间隙;③监测和检测系统的工作状态,及时发现和处理轴承故障。
6. 结论通过对含故障滚动轴承-转子系统的非线性动力学分析,可以得到故障对系统稳定性和振动响应的影响规律。
在实际应用中,我们应该重视滚动轴承的工作状态和健康监测,及时采取合理的预防和维护措施,以确保系统的安全稳定运行。
7.综上所述,故障滚动轴承对转子系统的稳定性和振动响应产生重要影响。

基于EEMD降噪和FFT的转子故障振动分析马转霞;费维科;周新涛;刘涛【摘要】针对转子产生故障时的振动信号受噪声干扰大、故障特征不明显这一难题,提出基于集合经验模式分解(EEMD)降噪和傅里叶变换(FFT)的转子振动信号分析方法.首先利用EEMD方法将原始故障信号分解成若干本征模态分量(IMF),然后计算各分量与原始信号之间的相关系数,筛选出有用分量并进行信号重构.最后对重构信号进行傅里叶变换(FFT)得到振动信号的特征频率.数值模拟和实验结果证明该方法的有效性和实用性.【期刊名称】《噪声与振动控制》【年(卷),期】2018(038)004【总页数】4页(P165-168)【关键词】振动与波;EEMD降噪;相关系数;FFT;故障特征【作者】马转霞;费维科;周新涛;刘涛【作者单位】西安汽车科技职业学院机械工程系,西安 710038;西安汽车科技职业学院机械工程系,西安 710038;西安汽车科技职业学院机械工程系,西安 710038;西安汽车科技职业学院机械工程系,西安 710038【正文语种】中文【中图分类】TH113.1;TN911.7转子是旋转机械的核心部件,其性能的好坏直接决定了系统工作的可靠性。
因此,必须定期监测转子的运行状况,一旦发生故障,系统应快速作出响应。
目前最常用的状态监测手段是通过振动信号分析来实现的。
但由于工作环境恶劣、测试条件有限等原因,所测得的振动信号往往夹杂了很多噪音干扰,大大降低了信号分析的准确性。
因此,故障诊断的第一步是减小或去除信号中的噪声干扰[1]。
经验模式分解(EMD)是一种适用于非线性、非平稳信号的处理方法,可将信号自适应地分为有限个本征模态分量(IMF),从中筛选出有用分量进行信号重构,从而达到降噪的效果。
但是,EMD算法在分解过程中容易出现频率混叠现象,严重影响降噪效果。
集合经验模式分解(EEMD)是EMD的改进算法,其原理是利用高斯白噪声频率的均匀性来消除分量之间频率的重叠和间断现象,使信号自适应地分解到不同尺度上,并保持连续,从而避免了模态混叠[2]。



旋转机械状态监测与故障诊断讲义陈国远深圳市创为实技术发展有限公司2005年8月目录第一章状态监测的基本知识 (4)一、有关的名词和术语 (4)1. 振动的基本参量:幅值、周期(频率)和相位 (4)2. 通频振动、选频振动、工频振动 (6)3. 径向振动、水平振动、垂直振动、轴向振动 (6)4. 同步振动、异步振动 (7)5. 谐波、次谐波、亚异步、超异步 (7)6. 相对轴振动、绝对轴振动、轴承座振动 (7)7. 自由振动、受迫振动、自激振动、随机振动 (7)8. 高点和重点 (8)9. 刚度、阻尼和临界阻尼 (8)10. 共振、临界转速、固有频率 (9)11. 分数谐波共振、高次谐波共振和参数激振 (9)12. 涡动、正进动和反进动 (9)13. 同相振动和反相振动 (10)14. 轴振型和节点 (10)15. 转子挠曲 (11)16. 电气偏差、机械偏差、晃度 (11)17. 偏心和轴心位置 (11)18. 间隙电压、油膜压力 (11)二、传感器的基本知识 (12)1. 振动传感器 (12)2. 电涡流振动位移传感器的工作原理 (13)3. 电动力式振动速度传感器的工作原理 (13)⒋压电式加速度传感器的工作原理 (14)第二章状态监测常用图谱 (15)1.波德图 (15)2.极坐标图 (16)3.频谱瀑布图 (16)4.极联图 (17)5.轴心位置图 (18)6.轴心轨迹图 (18)7.振动趋势图 (19)8.波形频谱图 (20)第三章旋转机械的故障诊断 (22)1. 不平衡 (22)2. 不对中 (23)3. 轴弯曲和热弯曲 (26)4. 油膜涡动和油膜振荡 (28)5. 蒸汽激振 (30)6. 机械松动 (33)7. 转子断叶片与脱落 (33)8. 摩擦 (38)9. 轴裂纹 (40)10. 旋转失速与喘振 (40)11. 机械偏差和电气偏差 (43)第一章状态监测的基本知识一、有关的名词和术语机械振动是指物体围绕其平衡位置附近来回摆动并随时间变化的一种运动。


双转子-中介轴承系统非线性振动特性高朋; 侯磊; 陈予恕【期刊名称】《《振动与冲击》》【年(卷),期】2019(038)015【总页数】10页(P1-10)【关键词】双转子; 中介轴承; 振动突跳; 双稳态; 非线性振动【作者】高朋; 侯磊; 陈予恕【作者单位】哈尔滨工业大学航天学院哈尔滨150001; 哈尔滨工业大学能源科学与工程学院哈尔滨150001【正文语种】中文【中图分类】V231.96采用双转子结构的航空发动机因具有较高的推重比和气动稳定性,不易发生喘振等优点,应用较为广泛。
但由于中介轴承的引入,使得航空发动机双转子系统振动耦合强烈、非线性突出[1]。
为理清双转子-中介轴承系统的动力学行为,从而提高航空发动机运行稳定性,国内外学者做了许多工作。
廖明夫等[2]建立了简支对称的双转子模型,运用解析方法研究了双转子的振动特性,并重点分析了中介轴承的影响,为转子结构设计和中介轴承选择提供了指导准则。
周海仑等[3-4]考虑了中介轴承的耦合作用、转静件的碰摩等,建立了双转子航空发动机整机动力学模型。
邓四二等[5]采用 Hertz 接触模型模拟中介轴承非线性力,采用 Newmark 法分析了转子转速及轴承参数对双转子系统动力学特性的影响,并进行实验验证。
胡清华等[6]建立了五自由度的航空发动机双转子模型,通过与三自由度模型和中介轴承线性化的五自由度模型对比,发现转子的旋转自由度和支撑的非线性对系统的动力学行为有很大影响。
罗贵火等[7-8]对比分析了同向和反向旋转双转子系统的拍振响应及轴心轨迹,并通过实验验证了理论结果。
Ferraris 等[9]分析了刚度阵非对称的反向旋转双转子的动力学特性,得到了临界转速、不平衡响应曲线以及进动方向的变化规律。
符毅强等[10]建立了考虑中介轴承非线性力的反向旋转双转子系统简化模型,通过数值求解发现系统的幅频响应存在明显的共振滞后现象,并分别讨论了转速比,中介轴承径向游隙以及阻尼比对系统滞后特性的影响。

转子动力学知识2转子动力学主要研究那些问题答:转子动力学是研究所有不旋转机械转子及其部件和结构有关的动力学特性,包括动态响应、振动、强度、疲劳、稳定性、可靠性、状态监测、故障诊断和控制的学科;这门学科研究的主要范围包括:转子系统的动力学建模与分析计算方法;转子系统的临界转速、振型不平衡响应;支承转子的各类轴承的动力学特性;转子系统的稳定性分析;转子平衡技术;转子系统的故障机理、动态特性、监测方法和诊断技术;密封动力学;转子系统的非线性振动、分叉与混沌;转子系统的电磁激励与机电耦联振动;转子系统动态响应测试与分析技术;转子系统振动与稳定性控制技术;转子系统的线性与非线性设计技术与方法;3转子动力学发展过程中的主要转折是什么答:第一篇有记载的有关转子动力学的文章是1869年Rankine发表的题为“论旋转轴的离心力”一文,这篇文章得出的“转轴只能在一阶临界转速以下稳定运转”的结论使转子的转速一直限制在一阶临界以下;最简单的转子模型是由一根两端刚支的无质量的轴和在其中部的圆盘组成的,这一今天仍在使用的被称作Jeffcott转子的模型最早是由Foppl在1895年提出的,之所以被称作“Jeffcott”转子是由于Jeffcott教授在1919年首先解释了这一模型的转子动力学特性;他指出在超临界运行时,转子会产生自动定心现象,因而可以稳定工作;这一结论使得旋转机械的功率和使用范围大大提高了,许多工作转速超过临界的涡轮机、压缩机和泵等对工业革命起了很大的作用;但是随之而来的一系列事故使人们发现转子在超临界运行达到某一转速时会出现强烈的自激振动并造成失稳;这种不稳定现象首先被Newkirk发现是油膜轴承造成的,仍而确定了稳定性在转子动力学分析中的重要地位;有关油膜轴承稳定性的两篇重要的总结是由Newkirk和Lund写出的,他们两人也是转子动力学研究的里程碑人物;4石化企业主要有哪些旋转机械,其基本工作原理是什么汽轮机:将蒸汽的热能转换成机械能的涡轮式机械;工作原理:在汽轮机中,蒸汽在喷嘴中发生膨胀,压力降低,速度增加,热能转变为动能;作用与功能:主要用作发电用的原动机,也可直接驱动各种泵、风机、压缩机和船舶螺旋桨等;还可以利用汽轮机的排汽或中间抽汽满足生产和生活的供热需要;燃气轮机:是一种以空气及燃气为介质,靠连续燃烧做功的旋转式热力发动机;主要结构由三部分:压气机,燃烧室,透平动力涡轮;作用与功能:以连续流动的气体为工作介质,带动叶轮高速旋转,将燃料的能量转变为有用功;工作原理:压气机即压缩机连续地仍大气中吸入空气幵将其压缩;压缩后的空气迚入燃烧室,不喷入的燃料混合后燃烧,成为高温燃气,随即流入燃气透平中膨胀做功,推动透平叶轮带着压气机叶轮一起旋转;加热后的高温燃气的做功能力显著提高,因而燃气透平在带动压气机的同时,尚有余功作为燃气轮机的输出机械功;压缩机:将机械能转变为气体的能量,用来给气体增压与输送气体的机械;作用与功能:将原动机的机械能转变为气体的能量,用来给气体增压与输送气体;工作原理:空气压缩机的种类很多,按照工作原理可分为容积式压缩机,往复式压缩机,离心式压缩机;容积式压缩机的工作原理是压缩气体的体积,使单位体积内的气体分子密度增加以提高压缩空气的压力;离心压缩机的工作原理是提高气体分子的运动速度,使气体分子具有的动能转化为气体的压力能,仍而提高压缩空气的压力;往复式压缩机也称活塞式压缩机的工作原理是直接压缩气体,当气体达到一定压力后排出;离心机:离心机是利用离心力,分离液体与固体颗粒或液体与液体混合物中各组分的机械;作用与功能:离心机主要用于将悬浮液中的固体颗粒与液体分开;或将乳浊液中两种密度不同,又互不相容的液体分开,它也可以用于排除湿固体中的液体;工作原理:有离心过滤和离心沉淀两种;离心过滤是使悬浮液在离心力场下产生的离心压力,作用在过滤介质上,使液体通过过滤介质成为滤液,而固体颗粒被截留在过滤介质表面,仍而实现液-固分离;离心沉降是利用悬浮液或乳浊液密度不同的各组分在离心力场中迅速沉降分层的原理,实现液-固或液-液分离;发电机:将其他形式的能源转换成电能的机械设备;作用与功能:由水轮机、汽轮机、柴油机或其他动力机械驱动,将水流,气流,燃料燃烧或原子核变产生的能量转化为机械能传给发电机,再由发电机转换为电能;工作原理:其工作原理都基于电磁感应定律和电磁力定律;由轴承及端盖将发电机的定子,转子连接组装起来,使转子能在定子中旋转,做切割磁力线运动,仍而产生感应电势,通过接线端子引出,接在回路中,便产生了电流;5什么是横向振动答:为了避开静变形,可以考虑转轴的两支点在同一垂直线上,而圆盘位于水平面如下图;圆盘以角速度Ω作等速转动;当正常运转时,转轴是直的;如果在它的一侧加一横向冲击,则因转轴有弹性而发生弯曲振动,或圆盘作横向振动;6什么是涡动进动,其频率是多少答:转轴在不平衡力矩作用下,发生挠曲变形,将产生两种运动,一是转轴绕其轴线的定轴转动,一种是形的轴线绕其静平衡位置的空间回转;两种运动的合成即是涡动;圆盘或转轴中心在相互垂直的两个方向作频率同为ωn 的简谐运动,一般情况下,两个方向上的振幅不相等,所以圆盘轴心轨迹为一椭圆,轴心的这种运动是一种涡动或进动;自然频率ωn 称为进动角频率;圆盘或转轴中心的进动或涡动属于自然振动,它的频率就是圆盘没有振动时,转轴弯曲振动的自然频率;7什么是自动对心答:当轴心的响应频率进大于圆盘偏心质量产生的激振力频率时,圆盘的重心近似地落在固定中心,振动很小,转动反而比较平稳;这种情况称为自动对心;8什么是临界转速答:转子在某些特定的转速下转动时会发生很大的变形并引起共振,引起共振时的转速;数值上等于转子固有频率的转速;9什么是刚性轴和柔性轴答:如果机器的工作转速小于临界转速,则转轴称为刚性轴;如果工作转速高于临界转速,则转轴称为柔性轴;10什么是幅频响应曲线和相频响应曲线答:振幅A 与位相差θ随转动角速度对固有频率Ω/ωn 的比值改变的曲线,即幅频响应曲线和相频响应曲线;11什么是陀螺效应产生陀螺力矩的基本条件是什么答:陀螺效应就是旋转的物体有保持其旋转方向旋转轴的方向的惯性;当圆盘不装在两支承的中点而偏于一边时,高速旋转的圆盘的自转轴也就是圆盘的动量矩被迫不断的改变方向,就会产生陀螺力矩,出现陀螺效应;只要高速旋转部件的自转轴在空间改变方向即进动,就会产生陀螺力矩,出现陀螺效应;12怎样计算考虑陀螺力矩时转子的临界角速度陀螺力矩对进动角速度数目和幅值的影响是什么答:1计算转子的临界转速时,需要列出圆盘的运动微分方程;求解这组齐次线性微分方程的特征根就可以得到转子振动的自然频率ωn,即进动角速度;因动量矩H=Jωn,故ωn 随转动角速度Ω改变;另一方面,临界角速度是与进动角速度相等的转动角速度;因此可以按照Ω=ωn的条件来计算转子的临界角速度;2由于陀螺力矩,转子有四个进动角速度;陀螺力矩对转子临界转速的影响是:正进动时,它提高了临界转速;反进动时,它降低了临界转速;13支撑刚度怎样影响转子的临界角速度答:减小支承刚度可以使转子的临界角速度显著降低,反而,增大支承刚度可以使转子的临界转速升高;14什么是收敛油楔、发散油楔答:顺着轴颈转向油膜厚度逐渐减小的油楔叫收敛油楔;厚度增加的叫做发散油楔;15利用轴承的平衡半圆说明轴承的工作原理,并说明转速和载荷对轴承稳定性的影响;答:平衡半圆:对于一个确定的轴承,当润滑油粘度及进油压已给定时,轴颈中心的静平衡位置e、ψ决定于轴颈转速Ω和静载荷ω ;当载荷ω的大小或者轴颈转速Ω变化时,位置也相应地变化,其轨迹近似地为一半圆弧,称为平衡半圆;当轴颈转速不变,承载ω=0时,轴颈中心与轴瓦轴心重合,即轴颈无偏心;随着载荷ω的增加,轴颈中心沿平衡半圆弧下降到轴瓦底部,旋转的轴颈把有粘度的润滑油仍发散区带入收敛区,沿轴颈旋转方向轴承间隙由大变小,形成一种油楔,使润滑油内产生压力;油膜内各点的压力沿轧制方向的合力就是油膜轴承的承载力;高速轻载轴承,其轴颈中心工作位置较高,而低速重载轴承,其工作位置较低,轴承较稳定;16什么是轴承的八个系数对轴承的性能有何影响答:轴承的八个系数:他们分别是刚度系数kxx、kxy、kyx、kyy;阻尼系数:cxx、cxy、cyx、cyy;系数kxx、kyy 相对应的弹性力是保守力,在轴心一周的涡动中做功为零,而cxx、cyy 对应的阻尼力恒做负功,亦即消耗能量;与kxy、kyx 对应的是非保守弹性力,它们与cxy、cyx 对应的阻尼力一样,在一周中作的功可为正即向转子系统输入能量,也可为负即消耗系统的能量,这取决于涡动轨迹形状、动力系数的大小和正负;如果一周涡动中,输入系统的能量小于各种阻尼所消耗的能量,那么涡动就越来越小趋于消失,这时系统是稳定的,反而,系统就是不稳定的;交叉动力系数的大小和正负对转子系统的稳定性起着重要作用;17什么是轴承的雷诺方程其基本假设是什么答:雷诺方程是进行轴承油膜分析的基本方程:R——轴颈半徂mp——油膜压力N/m2η——润滑油粘度N·s/ m2z——轴瓦的轴向坐标,原点取在中面上mt——时间s①油膜厚度较其长度来说是十分小的,故油膜压力沿油膜厚度方向可认为不变;②油的流动是层流;③润滑油是各向同性的,粘度在油膜厚度方向是常数;④润滑油与轴颈、轴瓦表面而间无滑动;⑤润滑油符合牛顿粘性定律,即剪应力与剪切率成正比;⑥油的惯性不计;18什么是紊流轴承理论答:当流体流动的Reynolds数足够高时,流动性质就仍层流转变为紊流;在大型高速机械及采用高密度低粘度润滑流体的某些特殊要求的机器中,就常遇到工作在紊流工况的轴承;紊流工况下的轴承功率消耗大,温升高,偏心率和油流量小,因而其动力特性包括稳定性也有很大不同;紊流润滑理论研究的中心问题是:1轴承在什么条件下工作,层流会不稳定而变为紊流,仍而它必须按紊流工况来设计;2在紊流工况下如何建立基本方程,计算紊流油膜中的速度及压力分布;19滚动轴承和滑动轴承的阻尼系数和刚度系数的取值范围是什么答:滚动轴承:滚珠轴承,一般可以认为:滚珠轴承的阻尼可以忽略,而刚度系数kxx=kyy,kxy=kyx=0;刚度系数的大小主要取决于滚珠和内外滚道接触区的预载荷,这取决于轴承安装方法、零件公差和轴承工作温度,实验测得的典型刚度系数为2×10的7次方至1×10的8次方N/m;滚柱轴承的刚度系数一般要10倍于上述数据;滑动轴承:刚度系数最大约为kxx=kyy=~20什么是长轴承理论和短轴承理论答:长轴承:这类轴承的长度比其直徂大得很多即L D,这样油膜压力沿周向的变化率比沿轴向的变化率大得多即p/θ>>p/z;短轴承:这种情况下认为轴承长度L较而其直徂D小得多,致使油膜压力沿周向的变化率 p/θ较而其沿轴向的变化率p/z可以忽略不计;21什么是浮环密封、静压轴承、阻尼轴承答:浮环密封:通常的密封环为一圆环,它籍高压油压紧在一个台阶上以防止液体或者气体的泄漏,环不转轴而间充满着压力油;一般环不轴是同心的,也即密封环是一个无徂向载荷、无偏心的全圆轴承;当转速Ω超过转子最低临界转速两倍以后,密封环就成为一个负阻尼器,趋于使转子失稳;静压轴承:滑动轴承的一种,是利用压力泵将压力润滑剂强行泵入轴承和轴而间的微小间隙的滑动轴承;静压轴承由外部的润滑油泵提供压力油来形成压力油膜,以承受载荷;在静压轴承中,高压油通过限流小孔进入几个油囊中,轴承的主要设计参数是限流小孔不轴承油膜对油的阻力比;当取比值为1时,油囊中的压力为供油压力Ps的一半,此时油膜刚度系数最大;阻尼轴承:阻尼轴承的内外环,可视作一个转速为零的无偏心全圆轴承,阻尼轴承是一个纯阻尼器;阻尼轴承的供油压力必须足够大,否则,油将仍油隙中挤出而阻尼轴承就失去作用;22什么是油膜力的分解及其对转子运动的影响答:油膜力的分解及其对转子运动的影响:将油膜对轴承的总压力F分解为轴颈中心O’点的徂向力Fe和周向力Fφ;分力Fe起支撑轴颈的作用,相当于转轴的弹性力;分力Fφ垂直于O’的向徂并顺着转动方向,使O’的速度增大,因而使向徂OO’增大;就是使轴颈失稳的力;23什么是油膜的半频涡动答:油膜引起涡动的准确频率稍小于转动角速度而半,这种涡动称为半频涡动;24什么是失稳角速度答:轴承油膜力引起转子运动失稳时的转子角速度称为失稳角速度;转子失稳的条件为σ=0,由这一条件可以求得失稳角速度;25什么是轴承的相似系数答:轴承相似性系数的表达式为为无量纲的常数,较大的K值用于大型转子及轴承,较小的K值用小型转子;26转速如何影响轴径中心、圆盘中心和涡动频率答:转速对涡动频率的影响:1对于较小的K载荷或质量较大、间隙较大、油的粘度较小、轴颈宽度较小,转子的涡动即自激振动的振幅在转动角速度Ω的较大范围内变化较小;这一范围大到实际上只有下限而没有上限;涡动频率在所考虑的转速范围内变化很小,可以认为一常数;2对于较大的K载荷或质量较小、间隙较小、油的粘度较大、轴颈宽度较大,涡动振幅随角速度Ω有明显的变化;当Ω稍大于2ωn 时,振幅最大值;不而前一种情形相反,当Ω继续增加时,振幅很快减小,直至涡动消失;涡动角速度ω随Ω的增加而增加;3当K非常大时,振幅岁角速度Ω改变的曲线,当Ω≈ 2ωn 时,发生油膜振荡;共振率为ωn≈ Ω/2;但这并与是非线性恢复力系统受激振力所引起的强迫振动,当Ω≈ 2ωn时,也会出现次谐振,如果转子同时出现自激振动和次谐振,则因两种振动频率很靠近,合成的振动有拍的现象;27油膜自激振动的特点是什么答:1自激振动即涡动只有当转动角速度Ω高于第一阶临界角速度时才有可能发生;2自激振动的频率大致等于转子的自然频率ωn;3自激振动不是共振现象;在大多数情况下,它的转速的大范围内随时可能出现,而且实际上往往不能确定这范围的上限;4自激振动能否出现的界限主要取决于轴承设计;在最不利的情况下,这一界限即失稳转速的下限约为临界转速的二倍;5自激振动是非常激烈的;如果轴承设计不好,则它的的振幅往往比不平衡质量引起的共振振幅还要大;6自激振动是正向涡动,不转动方向相同;7当转速逐渐升高时,自激振动往往要推迟发生升速越快,自激振动越要推迟8当自激振动已经发生后,如果降低转速,则它可以保持到低于升速时开始发生的转速;即使在升速缓慢而自激振动没有推迟的时候也是这样;28什么是静不平衡和动不平衡答:如果一个转子的离心惯性力系向质心C 简化成为一合力:则此转子具有静不平衡;一个转子的离心惯性力系向质心C 简化的一般结果是一个力和一个力偶,综合具有静不平衡和偶不平衡,这样的转子不平衡成为动不平衡;29什么是刚性转子和柔性转子答:如果转子的工作转速进低于其一阶临界转速,此时不平衡离心力较小而转子比较刚硬,因而不平衡力引起的转子挠曲变形很小不转子偏心量相比,可以加以忽略;这种转子称为刚性转子;反而,不平衡力引起的挠曲变形不能忽略的转子称为挠性转子或称柔性转子;30柔性转子的影响系数平衡方法是什么答:柔性转子平衡的影响系数法实质上是刚性转子平衡所用的两平面影响系数法的直接推广;对于刚性转子,校正平面取两个,平衡转速为一个;对挠性转子如果也这样做,就仅能保证在所选的那个平衡转速下的平衡,不能保证在一个转速范围内都达到平衡;如选临界转速为平衡转速,则工作转速下振动过大,相反如在工作转速下平衡,则转子往往不能通过临界转速;因此为平衡挠性转子,必须增加平衡转速的数目,相应的也许增加校正平面的数目,所以这是一种多平面多转速的影响系数法;设选取N 个平衡转速,校正平面有K 个,转子上选取M 个测振点;影响系数法的目标是保证在某一转速下,转轴上各点振动为零;为了使所构成的方程组有唯一解,也就是说要保证K=M×N,校正平面数目=测振点数目×平衡转速数目;31柔性转子的模态响应圆平衡方法是什么答:模态响应圆俗称振型圆,它是以转速为参变量在极坐标中绘制的某测振点振动响应的矢量端图;不同转速下的响应矢量连起来成为模态响应圆;在转子升速或降速时,连续测量可以得到模态响应圆;临界转速对应于响应圆的直徂;不平衡方向领先于临界转速时的响应90度;32.转子的临界转速当激振力的频率和转子系统的弯曲振动自振频率相接近的时候,转子发生共振;这时候转子的转速称为转子的临界转速;转子在该转速下运行时,转子会发生剧烈的振动,而偏离该转速值大于或小于一定范围后,旋转又趋于平稳;转子的临界转速实质上就是转子系统的偏心质量在转动过程中形成的激振力和系统发生共振时的转速;一个均布质量的转轴具有无穷多个自振频率,它在数值上和转子作横向振动的自振频率一样;按照频率数值的大小排列,称为转子的各阶自振频率 ;由于临界转速现象是激振力频率和转子自振频率相同时产生的共振现象;因此,转子的各阶自阶振频率就是转子的各阶临界转速,记作 ;转子具有无穷多阶临界转速;转子临界转速的大小,取决于转子的材料、几何形状和结构型式;因此,对一个具体的转子来说,临界转速的大小是一定的;转子系统的刚性愈大,转子的临界转速愈大;33.影响临界转速的因素一转子温度沿轴向变化对临界转速的影响在汽轮机中,尤其是高参数汽轮机中,沿转子轴向的温度变化是很大的;温度的变化引起转子材料弹性模量E沿转子轴向的变化;由式2-20可以看到,转子的临界转速与转子材料的弹性模量的平方根成正比;因此,弹性模量E的下降必然引起转子临界转速的下降;温度升高,E减小;二转子结构型式对临界转速的影响叶轮装在轴上使轴的刚度有一定程度的增加,因而提高了转子的临界转速;不同的转子结构型式影响是不一样的;叶轮回转力矩对临界转速的影响;对于直径比较大不是装在两个支承的正中间,甚至装在轴的悬臂端上的圆盘,在作弓形回旋时,将会产生回转力矩,使转子的临界转速发生变化可能提高,也可能降低;四轴系的临界转速和联轴器对临界转速的影响把一个单跨,二支点的转子连成了一个多支点的转子系统,称为轴系;在轴系中,由于相邻转子通过联轴器连接起来,轴的端部就不再是自由端;转子端部互相作用,就相当于在每个单跨转子的端部多了一个约束条件,使转子的刚性增加,从而引起该转子临界转速的加大;轴系的各阶临界转速总比单个转子的临界转速数值大;轴系是用联轴器连接;联轴器的刚性愈大,转子之间连接刚性愈大,因而相对于单个转子,轴系的临界转速升高亦愈多;五支承弹性对临界转速的影响实际上轴承座、轴瓦中起支承和润滑作用的油膜都不是绝对刚性的;33.转子临界转速的安全标准为了保证转子安全运行,就必须:•尽可能避开共振•对转子进行精确的平衡;如果透平的工作转速n小于转子的第一阶临界转速要求:nc1>1.2-1.25n;如果透平的工作转速n在转子的一阶和二阶临界转速之间要求:<n<;我国电力部门提出,对于固定式发电用汽轮发电机组,要求轴系的各阶临界转速一般应与工作转速避开;轴系各阶临界转速的分布应保证机组能够有安全的暖机转速,并进行超速试验;34.转子振动响应振动响应是旋转机械轴系重要的动态特性;它是指转子上存在质量不平衡造成的振动响应,包括响应的幅值和相位;这个特性用影响系数α来量度:α=振动响应/振动平衡不平衡响应特性决定了转子对已经存在的不平衡量或运转过程中突然出现的不平衡的响应程度;从轴系安全角度出发,希望这个响应越小越好;α小意味着同样的不平衡量所造成的转子的振动小,小的不平衡响应,可以减小动平衡的次数,减少运行中意外事故对设备带来的不良后果;35.轴系稳定性和动压滑动轴承汽轮发电机组功率的增加,导致转子轴颈的增大和轴系临界转速的下降,进而影响转子轴系工作的稳定性;(1)稳定性的基本概念高速旋转机器的转轴支承在径向滑动轴承上,转子轴颈为油膜所包阁,当外载荷W恒定并与油膜压力F1相平衡,转子轴颈中心将处于平衡位置O j c,0图2—15;实际上转轴在运转时不可能不受到扰动或冲击载荷此时轴颈中心将偏离平衡位置Oj如果转轴受扰动后,轴颈中心随时间的增加而逐渐趋向平衡位置,则认为是稳定的;如果随时间的增加,转子振动的振幅越来越大、或轴颈围绕平衡位置作“涡动”,则认为是不稳定的;轴颈受扰动其中心偏离平衡位置后,新位置的润滑油膜对轴颈产生一作用力,其方向与扰动方向有一偏位角;该作用力为扰动而引起的不平衡力,可分解为两个分力,即一个为沿扰动方向的分力,它是抗拒扰动的,还有一个垂直于扰动方涡动,其方向与轴颈的自转方向一致或相反; 向的分力,推动轴颈绕原平衡位置Ob。
旋转机械故障诊断旋转机械故障诊断旋转机械是指依靠转⼦旋转运动进⾏⼯作的机器,在结构上必须具备最基本的转⼦、轴承等零部件。
典型的旋转机械:各类离⼼泵、轴流泵、离⼼式和轴流式风机、汽轮机、涡轮发动机、电动机、离⼼机等。
⽤途:1、在⼤型化⼯、⽯化、压缩电⼒和钢铁等部门,某些⼤型旋转机械属于⽣产中的关键设备2、炼油⼚催化⼯段的三机组或四机组3、⼤化肥装置中的四⼤机组或五⼤机组4、⼄烯装置中的三⼤机组5、电⼒⾏业的汽轮发电机、泵和⽔轮机组6、钢铁部门的⾼炉风机和轧钢机组旋转机械可能出现的故障类型:1、转⼦不平衡故障2、转⼦不对中故障3、转轴弯曲故障4、转轴横向裂纹的故障5、连接松动故障6、碰摩故障7、喘振转⼦的不平衡振动机理及特性:旋转机械的转⼦由于受材料的质量分布、加⼯误差、装配因素以及运动中的冲蚀和沉积等因素的影响,致使其质量中⼼与旋转中⼼存在⼀定程度的偏⼼距。
偏⼼距较⼤时,静态下,所产⽣的偏⼼⼒矩⼤于摩擦阻⼒距,表现为某⼀点始终恢复到⽔平放置的转⼦下部,其偏⼼⼒矩⼩于摩擦阻⼒距的区域内,称之为静不平衡。
偏⼼距较⼩时,不能表现出静不平衡的特征,但是在转⼦旋转时,表现为⼀个与转动频率同步的离⼼⼒⽮量,离⼼⼒F=Mew2,从⽽激发转⼦的振动。
这种现象称之为动不平衡。
静不平衡的转⼦,由于偏⼼距e较⼤,表现出更为强烈的动不平衡振动。
虽然做不到质量中⼼与旋转中⼼绝对重合,但为了设备的安全运⾏,必须将偏⼼所激发的振动幅度控制在许可范围内。
1、不平衡故障的信号特征1)时域波形为近似的等福正弦波。
2)轴⼼轨迹为⽐较稳定的圆或椭圆,这是因为轴承座及基础的⽔平刚度与垂直刚度不同所造成。
3)频谱图上转⼦转动频率处的振幅。
4)在三维全息图中,转动频率的振幅椭圆较⼤,其他成分较⼩。
2、敏感参数特征1)振幅随转速变化明显,这是因为,激振⼒与⾓速度w是指数关系。
2)当转⼦上得部件破损时,振幅突然变⼤。
例如,某烧结⼚抽风机转⼦焊接的合⾦耐磨层突然脱落,造成振幅突然增⼤。
基于有限元法的转子轴承系统非线性特性研究摘要针对典型的转子轴承系统构造了一个复杂多因素并且能够比较真实地反映实际系统的非线性系统模型。
采用有限元方法将其离散化分为圆盘、 轴段和轴承座等单元,并对各单元 作了详细的动力分析, 当考虑油膜力耦合作用时, 广义力的求解引用了瑞利耗散函数, 推出 了油膜粘性阻尼力的非线性因素,再由拉格朗日方程得出系统的运动微分方程。
最后 关键词:陀螺力矩油膜力转子轴承系统有限元Finite element method based on nonlinear characteristics of rotor bearingAbstract A typical rotor-beari ng system for a complex multi-factor structure and the ability to truly reflect the actual system of nonlinear system model. Finite element method to the disc is divided into discrete, such as shafts and bearing units, each unit made a detailed and dynamic analysis, when considering the coupling of oil film force, the generalized Rayleigh power dissipation of the solution quoted function, introduced the film's nonlinear viscous damping factor,then the Lagra nge equati ons derived differe ntial equati ons of moti on. Fin ally, Key words : oil film force gyroscopic eleme nt rotor-beari ng system 等单元⑶。
A.1 传递距阵法分析程序 %main_critical.m %该程序使用Riccati传递距阵法计算转子系统的临界转速及振型 %本函数中均采用国际单位制 % 第一步:设置初始条件(调用函数shaft_parameters) %初始值设置包括:轴段数N,搜索次数M %输入轴段参数:内径d,外径D,轴段长度l,支撑刚度K,单元质量mm,极转动惯量Jpp[N,M,d,D,l,K,mm,Jpp]=shaft_parameters; % 第二步:计算单元的5个特征值(调用函数shaft_pra_cal) %单元的5个特征值: %m_k::质量 %Jp_k:极转动惯量 %Jd_k:直径转动惯量 %EI:弹性模量与截面对中性轴的惯性矩的乘积 %rr:剪切影响系数 [m_k,Jp_k,EI,rr]=shaft_pra_cal(N,D,d,l,Jpp,mm); % 第三步:计算剩余量(调用函数surplus_calculate),并绘制剩余量图 %剩余量:D1 for i=1:1:M ptx(i)=0; pty(i)=0; end for ii=1:1:M wi=ii/1*2+50; [D1,SS,Sn]=surplus_calculate(N,wi,K,m_k,Jp_k,JD_k,l,EI,rr); D1; pty(ii)=D1; ptx(ii)=w1 end ylabel(‘剩余量’); plot(ptx,pty) xlabel(‘角速度red/s’); grid on % 第四步:用二分法求固有频率及振型图 %固有频率:Critical_speed wi=50; for i=1:1:4 order=i [D1,SS,Sn]=surplus_calculate(N,wi,k,m_k,Jp_k,Jd_k,l,EI,rr); Step=1; D2=D1; kkk=1; while kkk<5000 if D2*D1>0 wi=wi+step; D2=D1; [D1,SS,Sn]=surplus_calculate(N,wi,K,m_k,Jp_k,Jd_k,l,EI,rr); end if D1*D2<0 wi=wi-step; step=step/2; wi=wi+step; [D1,SS,Sn] =surplus_calculate(N,wi,K,m_k,Jp_k,Jd_k,l,EI,rr); End D1; Wi; If atep<1/2000 Kkk=5000; end end Critical_speed=wi/2/pi*60 figure; plot_mode(N,l,SS,Sn) wi=wi+2; end %surplus_calculate,.m %计算剩余量 %(1)计算传递矩阵 %(2)计算剩余量 function [D1,SS,Sn]= surplus_calculate(N,wi,K,m_k,Jp_k,Jd_k,l,EI,rr); % (1)计算传递矩阵 %=============== %(a)初值设为0 %=============== for i=1:1:N+1 for j=1:1:2 for k=1:1:2 ud11(j,k.i)=0; ud12(j,k.i)=0; ud21(j,k.i)=0; ud22(j,k.i)=0; end end end for i=1:1:N for j=1:1:2 for k=1:1:2 us11(j,k.i)=0; us12(j,k.i)=0; us21(j,k.i)=0; us22(j,k.i)=0; end end end for i=1:1:N for j=1:1:2 for k=1:1:2 u11(j,k.i)=0; u12(j,k.i)=0; u21(j,k.i)=0; u22(j,k.i)=0; end end end %============ %(b)计算质点上传递矩阵―――点矩阵的一部分! %============ for i=1:1:N+1 ud11(1,1,i)=1; ud11(1,2,i)=0; ud11 (2,1,i)=0; ud11(2,2,i)=1; ud21(1,1,i)=0; ud21(1,2,i)=0; ud21 (2,1,i)=0; ud21(2,2,i)=0; ud22(1,1,i)=1; ud22(1,2,i)=0; ud22 (2,1,i)=0; ud22(2,2,i)=1; end %============ %(c)计算质点上传递矩阵―――点矩阵的一部分! %============ for i=1:1:N+1 ud12(1,1,i)=0; ud12(1,2,i)=(Jp_k(i)-Jd_k(i))*wi^2; %%%考虑陀螺力矩 ud12(2,1,i)=m_k(i)*wi^2-k(i); ud12(2,2,i)=0; end %============ %(d)以下计算的是无质量梁上的传递矩阵―――场矩阵 %计算的锥轴的us是不对的,是随便令的,在后面计算剩余量时,zhui中会把错误的覆盖掉 %============ for i=1:1:N us11(1,1,i)=1; us11(1,2,i)=1(i); us11 (2,1,i)=0; us11(2,2,i)=1; us12(1,1,i)=0; us12(1,2,i)=0; us12 (2,1,i)=0; us12(2,2,i)=0; us21(1,1,i)=1(i)^2/(2*EI(i)); us21(1,2,i)=(1(i)^3*(1-rr(i))/(6*EI(i)); us21(2,1,i)=1(i)/EI(i); us21(2,2,i)=1(i)^2/(2*EI(I)); us22(1,1,i)=1; us22(1,2,i)=1(i); us22 (2,1,i)=0; us22(2,2,i)=1; end %============ %此处全为计算中间量 %============ for i=1:1:N+2 Su (1,1,i)=0; Su (1,2,i)=0; Su (2,1,i)=0; Su (2,2,i)=0; Sn(1,1,i)=0; Sn (1,2,i)=0; Sn (2,1,i)=0; Sn(2,2,i)=0; SS (1,1,i)=0; SS (1,2,i)=0; SS (2,1,i)=0; SS (2,2,i)=0; end for i=1:1:2 for j=1:1:2 SS1(i,j)=0; Ud11(i,j)=0; Ud12(i,j)=0; Ud21(i,j)=0; Ud22(i,j)=0; Us11(i,j)=0; Us12(i,j)=0; Us21(i,j)=0; Us22(i,j)=0; end end %============ %(e)调用函数cone_modify修改锥轴的传递矩阵 %============ cone_modify(4,wi); cone_modify(5,wi); cone_modify(6,wi); cone_modify(7,wi); cone_modify(8,wi); cone_modify(16,wi); cone_modify(17,wi); cone_modify(18,wi); cone_modify(19,wi); cone_modify(22,wi); cone_modify(24,wi); %============ %(f)形成最终传递矩阵 %============ %Ud11 Ud12 Ud21 Ud22 为最终参与计算的传递矩阵 for i=1:1:N u11(:,:,i)=us11(:,:,i)*ud11(:,:,i)+us12(:,:,i)*ud21(:,:,i); u12(:,:,i)=us11(:,:,i)*ud12(:,:,i)+us12(:,:,i)*ud22(:,:,i); u21(:,:,i)=us21(:,:,i)*ud11(:,:,i)+us22(:,:,i)*ud21(:,:,i); u22(:,:,i)=us21(:,:,i)*ud12(:,:,i)+us22(:,:,i)*ud22(:,:,i); end u11(:,:,N+1)=ud11(:,:,N+1); u12(:,:,N+1)=ud12(:,:,N+1); u21(:,:,N+1)=ud21(:,:,N+1); u22(:,:,N+1)=ud22(:,:,N+1); for i=1:1:2 for j=1:1:2 SS1(i,j)=0; end end for i=1:1:N+1 ud11= u11(:,:,i); ud12= u12(:,:,i); ud21= u21(:,:,i); ud22= u22(:,:,i); SS(:,:,:i+1)=( ud11* SS1+ ud12)*inv(ud21* SS1+ ud22); Su(:,:,i)= ud21* SS1+ ud22; Sn(:,:,i)= inv(ud21* SS1+ ud22); %计算振型时用到 SS1=SS(:,:,i+1); end %======(2)计算剩余量====== D1=det(SS(:,:,N+2); for i=1:1:N+1 D1=D1*sign(det(Su(:,:,i)); %消奇点 end %======(2)不平衡响应值EE====== EE(:,:,n+2)=-inv(SS(:,:,N+2)*PP(:,:,N+2); for i=N+1:-1:1 EE(:,:,I)=Sn(:,:,i)*EE(:,:,i+1)-Sn(:,:,i)*UF(:,:,i); end
A.2 碰摩转子系统计算仿真程序 %main.m %该程序主要完成完成jeffcott转子圆周碰摩故障仿真 %===========第一步:设置初始条件 %rub_sign:碰摩标志,若rub_sign=0,说明系统无碰摩故障;否则rub_sign=1 %loca: 不平衡质量的位置 %loc_rub: 碰摩位置 %Famp: 不平衡质量的大小单位为:[g] %wi: 转速 单位为:[rad] %r: 偏心半径 单位为:[mm] %Fampl: 离心力的大小 单位为:[kg,m] %fai: 不平衡量的初始相位 [rad] clc clear [rub_sign loca loc_rub Famp wi r Famp1 fai]=initial_conditions % 第二步:设置转子系统的参数值 %N: 划分的轴段数 %density: 轴的密度 单位为:[kg/m^3 %Ef: 轴的弹性模量 单位为:[Pa] %L: 每个轴段的长度 单位为:[m]