下载文档原格式
最优化问题的算法迭代格式最优化问题的算法迭代格式最优化问题是指在一定的条件下，寻找使某个目标函数取得极值（最大值或最小值）的变量取值。
解决最优化问题的方法有很多种，其中较为常见的是迭代法。
本文将介绍几种常用的最优化问题迭代算法及其格式。
一、梯度下降法梯度下降法是一种基于负梯度方向进行搜索的迭代算法，它通过不断地沿着目标函数的负梯度方向进行搜索，逐步接近极值点。
该方法具有收敛速度快、易于实现等优点，在许多应用领域中被广泛使用。
1. 算法描述对于目标函数 $f(x)$，初始点 $x_0$ 和学习率 $\alpha$，梯度下降算法可以描述为以下步骤：- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$；- 更新当前点 $x_k$ 为 $x_{k+1}=x_k-\alpha\nabla f(x_k)$；- 如果满足停止条件，则输出结果；否则返回第 1 步。
2. 算法特点- 沿着负梯度方向进行搜索，能够快速收敛；- 学习率的选择对算法效果有重要影响；- 可能会陷入局部极小值。
二、共轭梯度法共轭梯度法是一种基于线性方程组求解的迭代算法，它通过不断地搜索与当前搜索方向共轭的新搜索方向，并在该方向上进行一维搜索，逐步接近极值点。
该方法具有收敛速度快、内存占用少等优点，在大规模问题中被广泛使用。
1. 算法描述对于目标函数 $f(x)$，初始点 $x_0$ 和初始搜索方向 $d_0$，共轭梯度算法可以描述为以下步骤：- 计算当前点 $x_k$ 的梯度 $\nabla f(x_k)$；- 如果满足停止条件，则输出结果；否则进行下一步；- 计算当前搜索方向 $d_k$；- 在当前搜索方向上进行一维搜索，得到最优步长 $\alpha_k$；- 更新当前点为 $x_{k+1}=x_k+\alpha_k d_k$；- 计算新的搜索方向 $d_{k+1}$；- 返回第 2 步。
2. 算法特点- 搜索方向与前面所有搜索方向都正交，能够快速收敛；- 需要存储和计算大量中间变量，内存占用较大；- 可以用于非线性问题的求解。
最优化方法及其Matlab程序设计习题作业暨实验报告学院：数学与信息科学学院班级：12级信计一班姓名：李明学号：49第三章 最速下降法和牛顿法一、上机问题与求解过程1、用最速下降法求212221216423),(x x x x x x f --+=的极小值。
解：仿照书上编写最速下降法程序如下：function [x,val,k]=grad(fun,gfun,x0)%功能：用最速下降法求解无约束化问题：min f(x)%输入：x0是初始点，fun,gfun分别是目标函数和梯度%输出：x,val分别是近似嘴有点和最优值，k是迭代次数maxk=5000;rho=;sigma=;%一开始选择时选择的rho和sibma选择的数据不够合理，此处我参照书上的数据编写数据k=0;epsilon=1e-5;while(k<maxk)g=feval(gfun,x0);%计算梯度d=-g;%计算搜索方向if(norm(d)<epsilon),break;endm=0;mk=0;while(m<20)%Armijo搜索if(feval(fun,x0+rho^m*d)<feval(fun,x0)+sigma*rho^m*g'*d)mk=m;break;%直接利用Armijo搜索公式,一开始的时候没有记住公式编写出现错误endm=m+1;endx0=x0+rho^mk*d;k=k+1;endx=x0;val=feval(fun,x0)%求得每一个的函数值然后仿照书上建立两个目标函数和梯度的M文件：function f=fun(x)f=3*x(1)^2+2*x(2)^2-4*x(1)-6*x(2);function g=gfun(x)g=[6*x(1)-4,4*x(2)-6]';选取初始点为']0,0[，调用函数程序，得出最小极值点为']6667.0[，极小值为8333500.1,，在界面框中输入的程序如下：.5[x,val,k]=grad('fun','gfun',x0)val =x =k =10从结果可以看出迭代次数为10次，如果选取不同的初值点则迭代次数不一样，但是极小值相同。
步长自适应的测量矩阵迭代优化方法沈子钰;汪立新【摘要】在压缩感知中,降低传感矩阵的列相干性可以提高重构精度.因为稀疏字典一般是固定的,所以目前主要通过优化测量矩阵来间接降低传感矩阵列相干性.提出一种改进的测量矩阵优化算法,使用梯度下降法更新测量矩阵并结合Barzilai-Borwen方法以及Armijo准则,使步长能够在迭代中自适应调整并保证算法收敛性.仿真实验表明,所提出的方法具有更快的收敛速度并且能够得到更优的测量矩阵.【期刊名称】《计算机工程与应用》【年(卷),期】2019(055)001【总页数】5页(P266-270)【关键词】压缩感知;测量矩阵优化;梯度下降;自适应步长【作者】沈子钰;汪立新【作者单位】杭州电子科技大学通信工程学院,杭州 310018;杭州电子科技大学通信工程学院,杭州 310018【正文语种】中文【中图分类】TN9111 引言压缩感知（Compressive Sensing，CS）[1]是一种新的稀疏信号采样和重建理论。
该理论中信号采样和压缩同时完成，这使得系统能够低于奈奎斯特采样频率采样，降低了系统的数据采样和储存成本。
传感矩阵是测量矩阵与稀疏字典的乘积，文献[2]分析了传感矩阵列相干性与信号精确重构所需稀疏度之间的关系。
列相干性越高说明传感矩阵越逼近正交，从而越有利于信号重构。
由于稀疏字典一般是固定的，所以目前研究主要集中在测量矩阵的优化上。
文献[2]和文献[3]分别引出了相关系数和平均相关系数的概念，相关系数反映的是传感矩阵列向量之间的最大相干性，而平均相关系数反映传感矩阵列向量之间的平均相干性。
相比约束等距性质（Restricted Isometry Property，RIP）[4]、Spark判别理论[5]等评价方法，相关系数以及平均相关系数计算简单，具有可行性，所以目前测量矩阵的优化研究主要集中在如何降低传感矩阵列向量的相关系数以及平均相关系数上。
Elad[3]是研究测量矩阵优化算法最早的学者之一。
一维搜索:1精确一维搜索精确一维搜索可以分为三类：区间收缩法、函数逼近法（插值法）、以及求根法。
区间收缩法：用某种分割技术缩小最优解所在的区间(称为搜索区间)。
包括：黄金分割法、成功失败法、斐波那契法、对分搜索法以及三点等间隔搜索法等。
优化算法通常具有局部性质，通常的迭代需要在单峰区间进行操作以保证算法收敛。
确定初始区间的方法：进退法①已知搜索起点和初始步长；②然后从起点开始以初始步长向前试探，如果函数值变大，则改变步长方向；③如果函数值下降，则维持原来的试探方向，并将步长加倍。
1.1黄金分割法：黄金分割法是一种区间收缩方法(或分割方法)，其基本思想是通过取试探点和进行函数值比较，使包含极小点的搜索区间不断缩短以逼近极小值点。
具有对称性以及保持缩减比原则。
优点：不要求函数可微，除过第一次外，每次迭代只需计算一个函数值，计算量小，程序简单；缺点：收敛速度慢；函数逼近法（插值法）：用比较简单函数的极小值点近似代替原函数的极小值点。
从几何上看是用比较简单的曲线近似代替原的曲线，用简单曲线的极小值点代替原曲线的极小点。
1.2牛顿法：将目标函数二阶泰勒展开，略去高阶项后近似的替代目标函数，然后用二次函数的极小点作为目标函数的近似极小点。
牛顿法的优点是收敛速度快，缺点是需要计算二阶导数，要求初始点选的好，否则可能不收敛。
1.2抛物线法：抛物线法的基本思想就是用二次函数抛物线来近似的代替目标函数，并以它的极小点作为目标函数的近似极小点。
在一定条件下，抛物线法是超线性收敛的。
1.3三次插值法：三次插值法是用两点处的函数值和导数值来构造差值多项式，以该曲线的极小点来逼近目标函数的极小点。
一般来说，三次插值法比抛物线法的收敛速度要快。
精确一维搜索的方法选择：1如目标函数能求二阶导数：用Newton法，收敛快。
2如目标函数能求一阶导数：1如果导数容易求出，考虑用三次插值法，收敛较快；2对分法、收敛速度慢，但可靠；3只需计算函数值的方法：1二次插值法, 收敛快，但对函数单峰依赖较强；2黄金分割法收敛速度较慢，但实用性强，可靠；4减少总体计算时间：非精确一维搜索方法更加有效。
第四章 非线性规划教学重点：凸规划及其性质，无约束最优化问题的最优性条件及最速下降法，约束最优化问题的最优性条件及简约梯度法。
教学难点：约束最优化问题的最优性条件。
教学课时：24学时主要教学环节的组织：在详细讲解各种算法的基础上，结合例题，给学生以具体的认识，再通过大量习题加以巩固，也可以应用软件包解决一些问题。
第一节 基本概念教学重点：非线性规划问题的引入，非线性方法概述。
教学难点：无。
教学课时：2学时主要教学环节的组织：通过具体问题引入非线性规划模型，在具体讲述非线性规划方法的求解难题。
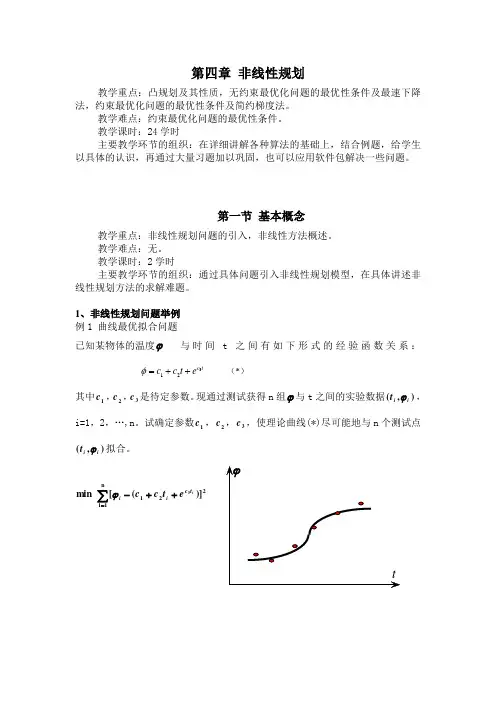
1、非线性规划问题举例例1 曲线最优拟合问题已知某物体的温度ϕ 与时间t 之间有如下形式的经验函数关系：312c t c c t e φ=++ （*）其中1c ，2c ，3c 是待定参数。
现通过测试获得n 组ϕ与t 之间的实验数据),(i i t ϕ，i=1，2，…,n 。
试确定参数1c ，2c ，3c ，使理论曲线(*)尽可能地与n 个测试点),(i i t ϕ拟合。
∑=++-n 1i 221)]([ min 3i t c i i e t c c ϕ例 2 构件容积问题通过分析我们可以得到如下的规划模型：⎪⎪⎩⎪⎪⎨⎧≥≥=++++=0,0 2 ..)3/1( max 212121222211221x x S x x x x a x x t s x x a V ππππ基本概念设n T n R x x x ∈=),...,(1，R R q j x h p i x g x f n j i :,...,1),(;,...,1),();(==,如下的数学模型称为数学规划(Mathematical Programming, MP)：⎪⎩⎪⎨⎧===≤q j x h p i x g t s x f j i ,...,1,0)( ,...,1,0)( ..)( min约束集或可行域X x ∈∀ MP 的可行解或可行点MP 中目标函数和约束函数中至少有一个不是x 的线性函数，称(MP)为非线性规划令 T p x g x g x g ))(),...,(()(1=T p x h x h x h ))(),...,(()(1=，其中，q n p n R R h R R g :,:，那么(MP )可简记为⎪⎩⎪⎨⎧≤≤ 0)( 0 ..)( min x h g(x)t s x f 或者 )(min x f X x ∈ 当p=0,q=0时，称为无约束非线性规划或者无约束最优化问题。
数学与计算科学学院 实 验 报 告
实验项目名称 使用非精确线搜索Armijo算法确定步长的 最速下降法 所属课程名称 最优化方法 实 验 类 型 算法编程 实 验 日 期
班 级 学 号 姓 名 成 绩 1
一、实验概述： 【实验目的】 1.通过实验掌握最速下降法的Matlab算法的基本步骤； 2.通过实验掌握Armijo算法确定步长； 3.掌握最速下降法的思想及迭代步骤。
【实验原理】 1.最速下降法： 最古老的优化方法，十九世纪中叶由Cauchy提出 思想 ：每次沿负梯度方向进行搜索
负梯度方向也称为最速下降方向： 举例：
算法步骤：
kx●
)(kxf
*x
● 等值线(面)
● 1kx
PxfxfxfpxfxfpxfPxfPxfpRpTkpkkkkkkTkn)(min||)(||)(- ||)(||)(-||)(||-||||||)(||-)(Schwarz-Cauchy,||||||||的解是下列问题时等号成立，即当取
不等式得由且事实上，对任意 2
.2,1:,4;33),(-.,||)(||2;0.0,1k1k0转步令步由线性搜索计算步长步；然后转步计算否则算法终止，则得解若步令精度给定初始点步kkdxxxfdxxfkRxkkkkkkkn
优点： .,最优解以较慢的速度无限接近但能优解代并没有求出其精确最最速下降法在有限次迭数极小化问题，对于简单的二元二次函
最速下降法的收敛性： 全局收敛性：
.,|||| ||)(|| ,0,降算法的全局收敛性我们很容易得到最速下所以且即方向与负梯度方向一致由于最速下降法的搜索kkkdxf
0||)(||lim }{Powell-WolfeArmijo ,kkkxfx满足代序列的迭搜索的最速下降法产生搜索或或采用精确搜索 ,,至多是线性的最速下降法的收敛速度由例子看到 收敛速度估计：
21
***1minmaxminmax||||,3.2 ||-||11-||-|| }{21)(min .,.,QxxxxxxxxxxqQxxxfQRqQT
Q
QkQkkTTn是问题的惟一解其中
）（
满足速下降法产生的点列则由采用精确搜索的最
问题：化考察如下二次函数极小的最大和最小特征值分别是和记对称正定设矩阵
3
)](-)([11-)(-)( )2.3(||-||21)-()-(21)(-)( 0)( )(,*2*12**T*****xfxfxfxfxxxxQxxxfxfqQxxfxqQxxfkkQ可以改写成所以则处且在由于对于二次函数.,( .,1 , ,1,,,)2.3(算法收敛很慢接近病态）较大时而当求出最优解算法只需一次迭代即可的所有特征值相等时即当特别最速下降收敛很快接近于当有关的条件数矩阵最速下降的收敛速度与看到由收敛速度估计式QQQ 结论：最速下降法的收敛速度比较慢，通常将其用在某些算法的初始阶段求较好的初始点或作为某些算法的间插步.
【实验环境】 Win 7； Matlab7.0
二、实验内容： 【实验方案】 1、求梯度； 2、向梯度相反的方向移动x，其中 为步长。如果步长足够小，则可以保证每一次迭代都在减小，但可能导致收敛太慢，如果步长太大，则不能保证每一次迭代都减少，也不能保证收敛。
3、循环迭代步骤2，直到x的值变化到使得在两次迭代之间的差值足够小，比如
0.00000001，也就是说，直到两次迭代计算出来的基本没有变化，则说明此时已经达到局部最小值了。 4、此时，输出x，这个x就是使得函数最小时的x的取值 。 【实验过程】 梯度下降法的计算过程就是沿梯度下降的方向求解极小值（也可以沿梯度上升方向求解极大值）。
其迭代公式为 ,其中 代表梯度负方向， 表示梯度方向上的搜索步长。梯度方向我们可以通过对函数求导得到，步长的确定比较麻烦，太大了的话可能会发散，太小收敛速度又太慢。一般确定步长的方法是由线性搜索算法来确定，即把下一个点的坐标ak+1看做是的函数，然后求满足f(ak+1)的最小值的 即可。 4
因为一般情况下，梯度向量为0的话说明是到了一个极值点，此时梯度的幅值也为0.而采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0即可，可以设置个非常小的常数阈值。
【实验结论】（结果） 梯度下降法处理一些复杂的非线性函数会出现问题，例如Rosenbrock函数：
其最小值在 处，函数值为 。但是此函数具有狭窄弯曲的山谷，最小点 就在这些山谷之中，并且谷底很平。优化过程是之字形的向极小值点靠近，速度非常缓慢。靠近极小值时收敛速度减慢。直线搜索时可能会产生一些问题。可能会“之字形”地下降。 【实验小结】（收获体会）
这次的实验报告，使得我们对这些算法的思想更加了解，在选择线性搜索的方法时，我们
深刻体会到各类参数设置对程序效率的重要性，不同的问题要选用合适的参数来求解，这样使得问题求解及程序运行的效率最高。通过不断地翻阅课本，剖析程序，我们最后实现了对程序的修改和完善，对提供的问题作出了较好的解答。总的来说，对无约束最优化的求解，每种方法在解决不同的问题中效果不能都达到最优，所以我们在实际应用中，要根据实际情况选择合适的方法，争取最大可能的尽快的接近最优。 本次实验不仅使我们基本了解了最优化的实用算法的结构及性能，而且也使得我们对matlab的一些编程技巧更加熟悉，收获很大。
三、指导教师评语及成绩： 评 语 评语等级
优 良 中 及格 不及格 1.实验报告按时完成,字迹清楚,文字叙述流畅,逻辑性强 2.实验方案设计合理 5
3.实验过程（实验步骤详细,记录完整,数据合理,分析透彻） 4实验结论正确.
成 绩： 指导教师签名： 批阅日期：
附录1：源 程 序 Armijo算法实现：
[plain] view plaincopy function mk = armijo( fun, xk, rho, sigma, gk )
assert( rho > 0 && rho < 1 ); assert( sigma > 0 && sigma < 0.5 );
mk = 0; max_mk = 100; while mk <= max_mk x = xk - rho^mk * gk; if feval( fun, x ) <= feval( fun, xk ) - sigma * rho^mk * norm( gk )^2 break; end mk = mk + 1; end
return; 最速下降法实现： [plain] view plaincopy function [opt_x, opt_f, k] = grad_descent( fun_obj, fun_grad, x0 )
max_iter = 5000; % max number of iterations EPS = 1e-5; % threshold of gradient norm
% Armijo parameters rho = 0.5; sigma = 0.2;
% initialization k = 0; xk = x0;
while k < max_iter k = k + 1; 6
gk = feval( fun_grad, xk ); % gradient vector dk = -1 * gk; % search direction
if norm( dk ) < EPS break; end
yk = feval( fun_obj, xk ); fprintf( '#iter = %5d, xk = %.5f, F = %.5f\n', k, xk, yk );
mk = armijo( fun_obj, xk, rho, sigma, gk ); xk = xk + rho^mk * dk; end
fprintf( '----------------------\n' ); if k == max_iter fprintf( 'Problem Not solved!\n' ); else fprintf( 'Problem solved!\n' ); end
% record results opt_x = xk; opt_f = feval( fun_obj, xk );
return;
附录2：实验报告填写说明 1．实验项目名称：要求与实验教学大纲一致。 2．实验目的：目的要明确，要抓住重点，符合实验教学大纲要求。 3．实验原理：简要说明本实验项目所涉及的理论知识。 4．实验环境：实验用的软、硬件环境。 5．实验方案（思路、步骤和方法等）：这是实验报告极其重要的内容。概括整个实验过程。 对于验证性实验，要写明依据何种原理、操作方法进行实验，要写明需要经过哪几个步骤来实现其操作。对于设计性和综合性实验，在上述内容基础上还应该画出流程图、设
