刘瑞梅初中数学中考计算题复习最全含答案
- 格式:docx
- 大小:382.02 KB
- 文档页数:13


WORD格式.初中数学计算题大全(一)8.( 1) (1) 233201102计算下列各题1 .(2) 0 1 tan60 0( 1) 162. 4 2( 9 3)7 1 1 32355449、( 1 ) -23+ ( -37)-(-12)+45;3. 1 4(1 0.5)1(4) 4 .(3) 027 121332375110.412 6604+ 3 2 + 386.0.64 3125225.811.( 1 )( 241)(16)287. 12- 1 - 2 123专业资料整理WORD格式.专业资料整理112. 4 3121813. 212 36314..(6x2x1 ) 3 x15.( 3) 2( 11) 1 ;4x32616. 18369 ( 52) 0(1 2)2321) ( 2) 33217.( 1 ) 12 ( 2718663WORD格式218.0.8 5 14.12 (1 )13194321.23. ( 32) 2(57 2 3 354|32|. 22 . 2 83)( 53)专业资料整理WORD格式参考答案1.解 =1 - |1-3 |-2+23=1+1- 3 - 2+2 3=3【解析】略2. 5【解析】原式=14-9=53.7 【解析】解:14(1 0.5)1 ( 4)83311123411878-1 4先算乘方,再算乘除,最后算加减,有括号的先算括号里面的。
注底数是意:4,有小数又有分数时,一般都化成分数再进行计算。
4.( 3)027 121=13321 32=.2332【解析】略5. 36. 4【解析】主要考查实数的运算,考查基本知识和基本的计算能力,题目简单,但易出错,计算需细心。
21、 4+3+38=2 3 2=33 125252、 0.64( -2) =0.82=48237.4 3 -232【解析】试题分析 :先化简,再合并同类二次根式即试题解析:12 -1 - 21=2 3-23考点 : 二次根式的运算.8.( 1 ) 32( 2 ) 9200【解析】( 1 )原式 =4+27+1=32(2 )原式 =23 ( 101 2 -99 2) (1分)=23( 101+99 ) (101-99)(分=23200 2 =9200(利用幂的性质求值。
1 .23621601214314175395243 40431511454233862328125647--8123220113212399101232210601651274311121241318123214 1531246612131321620212529363181712312712661833218243352741581920112|4120131124212223231|1|3333325=14-9=5387431511441312318118741-44011536414233832527------813229200121012-992(101-99)21220091-3;210121-23+-37--12+45410-30=-45-606512743606560127604335+50=-3011121212121312131431323157.21113262969276161212233633231212122312231712233411851451424334155275424335274155424335274158019-2.+2-=-2.1. 2.201212352122232------------------------------------------------------------------63253--------71 220130 3|1|012013567 8 10 111213+|3|+1 151612120130+||222+412 17112013|7|+0121819122012302452211|3|+162320130222122312+124122512+12612272829201322012420113011一.解答题(共3011211+12121211101220130+1+13|1|01201312+1111212451141144362744421811139210+31111111212原式第一项利用立方根的定义化简,第二项利用负数的绝对值等于它的相反数计算法则计算,第四项利用负指数幂法则计算,第五项利用1181311321132132214 3.140+|3|+120131415221612120130+||222+412121122424242+4 17112013|7|+01211211115218原式第一项利用立方根的定义化简,第二项利用二次根式的化简公式化简,第三项利用零指数幂法则计算,1451912121114+1+|12|142121112012302452121222311416314211|3|+16232013021)原式第一项利用负数的绝对值等于它的相反数计算,第二项先计算乘方运算,再计算除法运算,第2131234622212121121313122312+11)原式第一项利用负数的绝对值等于它的相反数计算,第二项利用特殊角的三212172+1+324121)原式第一项利用绝对值的代数意义化简,第二项利用零指数幂法则计算,第三项利用负指数幂法则21+13+3213212512+112112+126121)原式第一项利用特殊角的三角函数值化简,第二项利用零指数幂法则计算,212211118272282129201322012420112011201122420112242011+522420110301819126-6 3020151351251513 223113415322 2215113656 709422023432852213222330 920121451012456011 ---3622337956347181213343144201232221113.解方程(本小题共61 2532436431.60.20.5140||6015 233218342101216241940 17582818 192221121276521223201120+|4|×0.5+21 21 49322922121212423424 25 0116033230148 31|4|201634232212117538131383171. 2. 3. 4. 5.62-36:-363-17.=-1+1-9-8=-174172312x-2=3x+5 2x-3x=2+5x=-7262(2x+1)-(5x-1)=6x=-354113【解析】先把第二个方程去分母得3x-4y=-2,4113622114211222212221117363236322182323931410123211212111-192-111=-9÷9-18=-1-18=-192753796418=-28+30-27+14=-111221311326313 1532436112171217129128122121543326452431.60.20.529362762732661361263616220561235414试题分析:原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用特殊角的三角函数值计算,最后一项利用立方根定义化简计算即可得到2. 3.153222123x-3+6≥2x332181-3x+3-8+x 0-23223421012122221161747 189190 2021-40--19-24=-40+19-24=-45 2-5-8--28 3-1256712=6+10-74-22--22-23-12011=-4-4+85-32+|-4|×0.52+2-12942912=-4+1+521 312124234 712166 102244124322421 1212423412166224001160341313200116034131322425 =2-1+230-76=-48+8-36=-76316412 95。

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°•tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010•红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006•巴中)化简求值:,其中a=.12.(2010•临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010•綦江县)先化简,再求值,,其中x=+1.16.(2009•随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002•曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x—.25.(2011•新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011•南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011•武汉)先化简,再求值:÷(x ﹣),其中x=3. 30.化简并求值:•,其中x=21.. 2。

一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(2)解方程:=﹣.(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°(2)解方程:.25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.(2)化简,其中m=5.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006巴中)化简求值:,其中a=.12.(2010临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010綦江县)先化简,再求值,,其中x=+1.16.(2009随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x.24.先化简代数式再求值,其中a=﹣2.25.(2011新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011武汉)先化简,再求值:÷(x ﹣),其中x=3.30.化简并求值:,其中x=21.aa 2﹣a 2﹣1a +a ÷aa﹣a . 2。

初中数学中考计算题复习含答案集团标准化工作小组 [Q8QX9QT-X8QQB8Q8-NQ8QJ8-M8QMN]一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(2)解方程:=﹣.(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°(2)解方程:.25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.(2)化简,其中m=5.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006巴中)化简求值:,其中a=.12.(2010临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010綦江县)先化简,再求值,,其中x=+1.16.(2009随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x.24.先化简代数式再求值,其中a=﹣2.25.(2011新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011武汉)先化简,再求值:÷(x ﹣),其中x=3.30.化简并求值:,其中x=21. aa 2﹣a 2﹣1a +a ÷aa﹣a . 2。
一.解答题(共30小题)1.计算题:①;②解方程:.2.计算:+(π﹣2013)0.3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.4.计算:﹣.5.计算:.6..7.计算:.8.计算:.9.计算:.10.计算:.11.计算:.12..13.计算:.14.计算:﹣(π﹣)0+|﹣3|+(﹣1)2013+tan45°.15.计算:.16.计算或化简:(1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)17.计算:(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;(2).18.计算:.(1)19.(2)解方程:.20.计算:(1)tan45°+sin230°﹣cos30°?tan60°+cos245°;(2).21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°(2)解方程:=﹣.(1)计算:.22.(2)求不等式组的整数解.(1)计算:23.(2)先化简,再求值:(﹣)÷,其中x=+1.24.(1)计算:tan30°(2)解方程:.25.计算:(1)(2)先化简,再求值:÷+,其中x=2+1.26.(1)计算:;(2)解方程:.27.计算:.28.计算:.29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011.30.计算:.1.化简求值:,选择一个你喜欢且有意义的数代入求值.2.先化简,再求值,然后选取一个使原式有意义的x值代入求值.3.先化简再求值:选一个使原代数式有意义的数代入中求值.4.先化简,再求值:,请选择一个你喜欢的数代入求值.5.(2010?红河州)先化简再求值:.选一个使原代数式有意义的数代入求值.6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值.7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值.8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值.9.化简求值(1)先化简,再求值,选择你喜欢的一个数代入求值.(2)化简,其中m=5.10.化简求值题:(1)先化简,再求值:,其中x=3.(2)先化简,再求值:,请选一个你喜欢且使式子有意义的数字代入求值.(3)先化简,再求值:,其中x=2.(4)先化简,再求值:,其中x=﹣1.11.(2006?巴中)化简求值:,其中a=.12.(2010?临沂)先化简,再求值:()÷,其中a=2.13.先化简:,再选一个恰当的x值代入求值.14.化简求值:(﹣1)÷,其中x=2.15.(2010?綦江县)先化简,再求值,,其中x=+1.16.(2009?随州)先化简,再求值:,其中x=+1.17.先化简,再求值:÷,其中x=tan45°.18.(2002?曲靖)化简,求值:(x+2)÷(x﹣),其中x=﹣1.19.先化简,再求值:(1+)÷,其中x=﹣3.20.先化简,再求值:,其中a=2.21.先化简,再求值÷(x﹣),其中x=2.22.先化简,再求值:,其中.23.先化简,再求值:(﹣1)÷,其中x?.24.先化简代数式再求值,其中a=﹣2.25.(2011?新疆)先化简,再求值:(+1)÷,其中x=2.26.先化简,再求值:,其中x=2.27.(2011?南充)先化简,再求值:(﹣2),其中x=2.28.先化简,再求值:,其中a=﹣2.29.(2011?武汉)先化简,再求值:÷(x ﹣),其中x=3.30.化简并求值:?,其中x=21.a a 2﹣b2﹣1a+b ÷bb ﹣a.2。
汇总)初中数学中考计算题(最全)-含答案.doc1.解答题(共30小题)1.1 计算题:① 2+3=5;②解方程:x+5=10,解得x=5.1.2 计算:π+(π﹣2013)=2π-2013.1.3 计算:|1﹣|﹣2cos30°+(﹣)×(﹣1)2013|=|1-|-2cos30°+(-1)×(-1)2013||=|1-|-2×√3/2+1||=|1-√3+1|=|2-√3|。
1.4 计算:﹣(-2)+(-3)=1.1.5 计算:√(5+2√6)+√(5-2√6)=√2+√3.1.6 计算:(2+√3)(2-√3)=1.1.7 计算:(1+√2)²=3+2√2.1.8 计算:(1-√3)²=4-2√3.1.9 计算:(√2+1)²=3+2√2.1.10 计算:(√2-1)²=3-2√2.1.11 计算:(3+√5)(3-√5)=4.1.12 计算:(√3+1)(√3-1)=2.1.13 计算:(√2+√3)²=5+2√6.1.14 计算:﹣(π﹣3.14)+|﹣3|+(﹣1)2013+tan45°=0.1.15 计算:√3+√2-√6=√3-√2+√6.1.16 计算或化简:1)计算2﹣1﹣tan60°+(π﹣2013)+|﹣|=-tan60°-2011;2)(a﹣2)²+4(a﹣1)﹣(a+2)(a﹣2)=-3a²+10a-6.1.17 计算:1)(﹣1)2013﹣|﹣7|+(√2)﹣1=-√2-8;2)(2+√3)÷(√3-1)=1+√3.1.18 计算:(1+√2)(1-√2)=﹣1.1.19 解方程:x²+2x+1=0,解得x=-1.1.20 计算:1)tan45°+sin230°﹣cos30°•tan60°+cos245°=√2-1;2)(√2+1)²-(√2-1)²=4√2.1.211)|﹣3|+16÷(﹣2)³+(2013﹣)﹣tan60°=2010;2)解方程:(1-2x)²=3,解得x=√2﹣1.1.222)求不等式组:{x²-2x0},解得0<x<1.1.232)先化简,再求值:(√3+1)÷(√3-1)=2.1.241)计算:tan30°=√3/3;2)解方程:x²-2x+1=0,解得x=1.1.25 计算:1)√2-√3+√6=(√2-1)(√3-1);2)先化简,再求值:(√2+1)²+(√2-1)²=8.1.261)计算:(1-√2)÷(1+√2)=-1+√2;2)解方程:x²-2x+2=0,解得x=1-√3.1.27 计算:1)(√2+√3)²-(√2-√3)²=4√6;2)先化简,再求值:(x²+2x+1)÷(x²-1)=1+x。
一.解答题(共30小题) 1.计算题: ①;
②解方程:. 2.计算:+(π﹣2013)0. 3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013. 4.计算:﹣. 5.计算:. 6.. 7.计算:. 8.计算:. 9.计算:. 10.计算:. 11.计算:. 12.. 13.计算:. 14.计算:﹣(π﹣)0+|﹣3|+(﹣1)2013+tan45°.
15.计算:. 16.计算或化简: (1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|.
(2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2)
17.计算:
(1)(﹣1)2013﹣|﹣7|+×0+()﹣1;
(2). 18.计算:. 19.(1) (2)解方程:.
20.计算: (1)tan45°+sin230°﹣cos30°?tan60°+cos245°;
(2).
21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60°
(2)解方程:=﹣.
22.(1)计算:. (2)求不等式组的整数解.
23.(1)计算: (2)先化简,再求值:(﹣)÷,其中x=+1. 24.(1)计算:tan30° (2)解方程:. 25.计算: (1)
(2)先化简,再求值:÷+,其中x=2+1. 26.(1)计算:; (2)解方程:. 27.计算:. 28.计算:. 29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011. 30.计算:. 1.化简求值:,选择一个你喜欢且有意义的数代入求值. 2.先化简,再求值,然后选取一个使原式有意义的x值代入求值. 3.先化简再求值:选一个使原代数式有意义的数代入中求值. 4.先化简,再求值:,请选择一个你喜欢的数代入求值. 5.(2010?红河州)先化简再求值:.选一个使原代数式有意义的数代入求值. 6.先化简,再求值:(1﹣)÷,选择一个你喜欢的数代入求值. 7.先化简,再求值:(﹣1)÷,选择自己喜欢的一个x求值. 8.先化简再求值:化简,然后在0,1,2,3中选一个你认为合适的值,代入求值. 9.化简求值
一.解答题(共30小题)1.计算题:①]「 ■ ■ ■■ ■2.计算:匚-v ; + (n — 2013)②解方程:-■■ ;3.计算: |1 -230。
+ (- J0X(- 1)20134.计算:-:.J • I : - | ■:匚■W V丄5 .计算:i Fl ii ■' | : .:「--:::•;"[—;6_i「| 一一…' -.7•计算:|| 二i ill 门二_ 1 -8•计算:一_ 1 I 'I ■'b9•计算:.一 . 丄__ •10 •计算:7— ! - 卜--' …:-11. 计算:1: : I —•12 .:匸——- - : - ■- ' - . '13 .计算:丨:「―| 丿 - ■; : 3 -「了 - [ _ :14 .计算:1—(n—3.14 ) 0- 3 (- 1) 20134515•计算:. 1-乙U丄J16 •计算或化简:(1) 计算2 —1- "60° + (n- 2013) 0- | •217 .计算:(1) (- 1) 2013-| - 7「X「- ■ 0+ (')5(2)| 「:I .-:18 •计算: _「二•「川-•(1) -19.(2)解方程:,-丄20.计算:(1) 45° 230°—30° ?60°245°;(2) “ 一丨■. .. " :: - :' ■:-:-21 . (1) | - 316 一( —2) 3+ (2013—二0- 760(2)解方程:-.2it- 4 3i-62(2)求不等式组;.的整数解.23(1)计算:1 • 丁 I + , - -1』二"22 .("计算:...- .二''2013 ) °+|(2013 - K ) 02(2)先化简,再求值:(二-厶)一,,其中"1 .X _124. (1)计算:卜- . -:;--* 7*330 (2)解方程:厂J ;.25.计算:(1) 1. ■■■■ - -- ■ ■■ - : ■■2(2)先化简,再求值:' —「+ ,其中2 =+1.X2-1 x2+2x+l 玄726. (1)计算:—:■」•-;「+ ;(2)解方程:27. 计算:I .「- 「一.-.-I ■ :. . _28. 计算:辽D :' I 1. .1 ::29.计算:2011(1+ ")2013- 2 (1+ 匸)2012- 4 (1+匸)30.计算:I :'1. 化简求值:I,—; 二. —:,选择一个你喜欢且有意义的数代入求值.时1 X2- 12. 先化简,再求值,然后选取一个使原式有意义的x值代入X 1 X = 1求值.3.先化简再求值:选一个使原代数式有意义的数代入诗爲中求值4. 先化简,再求值:- :—,请选择一个你喜欢的数代入求值.可-1 a2 - a25. (2010?红河州)先化简再求值:'「’.选一个使原代数式有意义a+3 2a+o a+2的数代入求值.6.先化简,再求值:2(1—「)「「,选择一个你喜欢的数代入求值.■-J7 .先化简,再求值:(--1)一一,选择自己喜欢的一个x求值.x+3 『+6計98. 先化简再求值:化简——-「- ——.,然后在0, 1, 2, 3中选一个你认为a a合适的值,代入求值.9. 化简求值2(1)先化简,再求值,选择你喜欢的一个数代入求值.X2 -1 X2(2)化简1 1.-:,其中5.D+112 / 52(1)先化简,再求值:」:—’,其中3./ 一16 x _4 x+4(2)先化简,再求值:,请选一个你喜欢且使式子有意义的4y- 3 y- 2数字代入求值.2(3)先化简,再求值:•「:厂J其中2.K+2 X+2(4)先化简,再求值:厶,其中-1.J-9 垃 711. (2006?巴中)化简求值:. ,其中】a2 - 1 a+112. (2010?临沂)先化简,再求值:(—「)一 / J其中2.a+2 a+213. 先化简:,再选一个恰当的x值代入求值.时1 x2-114. 化简求值:(「- 1)-,其中2.x+1 X- 12 _15. (2010?綦江县)先化简,再求值,一——,其中「1.x+1 x+116. (2009?随州)先化简,再求值:「: :. 「' ,其中=1.X X17. 先化简,再求值:・+ :':,其中45°.x+1 計118. (2002?曲靖)化简,求值:(2)-(x-—),其中-1.1 _ S19. 先化简,再求值:(1+丄)一 ' ,其中-3.S_1x2- 120. 先化简,再求值:「- 一,其中2.a2 - 4 a_ 2?21. 先化简,再求值x -)其中2.22. 先化简,再求值:,:1 :」,其中工.23. 先化简,再求值:(:’-1)^ ",其中x24. 先化简代数式--再求值,其中-2.a+l a2 -125. (2011?新疆)先化简,再求值:(-+1)一^—,其中2.—x2-126. 先化简,再求值:’:-川」| ,其中2.3 -1 K -127. (2011?南充)先化简,再求值:匚―(竺丄-2),其中2.X2-1 X28. 先化简,再求值: _ 「" 11,其中-2.a a29. (2011?武汉)先化简,再求值:仝空一(x -勻,其中3.K X30. 化简并求值:匸亠'?:',其中2x+2 x- 1a 1 ba2^ + b.a1.3. (af1 3.a a21.解方程x - 41=0. 2。
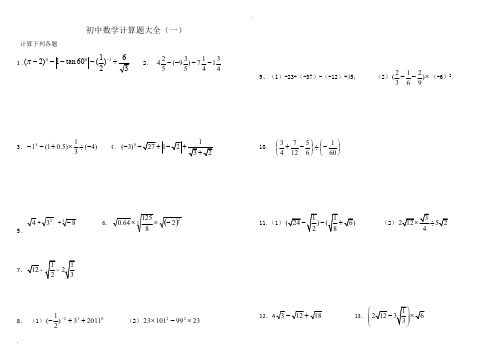
初中数学计算题大全(一) 计算下列各题 1 .36)21(60tan1)2(100
2. 431417)539(524 3.)4(31)5.01(14
4.01(3)271232
5.4+23 +3
8
6.2
32812564.0
7. (1)03220113)21( (2)23991012322 9、(1)-23+(-37)-(-12)+45; (2))926132((-6)2.
10. 6016512743
11.(1)11(24)(6)28 (2)3212524
12.418123 13.1212363
14..xxxx3)1246(
15.61)2131()3(2; 16.
20)21()25(2936318
17.(1))3127(12 (2)6618332
18.24335274158.0
19.11312()|32|43 20. 1020133112384。
21.. 22.112812623
23.2(32)(53)(53) 参考答案 1.解=1-|1-3|-2+23 =1+1-3-2+23
=3 【解析】略 2.5 【解析】原式=14-9=5
3.87【解析】解:)4(31)5.01(14 先算乘方,再算乘除,最后算加减,有括号的先算
括号里面的。注意:41-底数是4,有小数又有分数时,一般都化成分数再进行计算。
4.01(3)271232=1332132=23.
【解析】略 5.3 6.4 【解析】主要考查实数的运算,考查基本知识和基本的计算能力,题目简单,但易出错,计算需细心。 1、4+23 +38=232=3 2、2312550.64=0.82=482(-2) 7.43232- 【解析】 试题分析:先化简,再合并同类二次根式即可计算出结果. 试题解析:1122343212223232332--=--=- 考点: 二次根式的运算. 8.(1)32(2)9200 【解析】(1)原式=4+27+1 =32 (2)原式=23(1012-992) (1分) =23(101+99)(101-99)(2分) =232200=9200 (1分) 利用幂的性质求值。 利用乘法分配律求值。 9.(1)-3;(2)10 【解析】 试题分析:(1)把有理数正负数分开相加即可; (2)先算乘方,再运用乘法分配律,要注意不要漏乘即可. 试题解析: 解: (1)-23+(-37)-(-12)+45 = —23—37+12+45 = —23—37+12+45 =-3; (2))926132((-6)2 =)926132(36 =24—6—8 =10 考点:有理数的混合运算 10.-30 【解析】原式=
)60()6512743(=
)60(65)60(127)60(43=-45-35+50=
-30 11.(1)3264;(2)3210. 【解析】 试题分析:(1)先把二次根式化成最简二次根式之后,再合并同类二次根式即可求出答案; (2)先把二次根式化成最简二次根式之后,再进行二次根式的乘除法运算.
试题解析:(1)22=(26)(6)24原式 3264;
(2)31=43452原式 考点: 二次根式的化简与计算. 12. 13. 【解析】此题考查根式的计算
解:12.原式=4323322332.
13.原式=433633692. 答案:【小题1】 【小题2】 14.解:原式=313)23(xxx 【解析】略 15.7. 【解析】 试题分析:注意运算顺序. 试题解析:
2111(3)()326=2969276
考点:有理数的混合运算. 16.解:原式)12(1223)3633(23…………4分 12121223…………………………6分 1223………………………………………………8分 【解析】略 17.(1)334 (2)2 【解析】 试题分析:(1)11412(27)233333333 (2)233186633312 考点:实数运算 点评:本题难度较低,主要考查学生对平方根实数运算知识点的掌握。要求学生牢固掌握解题技巧。 18.514 【解析】 试题分析: 考点:有理数的运算 19.-2. 【解析】 试题分析:根据负整数指数幂的意义和绝对值的意义得到原式=23-4-3+2-3,然后合并即可. 试题解析:原式=23-4-3+2-3 =-2. 考点:1.二次根式的混合运算;2.负整数指数幂. 20.解:原式=12124=38=5。 【解析】针对有理数的乘方,绝对值,零指数幂,立方根化简,负整数指数幂5个考点分别进行计算,然后根据实数的运算法则求得计算结果。
21. 【解析】 试题分析:先进行二次根式化简,再进行计算即可. 试题解析:
考点: 二次根式的化简. 22.112812623 42323-------------------------------------------
--------------------------6分 423--------
23.2(32)(53)(53) 326253-----------------------------------------
-------------------------6分 726--------
【解析】略 初中数学计算题大全(二) 1.计算题: ①
; ②解方程:. 2.计算:+(π﹣2013)0. 3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013.
4.计算:﹣
. 5.计算:
. 6、
. 7.计算:. 8.计算:. 9.计算:. 10.计算:. 11.计算:. 12.. 13.计算:. 14.计算:﹣(π﹣3.14)0+|﹣3|+(﹣1)2013+tan45°. 15.计算:. 16.计算或化简: (1)计算2﹣1﹣tan60°+(π﹣2013)0+|﹣|. (2)(a﹣2)2+4(a﹣1)﹣(a+2)(a﹣2) 17.计算: (1)(﹣1)2013﹣|﹣7|+×0+()﹣1; (2). 18.计算:.
19.(1)
(2)解方程:. 20.计算: (1)tan45°+sin230°﹣cos30°?tan60°+cos245°;
(2). 21.(1)|﹣3|+16÷(﹣2)3+(2013﹣)0﹣tan60° (2)解方程:=﹣.
22.(1)计算:.
(2)求不等式组的整数解. 23.(1)计算: (2)先化简,再求值:(﹣)÷,其中x=+1. 24.(1)计算:tan30° (2)解方程:. 25.计算: (1) (2)先化简,再求值:÷+,其中x=2+1. 26.(1)计算:; (2)解方程:. 27.计算:. 28.计算:. 29.计算:(1+)2013﹣2(1+)2012﹣4(1+)2011. 30.计算:. 参考答案与试题解析 一.解答题(共30小题) 1.计算题: ①; ②解方程:. 考点: 解分式方程;实数的运算;零指数幂;特殊角的三角函专题: 计算题. 分析: ①根据零指数幂、特殊角的三角函数值、绝对值求出每②方程两边都乘以2x﹣1得出2﹣5=2x﹣1,求出方程的解答: ①解:原式=﹣1﹣+1﹣,
=﹣2; ②解:方程两边都乘以2x﹣1得: 2﹣5=2x﹣1, 解这个方程得:2x=﹣2, x=﹣1, 检验:把x=﹣1代入2x﹣1≠0, 即x=﹣1是原方程的解. 点评: 本题考查了解分式方程,零指数幂,绝对值,特殊角的易出错的题目,解②小题的关键是把分式方程转化成整
2.计算:+(π﹣2013)0. 考点: 实数的运算;零指数幂. 专题: 计算题. 分析: 根据零指数幂的意义得到原式=1﹣2+1﹣+1,然后合
解答: 解:原式=1﹣2+1﹣+1
=1﹣. 点评: 本题考查了实数的运算:先进行乘方或开方运算,再进幂.
3.计算:|1﹣|﹣2cos30°+(﹣)0×(﹣1)2013. 考点: 实数的运算;零指数幂;特殊角的三角函数值. 分析: 根据绝对值的概念、特殊三角函数值、零指数幂、乘方解答: 解:原式=﹣1﹣2×+1×(﹣1)
=﹣1﹣﹣1 =﹣2. 点评: 本题考查了实数运算,解题的关键是注意掌握有关运算4.计算:﹣
. 考点: 有理数的混合运算. 专题: 计算题. 分析: 先进行乘方运算和去绝对值得到原式=﹣8+3.14﹣1+9,解答: 解:原式=﹣8+3.14﹣1+9 =3.14. 点评: 本题考查了有理数的混合运算:先算乘方,再算乘除,