MATLAB的地震数据信号的分析

基于matlab的地震资料反演模拟作者：孙福玉来源：《中国科技纵横》2020年第06期摘要：本文对地球物理学反演的意义做了简要说明。

以地球物理反问题中的地震波褶积模型为例，通过理论分析和数学推导给出超定问题的最小二乘解法、先验信息的应用、线性反问题的广义反演法等多种常用方法，并通过matlab编程实现做最终成图对比分析。

关键词：超定问题;matlab编程;最小二乘法;先验信息;广义反演中图分类号：P631.4 文献标识码：A 文章编号：1671-2064（2020）06-0186-020 引言在自然界中，存在大量的客观事物，这些客观事物在传统物理学中，常常可以看成是一个系统。

这些事物包罗万象，小到原子大到宇宙。

一般来说，所有的客观事物都能用一定的物理量来描述，但不是所有的物理系统所包含的信息都能够被直接测量，有一部分物理系统的物理量只能通过间接测量。

在地球物理学领域的研究中，研究对象绝大多数都位于地表以下。

例如，研究地下地层的构造特征、寻找含油储集层、寻找矿产资源、寻找含水层。

将地下介质全部挖开去直接研究这些地质信息显然是不可能的。

为了全面的了解一个物理系统，往往希望获得尽可能多的描述系统的物理量，往往能够直接获取的物理量十分有限。

作为一种演绎性的研究手段，地球物理反演就是通过不断地推演系统中那些可以被直接观测的物理量与不可直接测量的物理量之间的联系。

达到通过已知信息去探索未知信息的一种方法。

反演问题一直以来都是地球物理学中的核心理论问题。

由于人类自身的局限性，获取深地信息的来源大都来源于地球表面，有极小一部分资料来自于对地球的直接探测，例如钻井信息。

所以人类对于地球的认识和研究终究还是要依靠有限的地球物理信息来实现，这些信息如何应用到实际研究中，就是反演问题的科研本质。

本文通过将理论方法用matlab编程实现，以反演地震子波为例，模拟地球物理反演过程。

1 超定问题的常规解法[1]通常，用物理模型去求解物理參数的过程叫做正演，而给定一系列物理模型的参数信息去求解物理模型的过程叫做反演。

MATLAB VMD程序1. 简介MATLAB VMD程序是一种用于信号处理和分析的工具，它基于VMD（Variational Mode Decomposition）方法，可以将复杂的信号分解为一系列振动模态。

VMD是一种自适应的信号分解方法，可以有效地从非线性和非平稳信号中提取出频率和幅度变化。

MATLAB VMD程序提供了一种简单而强大的方式来处理各种类型的信号，包括音频、图像、视频等。

它可以应用于多个领域，如通信、医学、地震学等，用于特征提取、噪声去除、模式识别等任务。

在本文中，我们将介绍MATLAB VMD程序的原理、使用方法以及一些实际应用案例。

2. 原理VMD方法是基于Hilbert-Huang变换（HHT）的一种信号分解方法。

它通过将信号分解为一系列振动模态函数（IMF），每个IMF代表一个特定频率范围内的振动成分，并且相邻IMF之间没有相位差异。

VMD方法的主要步骤如下：1.将原始信号进行预处理，包括去除趋势和高频噪声。

2.初始化参数，包括设置迭代次数和正则化参数。

3.使用VMD算法迭代地提取每个IMF，直到满足停止准则。

4.对于每个IMF，计算其局部频率和振幅。

VMD方法的优点在于它是一种自适应的方法，可以根据信号的特性来确定分解结果。

它对非线性和非平稳信号具有较好的适应性，并且能够提取出信号中的不同频率成分。

3. 使用方法MATLAB VMD程序提供了一种简单而灵活的方式来进行信号分解和分析。

以下是使用MATLAB VMD程序的基本步骤：1.导入信号数据：使用MATLAB的文件读取函数将原始信号导入到MATLAB环境中。

2.预处理信号：根据需要，可以对导入的信号进行预处理，如去除趋势、降噪等。

3.设置参数：根据实际情况，设置VMD方法所需的参数，如迭代次数、正则化参数等。

4.运行VMD程序：调用MATLAB VMD程序进行信号分解，并获取分解结果。

5.分析结果：对于每个IMF，可以计算其局部频率、振幅等特征，并进一步进行分析。

DDF模型是一种广泛应用于地震勘探和地球物理探测领域的数学模型，它可以帮助我们更好地理解地下构造和地震波传播规律。

在实际工程中，使用Matlab编程对DDF模型进行仿真和分析是非常常见的。

本文将介绍DDF模型的原理及其在Matlab程序中的实现。

一、DDF模型的原理1. 地震波传播原理在地球物理勘探中，地震波的传播是一项重要的研究内容。

地震波在地下介质中传播时会发生折射、反射和衍射等现象，这些现象受到介质物性的影响。

2. DDF模型概述DDF模型是一种基于弹性波动方程的数学模型，它可以描述地震波在介质中的传播过程。

DDF模型考虑了介质的弹性性质和几何形态，能够较准确地模拟地震波在复杂介质中的传播情况。

3. DDF模型的理论基础DDF模型基于弹性波动方程推导而来，其具体数学表达为一组偏微分方程。

通过对介质物性和边界条件的合理假设，可以得到DDF模型的数值解，从而实现对地震波传播的模拟和分析。

二、DDF模型的Matlab编程实现1. 编程环境准备在进行DDF模型的Matlab编程之前，首先需要准备好编程环境。

包括安装Matlab软件、了解Matlab的基本语法和数据处理方法等。

2. DDF模型的数值求解DDF模型的数值求解是整个Matlab编程过程的核心部分。

通过将DDF模型的偏微分方程离散化，可以得到一个关于介质物性和边界条件的代数方程组，利用Matlab的数值计算能力可以求解这组方程。

3. 结果可视化在得到DDF模型的数值解之后，还需要对模拟结果进行可视化处理。

可以利用Matlab的绘图功能，将地震波的传播情况以图像的形式清晰展现出来，便于工程人员进行分析和理解。

三、DDF模型在地震勘探中的应用实例1. 地震成像DDF模型在地震成像中有着广泛的应用。

通过对地震波在不同介质中的传播情况进行模拟，可以确定地下各层的构造和性质，为地球物理勘探提供重要的参考信息。

2. 地震波的反演地震波反演是地球物理勘探中的重要技术手段，可以通过对地震波在地下介质中的传播进行模拟，反推出地下介质的物性参数。

直达波抑制 Matlab1. 简介直达波是地震勘探中一种常见的干扰信号，它会对地震数据的处理和解释带来困难。

因此，直达波抑制是地震信号处理中的一个重要任务。

本文将介绍如何使用Matlab 来实现直达波抑制。

2. 直达波的特点直达波是地震信号中最早到达的一部分，它具有以下特点：•幅度较大：直达波的幅度通常比其他部分大几个数量级。

•频率较高：直达波的频率通常较高，一般在几十赫兹到几百赫兹之间。

•时间稳定：直达波的到达时间相对稳定，不随地震源位置的改变而改变。

3. 直达波抑制方法直达波抑制的目标是将直达波从地震数据中剔除或减弱，以便更好地分析和解释其他地震信号。

常用的直达波抑制方法包括：3.1. 时域方法时域方法是最常用的直达波抑制方法之一。

它通过对地震数据进行时域滤波或时域运算来实现直达波的抑制。

常见的时域方法包括：•均衡叠加法：将多道地震记录按照到达时间进行对齐和叠加，以增强直达波的幅度，从而更容易进行剔除。

•零相位滤波：通过设计合适的滤波器，将直达波的频率范围内的信号衰减，从而实现直达波的抑制。

3.2. 频域方法频域方法是另一种常用的直达波抑制方法。

它通过将地震数据转换到频域进行处理，然后再将处理后的数据转换回时域。

常见的频域方法包括：•傅里叶变换：将地震数据从时域转换到频域，然后通过对频域数据进行滤波或运算来实现直达波的抑制。

•小波变换：将地震数据分解为不同频率的小波系数，然后通过对小波系数进行阈值处理来实现直达波的抑制。

3.3. 自适应方法自适应方法是一种较为复杂但效果较好的直达波抑制方法。

它通过对地震数据进行自适应滤波或自适应运算来实现直达波的抑制。

常见的自适应方法包括：•自适应噪声抑制：通过对地震数据进行噪声估计和适应性滤波，将直达波的干扰信号减弱。

•自适应谱减法：通过对地震数据进行短时傅里叶变换和谱减法处理，将直达波的频率范围内的信号减弱。

4. 使用 Matlab 实现直达波抑制Matlab 是一个功能强大的科学计算软件，它提供了丰富的信号处理工具箱，可以方便地实现直达波抑制。

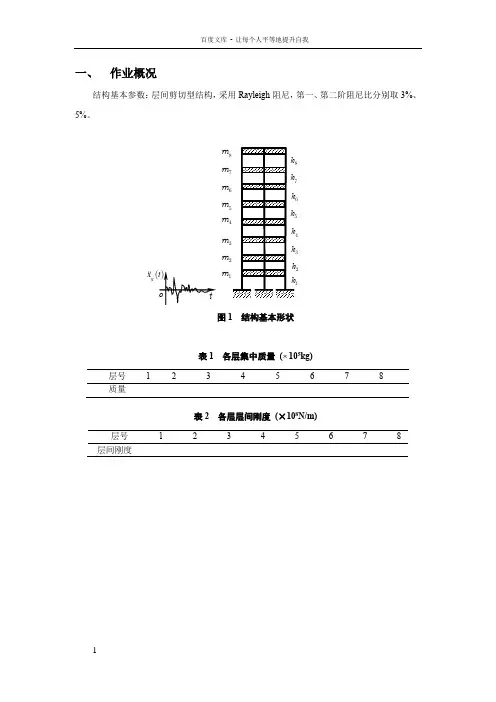
一、 作业概况结构基本参数：层间剪切型结构，采用Rayleigh 阻尼，第一、第二阶阻尼比分别取3%、5%。

图1 结构基本形状表1 各层集中质量 ( 105kg)层号 12345678质量表2 各层层间刚度 (×108N/m)层号 1 2 3 4 5 6 7 8 层间刚度m m m m m m m m ()g x t二、 频率及振型计算根据层间模型的假定，可以建立结构的质量矩阵以及刚度矩阵如下。

12345678000000000000000000000000000000000000000000000000000000003.400000000 3.400000000 3.200000000 3.20000 =0000 2.800000000 2.800000000 2.700000000 2.6m m m m m m m m ⎛⎫ ⎪ ⎪ ⎪ ⎪⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎛⎫ ⎝M 510kg ⎪⎪⎪⎪⎪⨯⎪⎪⎪⎪⎪⎪⎭ 11121314151617182122232425262728313233343536373841424344454647485152535455565758616263646566676871727374757677788182838485868788k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k ⎛ =⎝K 8420000002 3.8 1.8000000 1.8 3.6 1.8000000 1.8 3.6 1.8000 =10/000 1.8 3.6 1.8000000 1.8 3.4 1.6000000 1.6 3.2 1.6000000 1.6 1.6N m ⎫⎪⎪⎪⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎭-⎛⎫ ⎪-- ⎪ ⎪-- ⎪-- ⎪⨯ ⎪-- ⎪-- ⎪ ⎪-- ⎪ ⎪-⎝⎭根据上面求得的质量、刚度矩阵，即可求解特征方程：20K M（1）求解自振频率以及阵型向量已经演变成为典型的求解矩阵特征值以及特征向量的问题，特征值即为圆频率2，特征向量即为振型向量。

时频分析在地震数据处理中的应用摘要：经典的傅立叶分析只适用于分析平稳信号，而不适用于非平稳信号。

为了分析非平稳信号，我们采用时频分析方法。

时频分析能够清楚的揭示信号的时变频谱特征，是对时变、非平稳信号进行分析与处理的有力工具。

本文介绍了时频分析中常用的STFT和Wigner－Ville 分布和S变换的特点，并利用Matlab对一个地震信号进行时频分析的实现。

关键词：时频分析；短时傅立叶变换（STFT）；S变换；Wigner－Ville分布引言在传统的信号处理领域，基于Fourier 变换的信号频域表示及其能量的频域分布揭示了信号在频域的特征，它们在传统的信号分析与处理的发展史上发挥了极其重要的作用。

但是，Fourier 变换是一种整体变换，即对信号的表征要么完全在时域，要么完全在频域，作为频域表示的功率谱并不能告诉我们其中某种频率分量出现在什么时候及其变化情况。

然而，在许多实际应用场合，信号是非平稳的，其统计量（如相关函数、功率谱等）是时变函数。

这时，只了解信号在时域或频域的全局特性是远远不够的，最希望得到的乃是信号频谱随时间变化的情况。

为此，需要使用时间和频率的联合函数来表示信号，这种表示简称为信号的时频表示。

时频分析方法旨在通过构造一种时间和频率的密度函数，将一个一维的时间信号以二维的时间一频率函数形式表示出来，以揭示信号中所包含的频率分量及其随时间的变化特性。

这使我们不但能够同时掌握非平稳信号的时域及频域信息，而且可以清楚地了解非平稳信号的频率是如何随时间变化的。

通过时频分析方法技术对地震信号进行分析处理可在获得地震信号的瞬时频率、瞬时相位、瞬时振幅等瞬时参数的同时获得时频谱图等重要时频域信息，实现对地震信号的边缘检测、属性提取等。

时频分析是非平稳信号分析处理领域的重要方法，时频分布的基本任务是建立一个函数，要求这个函数能够同时用时间和频率来描述信号的能量密度。

如果有了这样的一个分布，就可以计算某一确定的频率和时间范围内能量的百分率、计算某一特定时刻的频率密度、计算该分布的整体和局部的各阶矩。

eemd的matlab代码EMD(Empirical Mode Decomposition)是一种基于自适应数据分解技术的信号处理方法，将数据分解成一系列本征模函数(EMD)，然后进行频率分析和时频分析。

EMD的最大好处是在信号分解过程中不需要做任何先验假设或者预处理，同时分解的本征模态函数（IMF)是时频局部化的，因而可以很好地处理非线性和非平稳信号。

EMD方法在地震学、金融和医学等领域得到了广泛应用。

EMD的matlab代码实现：1. 打开matlab2. 打开编辑器3. 新建一个文件，命名为emd.m4. 输入以下代码：function [imf,residual]=emd(x)% EMD% Given signal x (1,n), return IMFs in rows of matrix IMF (max num IMFs= n-1) and residual in vector res.n=length(x);if n<3error('Input signal length must be greater than 3.');endh=hilbert(x);x=h.*conj(h);x=x-mean(x);r=x;k=1;while k<=12 && ~issparse(r)d=r;for i=1:nminx=min([d(1:i-1) Inf d(i+1:n)]);max1=max(d(1:i-1));max2=max(d(i+1:n));if minx==Infcontinueendif x(i)>=max1 && x(i)>=max2 && x(i)>=minx d(i)=0;endendIMF(k,:)=r-d;r=d;if all(abs(IMF(k,:)))<.1*eps*max(abs(x))IMF(k,:)=[];breakendk=k+1;endresidual=x-sum(IMF);residual=real(h).*sign(residual);imf=real(h).*sign(IMF);%5. 保存文件6. 在matlab命令窗口中输入emd(数据)，即可进行EMD分解。

多点地震动合成matlab多点地震动合成是指将多个地震动记录合成为一个总体地震动记录的过程。

这种合成可以用于结构设计、地震工程和地震研究等领域。

在matlab中，可以使用不同的方法进行多点地震动合成，包括线性组合法、相对时程法和频率域法等。

一、线性组合法线性组合法是最常用的一种多点地震动合成方法。

其基本思想是通过将不同点的地震动记录按一定比例加权相加，得到总体地震动记录。

具体步骤如下：1. 导入地震动记录数据首先需要导入各个点的地震动记录数据。

假设有n个记录点，每个记录点的数据可以表示为一个长度为m的向量，其中m表示时间步数。

2. 设置权重系数根据实际情况设置各个点的权重系数。

权重系数反映了各个点对总体地震动影响的大小，可以根据距离、场址条件等因素进行确定。

3. 线性组合计算将各个点的地震动数据按照权重系数进行加权相加，得到总体地震动数据。

具体计算公式如下：```total_motion = w1 * motion1 + w2 * motion2 + ... + wn * motionn```其中，total_motion表示总体地震动数据，motion1、motion2、...、motionn表示各个点的地震动数据，w1、w2、...、wn表示相应的权重系数。

4. 结果输出将合成得到的总体地震动数据进行输出，可以保存为文件或进行后续分析。

二、相对时程法相对时程法是另一种常用的多点地震动合成方法。

其基本思想是通过比较不同点的地震动记录的时程特征，选取某个参考点作为基准，并将其他点的地震动记录与该参考点进行比较和调整，最终得到总体地震动记录。

具体步骤如下：1. 导入地震动记录数据同样需要导入各个点的地震动记录数据。

2. 选择参考点根据实际情况选择一个参考点作为基准。

通常选择具有较好场址条件或与其他点距离较近的点作为参考点。

3. 相对时程调整将其他点的地震动记录与参考点进行比较，并根据差异进行相对时程调整。

matlab地震勘探课程设计一、课程目标知识目标：1. 理解地震勘探的基本原理，掌握运用MATLAB进行地震数据处理和分析的相关知识。

2. 学习MATLAB的基本操作，包括数据导入、数据预处理、数据可视化等。

3. 掌握地震波传播、反射、折射等基本概念，并运用MATLAB进行简单地震模型的构建。

技能目标：1. 能够独立运用MATLAB进行地震数据读取、处理和展示，提高实际操作能力。

2. 培养运用MATLAB解决地震勘探领域实际问题的能力，包括地震波场模拟、地震资料解释等。

3. 培养团队协作能力，通过小组讨论、共同解决问题，提高沟通与协作技巧。

情感态度价值观目标：1. 激发学生对地球物理学和地震勘探领域的兴趣，培养探索自然、热爱科学的精神。

2. 培养学生面对复杂问题时的耐心、细心和毅力，提高克服困难的信心。

3. 强化学生的环保意识，认识到地震勘探在资源勘探、环境保护等方面的重要性。

课程性质：本课程为实践性较强的学科，要求学生结合地震勘探理论，运用MATLAB软件进行实际操作。

学生特点：学生具备一定的地震勘探理论基础，但对MATLAB软件操作相对陌生。

教学要求：注重理论与实践相结合，以实例为主线，引导学生通过实际操作掌握MATLAB在地震勘探中的应用。

将课程目标分解为具体的学习成果，便于教学设计和评估。

二、教学内容1. 地震勘探基本原理回顾：地震波传播、反射、折射等基本概念，波速、反射系数等关键参数。

2. MATLAB软件入门：软件安装、界面介绍、基本操作命令和数据类型。

3. 地震数据处理：数据导入与导出、数据清洗、数据插值、数据可视化等。

4. 地震波场模拟：利用MATLAB构建地震波场模型，模拟地震波的传播过程。

5. 地震资料解释：介绍地震资料解释的基本方法，运用MATLAB进行地震资料解释实践。

6. 实际案例分析：分析典型地震勘探案例，运用MATLAB解决实际问题。

教学大纲安排：第一周：地震勘探基本原理回顾，MATLAB软件入门。

matlab occam反演算法-回复什么是Matlab Occam反演算法？Matlab Occam反演算法是一种基于回归分析和最小二乘法的反演方法。

它主要用于实现地球物理勘探中的地下介质属性的定量分析。

Occam 反演算法通过将地震资料和已知的地震波速模型进行比较，从而推导出地下介质的物理特征。

虽然Occam反演算法在地球物理勘探领域广泛应用，但在Matlab中的实现还相对较新。

Matlab是一种专业的科学计算软件，提供了强大的数值计算和数据分析功能。

Matlab的优势在于其高度可扩展性和简单易用的编程语言。

通过Matlab，我们可以使用Occam反演算法来处理大量的地震数据，并可视化地下介质属性。

首先，为了使用Matlab Occam反演算法，我们需要了解一些基本原理。

Occam反演算法基于观测数据和地震模型之间的差异推导出地下介质的物理特性。

地震模型是由介质的地震波速度和密度等属性组成的。

通过在已知的地震模型上进行反演，我们可以得到未知介质的属性。

在开始Matlab Occam反演算法之前，我们需要准备地震数据和起始模型。

地震数据是通过地震勘探仪器获取的，记录了地震波传播过程中的信号变化。

起始模型是一个已知的地震波速度模型，用于与观测数据进行比较。

接下来，我们通过编写Matlab代码来实现Occam反演算法。

首先，我们需要导入地震数据和起始模型。

Matlab提供了读取和处理数据的函数，可以方便地将地震数据导入到Matlab中。

然后，我们需要根据地震数据和起始模型进行模拟。

在Matlab中，我们可以使用地震波传播的方程来模拟地震数据。

通过改变地下介质的参数，如波速度和密度，我们可以得到不同的模拟数据。

接下来，我们需要将观测数据和模拟数据进行比较。

通过计算观测数据和模拟数据之间的差异，我们可以得到反演误差。

为了最小化反演误差，我们可以使用最小二乘法。

最小二乘法是一种常见的数据拟合方法，它通过优化参数来最小化观测数据和模拟数据之间的差异。