401轴对称(作业)

用坐标表示轴对称练习题及答案 （时刻20分钟，满分50分） （一）基础测试： 分别写出下列各点关于x 轴和y 轴对称的点的坐标：（每小题2分，共20分） （1）（3，4）关于x 轴的对称点的坐标是（ ， ）（2）（1，－2）关于x 轴的对称点的坐标是（ ， ）（3）（－4，－2）关于x 轴的对称点的坐标是（ ， ）（4）（0，5）关于x 轴的对称点的坐标是（ ， ）（5）（a ，b ）关于x 轴的对称点的坐标是（ ， ）（6）（－7，21）关于y 轴的对称点的坐标是（ ， ） （7）（－2，－2）关于y 轴的对称点的坐标是（ ， ）（8）（2，0）关于y 轴的对称点的坐标是（ ， ）（9）（0，0）关于y 轴的对称点的坐标是（ ， ）（10）（a －b ，a －b ）关于y 轴的对称点的坐标是（ ， ）（二）能力测试：（第1－3题每题3分，第4题10分）1．点P 在第四象限内，P 点到x 轴的距离为2，到y 轴的距离为3，则P 点关于y 轴的对称点的坐标为 ．2．已知P （3，2a-5）与Q （3，a+2）关于x 轴对称，则a= ．3．如图，以矩形ABCD 的中心为原点建立坐标系．点A 的坐标是（3，2），则点B 的坐标是 ，点C 的坐标是 ，点D 的坐标是 ．4．如下图，在网格图中作出△ABC 关于x 轴和y 轴对称的图形．（三）拓展测试：如图，方格纸中每个小方格差不多上边长为1的正方形，我们把以格点连线为边的多边形称为“格点多边形”．如图（一）中四边形ABCD确实是一个“格点四边形”．（1）求图（一）中四边形ABCD的面积；（5分）（2）在图（二）方格纸中画一个格点三角形EFG，使△FEG的面积等于四边形ABCD 的面积且为轴对称图形．（6分）参考答案（一）（1）（3，－4）（2）（1，2）（3）（－4，2）（4）（0，－5）（5）（a，－b）（6）（7，21） （7）（2，－2）（8）（－2，0）（9）（0，0）（10）（b －a ，a －b ）(二)1．（－3，2）2．13．（3，－2） （－3，－2） （－3，2）4．（三）解：（1）方法一：1642S =⨯⨯ 12=方法二：11114621413423122222S =⨯-⨯⨯-⨯⨯-⨯⨯-⨯⨯= （2）（只要画出一种即可）。

轴对称作图及实际应用（作图）（北师版）一、单选题(共10道，每道10分)1.如图1，已知线段MN，在MN上求作一点O，使OM=ON．如图2用尺规作图作出了点O，下列作图语言叙述正确的是( )A.分别以点M，点N为圆心，任意长为半径作弧，两弧相交于点A和点B；作直线AB交MN于点O，点O即为所求．B.分别以点M，点N为圆心，以大于长为半径作弧，两弧相交于点A和点B；作直线AB交MN于点O，点O即为所求．C.以点M为圆心，任意长为半径作弧，再以点N为圆心，大于长为半径作弧，两弧相交于点A和点B；作直线AB交MN于点O，点O即为所求．D.分别以点M，点N为圆心，任意长为半径作弧，两弧相交于点A和点B；作直线AB，直线AB即为所求．答案：B解题思路：试题难度：三颗星知识点：尺规作图2.平面内，过直线外一点作已知直线的垂线最终都转化为下列哪一种基本作图( )A.作一个角等于已知角B.作一条线段等于已知线段C.作已知角的角平分线D.作已知线段的垂直平分线答案：D解题思路：试题难度：三颗星知识点：尺规作图3.如图1，已知A为直线MN外一点，求作直线AB，使AB⊥MN．如图2用尺规作图作出直线AB，下列叙述：①任取一点P；②以点A为圆心，AP长为半径作弧，交MN于C，D两点；③分别以点C、点D为圆心，以大于长为半径作弧，两弧交MN下方于一点B；④作直线AB．直线AB即为所求．其中错误的是( )A.①B.②C.③D.④答案：A解题思路：试题难度：三颗星知识点：尺规作图4.如图，A，B，C三个村庄联合打井，为使井到三个村庄的距离相等，下列确定水井的位置的说法中正确的是( )A.连接AB，AC，BC，作线段AB的垂直平分线MN，作∠ABC的角平分线BD交直线MN于点P，点P即为水井的位置B.连接AB，AC，作线段AB的垂直平分线MN，作线段AC的垂直平分线EF交直线MN于点P，点P即为水井的位置C.连接AB，AC，BC，作∠ABC的角平分线BD，作∠BAC的角平分线AE交BD于点P，点P 即为水井的位置D.作直线AB，BC，过点A作BC的垂线MN，过点C作AB的垂线EF交MN于点P，点P即为水井的位置答案：B解题思路：试题难度：三颗星知识点：尺规作图5.在高速公路的同侧有两个化工厂A，B，为了便于两厂的工人看病，市政府计划在公路边上修建一所医院，使得两个工厂的工人到医院的距离相等，关于医院位置，下列说法正确的是( )A.连接BA并延长交直线于点P，点P即为医院的位置B.连接AB，取AB的中点C，过点C作直线的垂线MN交直线于点P，点P即为医院的位置C.过点B作直线的垂线MN交直线于点P，点P即为医院的位置D.连接AB，作线段AB的垂直平分线交直线于点P，点P即为医院的位置答案：D解题思路：试题难度：三颗星知识点：尺规作图6.为打造“宜居城市”，某市拟在新竣工的矩形广场的内部修建一个音乐喷泉，要求音乐喷泉M到广场的两个入口A，B的距离相等，且到广场管理处C的距离等于A，B之间距离的一半，A，B，C的位置如图所示．用尺规作图作出音乐喷泉M的位置，下列作法正确的是( )A.分别作AB，BC的垂直平分线，两直线交于点MB.分别作AB，AC的垂直平分线，两直线交于点MC.作AB的垂直平分线，以点C为圆心，以长为半径作弧交AB的垂直平分线于点MD.作AB的垂直平分线，以点C为圆心，以长为半径作弧交AB的垂直平分线于点M答案：C解题思路：试题难度：三颗星知识点：尺规作图7.如图，已知∠AOB及其内部两点C，D，求一点P，使PC=PD，并且P点到∠AOB的两边的距离相等．用尺规作图作出点P的位置，下列作法正确的是( )A.连接CD，作CD的垂直平分线MN与∠AOB的角平分线OE，MN与OE的交点P即为所求B.作直线CD，作∠AOB的角平分线OE，OE与CD的交点P即为所求C.连接OC，OD，分别作OC，OD的垂直平分线MN，EF，MN与EF的交点P即为所求D.连接CD，作CD的垂直平分线MN，MN与OA的交点P即为所求答案：A解题思路：试题难度：三颗星知识点：尺规作图8.P是∠AOB内一点，分别作点P关于直线OA，OB的对称点，，连接，，则下列结论正确的是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：轴对称的性质9.如图，直线是一条河，P，Q两地位于的同侧，欲在上的某点M处修建一个水泵站，向P，Q两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则铺设的管道最短的是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：轴对称——最值问题10.如图所示，正方形ABCD，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC 上有一点P，使PD+PE最小，下列作图求出点P的位置，其中正确的是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：轴对称——最值问题。

轴对称中的作图题由于与轴对称有关的作图题，能有效的考查同学们的动手操作能力和空间想象能力，一直是考试的热点，下面就这方面的问题选取数例加以归析，供同学们参考。

一、画轴对称例1、如图，已知△ABC和直线MN，画出△EFG，使△EFG与△ABC关于直线MN对称。

分析：只需分别作△ABC的三个顶点A、B、C的对称点E、F、G，然后顺次连结E、F、G即可。

解：方法一：作AO⊥MN，垂足为O，在AO的延长线上截取OE=OA，点E就是点A关于直线MN的对称点，同法画点B、C的对称点F、G，然后顺次连结E、F、G得△EFG。

则△EFG就是所求。

方法二：也可以利用全等知识进行作图，即先出A、E的对称点E、G，然后分别以E、G为圆心，AB、CB为半径作弧，两弧交于点F。

则△EFG就是所求。

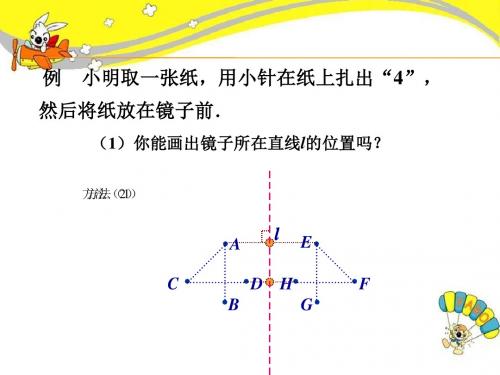
二、确定对称点例2、如图，四边形ABCD和四边形EFGH关于直线MN对称，连接AC 与BD，设它们交于点P，怎样找出点P关于MN的对称点Q？分析：找点P关于对称轴的对称点Q，有多种方法。

关键是要充分利用轴对称的性质。

解：方法一：沿直线MN对折，在点P扎孔找到对称点Q；方法二：连接FH或EG，过点P作MN的垂线，交FH于点Q，点Q即为所求；方法三：连接HG，EG交于点Q，Q就是点P关于直线MN的对称点方法四：作点P关于直线MN的对称点Q，作PO⊥MN，垂足为O，在PO 的延长线上截取OQ=OP，点Q就是点P关于直线MN的对称点。

方法五：连接FH，在FH上分别截取FQ=BP或HQ=DP，得到点Q，则点Q即为所求；三、确定对称轴例3、如图，△EFG与△ABC关于某直线成轴对称，请用不同的方法确定对称轴。

分析：确定对称轴的关键是利用对称轴是对称点连线的垂直平分线和对应边（或延长线的交点）在对称轴上。

解：方法一：连接对称点C、G与对称点A、E，再取CG、AE的中点M、N，直线MN就是所求的对称轴；方法二：连接对称点C、G，再作CG的中垂线MN，直线MN就是所求的对称轴；方法三：连接对称点C、G，再分别延长BC、FG交于M，过M作CG的垂线MN，直线MN就是所求的对称轴。

轴对称作图及实际应用（习题）例题示范例1：如图，∠AOB =60°，点P 在∠AOB 的平分线上，OP =10 cm ，点E ，F 分别是∠AOB 两边OA ，OB 上的动点，当△PEF 的周长最小时，点P 到EF 的距离是________． 【思路分析】此题求解应分为两步：① 找出△PEF 的周长最小时E ，F 的位置； ② 求出点P 到EF 的距离． 结合题目条件：特征：有定点（点P ），有动点（点E ，F ），动点在定直线OA ，OB 上运动，满足△PEF 的周长最小，判断这是轴对称最值问题．操作方法：作定点关于定直线的对称点，分别作点P 关于直线OA ，OB 的对称点P ′和P ′′，折转直，利用两点之间，线段最短，找到当△PEF 的周长最小时E ，F 的位置，进而求解． 如图1：P''P'CNM AOB EFPPF EBOAM N CP'图1 图2 如图2，连接OP ′，OP ′′， ∵∠AOB =60°，OP 平分∠AOB ， ∴∠AOP =∠BOP =30°，由轴对称性质可知OP =OP ′，OP =OP ′′，∠AOP ′=∠AOP =30°， ∠BOP ′′=∠BOP =30°，∴OP ′=OP ′′，∠POP ′=∠POP ′′=60°， ∴OP 平分∠P ′OP ′′， ∴OP ⊥P ′P ′′∴点P 到EF 的距离为线段PC 的长． 在△POP ′中，∠POP ′=60°，OP =OP ′P FEBA∴△POP ′是等边三角形 又∵OP ⊥P ′P ′′，OP =10 ∴152P C O P ==巩固练习1. 作已知线段的中点．已知：线段MN ．求作：MN 上一点O ，使OM =ON ．NM作法：（1）分别以_______，_______为圆心，__________为半径作弧，两弧相交于_______和________； （2）___________________________________． ___________________________．2. 已知△ABC ，利用直尺和圆规，根据下列要求作图（不写作法，保留作图痕迹），并填空：（1）作∠ABC 的平分线BD 交AC 于点D ；（2）作线段BD 的垂直平分线交AB 于点E ，交BC 于点F ，交BD 于点O ．由（1），（2）可得：线段EF 与线段OE 的数量关系为______________，并证明．3. 如图，已知∠AOB 的大小为α，P 是∠AOB 内部的一个定点，且OP =2，点E ，F 分别是OA ，OB 上的动点，若△PEF 周长的最小值等于2，则α=________．AB CP FEBA4. 如图，在四边形ABCD 中，∠BAD =120°，∠B =∠D =90°，在BC ，CD 上分别找一点M ，N ．当△AMN 的周长最小时，∠AMN +∠ANM =_________°．ABC DNMD C B A5. 如图，一牧童在A 处放牛，其家在B 处，A ，B 到河岸的距离分别为AC ，BD ，且AC =BD ，已知A 到河岸CD 的中点的距离为500米．牧童从A 处把牛牵到河边饮水后再回家，请作图说明牧童怎样走路程最短，并求出最短路程．思考小结1. 轴对称最值问题的特征及操作D C B A2.如图，在直线l上找一点P，使得在直线同侧的点A，B到点P的距离之和AP+BP最小，并说明理由．BAl思路提示：在l上任取一点P′（P′不与P重合），则AP+BP_____AP′+BP′（填“>”、“<”或“=”）理由如下：①由对称得：AP=_____，AP′=_____；②AP+BP=________=________，AP′+BP′=________；③由_______________________可得AP+BP_____AP′+BP′．【参考答案】1.图略（1）点M，点N，大于1M N长，点A，点B2（2）连接AB交MN于点O点O即为所求2.图略，EF=2OE；证明略3.30°4.∠AMN+∠ANM=120°5.图略，最短路程为1 000米思考小结1. 动点动和最小定点，定直线交点2. ＜①'A P，''A P②'A P+BP=AB；''B PA P+'③三角形两边之和大于第三边，＜。

四年级下册数学一课一练- 7.1轴对称一、单选题1.下面的轴对称图形是从哪张纸上剪下来的？( )A. B. C.2.三角形中是轴对称图形的是（）。

A. 所有三角形B. 等腰三角形C. 等边三角形和等腰三角形3.下列图形中，是轴对称图形的是( )。

A. B. C. D.4.如图：这个图形和下面( )图形能成轴对称．A. B. C. D.5.下列几种图形中，一定是轴对称图形的是（）。

A. 三角形B. 四边形C. 正方形D. 梯形二、判断题6.两个图形如果能完全重合，它们就是轴对称图形。

（）7.对称轴两侧的部分不能完全重合。

（）8.平行四边形可画出两条对称轴（）9.从的侧面看到的图形是轴对称图形。

（）10.平行四边形是轴对称图形．（）三、填空题11.26个英文字母中，近似轴对称图形的有很多，请试着写出3个：________，________，________。

12.下面的图案是轴对称图形的填“T”，不是的填“F”．________________________13.常见的图形线段、三角形、等腰三角形、平行四边形、梯形、圆、正方形、长方形中是轴对称图形的是________、________、________、________、________。

14.正方形有________条对称轴．15.你认识下面的汽车标志吗？按要求填一填。

(填序号)是轴对称图形的有：________不是轴对称图形的有：________四、解答题16.在方格纸上画出下面图形的轴对称图形．17.判断下列图形是否是轴对称图形，是的在( )里画“√”，不是的画“×”。

并画出是轴对称图形的所有对称轴。

五、综合题18.按要求画图。

（1）画出图形①的另一半，使它成为一个轴对称图形。

（2）先将图形②绕点O按顺时针方向旋转，再向左平移3格，分别画出旋转和平移后的图形。

（3）画出图形③按2：1扩大后的图形。

参考答案一、单选题1.【答案】C【解析】【解答】解：根据图形的特征可知，这个图形是从C图纸上剪下来的。