11_1对弧长曲线积分

第十章曲线积分与曲面积分 第一节 对弧长的曲线积分一．对弧长的曲线积分的概念 1．引入平面曲线构件L 的线密度ρ是常数，则平面曲线L 的质量为L M ρ=平面曲线构件L 的线密度ρ非均匀的，即ρ是非常数，却是曲线构件L 上点的函数),(y x f =ρ，则平面曲线构件L 质量的计算是把曲线弧L 分成n 个小段:n s s s ∆∆∆,,,21 ，其中i s ∆也表示第i 段小弧的长（0≥i s ）。

在小段弧i s ∆上任意取一点),(i i ηξ，则该小段弧的质量近似为i i i s f ∆),(ηξ曲线构件L 的质量近似为∑=→∆ni i i i s f 1),(lim ηξλ那么，曲线构件L 的质量为∑=→∆=ni i i i s f M 1),(lim ηξλ其中}{max 1i ni s ∆=≤≤λ2．对弧长的曲线积分的概念定义 设定义在平面曲线L 上的有界函数),(y x f ，将曲线弧L 任意分割成n 小段弧i s ∆，且并以i s ∆表示第i 段小弧的长，在每小段弧i s ∆上任意取一点),(i i ηξ，作和式∑=∆ni iiisf 1),(ηξ当最大小段弧的长趋于零时，和式的极限存在∑=→∆ni i i i s f 1),(lim ηξλ则此极限值称为函数),(y x f 在平面曲线L 上对弧长的曲线积分（或称为第一类曲线积分）。

记作⎰Lds y x f ),(∑=→∆=ni i i i s f 1),(lim ηξλ其中}{max 1i ni s ∆=≤≤λ，),(y x f 叫做被积函数，ds y x f ),(叫做被积表达式，ds 称为弧微分，L 称为积分路径。

如果L 是封闭曲线，则曲线积分记为⎰Lds y x f ),(3．对弧长的曲线积分的性质 对弧长的曲线积分与积分路径无关，即⎰⎰=BAABds y x f ds y x f 弧弧),(),(。

由于对弧长的曲线积分的定义与定积分、重积分的定义类似，因此也有与它们相类似的性质。

第十一章 曲线积分与曲面积分习题 11-11.设在xOy 面内有一分布着质量的曲线弧L ，在点（x,y ）处它的线密度为μ（x,y ）。

用对弧长的曲线积分分别表达：（1）这曲线弧对x 轴,对y 轴的转动惯量x I ,y I（2）这曲线弧的质心坐标x ,y2.利用对弧长的曲线积分的定义证明性质33.计算下列对弧长的曲线积分： （1）22(x y )nLds +⎰，其中L 为圆周x cos t,y sin (0t 2)a a t π==≤≤（2）(x y)ds L+⎰，其中L 为连接（1,0）及（0,1）两点的直线段（3）x Lds ⎰，其中L 为由直线y=x 及抛物线2y x =所围成的区域的整个边界 （4）22x y Leds +⎰，其中L 为圆周222x y a +=，直线y=x 及x 轴在第一象限内所围成的扇形的整个边界（5）2221ds x y z Γ++⎰，其中Γ为曲线cos ,sin ,t t tx e t y e t z e ===上相应于t 从0变到2的这段弧 （6）2x yzds Γ⎰，其中Γ为折线ABCD ，这里A,B,C,D 依次为点（0,0,0），（0,0,2），（1,0,2），（1,3,2） （7）2Ly ds ⎰，，其中L 为摆线的一拱(t sin ),y (1cos )(0t 2)x a t a t π=-=-≤≤（8）22(x )ds Ly +⎰，其中L 为曲线(cos sin ),y (sin cos )(0t 2)x a t t t a t t t π=+=-≤≤4.求半径为ａ，中心角为2ϕ的均匀圆弧（线密度1μ=）的质心5.设螺旋形弹簧一圈的方程为cos ,sin ,x a t y a t z kt ===，其中02t π≤≤，它的线密度222(x,y,z)x y z ρ=++．求： （１）它关于ｚ轴的转动惯量z I（２）它的质心。

习题 11-21.设L 为xOy 面内直线x a =上的一段，证明：(x,y)dx 0LP =⎰2.设L 为xOy 面内x 轴上从点（a,0）到点（b,0）的一段直线，证明：(x,y)dx (x,0)dxbLaP P =⎰⎰3.计算下列对坐标的积分： （1）22(xy )Ldx-⎰，其中L 是抛物线2y x =上从点（0,0）到点（2,4）的一段弧（2）Lxydx⎰，其中L 为圆周222(x )a a y a -+=（>0）及x 轴所围成的在第一象限内的区域的整个边界（按逆时针方向绕行） （3）Lydx xdy+⎰，其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到2π的一段弧（4）22(x y)dx (x y)dy L x y +--+⎰，其中L 为圆周222+y x a =（按逆时针方向绕行） （5）2x dx zdy ydzΓ+-⎰，其中Γ为曲线cos ,sin x k y a z a θ,θθ===上对应θ从0到π的一段弧 （6）(x y 1)dz xdx ydy Γ+++-⎰，其中Γ是从点（1,1,1）到点（2,3,4）的一段直线（7）+y dx dy dzΓ-⎰，其中Γ为有向闭折线ABCD ，这里的A,B,C 依次为点(1,0,0),(0,1,0),(0,0,1) （8）22(x2xy)dx (y 2xy)dyL-+-⎰，其中L 是抛物线2y x =上从点（-1,1）到点（1,1）的一段弧 4.计算(x y)dx (y x)dy L++-⎰，其中L 是：（1）抛物线2y x =上从点（1,1）到点（4,2）的一段弧（2）从点（1,1）到点（4,2）的直线段（3）先沿直线从点（1,1）到点（1,2），然后再沿直线到点（4,2）的折线（4）曲线2221,1x t t y t =++=+上从点（1,1）到点（4,2）的一段弧 5.一力场由沿横轴正方向的恒力F 所构成，试求当一质量为m 的质点沿圆周222x y R +=按逆时针方向移过位于第一象限的那一段弧时场力所做的功6.设z 轴与动力的方向一致，求质量为m 的质点从位置（x,y,z ）沿直线移到（x,y,z ）时重力所做的功7.把对坐标的曲线积分(x,y)dx Q(x,y)dyLP +⎰化成对弧长的积分曲线，其中L 为：（1）在xOy 面内沿直线从点（0,0）到点（1,1）（2）沿抛物线2y x =从点（0,0）到点（1,1）（3）沿上半圆周222x y x +=从点（0,0）到点（1,1） 8.设Γ为曲线23,,x t y t z t ===上相应于t 从0变到1的曲线弧，把对坐标的曲线积分Pdx Qdy RdzΓ++⎰化成对弧长的曲线积分习题 11-31.计算下列曲线积分，并验证格林公式的正确性： （1）22(2xy x )dx (x y )dyL-++⎰，其中L 是由抛物线2y x =和2y x =所围成的区域的正向边界曲线 （2）222(x xy )dx (y 2xy)dyL-+-⎰，其中L 是四个顶点分别为（0,0），（2,0），（2,2），（0,2）的正方形区域的正想边界2.利用曲线积分，求下列曲线所围成的图形的面积 （1）星形线33cos ,sin x a t y a t ==（2）椭圆229+16y 144x = （3）圆222x y ax +=3.计算曲线积分22ydx 2(x y )L xdy -+⎰，其中L 为圆周22(x 1)2y -+=，L 的方向为逆时针方向4.证明下列曲线积分在整个xOy 面内与路径无关，并计算积分值（1）(2,3)(1,1)(x y)dx (x y)dy++-⎰（2）(3,4)2322(1,2)(6xy y )dx (63)dy x y xy -+-⎰（3）(2,1)423(1,0)(2xy y 3)dx (x 4xy )dy-++-⎰5.利用格林公式，计算下列曲线积分： （1）(2x y 4)dx (5y 3x 6)dyL-+++-⎰，其中L 为三顶点分别为（0,0），（3,0）和（3,2）的三角形正向边界；（2）222(cos 2sin )(x sinx 2ye )dyx x Lx y x xy x y e dx +-+-⎰，其中L 为正向星形线222333(a 0)x y a +=>（3）3222(2xy y cosx)(12ysinx 3x y )dyLdx -+-+⎰，其中L 为在抛物线22x y π=上由点（0,0）到（2π，1）的一段弧（4）22(xy)dx (x sin y)dyL--+⎰，其中L 是在圆周22y x x =-上由点（0,0）到点（1,1）的一段弧6.验证下列(x,y)dx (x,y)dy P Q +在整个xOy 平面内是某一函数u(x,y)的全微分，并求这样的一个u(x,y)：（1）(2)(2)x y dx x y dy +++（2）22xydx x dy + （3）4sin sin3cos 3cos3cos 2x y xdx y xdy -（4）2232(38)(812)y x y xy dx x x y ye dy ++++ （5）22(2cos cos )(2sin sin )x y y x dx y x x y dy ++- 7.设有一变力在坐标轴上的投影为2,28X x y Y xy =+=-，这变力确定了一个力场。

弧长曲线积分公式是用于计算曲线弧长的公式。

对于参数方程表示的曲线，其弧长可以通过积分来计算。

具体的弧长曲线积分公式如下：
设曲线的参数方程为x = f(t)，y = g(t)，a ≤t ≤b，则曲线的弧长可以表示为：
L = ∫[a, b] √[f'(t)²+ g'(t)²] dt
其中，f'(t) 和g'(t) 分别表示参数方程x = f(t) 和y = g(t) 的导数。

该公式的思想是将曲线划分成无穷小的线段，然后对每个线段的长度进行求和，最终得到整个曲线的弧长。

需要注意的是，当曲线的参数方程难以直接求导时，可能需要使用其他方法来计算弧长，例如使用数值积分或近似计算方法。

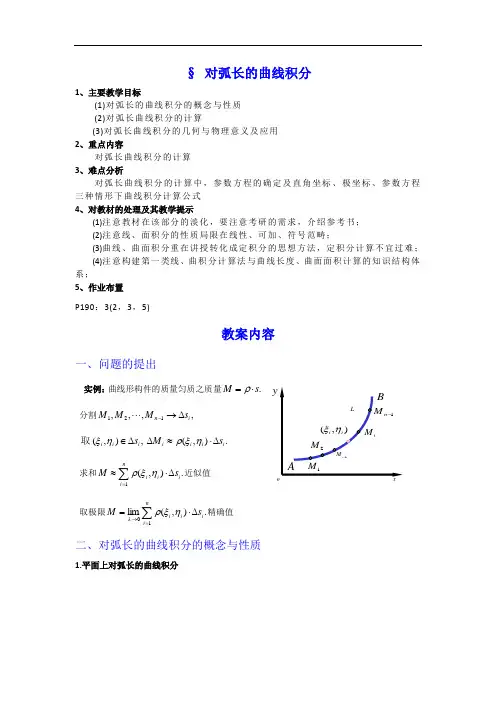
§ 对弧长的曲线积分1、主要教学目标(1)对弧长的曲线积分的概念与性质 (2)对弧长曲线积分的计算(3)对弧长曲线积分的几何与物理意义及应用 2、重点内容对弧长曲线积分的计算 3、难点分析对弧长曲线积分的计算中，参数方程的确定及直角坐标、极坐标、参数方程三种情形下曲线积分计算公式 4、对教材的处理及其教学提示(1)注意教材在该部分的淡化，要注意考研的需求，介绍参考书； (2)注意线、面积分的性质局限在线性、可加、符号范畴；(3)曲线、曲面积分重在讲授转化成定积分的思想方法，定积分计算不宜过难； (4)注意构建第一类线、曲积分计算法与曲线长度、曲面面积计算的知识结构体系；5、作业布置 P190：3(2，3，5)教案内容一、问题的提出实例：曲线形构件的质量匀质之质量.s M ⋅=ρ 分割,,,,121i n s M M M ∆→-,),(i i i s ∆∈ηξ取.),(i i i i s M ∆⋅≈∆ηξρ求和.),(1∑=∆⋅≈ni i i i s M ηξρ近似值取极限.),(lim1∑=→∆⋅=ni iiis M ηξρλ精确值二、对弧长的曲线积分的概念与性质1.平面上对弧长的曲线积分y上对弧长的曲线积分在曲线弧则称此极限为函数这和的极限存在时长度的最大值如果当各小弧段的并作和作乘积点个小段上任意取定的一为第又个小段的长度为设第个小段分成把上有界在函数面内一条光滑曲线弧为设L y x f s f s f i s i n L L y x f xoy L ni i i i i i i i i i ),(,,0,),(,),(,),(,..),(,1→∆⋅∆⋅∆∑=ληξηξηξ.),(lim ),(,),(1∑⎰⎰=→∆⋅=ni i i i LL s f ds y x f ds y x f ηξλ即记作2.空间中对弧长的曲线积分上对弧长的曲线积分为在空间曲线弧函数Γ),,(z y x f.),,(lim ),,(1i ni i i i s f ds z y x f ∆⋅=∑⎰=→Γζηξλ3.曲线积分的存在性.),(,),(存在对弧长的曲线积分上连续时在光滑曲线弧当⎰L ds y x f L y x f4.分段光滑的曲线上对坐标的曲线积分)(,)(21L L L L +=Γ是分段光滑的或若.),(),(),(2121⎰⎰⎰+=+L L L L ds y x f ds y x f ds y x f5.闭曲线积分.),(),(⎰Lds y x f L y x f 为上对弧长的曲线积分记在闭曲线函数 6.对弧长的曲线积分的性质.),(),()],(),([)1(⎰⎰⎰±=±LLLds y x g ds y x f ds y x g y x f).(),(),()2(为常数k ds y x f k ds y x kf LL⎰⎰=.),(),(),()3(21⎰⎰⎰+=L L Lds y x f ds y x f ds y x f ).(21L L L +=三、对弧长的曲线积分的计算法1.定理(计算曲线积分的公式)的参数方程为上有定义且连续在曲线弧设L L y x f ,),())((),(βαψϕ≤≤==t t y t x)()()()](),([),(,],[)(),(22βαψϕψϕβαψϕβα<'+'=⎰⎰dt t t t t f ds y x f t t L则上具有一阶连续导数在其中例1 ).(,sin ,cos :,象限第椭圆求I ⎩⎨⎧===⎰t b y t a x L xyds I L解答要点：dt t b t a t b t a I 2220)cos ()sin (sin cos +-⋅=⎰πdt t b t a t t ab 222220cos sin cos sin +=⎰π⎰-=ab du u b a ab 222)cos sin (2222t b t a u +=令.)(3)(22b a b ab a ab +++=2.其它计算公式.)(:)1(b x a x y L ≤≤=ψ.)(1)](,[),(2dx x x x f ds y x f baL⎰⎰'+=ψψ)(b a <.)(:)2(d y c y x L ≤≤=ϕ.)(1]),([),(2dy y y y f ds y x f dcL⎰⎰'+=ϕϕ)(d c <)().(),(),(:)3(βαωψϕ≤≤===Γt t z t y t x)()()()()](),(),([),,(222βαωψϕωψϕβα<'+'+'=⎰⎰Γdt t t t t t t f ds z y x f3.应注意的问题;.1βα一定要小于上限定积分的下限.,,),(.2而是相互有关的不彼此独立中y x y x f例2 .)2,1()2,1(,4:,2一段到从其中求-==⎰x y L yds I L解答要点：dy y y I 222)2(1+=⎰-.0= 例3 ⎰Γ=xyzds I 求，其中)20(,sin ,cos :πθθθθ≤≤===Γk z a y a x解答要点：⎰+⋅=πθθθθ20222sin cos d k a k a I .21222k a ka +-=π例4 ⎩⎨⎧=++=++Γ=⎰Γ.0,,22222z y x a z y x ds x I 为圆周其中求解答要点：由对称性, 知.222⎰⎰⎰ΓΓΓ==ds z ds y ds xxy 42=⎰Γ++=ds z y x I )(31222故⎰Γ=ds a 32.323a π=),2(球面大圆周长⎰Γ=ds a π例5 计算曲线积分dsz y x )(222++⎰Γ 其中为螺旋线x a cos t 、y a sin t 、z kt 上相应于t 从0到达2的一段弧解 在曲线上有x 2y 2z 2(a cos t )2(a sin t )2(k t )2a 2k 2t 2 并且 dt k a dt k t a t a ds 22222)cos ()sin (+=++-=于是ds z y x )(222++⎰Γ⎰++=π2022222)(dt k a t k a)43(3222222k a k a ππ++=四、几何与物理意义,),()1(的线密度时表示当L y x ρ;),(⎰=Lds y x M ρ;,1),()2(⎰=≡Lds L y x f 弧长时当,),(),()3(处的高时在点上的柱面表示立于当y x L y x f.),(⎰=Lds y x f S 柱面面积,)4(轴的转动惯量轴及曲线弧对y x .,22⎰⎰==Ly L x ds y I ds x I ρρ曲线弧的重心坐标)5(.,⎰⎰⎰⎰==LL L L dsds y y dsds x x ρρρρ 五、小结1、对弧长曲线积分的概念2、对弧长曲线积分的计算3、对弧长曲线积分的应用sL。

对弧长的曲线积分和对坐标的曲线积分
对弧长的曲线积分和对坐标的曲线积分是两种不同的积分方法，它们有不同的积分公式和不同的应用场景。

1. 对弧长的曲线积分：
对弧长的曲线积分也被称为第一类曲线积分，它是对弧长进行积分的一种方法。

这种积分方法可以求得曲线段上变力所做的功。

在这种方法中，我们假设线段在每一点的线密度为
f(x,y)，那么在这段线段上任意一点的附近取一个微小弧长ds，则有ds与dx、dy满足勾股定理。

在这种情况下，我们可以将
力F分解为两个分量，即沿着x轴的分力和沿着y轴的分力，它们分别记为P和Q。

这样，力F所做的功就可以分解为沿着
x轴和y轴的两个分量分别所做的功，再将它们相加即可得到
总功。

2. 对坐标的曲线积分：
对坐标的曲线积分也被称为第二类曲线积分，它是对坐标进行积分的一种方法。

这种积分方法可以求得沿着曲线段的功。

在这种方法中，我们将曲线段看作是由许多微小的线段组成的，然后对每一段微小的线段进行积分。

在线段上每一点，我们都有P=Fcosα，Q=Fcosβ，其中F是与x轴夹角为α，与y轴夹
角为β的力。

这样，我们就可以将力F分解为两个分量，即沿着x轴的分力和沿着y轴的分力，它们分别记为P和Q。

然后，我们可以将沿着x轴和y轴的两个分量分别与坐标x和y相乘，再将它们相加即可得到总功。

总之，对弧长的曲线积分和对坐标的曲线积分是两种不同的积分方法，它们有不同的积分公式和不同的应用场景。

在解决实际问题时，我们需要根据具体场景选择合适的积分方法。