第4讲对弧长的曲线积分
- 格式:ppt
- 大小:736.00 KB
- 文档页数:41


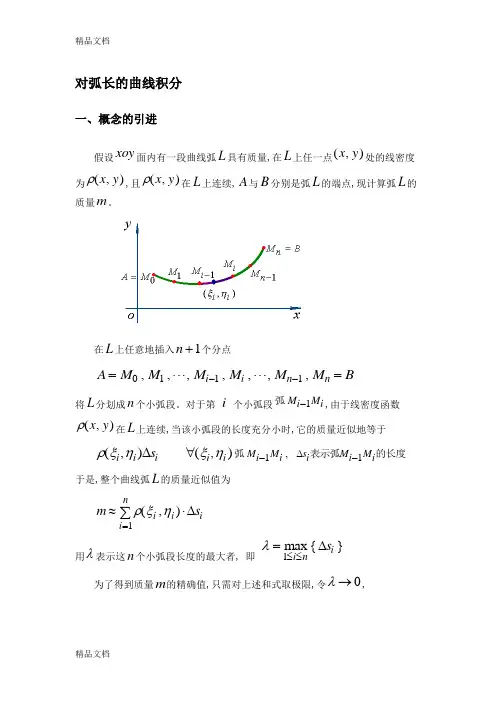
对弧长的曲线积分一、概念的引进假设xoy 面内有一段曲线弧L 具有质量,在L 上任一点(,)x y 处的线密度为ρ(,)x y ,且ρ(,)x y 在L 上连续,A 与B 分别是弧L 的端点,现计算弧L 的质量m 。
在L 上任意地插入n +1个分点A M M M M M MB i i n n ==--0111,,,,,,,将L 分划成n 个小弧段。
对于第 i 个小弧段弧M i M i -1,由于线密度函数ρ(,)x y 在L 上连续,当该小弧段的长度充分小时,它的质量近似地等于ρξηξη(,)(,),i i ii i M i M i s i M i M i s ∆∆∀--弧表示弧的长度11于是,整个曲线弧L 的质量近似值为m s i i ii n≈⋅=∑ρξη(,)∆1用λ表示这n 个小弧段长度的最大者, 即λ=≤≤max {}1i ni s ∆为了得到质量m 的精确值,只需对上述和式取极限,令λ→0,即m s i i ii n=⋅→=∑lim (,)λρξη01∆ (1)撇开上例的物理意义,我们引入对弧长的曲线积分的概念。
【定义】设L 为xoy 面内的一条光滑曲线弧,函数f x y (,)在L 上有界,在L 内任意地插入n +1点,A M M M M M MB i i n n ==--0111,,,,,,,它把L 分成n 个小弧段,设第i 个小段弧M i M i -1的长度为∆s i ,(,)ξηi i 为弧M i M i -1上任取的一点,记λ=≤≤max {}1i ni s ∆作和式 f s i i ii n(,)ξη⋅=∑∆1如果极限 lim (,)λξη→=⋅∑01f s i i ii n∆ 存在,这个极限值就叫做函数f x y (,)在曲线弧L 上对弧长的曲线积分,记作f x y dsL(,)⎰。
亦即 f x y ds f s L i i i i n(,)lim (,)⎰∑=⋅→=λξη01∆其中:f x y (,)叫做被积函数, L 叫做积分弧段。

弧长曲线积分公式是用于计算曲线弧长的公式。
对于参数方程表示的曲线,其弧长可以通过积分来计算。
具体的弧长曲线积分公式如下:
设曲线的参数方程为x = f(t),y = g(t),a ≤t ≤b,则曲线的弧长可以表示为:
L = ∫[a, b] √[f'(t)²+ g'(t)²] dt
其中,f'(t) 和g'(t) 分别表示参数方程x = f(t) 和y = g(t) 的导数。
该公式的思想是将曲线划分成无穷小的线段,然后对每个线段的长度进行求和,最终得到整个曲线的弧长。
需要注意的是,当曲线的参数方程难以直接求导时,可能需要使用其他方法来计算弧长,例如使用数值积分或近似计算方法。






对弧长的曲线积分公式极坐标在我们学习数学的旅程中,有一个概念叫对弧长的曲线积分公式极坐标。
这玩意儿,听起来是不是有点让人头大?别慌,让我来给您好好说道说道。
先来说说啥是曲线积分。
想象一下,有一条弯弯曲曲的线,就像公园里那种曲折的小路。
我们要沿着这条小路做一些计算,这就是曲线积分啦。
而极坐标呢,就像是给我们换了一副特别的眼镜来看世界。
咱们平常熟悉的坐标是直角坐标,就是那个横横竖竖的x 轴、y 轴。
极坐标可不一样,它用角度和距离来确定一个点的位置。
比如说,您告诉别人“我在离原点 3 米远,角度是 45 度的地方”,这就是极坐标的表达方式。
那把曲线积分和极坐标放在一块儿,就有了对弧长的曲线积分公式极坐标。
这个公式看起来挺复杂,但其实就是帮助我们在极坐标下计算沿着曲线的一些量。
我记得有一次给学生讲这个知识点的时候,有个小家伙皱着眉头问我:“老师,这东西到底有啥用啊?”我笑了笑,跟他们说:“同学们,想象一下,咱们要给一个圆形的花坛围上一圈彩灯,那得知道需要多长的彩灯线吧?这时候这个公式就能派上用场啦。
”为了让大家更好地理解,我在黑板上画了一个大大的极坐标图,标上了角度和距离。
然后一步一步地推导公式,边写边解释每个符号的含义。
那认真的劲儿,就像是在雕琢一件精美的艺术品。
同学们也跟着我的节奏,眼睛一眨不眨地盯着黑板,时不时还点点头,好像突然明白了什么。
在推导的过程中,有个平时挺调皮的学生突然喊了一句:“老师,我好像懂了!”那一瞬间,我心里别提多高兴了,就觉得所有的辛苦都值了。
当我们把这个公式弄明白之后,再去做那些相关的题目,就会发现其实也没那么难。
比如说,计算一个极坐标下的曲线长度,只要把相应的参数代入公式,认真算一算,答案就出来啦。
总之,对弧长的曲线积分公式极坐标虽然看起来有点复杂,但只要我们用心去学,多做几道题,多琢磨琢磨,就能掌握它的奥秘。
就像我们在生活中面对困难一样,只要不退缩,总能找到解决的办法。
希望大家在学习这个知识点的时候,都能充满信心,加油!。
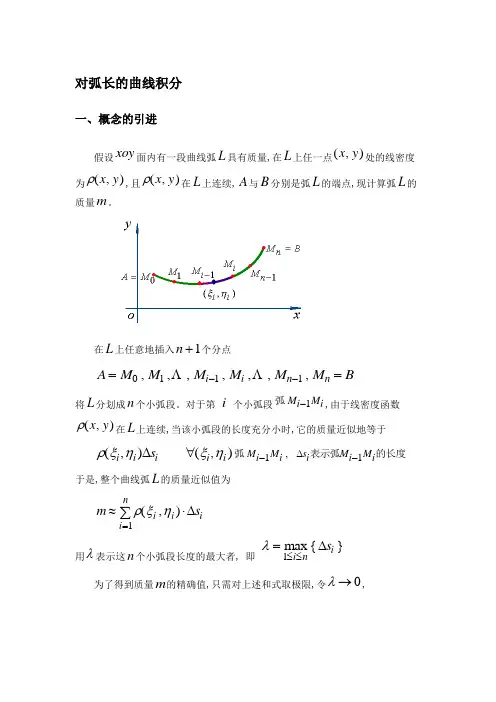
对弧长的曲线积分一、概念的引进假设xoy 面内有一段曲线弧L 具有质量,在L 上任一点(,)x y 处的线密度为ρ(,)x y ,且ρ(,)x y 在L 上连续,A 与B 分别是弧L 的端点,现计算弧L 的质量m 。
在L 上任意地插入n +1个分点A M M M M M MB i i n n ==--0111,,,,,,,将L 分划成n 个小弧段。
对于第 i 个小弧段弧M i M i -1,由于线密度函数ρ(,)x y 在L 上连续,当该小弧段的长度充分小时,它的质量近似地等于ρξηξη(,)(,),i i ii i M i M i s i M i M i s ∆∆∀--弧表示弧的长度11于是,整个曲线弧L 的质量近似值为m s i i ii n≈⋅=∑ρξη(,)∆1用λ表示这n 个小弧段长度的最大者, 即λ=≤≤max {}1i ni s ∆为了得到质量m 的精确值,只需对上述和式取极限,令λ→0,即m s i i ii n=⋅→=∑lim (,)λρξη01∆ (1)撇开上例的物理意义,我们引入对弧长的曲线积分的概念。
【定义】设L 为xoy 面内的一条光滑曲线弧,函数f x y (,)在L 上有界,在L 内任意地插入n +1点,A M M M M M MB i i n n ==--0111,,,,,,,它把L 分成n 个小弧段,设第i 个小段弧M i M i -1的长度为∆s i ,(,)ξηi i 为弧M i M i -1上任取的一点,记λ=≤≤max {}1i ni s ∆作和式 f s i i ii n(,)ξη⋅=∑∆1如果极限 lim (,)λξη→=⋅∑01f s i i ii n∆ 存在,这个极限值就叫做函数f x y (,)在曲线弧L 上对弧长的曲线积分,记作f x y dsL(,)⎰。
亦即 f x y ds f s L i i i i n(,)lim (,)⎰∑=⋅→=λξη01∆其中:f x y (,)叫做被积函数, L 叫做积分弧段。
对弧长的曲线积分计算思路、步骤与典型例题展开全文一、对弧长的曲线积分的几何意义与物理意义1、构建对弧长的曲线积分的模型对弧长的曲线积分即在微元弧微分ds分布的曲线上求分布的量的和。
比如小段ds的质量近似量,即为ds上一点(x,y,z)的线密度与弧长的乘积ρ(x,y,z)ds,总的曲线型构建的质量即为ds分布的曲线Γ上求和,从而得到对弧长的曲线积分模型描述形式为其中平面上的曲线积分即为以上模型的特殊情况,即z=0的情形。
2、对弧长的曲线积分的几何意义(1) 当f(x,y)=1时,表示积分曲线段L的长度;(2) 当f(x,y)>0时,表示以xOy面上的曲线L为准线,母线平行于z轴,顶部为(x,y,f(x,y))点构成的曲线的柱面片的面积。
当f(x,y,z)=1时,表示积分曲线段Γ的长度。
3、对弧长的曲线积分的物理意义当f(x,y)>0,f(x,y,z)>0时,分别表示平面曲线段L与空间曲线段Γ的长度。
二、对弧长的曲线积分的计算方法不管是空间曲线还是平面曲线,曲线积分的计算公式可以统一描述为其中C:r=r(t),a≤t≤b,即由曲线C的参数方程式分量构成的向量值函数描述形式,其中|r’(t)|表示向量值函数r=r(t)的导数向量的模。
1.积分曲线为平面曲线的情形● 当C:y=y(x),a≤x≤b时,则r=r(x)=(x,f(x)),a≤x≤b,所以有● 当C:x=x(x),y=y(t),a≤t≤b时,则r=r(t)=(x(t),y(t)),a≤t≤b,所以有● 当C:ρ=ρ(θ),α≤θ≤β时,则r=r(θ)=( ρ(θ)cosθ, ρ(θ)sinθ),α≤θ≤β,所以有2.积分曲线为空间曲线的情形当C:x=x(x),y=y(t),z=z(t),a≤t≤b时,则r=r(t)=(x(t),y(t), z(t)),a≤t≤b,所以有【注】|r’(t)|dt即为弧微分,弧长大于0,所以以上的定积分计算式中一定有积分下限小于积分上限。