关于maxwell v12中气隙磁密的计算

08气隙磁导计算气隙磁导计算是电机设计中的重要环节之一，其结果直接影响电机的性能和效率。

在进行具体的气隙磁导计算之前，我们需要了解一些基本概念和公式。

首先，气隙磁导是指磁场通过气隙时的磁场强度与磁场电势梯度之比。

在电机中，气隙磁导对磁通的传递起到了重要的作用，影响电机的磁路特性。

1.磁通密度(B)：磁通密度是磁力线通过截面积的数量，单位为特斯拉或高斯。

对于永磁体，磁通密度可以通过磁感应强度来计算，即B=μ0H，其中μ0为真空中的磁导率，其值为4π×10-7H/m。

3.磁通(Φ)：磁通是由磁场强度引起的磁力线的数量。

在电机中，磁通可以通过磁通密度与环境的截面积之积来计算，即Φ=B∙A，其中A为截面积。

根据上述概念，我们可以得到气隙磁导的计算公式为：Λ=Φ/(H_g-H_c)其中，Λ为气隙磁导，Φ为磁通，H_g为气隙中的磁场强度，H_c为铁芯中的场强。

需要注意的是，由于气隙是非磁性材料，所以在气隙中的磁场强度相对于铁芯较低。

在具体计算气隙磁导时，我们需要先了解电机的结构和材料。

电机主要由铁芯和气隙组成，铁芯具有高磁导率，而气隙则具有较低的磁导率。

对于简单的直流电机，我们可以将其近似看作是矩形气隙。

Λ=(l_g×μ_g)/(A_g×μ_0)其中，l_g为气隙长度，μ_g为气隙的磁导率，A_g为气隙的截面积。

在实际应用中，气隙的长度和截面积往往可以直接测量得到。

而气隙的磁导率则需要根据材料的磁导率表进行查找，然后进行合适的取值。

在计算气隙磁导时，还需要考虑不同材料之间的接触电阻。

由于接触电阻会引起能量的损失，因此需要将其考虑在内。

总之，气隙磁导计算是电机设计中一个重要且复杂的环节。

通过计算气隙磁导可以帮助我们更好地理解电机的磁路特性，从而进行合理的设计和优化。

但需要强调的是，在实际应用中，需要综合考虑各种因素，包括材料的特性、电机的结构等，在不同的设计要求下进行合理的气隙磁导计算。

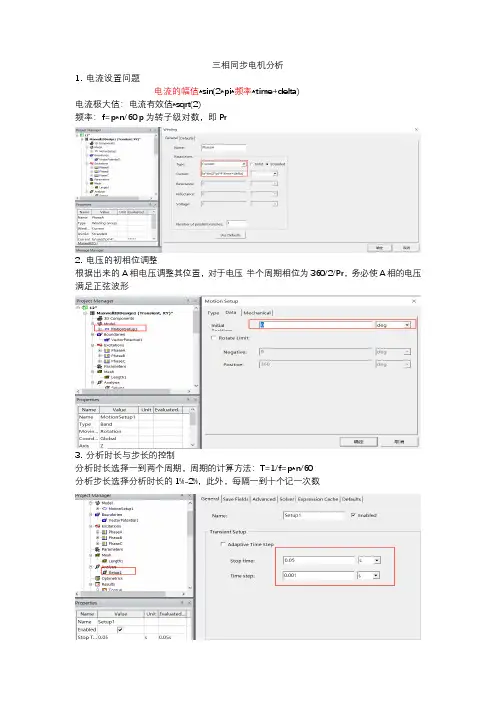
三相同步电机分析1. 电流设置问题电流的幅值*sin(2*pi*频率*time+delta)电流极大值：电流有效值*sqrt(2)频率：f=p*n/60 p为转子级对数，即Pr2. 电压的初相位调整根据出来的A相电压调整其位置，对于电压半个周期相位为360/2/Pr，务必使A相的电压满足正弦波形3. 分析时长与步长的控制分析时长选择一到两个周期，周期的计算方法：T=1/f=p*n/60分析步长选择分析时长的1%-2%，此外，每隔一到十个记一次数4. 基于坐标变换的交流磁场磁通密度的调整(-Moving1.Position -初始相位 * PI/180) * 极对数 + PI注意前面要加个负号5. 空载情况下的三个校核要点电流要为零+A相电压从零开始起步+Flux_q=0(磁通变化后)Flux-d是沿磁极正向的磁场强度，Flux-q是垂直于磁场方向的磁场强度，正常情况下，垂直于磁场方向应该为06. 删除现有的结果7. 负载要将电流初相位delta改为零，然后给电流的大小赋值8. 气隙磁密分布情况使用气隙中间的圆线作为参考面，使用场计算器计算B在中心面上的径向与切向分量在result中添加曲线可以在此处更改对应的时间9. 对气隙磁密进行傅里叶分解首先要进行坐标变化，把横坐标变成1，并且注意要用标准单位可以用鼠标划分局部显示傅里叶结果的横坐标是谐波极对数（频率），纵坐标是谐波幅值10. 网格划分问题可以通过画圆圈线手动加密气隙网格密度，画圈之后，将coverlines删除，将自动保留线画完曲线之后再画网格，并通过plotmesh查看11. 矢量场向量曲面积分计算问题在指定的曲线上，当需要插入函数的时候，先将变量以及加减乘除运算符先加上，然后使用积分函数integ 函数，需要注意的是，此处为矢量的线积分，要注意公式的转换·1，一般，极坐标积分可以提出一个r 出来，即：()r f d θθ∫在线积分时就变成了：()l f d θ∫。

磁场密度计算公式磁场密度是描述磁场强度分布的物理量，通常用磁感应强度（磁感应力线通过单位面积的数量）来表示。

磁场密度的计算公式可以通过安培环路定理和毕奥-萨伐尔定律得到。

在进行磁场密度计算之前，我们首先要了解一些基本概念。

磁场是由电流产生的，当电流通过导线或线圈时会形成一个环绕它的磁场。

磁感应强度B是描述磁场的一个重要参数，它的大小和方向可以用磁力线来表示。

磁力线是一种无形的力线，它沿着磁场的方向指示磁场的强度和方向。

根据安培环路定理，通过一个放置在磁场中的闭合回路所围成的面积S，磁感应强度B的总磁通量ΦB等于该回路上的电流I穿过该回路的次数的乘积。

这个定理可以用公式表示为ΦB = B * S = ∫B·dS，其中∫表示对闭合回路上的面积分，B·dS表示磁感应强度在该面积上的投影。

我们还可以利用毕奥-萨伐尔定律来计算磁场密度。

根据这个定律，任何一个点的磁感应强度B，都等于由该点引起的磁场在该点的磁感应强度对该点的矢量和。

这个定律也可以用公式表示为B =∫(μ0/(4π)) * (I * dl × r) / r^3，其中∫表示对整个回路的线积分，I表示电流，dl表示回路上的微小线段，r表示从线段指向观察点的位矢，μ0表示真空中的磁导率，其值约为4π × 10^-7 T·m/A。

通过以上公式，我们可以计算出磁场密度的数值。

但需要注意的是，这些公式适用于理想情况，即导线或回路是细长无限长的理想导体，且磁场的源是准静态的。

在实际应用中，如果导线或线圈的形状复杂，或者存在非理想的情况（如电流变化较快），我们可能需要借助数值计算或辅助工具来进行更精确的计算。

磁场密度的计算是磁场研究中的基础问题，对于理解磁场的分布规律和应用具有重要意义。

通过计算磁场密度，我们可以更好地设计和优化磁场配置，提高各种磁场设备的性能，满足不同应用领域的需求。

磁场密度的计算还可以帮助我们研究磁场的相互作用规律，探索更多磁场应用的可能性。

第54卷第3期2021年3月Vol.54.No.3Mae2021微电机MICROMOTORS直线电机不均匀气隙磁场解析计算方法刘思嘉，刘子锐(北京信息科技大学化学院，北京100192)摘要：直线感应电机运行时，其初级和次级之间可能因不平行而形成不均匀气隙，从而造成电机磁场分布变化。

对于这种不均匀气隙的电机磁场分布的计算，沿用 的基于均匀气隙的公式则会大。

为问题，首先基于电磁论，提出了一种不均匀气隙直线感应电机磁场的解析计算公式；其次线电机对解析公式进行；最后将解析公式计算结果与有限元方法计算得到的气隙磁场分布结果进行了对比％对比结果表明，这种 了气隙不均匀的解析磁场计算方法相气隙不均匀的计算，其平均小50%以上，为直线感应电机的设计和控制效果的提升提供了一种有益的％关键词：直线感应电机；不均匀气隙；磁析计算；有限元中图分类号：TM359.4文献标志码：A文章编号：1001-6848(2021)03-0041-05An Analytical Calculation Method of Flux Density for Uneven Air-gapLinear Induction MotorLIUSojoa，LIU Zoeu o(School of Automation,，Beijing Information of Science&Technology Unnersity，Beijing100192，China)Abstract:The linear induction motor(LIM)may lead to an uneven air-cap bWwwn its pamda and second-o/duang operation.This uneven air-cap will bring the vvriation of flux distribution in the LIM.The tradi­tional calculation method for electric machine flux will enhanco ewor when not consideang the uneven air­gap.Aiming to this problem，this paper firstly presented an analytic calculating metOod of the flux density based on MaxwWl's th—a，secondly provided a correction method consideang the uniqueness of LIM，final­ly compared Oie results with the results of th/inite element mwliod(FEM).The compaason Olustrates that the analytic method reduces the calculation wroe over50%Oian the calculation without consideang the une­ven air-cap.This method provides a useful afeanco for the future design and conOol of LIMs.Key wo—t:linear induction motor；uneven air-cap；analytical lux calculation；finite element methodo引言长期以来，直线感应电机(Linear Induction Mo-tvr，LIM)在轨道交得到大量关注，在国内外有大量的工程应用。

计及多因素影响的永磁电机空载气隙磁密解析计算法王建飞;张琪;黄苏融【摘要】为准确而快速地计算与评估电机的性能,以I型转子结构永磁电机为例,提出了一种计及多因素影响的空载气隙磁密的解析计算法,并用有限元进行了仿真验证.分析了永磁体尺寸、隔磁桥高度和极弧系数等参数对气隙磁密的影响规律,为优化电机方案提供了思路.【期刊名称】《电机与控制应用》【年(卷),期】2018(045)008【总页数】6页(P50-55)【关键词】永磁电机;多因素;气隙磁密;有限元【作者】王建飞;张琪;黄苏融【作者单位】上海大学,上海200072;上海大学,上海200072;上海大学,上海200072【正文语种】中文【中图分类】TM3510 引言永磁电机以其高效率、高功率密度、快速动态响应特性等显著优点在工业驱动和伺服控制系统等领域得到了广泛应用。

永磁电机气隙磁密波形的优劣直接影响电机的转矩品质和感应电势波形的正弦度，因此永磁电机气隙磁密的分布设计尤为关键[1-2]。

建立准确的永磁电机的气隙磁密解析计算式，有助于在电机初步设计阶段获悉气隙磁密的大小和波形，为电磁性能快速准确的分析和方案的评估提供有效的途径。

气隙磁密可以由不同的方法获得(如解析计算法、有限元法或者磁路法)。

解析计算法通常忽略了铁心饱和、齿槽效应及漏磁的影响[3-5]。

有限元法建立了精确的电机模型，计算精度与剖分密度有关，电机模型剖分越细，精确度越高，计算时间越长[6-7]。

磁网络法通常能考虑铁心饱和，但忽略了齿槽效应的影响[8-10]。

为了弥补传统解析计算法存在的缺陷，本文提出一种计及多因素影响的永磁电机空载气隙磁密的解析计算法，能有效地考虑铁心饱和、齿槽效应和极间漏磁对空载气隙磁密的影响。

基于导出的解析计算式分析了永磁体尺寸、隔磁桥高度和极弧系数等参数对气隙磁密分布的影响规律，并将解析计算的气隙磁密波形与有限元仿真结果进行比较。

1 计及多因素影响的永磁电机空载气隙磁密解析计算式本文以1台48槽8极内置式永磁同步电机为例进行分析。

方法一：
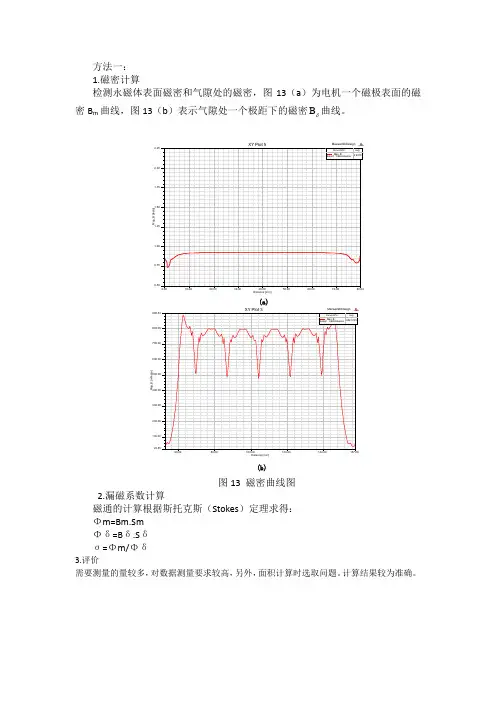
1.磁密计算
检测永磁体表面磁密和气隙处的磁密，图13（a）为电机一个磁极表面的磁
曲线。

密B m曲线，图13（b）表示气隙处一个极距下的磁密B
(b)
图13 磁密曲线图
2.漏磁系数计算
磁通的计算根据斯托克斯（Stokes）定理求得：
Φm=Bm.Sm
Φδ=Bδ.Sδ
σ=Φm/Φδ
3.评价
需要测量的量较多，对数据测量要求较高，另外，面积计算时选取问题。

计算结果较为准确。

方法二：
1.数磁力线。

磁极发出的总磁力线数目减掉漏掉的就是通过电枢的。

2.这种方法快，简便，比较准确。

方法三：
1.直接检测磁体表面的一个点处磁密作为Bm，和电枢处一个点的磁密作为Bδ.
2.相比较前两种，这种方法没考虑面积，误差还是较大的。

内置式永磁电机漏磁系数直观认识：
工作磁密小，电枢内径小，气隙大，磁桥越大，漏磁系数越大。

基于Ansoft Maxwell 的电机气隙径向磁密求取
编写：y1949b
日期：2011-7-10
首发：西莫论坛（）
1 前言
使用工具： Ansoft Maxwell 2D V14.0
目的：求取电机气隙径向磁密
例子：pmsg-1.mxwl
例子所在目录：C:\Program Files\Ansoft\Maxwell14.0\Examples\RMxprt\pmsg（默认安装路径的话）
2 正文
使用静磁场求解器，本例求解的为永磁同步电机的空载气隙径向磁密，电机模型如图2-1，为全模型。

图2-1
打开场计算器，如图2-2所示
图2-2
场计算器如图2-3所示，其中序号1、2、3、4、5 为主要的点取顺序，其气隙径向磁密利用的公式2-1为
B=B X×cos(θ)+ B Y×sin(θ) （2-1）式中 B-径向磁密
B X-磁密的x轴分量
By-磁密的y轴分量
θ-柱坐标的θ
图2-3
具体的点取顺序见下图2-4至2-13
图2-4
图2-5
图2-6
图2-6
图2-7
图2-8
图2-9
图2-10
图2-11。

2010年第43卷第8期双转子径向永磁电机气隙磁密的分析计算收稿日期:2009 07 21基金项目:广州市科技计划项目(2008Z1-D421曹江华,杨向宇,肖如晶(华南理工大学电力学院,广州 510640摘要:双转子径向永磁电机可以大大提高转矩密度和效率。

该文首先简要介绍了双转子径向永磁电机的基本结构、原理、特性及设计依据,然后采用等效磁路法对气隙磁密进行了解析,最后利用有限元法对所设计电机进行了静态磁场的分析和气隙磁密计算值的验证。

结果表明,双转子径向永磁电机在磁场上可看作由共用定子铁心的两个传统内、外转子永磁电机并联而成,气隙磁密的解析值和有限元计算值也吻合得较好,证明了分析和设计的可行性。

关键词:双转子径向永磁电机;气隙磁密计算;静态磁场;有限元分析中图分类号:TM 351 文献标志码:A 文章编号:1001 6848(201008 0028 03Calculation of Airgap F lux D ensity in Dual rotor Radial fluxPerm anentM agnetM achinesC AO Jiang hua ,YANG X iang yu,X IAO Ru ji n g(Co llege of E lectric Po w er ,South China University o f T echno logy,Guangzhou 510640,China Abst ract :Dual rotor radial fl u x per m anent m agnet m ach i n es can substantially i m prove the torque densityand effic i e ncy .This paper briefly intr oduced its basi c str ucture ,operati o n pri n ciple ,characteristics and desi g n basis ,calcu lated t h e a ir gap flux density based on t h e equ i v a lent m agnetic c ircu i.t I n additi o n ,to analyze the m agnetostatic fi e l d and prove the effectiveness o f t h e ca lculated flux density w ith the fi n ite e le m ent m ethod .The resu lts sho w that the m agnetic fie l d o f dual roto r rad ial flux per m anent m agnet m achines can be regarded as a parallel co m b i n ation o f t w o traditi o na l inner and outer per m anent m agnet m achines shared a co mm on stator core and the airgap flux density values ca lculated by the analytic and fi n ite ele m ent m ethod m atch w el,l w hich verifies the feasi b ility o f the analysis and design .K ey W ords :Dual rotor radia l flux per m anent m agnet m achines ;C alcu lation of a irgap flux density ;M ag netostatic field ;F i n ite ele m ent analysis0 引言与单转子结构相比,采用双转子结构可以充分利用电机内部空间,克服磁拉力,减小漏磁,大大提高电机的转矩密度和效率。