常微分方程大纲(数学与应用数学专业)

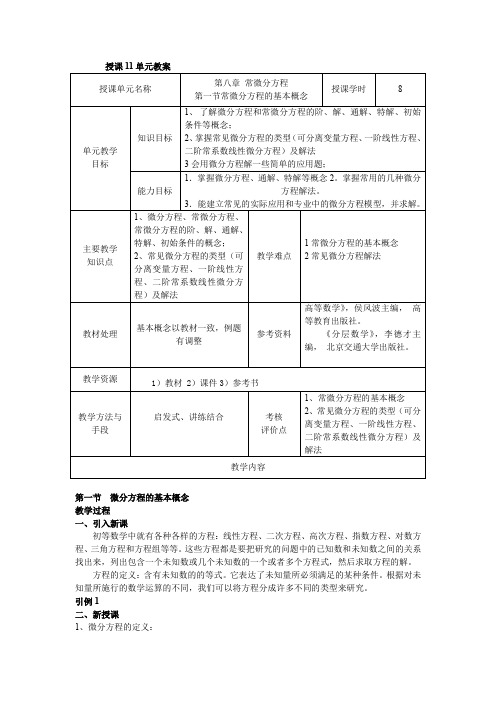
授课11单元教案第一节微分方程的基本概念教学过程一、引入新课初等数学中就有各种各样的方程：线性方程、二次方程、高次方程、指数方程、对数方程、三角方程和方程组等等。

这些方程都是要把研究的问题中的已知数和未知数之间的关系找出来，列出包含一个未知数或几个未知数的一个或者多个方程式，然后求取方程的解。

方程的定义：含有未知数的的等式。

它表达了未知量所必须满足的某种条件。

根据对未知量所施行的数学运算的不同，我们可以将方程分成许多不同的类型来研究。

引例1二、新授课1、微分方程的定义：含有未知函数的导数或微分的方程，称为微分方程如果未知函数是一元函数的微分方程称为常微分方程式；如果未知函数是多元函数的微分方程式称为偏微分方程。

例如，22;d yx y x dx=+=dx 和是常微分方程dyzxy x∂=∂是偏微分方程. 微分方程中未知函数的最高阶导数的阶数，称为微分方程式的阶。

一阶微分方程的一般形式为 (,,)0F x y y '= 例如：2354()0y x y x '+-=，2()20dy dyx y x dx dx-+=都是一阶微分方程。

二阶微分方程的一般形式为 (,,,)0F x y y y '''= 例如：222sin 0d y dyyx dx dx-+=，2223()(2)y k y '''=+都是二阶微分方程。

类似可写出n 阶微分方程的一般形式 ()(,,,,)0n F x y y y y '''=。

其中F 是n +2个变量的函数。

这里必须指出，在方程()(,,,,)0n F x y y y y '''=中，()n y 必须出现，而,,,x y y '(1),n y y -''等变量可以不出现。

例如()()n y f x =也是n 阶微分方程。

例1 ．指出下列方程中哪些是微分方程，并说明它们的阶数：122222222(1) 0; (2) 2;(3) sin 0; (4) 3;(5) '''3; (6) ;(7) '''(')0. t dy y dx y y x d yxdy y xdx y e dt yy y x dy dx x y xy y -==++=+=+==+-=2、微分方程的解能够满足微分方程的函数都称为微分方程的解 求微分方程的解的过程，称为解微分方程例如，函数3x 16是微分方程22d y x dx =的解。

《常微分方程》课程大纲一、课程简介课程名称：常微分方程学时/学分：3/54先修课程：数学分析，高等代数,空间解析几何，或线性代数（行列式，矩阵与线性方程组，线性空间F n，欧氏空间R n，特征值与矩阵的对角化）, 高等数学（多元微积分，无穷级数）。

面向对象：本科二年级或以上学生教学目标：围绕基本概念与基本理论、具体求解和实际应用三条主线开展教学活动，通过该课程的教学，希望学生正确理解常微分方程的基本概念，掌握基本理论和主要方法，具有一定的解题能力和处理相关应用问题的思维方式，如定性分析解的性态和定量近似求解等思想，并希望学生初步了解常微分方程的近代发展，为学习动力系统学科的近代内容和后续课程打下基础。

二、教学内容和要求常微分方程的教学内容分为七部分，对不同的内容提出不同的教学要求。

(数字表示供参考的相应的学时数，第一个数为课堂教学时数，第二个数为习题课时数)第一章基本概念（2，0）（一）本章教学目的与要求：要求学生正确掌握微分方程，通解，线性与非线性，积分曲线，线素场（方向场），定解问题等基本概念。

本章教学重点解释常微分方程解的几何意义。

（二）教学内容：1．由实际问题：质点运动即距离与时间关系（牛顿第二运动定律），放射性元素衰变过程，人口总数发展趋势估计等，通过建立数学模型，导出微分方程。

2．基本概念（常微分方程，偏微分方程，阶，线性，非线性，解，定解问题，特解，通解等）。

3．一阶微分方程组的几何定义，线素场（方向场），积分曲线。

4．常微分方程所讨论的基本问题。

第二章初等积分法（4，2）（一）本章教学目的与要求：要求学生熟练掌握分离变量法，常数变易法，初等变换法，积分因子法等初等解法。

本章教学重点对经典的几类方程介绍基本解法，勾通初等积分法与微积分学基本定理的关系。

并通过习题课进行初步解题训练，提高解题技巧。

（二）教学内容：１. 恰当方程（积分因子法）; ２. 分离变量法３. 一阶线性微分方程（常数变易法）４. 初等变换法（齐次方程，伯努利方程，黎卡提方程）5．应用举例第三章常微分方程基本定理（10，2）（一）本章教学目的与要求：要求学生正确掌握存在和唯一性定理及解的延伸的含义，熟记初值问题的解存在唯一性条件，正确理解解对初值和参数的连续依赖性和可微性的几何含意。

《常微分方程》课程教学大纲一、课程基本信息课程代码：110044课程名称：常微分方程英文名称：Ordinary Differential Equation课程类别：专业必修课学时：45学 分：2.5适用对象: 信息与计算科学本科考核方式：考试先修课程：数学分析、高等代数二、课程简介本课程是信息与计算科学专业的专业必修课程。

常微分方程（ODE）涉及经济学、管理学、生物学、工程技术等很多学科，是各学科紧密相连综合交叉的一门新学科。

This course is information and the professional professional required course of calculation science. Often the differential calculus square distance(ODE) involve economics, management to learn, biology, engineering technique's etc. is a lot of academicses, is each academics is close and conjoint comprehensive cross of a new academics.三、课程性质与教学目的通过本课程的理论学习和实践训练，提高学生的常微分方程水平，加深微积分训练，加强与其他数学课、物理、化学、生态学等方面的横向联系，能够全面正确地分析常微分方程在几何、物理、化学等学科应用过程中所出现的问题。

培养学生初步建模的能力，为后续课程的学习打下良好的基础，将来能综合运用所学知识解决问题。

四、教学内容及要求第一章初等积分法（一）目的与要求介绍常微分方程的相关概念，阐述其基本功能、相应的解法和应用等。

1．掌握常微分方程的基本概念；2．掌握可分离变量方程、齐次方程的概念及它们的联系和解法；3．掌握一阶线性微分方程、伯努利方程的概念及它们的联系和解法；4. 掌握全微分方程与积分因子的概念和解法；5. 掌握可降阶的二阶微分方程的解法；6. 掌握微分方程的应用方法，能建立一些简单的模型。

数学与应用数学专业教学大纲目录
1、数学分析
2、高等代数
3、解析几何
4、大学物理
5、复变函数
6、常微分方程
7、中学数学教学法
8、初等代数研究
9、几何画板
10、实变函数
11、计算方法
12、概率论与数理统计
13、数学模型与数学实验
14、Abstract algebra
15、泛函分析
16、微分几何
17、初等几何研究
18、数学分析选讲
19、高等代数选讲
20、线性统计模型
21、运筹学
22、随机过程
23、竞赛数学
24、数学教育评价
25、中学数学解题研究
26、初等数论
27、Introduction to graph theory
28、组合数学
29、点集拓扑
30、数学史
31、偏微分方程
32、数学方法论
33、精算概论
34、生物数学
35、现代密码学
36、分形
37、计量经济学
38、小波分析
39、模糊数学
40、时间序列分析。

教学大纲1、课程基础：本课程是数学学科的专业基础课，需要数学分析，线性代数和普通物理中的力学部分作为学习基础。

2、教材及主要参考书：教材：[1] 常微分方程，伍卓群、李勇，高等教育出版社, 2004。

主要参考书：[2] 常微分方程讲义，王柔怀、伍卓群，高等教育出版社，1963。

[3] 常微分方程讲义(第二版)，叶彦谦，人民教育出版社，1982。

[4] 常微分方程教程，丁同仁、李承治，高等教育出版社，1991。

3、教学内容和要点：第一章初等积分法一、学习目的要求掌握微分方程的相关概念；能熟练应用初等积分法求解典型类型方程；能灵活应用各种变换求方程的解；掌握一阶隐方程的解法。

二、主要教学内容1. 例子与概念2. 典型方程的解法3. 解题的灵活性4. 一阶隐方程，高阶方程与黎卡提方程第二章线性方程一、学习目的要求理解并掌握线性方程的一般理论，包括初值问题解的存在与唯一性、齐次和非齐次线性方程的通解的结构、边值问题解的存在性和马赛拉准则，掌握求解高阶线性微分方程的降阶法和复值解的概念。

二、主要教学内容1. 解的存在性与唯一性2. 齐次线性方程的通解的结构3. 非齐次线性方程的通解的结构4. 边值问题和周期解5. 线性微分方程的一些求解方法6. 线性方程的复值解第三章常系数线性方程一、学习目的要求掌握常系数齐次线性方程（组）的解法；能熟练应用算子解法求解非齐次线性方程；了解拉氏变换法；二、主要教学内容1. 常系数齐次线性方程的解法2. 常系数齐次线性方程组的解法3. 算子解法4. 拉氏变换法*第四章一般理论一、学习目的要求理解并掌握一般非线性微分方程的一般理论：包括初值问题的皮卡存在与唯一性定理、皮亚诺存在定理、柯西存在与唯一性定理、解的延展与解的整体存在性以及解对初值与参数的连续性与可微性，了解求解非线性方程的连续性方法。

二、主要教学内容1. 皮卡存在与唯一性定理2. 皮亚诺存在定理3. 柯西存在与唯一性定理*4. 解的延展与解的整体存在性5. 解对初值与参数的连续性6. 解对初值与参数的可微性7. 解非线性方程的连续性方法*第五章定性理论一、学习目的要求理解李雅普诺夫意义下解的稳定性定义，会运用第一近似方法和李雅普诺夫第二方法判别方程平衡解的稳定性；掌握一般定性理论的基本概念；掌握平面动力系统的奇点类型和闭轨附近的动力学行为；了解系统的结构稳定性，分支与浑沌等概念；掌握首次积分的定义和性质；了解守恒系统的基本性质。

常微分方程与偏微分方程常微分方程和偏微分方程是数学领域中的两个重要概念。

它们在物理学、工程学和经济学等领域中有着广泛的应用。

本文将探讨常微分方程和偏微分方程的定义、特点、求解方法以及在实际问题中的应用。

一、常微分方程常微分方程（Ordinary Differential Equation，简称ODE）是指只涉及一个自变量的微分方程。

一般形式如下：$F\left(x, y, \frac{{dy}}{{dx}},\frac{{d^2y}}{{dx^2}}, ...,\frac{{d^ny}}{{dx^n}}\right) = 0$其中，$y = y(x)$是未知函数，$F$是关于$x$和$y$及其导数的函数。

常微分方程按阶数可分为一阶、二阶等，按类型可分为线性、非线性等。

解常微分方程的方法有解析解和数值解。

解析解是通过代数和微积分方法求得的精确解。

数值解是通过近似计算和数值迭代方法求得的近似解。

常见的求解方法包括分离变量法、常数变易法、特解叠加法等。

常微分方程在物理学、电路理论、生物学等领域中有广泛的应用。

例如，牛顿第二定律可用常微分方程形式表示为$m\frac{{d^2x}}{{dt^2}} = F$，其中$m$为物体的质量，$\frac{{d^2x}}{{dt^2}}$是物体的加速度，$F$是物体受到的合力。

二、偏微分方程偏微分方程（Partial Differential Equation，简称PDE）是指涉及未知函数的偏导数的方程。

一般形式如下：$F\left(x, y, \frac{{\partial y}}{{\partial x}},\frac{{\partial^2y}}{{\partial x^2}},...,\frac{{\partial^ny}}{{\partial x^n}}, \frac{{\partial y}}{{\partial t}}, \frac{{\partial^2y}}{{\partialt^2}},...,\frac{{\partial^ny}}{{\partial t^n}}\right) = 0$其中，$y = y(x, t)$是未知函数，$F$是关于$x$、$t$和$y$及其偏导数的函数。

常微分方程与偏微分方程在数学领域中，微分方程是一类用导数或者微分来描述关系的方程。

微分方程主要分为常微分方程和偏微分方程两大类。

它们在科学和工程领域中具有广泛的应用，是研究自然界中变化和运动的重要工具。

本文将介绍常微分方程和偏微分方程的基本概念、求解方法以及应用领域。

一、常微分方程常微分方程是指未知函数只包含一个自变量的微分方程。

常微分方程的一般形式可以表示为：dy/dx = f(x, y)，其中y是未知函数，f(x, y)是已知的函数。

常微分方程可以分为一阶和高阶两类。

1. 一阶常微分方程一阶常微分方程是指未知函数y的导数只涉及到一阶导数的微分方程。

常见的一阶常微分方程有线性方程、分离变量方程和恰当方程等。

（这里可以具体介绍一下一阶常微分方程的概念和求解方法，可以包括分离变量法、线性方程求解和恰当方程求解等）2. 高阶常微分方程高阶常微分方程是指未知函数y的导数涉及到高阶导数的微分方程。

高阶常微分方程的求解方法通常是通过降阶和代换的方式转化为一阶常微分方程进行求解。

（这里可以具体介绍一下高阶常微分方程的概念和求解方法，可以包括代换法、降阶法和特征方程法等）二、偏微分方程偏微分方程是指未知函数包含多个自变量的微分方程。

偏微分方程的一般形式可以表示为：F(x, y, u, ∂u/∂x, ∂u/∂y, ∂²u/∂x², ∂²u/∂y², ...) = 0，其中u是未知函数，F是已知的函数。

偏微分方程的求解方法通常需要用到分离变量法、特征线法、变换法等。

（这里可以具体介绍一下偏微分方程的概念和求解方法，可以包括分离变量法、特征线法和变换法等）三、常微分方程与偏微分方程的应用常微分方程和偏微分方程在科学和工程领域中具有广泛的应用。

它们可以描述物理系统的运动、传热传质、波动方程、量子力学等现象。

具体应用包括以下几个方面：1. 物理学中的应用微分方程在描述物理系统的运动、振动和等稳定状态方面具有重要应用。