行星轮系及其传动比详解

第6章轮系本章主要介绍轮系的分类和应用，轮系传动比的计算方法。

由单对齿轮组成的齿轮机构功能单一，不能满足工程上的复杂要求，故常采用若干对齿轮，组成轮系来完成传动要求。

按轮系运动时轴线是否固定，将其分为两大类：（1）定轴轮系轮系运动时，所有齿轮轴线都固定的轮系，称为定轴轮系，如图1-1所示。

（2）行星轮系轮系运动时，至少有一个齿轮的轴线可以绕另一根齿轮的轴线转动，这样的轮系称为行星轮系。

轴线可动的齿轮称为行星轮，如图1-2中轮2，它既绕本身的轴线自转，又绕O1或O H公转。

轮1与轮3的轴线固定不动，称为太阳轮。

图1-1图1-21.1 定轴轮系定轴轮系分为两大类：一类是所有齿轮的轴线都相互平行，称为平行轴定轴轮系（亦称平面定轴轮系）；另一类轮系中有相交或交错的轴线，称之为非平行轴定轴轮系（亦称空间定轴轮系）。

轮系中，输入轴与输出轴的角速度或转速之比，称为轮系传动比。

计算传动比时，不仅要计算其数值大小，还要确定输入轴与输出轴的转向关系。

对于平行轴定轴轮系，其转向关系用正、负号表示：转向相同用正号，相反用负号。

对于非平行轴定轴轮系，各轮转动方向用箭头表示。

1.1.1 平行轴定轴轮系图1-1所示为各轴线平行的定轴轮系，输入轴与主动首轮1固联，输出轴与从动末轮5固联，所以该轮系传动比，就是输入轴与输出轴的转速比，其传动比i求法如下：（1）由图1-1所示轮系机构运动简图，可知齿轮动力传递线为：（1—2）＝（2′—3）＝（3′—4）＝（4—5）上式括号内是一对啮合齿轮，其中轮1、2′、3′、4为主动轮，2、3、4、5为从动轮；以 “—”所联两轮表示啮合，以“＝”所联两轮同轴运转，它们的转速相等。

（2） 传动比i 的大小()4543321245342312354433221511i i i i z z z z z z z zn n n n n n n n n n i ⋅⋅⋅=⋅⋅⋅-=⋅⋅⋅=='''''' 上式表明，该定轴齿轮系的传动比等于各对啮合齿轮传动比的连乘积，也等于各对啮合齿轮中各从动轮齿数的连乘积与各主动轮齿数的连乘积之比，其正负号取决于轮系中外啮合齿轮的对数。

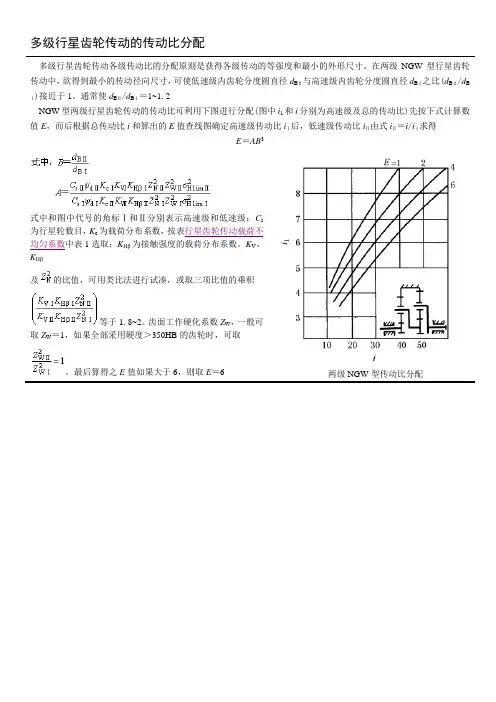
多级行星齿轮传动的传动比分配
多级行星齿轮传动各级传动比的分配原则是获得各级传动的等强度和最小的外形尺寸。

在两级NGW型行星齿轮传动中，欲得到最小的传动径向尺寸，可使低速级内齿轮分度圆直径d BⅡ与高速级内齿轮分度圆直径d BⅠ之比(d BⅡ/d B Ⅰ)接近于1。

通常使d BⅡ/d BⅠ＝1~1.2
NGW型两级行星齿轮传动的传动比可利用下图进行分配(图中i1和i分别为高速级及总的传动比)先按下式计算数值E，而后根据总传动比i和算出的E值查线图确定高速级传动比iⅠ后，低速级传动比iⅡ由式iⅡ＝i/iⅠ求得
E＝AB3
式中和图中代号的角标Ⅰ和Ⅱ分别表示高速级和低速级；C s
为行星轮数目，K c为载荷分布系数，按表行星齿轮传动载荷不
均匀系数中表1选取；K Hβ为接触强度的载荷分布系数。

K V、
K Hβ
及的比值，可用类比法进行试凑，或取三项比值的乘积
等于1.8~2。

齿面工作硬化系数Z W，一般可
取Z W＝1，如果全部采用硬度＞350HB的齿轮时，可取。

最后算得之E值如果大于6，则取E＝6 两级NGW型传动比分配。

大行星齿轮传动比计算公式大行星齿轮传动是一种常用的传动方式，广泛应用于工程机械、汽车等领域。

在设计和分析大行星齿轮传动系统时，计算传动比是非常重要的一步。

本文将介绍大行星齿轮传动比的计算公式及其应用。

一、大行星齿轮传动的基本结构大行星齿轮传动由太阳齿轮、行星齿轮、内齿圈和行星架等部分组成。

其中，太阳齿轮固定不动，内齿圈与外部传动轴相连，行星齿轮通过行星架与太阳齿轮和内齿圈相连。

二、大行星齿轮传动比的定义大行星齿轮传动比是指输入轴（太阳齿轮）的转速与输出轴（内齿圈）的转速之比。

传动比的大小决定了输出轴的转速和扭矩。

三、大行星齿轮传动比的计算公式大行星齿轮传动比可以根据行星齿轮传动的结构特点进行计算。

以下是常用的两种计算公式：1. 太阳齿轮传动比公式传动比=（内齿圈齿数+太阳齿数）/太阳齿数2. 行星齿轮传动比公式传动比=内齿圈齿数/行星齿数以上两种计算公式适用于不同的大行星齿轮传动结构，根据实际情况选择合适的公式进行计算。

四、大行星齿轮传动比的应用大行星齿轮传动比的计算在工程设计和分析中具有重要的意义。

以下是一些常见的应用场景：1. 机械设计中，通过计算传动比可以确定输出轴的转速和扭矩，从而满足设计要求。

2. 汽车传动系统中，大行星齿轮传动被广泛应用于变速器中。

通过计算传动比，可以实现不同档位之间的转速匹配，提高汽车的行驶性能和燃油经济性。

3. 工程机械中，大行星齿轮传动常用于液压马达的传动系统。

通过计算传动比，可以确定液压马达的输出速度和扭矩，从而实现机械装置的正常工作。

五、总结大行星齿轮传动比的计算是大行星齿轮传动系统设计和分析中的重要环节。

本文介绍了大行星齿轮传动比的计算公式及其应用，希望对读者理解和应用大行星齿轮传动有所帮助。

六、参考文献1. 《机械设计基础》（杨文彬、陈涛著，中国水利水电出版社）2. 《汽车传动系统设计与分析》（郑敏著，机械工业出版社）。

行星轮系传动行星轮系传动是一种常见的传动方式，广泛应用于各种机械设备中。

它由太阳轮、行星轮、内齿轮和外齿轮组成，通过它们之间的相互啮合来传递动力和扭矩。

行星轮系传动的工作原理是利用行星轮的旋转来传递动力。

太阳轮位于行星轮系的中心，通过输入轴将动力传递给太阳轮。

太阳轮的运动驱动行星轮绕太阳轮旋转，行星轮上还有一个轮系内齿轮，内齿轮与行星轮同心安装在行星架上。

内齿轮与外齿轮啮合，外齿轮固定不动。

当太阳轮传递动力时，行星轮会绕太阳轮旋转，并且行星轮上的内齿轮也会与外齿轮啮合。

这样，太阳轮的运动通过行星轮传递给内齿轮，再经过外齿轮传递给输出轴。

由于内齿轮与外齿轮的传动比不同，所以输出轴的转速和扭矩可以根据需要进行调节。

行星轮系传动具有多种优点。

首先，它具有高传动比和高扭矩输出的特点。

由于行星轮系中太阳轮和行星轮的啮合点分布在多个行星轮上，因此行星轮系传动可以实现比其他传动更高的传动比。

此外，行星轮系传动还可以通过增加行星轮的数量来提高扭矩输出。

行星轮系传动具有结构紧凑、体积小的特点。

行星轮系中的各个元件都可以紧凑地安装在一起，占用空间相对较小。

这使得行星轮系传动在有限空间内的应用更加方便。

行星轮系传动还具有平稳运转和传动效率高的优点。

由于行星轮系中的多个齿轮共同传递动力，使得传动过程相对平稳，减小了振动和噪音。

同时，由于行星轮系中的齿轮啮合面积大，传动效率相对较高。

然而，行星轮系传动也存在一些局限性。

首先，由于行星轮系中的多个齿轮的运动状态和相互作用比较复杂，因此制造和安装的难度相对较大。

其次，行星轮系传动的零件数量较多，加工和维修成本较高。

总的来说，行星轮系传动是一种广泛应用的传动方式，具有高传动比、高扭矩输出、结构紧凑、运转平稳和传动效率高的特点。

它在各种机械设备中发挥着重要作用，包括工业机械、汽车传动、航天器和机器人等领域。

随着科技的不断发展，行星轮系传动在设计和制造方面也得到了不断的改进和完善，为各行业的发展提供了可靠的动力传递解决方案。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此,只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 a cx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子:在此例中,要求出e ab i ＝?，如果行星架固定不动的话,这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出:e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了.定轴传动的传动比就好办了,直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100,z 2=101，z 2' =100 ,z 3=99.其输入件对输出件1的传动比i H1)1(111331311H H H H i i i i -===这样就把行星传动的计算转换为定轴传动了,所以将齿数代入公式得出1H i ＝10000最后愿我的这篇小文章能够给大家带来一点点帮助,我就心满意足了,在此感谢我读大学时的机械原理老师沈守范教授。

行星齿轮传动设计引言行星齿轮传动是一种常见的机械装置，广泛应用于工业、汽车、航空航天等领域。

其特点是结构紧凑、传动比大、承载能力强等优点。

本文将介绍行星齿轮传动的基本原理和设计步骤。

基本原理行星齿轮传动由太阳轮、行星轮和内齿轮组成。

太阳轮是固定不动的，行星轮绕太阳轮旋转，内齿轮与行星轮上的齿轮啮合。

传动比由太阳轮的齿数、行星轮的齿数和内齿轮的齿数共同决定。

行星齿轮传动的基本原理如下：1.太阳轮转动一周，行星轮转动n周；2.太阳轮齿数与行星轮齿数之比为1：n；3.太阳轮齿数与内齿轮齿数之比为1：(n+1)；根据上述原理，可以计算出行星齿轮传动的传动比和输入输出的转速关系。

设计步骤进行行星齿轮传动的设计，需要按照以下步骤进行：1.确定输入和输出参数：包括输入功率、输入转速、输出转速、传动比等；2.选择行星轮和太阳轮的齿数：根据传动比和输入输出转速关系，选择合适的行星轮和太阳轮的齿数；3.确定行星轮的位置：行星轮通常有几颗，需要确定每颗行星轮的位置，以及行星轮与太阳轮的啮合方式；4.计算内齿轮的齿数：根据太阳轮和行星轮的齿数，计算出内齿轮的齿数；5.绘制行星齿轮传动的示意图：根据上述计算结果，绘制行星齿轮传动的示意图；6.进行传动效率计算：根据输入功率和输出功率，计算传动效率；7.进行强度计算：根据输入功率、传动比和材料强度等参数，计算行星齿轮传动的承载能力。

实例演示为了更好地理解行星齿轮传动的设计过程，以下是一个实例演示：假设输入功率为100W，输入转速为1000rpm，输出转速为500rpm，要求传动比为2：1。

1.根据输出转速和传动比，可以计算得到太阳轮的转速为250rpm；2.假设行星轮的齿数为30，太阳轮的齿数为60，可以得到行星轮的转速为500rpm；3.根据太阳轮和行星轮的齿数，可以计算出内齿轮的齿数为20；4.根据齿数的要求，确定行星轮位置为太阳轮外侧，并与太阳轮以外啮合城sk1；5.绘制行星齿轮传动的示意图如下：行星齿轮传动示意图行星齿轮传动示意图6.计算传动效率：根据输入功率和输出功率，可以计算传动效率为80%；7.强度计算：根据输入功率、传动比和材料强度等参数，可以计算行星齿轮传动的承载能力为xxx。

行星齿轮传动比8个公式
1.齿轮比计算公式：
齿轮比=-(R+2)/(R+1)，其中R为行星轮的齿数。

2.行星轮直径公式：
行星轮的直径可以通过行星轮齿数来计算。

行星轮直径=齿数*模数。

3.太阳轮直径公式：
太阳轮的直径可以通过太阳轮齿数来计算。

太阳轮直径=齿数*模数。

4.行星轮轮齿厚度公式：
行星轮的轮齿厚度可以通过行星轮直径和模数来计算。

行星轮轮齿厚度=2*模数。

5.太阳轮轮齿厚度公式：
太阳轮的轮齿厚度可以通过太阳轮直径和模数来计算。

太阳轮轮齿厚度=2*模数。

6.行星齿轮传动的速度比公式：
速度比=齿数A/齿数B，其中齿数A为太阳轮齿数，齿数B为行星轮齿数。

7.行星齿轮传动的扭矩比公式：
扭矩比=(半径A/半径B)^2，其中半径A为太阳轮半径，半径B为行星轮半径。

8.行星齿轮传动的传动效率公式：
传动效率=输出功率/输入功率。

综上所述，行星齿轮传动的8个常用公式分别是齿轮比计算公式、行星轮直径公式、太阳轮直径公式、行星轮轮齿厚度公式、太阳轮轮齿厚度公式、行星齿轮传动的速度比公式、行星齿轮传动的扭矩比公式和行星齿轮传动的传动效率公式。

这些公式帮助工程师在设计和计算行星齿轮传动时能够准确地确定齿轮比、轮齿尺寸和传动性能等参数，从而提高传动系统的可靠性和效率。

行星齿轮机构传动比计算方法Key words: epicyclic gear train; speed ratio; compute way.随着行星齿轮减速器以及行星齿轮传动在变速箱中的广泛应用，对行星齿轮传动的了解和掌握已成为工程技术人员的必要技能。

但是，对于刚接触行星齿轮传动的工程技术人员来说，行星齿轮传动的速比计算比较不容易理解和掌握。

本文通过对各类参考资料及教科书中的行星齿轮传动速比计算方法进行总结归纳，并针对常用的最具代表性的2K-H型行星齿轮传动，分别用不同方法对其传动特性方程进行了推导论证。

行星齿轮传动或称周转轮系。

根据《机械原理》[1]上的定义，我们可把周转轮系分为差动轮系和行星轮系。

为理解方便，本论文所讨论限于2K-H型周转轮系。

关于行星齿轮传动（周转轮系）的速比计算方法，归纳起来有两大类四种方法，分别为由行星架固定法和力矩法组成的分析法；由速度图解法和矢量法组成的图解法[2]。

矢量图解法一般适用于圆锥齿轮组成的行星齿轮传动，在此不作介绍；下面分别运用其它三种计算方法对2K-H型周转轮系的传动特性方程（1）进行推导。

1－太阳轮 2－行星轮 3－内齿圈 H －行星架 图1 行星齿轮传动Fig 1 Epicyclic gear train0)1(31=++-αωωαωH （1） 结合图1，式中1ω为太阳轮1的转速、Hω为行星架H 转速、3ω为内齿圈3转速、α为内齿圈3与太阳轮1的齿数比即13Z Z =α。

1 行星架固定法机械专业教科书上一般介绍的都是此种方法，也可叫转化机构法。

其理论是一位名叫Wlies 的科学家于1841年提出的，即“一个机构整体的绝对运动并不影响其内部各构件间的相对运动” [3]，就像手表的时针、分针、秒针的相对运动不会因带表人的行动而变化。

如图2所示，其中太阳轮1、行星轮2、内齿圈3、行星架H 的转速分别为Hωωωω、、、321。

我们假定整个行星轮系放在一个绕支点O 旋转的圆盘上，此圆盘的转速为 H ω-。

行星齿轮效率行星齿轮是一种常见的传动装置，具有高效率的特点。

在机械传动中，行星齿轮凭借其独特的结构和工作原理，成为提高传动效率的重要手段之一。

行星齿轮由太阳轮、行星轮和内齿圈组成，其中太阳轮为固定轮，行星轮和内齿圈可以绕着太阳轮旋转。

行星轮的齿数较少，与内齿圈的齿数相等，而太阳轮的齿数较多。

当太阳轮和内齿圈固定时，行星轮绕太阳轮旋转，实现传递动力。

行星轮与太阳轮和内齿圈之间的传动比关系为：传动比 = （太阳轮齿数 + 内齿圈齿数）/ 太阳轮齿数行星齿轮的高效率可以从以下几个方面解释：1. 大传动比：行星齿轮的传动比通常较大，这意味着输入的转速相对较小，可以减少机械损失，提高传动效率。

而且，行星齿轮传动比的变化范围较广，可以满足不同的传动需求。

2. 分摊负荷：行星齿轮传动中，负载会分摊到多个行星轮上，降低了单个齿轮的承载压力，减少了齿面磨损和齿面接触疲劳，提高了传动效率。

3. 平稳传动：行星齿轮传动过程中，行星轮的运动是平稳的，减少了振动和冲击，降低了传动损失，提高了传动效率。

4. 多级传动：行星齿轮传动可以通过增加行星轮和内齿圈的数量，实现多级传动，进一步提高传动效率。

多级传动可以平衡各级齿轮的负荷，减少传动中的能量损失。

5. 减少摩擦损失：行星齿轮传动中，齿轮之间的啮合是滚动摩擦，相比于其他传动方式的滑动摩擦，行星齿轮的摩擦损失较小，提高了传动效率。

6. 超前润滑：行星齿轮传动中，齿轮的润滑通常采用超前润滑方式，即在齿轮啮合前进行润滑，形成润滑膜，减少摩擦和磨损，提高传动效率。

行星齿轮作为一种高效率的传动装置，在机械工程中得到广泛应用。

其独特的结构和工作原理使其具有高传动比、分摊负荷、平稳传动、多级传动、减少摩擦损失和超前润滑等优点，能够有效提高传动效率。

在实际应用中，我们可以根据传动需求选择合适的行星齿轮传动方案，并合理设计传动参数，以实现高效率的传动效果。

行星轮系传动比计算（6-5b）例7.1-6汽车后桥差速器原理及实物模型如图a/b 所示. 已知各轮齿数及桥壳框架齿轮1的转速ω1(ω1由传动轴转速决定),求齿轮2、4(即汽车左、右两侧后轮)转速。

依题意知:z 2=z 4,z 3=z 5,假设各轮角速度方向如图c 所示,则有：对啮合点：对啮合点：对啮合点：对啮合点F D C A ⎪⎪⎭⎪⎪⎬⎫=+==-==+==-=255122455144433144233122r r r r r r r r r r r r r r r r r r r r GE GE GE GE GB GB GB GB ，，，，ωωωωωωωωωωωω⎪⎪⎩⎪⎪⎨⎧+=-=+=-=⇒551222551444331444331222ωωωωωωωωωωωωz z z z z z z z z z z z ⎪⎪⎨⎧+=-=331444331222ωωωωωωz z z z z z ⎪⎪⎨⎧+=-=⇒4331423312//ωωωωωωz z z z 解1用平面运动理论求解设各轮角速度方向如图c 所示,动系固连在轮1上.轮3绝对角速度：a =+ωωω31e =ωω1r = ωω3在动系中对啮合点A ：z2(ω2–ω1)=-z3ω3（1）在动系中对啮合点C ：z3ω3=z4(ω4–ω1)（2）在动系中对啮合点D ：z4(ω4–ω1)=-z5ω5（3）在动系中对啮合点F ：z5ω5=z2(ω2–ω1)（4）行星轮系传动比计算（6-5b ）解2用相对运动理论求解有缘学习更多＋谓ｙｇｄ３０７６考证资料或关注桃报：奉献教育（店铺）⎪⎩⎪⎨⎧-=+=-=⇒354331423312//ωωωωωωωωz z z z ω2 +ω4=2ω11、汽车直线行驶时左右两后轮转速相等(ω2 =ω4),⇒ω3 =ω5=0,ω2 =ω4=ω1。

2、汽车拐弯时左右两侧后轮转速不相等(ω2 ≠ω4 ) ⇒ω5= -ω3≠0。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+cba abc i i ――――――――――――――――――――――――1acxabx abc i i i =―――――――――――――――――――――――――2acbabc i i 1=――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如：在此例中，要求出eab i ＝？，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式acxabx abc i i i =将x 加进去，所以可以得出：ebxeaxeab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba a bc i i 了，所以)1()1(xbe xae ebxeaxeab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01ce bdae ce bdc e a c xbe xae ebxeaxeab ZZ Z ZZZ ZZ Z ZZ Z ZZ i i i i i ⨯-+=⨯--⨯--=--==再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。

行星齿轮传动比计算在《机械原理》上，行星齿轮求解是通过列一系列方程式求解，其求解过程繁琐容易出错，其实用不着如此，只要理解了传动比eab i 的含义，就可以很快地直接写出行星齿轮的传动比，其关键是掌握几个根据e ab i 的含义推导出来公式，随便多复杂的行星齿轮传动机构，根据这几个公式都能从头写到尾直接把其传动比写出来，而不要象《机械原理》里面所讲的方法列出一大堆方程式来求解。

一式求解行星齿轮传动比有三个基本的公式1=+c ba a bc i i ――――――――――――――――――――――――1 acx a bx abci i i = ―――――――――――――――――――――――――2 a cb abc i i 1= ――――――――――――――――――――――――――3熟练掌握了这三个公式后，不管什么形式的行星齿轮传动机构用这些公式代进去后就能直接将传动比写出来了。

关键是要善于选择中间的一些部件作为参照，使其最后形成都是定轴传动，所以这些参照基本都是一些行星架等例如象论坛中“大模王”兄弟所举的例子：在此例中，要求出e ab i ＝？，如果行星架固定不动的话，这道题目就简单多了，就是一定轴传动。

所以我们要想办法把e ab i 变成一定轴传动，所以可以根据公式a cx a bx a bci i i =将x 加进去， 所以可以得出：e bx e ax eab i i i =要想变成定轴传动，就要把x 放到上面去，所以这里就要运用第一个公式1=+c ba abc i i 了，所以)1()1(xbe x ae ebx e ax eab i i i i i --==所以现在eab i 就变成了两个定轴传动之间的关系式了。

定轴传动的传动比就好办了，直接写出来就可以了。

即)1()1())1(1())1(1()1()1(01c e bd ae c e b d c e a c x be x ae e bx e ax e ab Z Z Z Z Z Z Z Z Z Z Z Z Z Z i i i i i ⨯-+=⨯--⨯--=--== 再例如下面的传动机构：已知其各轮的齿数为z 1=100，z 2=101，z 2’ =100 ，z 3=99。