定轴轮系传动比的计算

定轴轮系传动比计算定轴轮系是一种常见的传动装置，由多个齿轮组成，用于传递转矩和转速。

传动比是定轴轮系的一个重要参数，它表示驱动齿轮转动一周时从动齿轮转动的圈数。

本文将介绍定轴轮系传动比的计算方法。

一、基本数据法基本数据法适用于简单的定轴轮系，即只有两个齿轮的情况。

在这种情况下，传动比等于从动齿轮的齿数除以驱动齿轮的齿数。

传动比=齿数比=齿数从/齿数驱其中，传动比大于1表示从动齿轮的转速大于驱动齿轮的转速，可以实现减速；传动比小于1表示从动齿轮的转速小于驱动齿轮的转速，可以实现增速；传动比等于1表示从动齿轮的转速和驱动齿轮的转速相等，实现传递。

例如，如果从动齿轮的齿数为20，驱动齿轮的齿数为40，则传动比为20/40=0.5，表示从动齿轮的转速是驱动齿轮的一半。

二、级联数据法级联数据法适用于复杂的定轴轮系，即多个齿轮组成的情况。

在这种情况下，可以根据级联原则逐个计算齿轮的传动比，然后将它们相乘得到总传动比。

级联原则是指当多个齿轮串联在一起时，相邻两个齿轮之间的传动比是相等的。

因此，只需要计算每个齿轮的传动比，再将它们相乘，即可得到总传动比。

例如，有一个定轴轮系由三个齿轮组成，齿数分别为A=10，B=20，C=30，其中A驱动B，B驱动C。

则传动比=A/B*B/C=10/20*20/30=1/3，表示从动齿轮的转速是驱动齿轮的1/3需要注意的是，在级联数据法中，传动比还受到齿轮的排列顺序的影响。

同样的齿轮，不同的排列顺序会导致不同的传动比。

因此，在实际应用中，必须根据具体的传动需求选择适当的齿轮排列顺序。

在计算定轴轮系的传动比时，还需要考虑其他一些因素。

例如，齿轮的啮合角和啮合系数会影响齿轮的传动效率和噪声。

齿轮的材料和制造精度也会影响齿轮的耐久性和工作平稳性。

因此，在实际设计中，必须综合考虑这些因素，选择适当的齿轮参数和传动比，在满足传动需求的同时兼顾传动效率和使用寿命。

总结起来，定轴轮系传动比的计算方法有基本数据法和级联数据法。

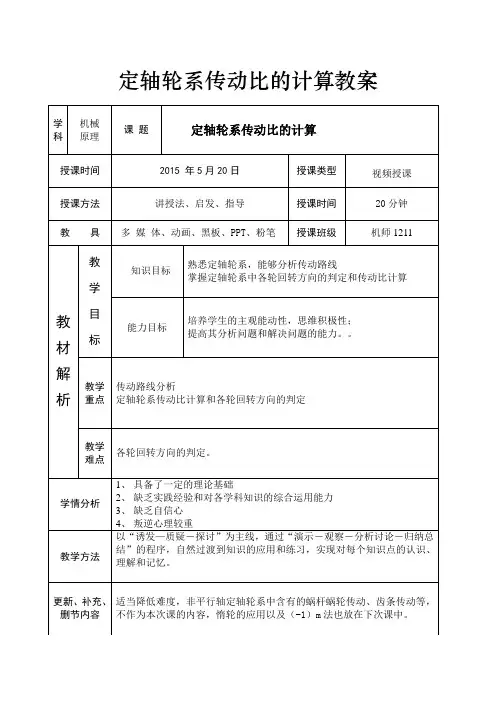
定轴轮系传动比的计算教案幻灯片20幻灯片17幻灯片18 例题：如图所示的轮系中，已知各轮齿数，齿轮1为主动轮203020221===ZZZ，，, r/min 计算齿轮1、6之间的传动比。

计算过程：大小清楚了之后，我们来讨论第二个问题任务2：定轴轮系中各轮转向的判断。

知识分解：无论多复杂的轮系，都是由若干个一对齿轮传动组成一对齿轮传动，当首轮（或末轮）的转向为已知时，其末轮（或首轮）的转向也就确定了，表示方法可以用标注箭头的方法来确定。

外啮合：两箭头指向相反。

内啮合：两箭头指向相同。

分析引导讲解示范分析引导讲解示范积极思考回答问题完成学案积极思考回答问题完成学案960,36304030602016'55'44'2=======nZZZZZZ，，，，积所有主动轮齿数的连乘积所有从动轮齿数的连乘===k1k11k nniωω2.73030202036406030542165426116=⨯⨯⨯⨯⨯⨯===∴'''zzzzzzzznni板书设计。

机械设计第10章机械传动系统及其传动比机械传动系统及其传动比案例导入：在实际的机械工程中，为了满足各种不同的工作需要，仅仅使用一对齿轮是不够的。

本章通过带式输送机、牛头刨床、汽车变速箱和差速器、自动进刀读数装置、滚齿机行星轮系等例子，介绍轮系的概念、分类、传动比的分析计算方法。

第一节定轴轮系的传动比计算在实际应用的机械中，为了满足各种需要，例如需要较大的传动比或作远距离传动等，常采用一系列互相啮合的齿轮来组成传动装置。

这种由一系列齿轮组成的传动装置称为齿轮系统，简称轮系。

一、轮系的分类轮系有两种基本类型：(1)定轴轮系。

如图10-1所示，在轮系运转时各齿轮几何轴线都是固定不变的，这种轮系称为定轴轮系。

(2)行星轮系。

如图10-2所示，在轮系运转时至少有一个齿轮的几何轴线绕另一几何轴线转动，这种轮系称为行星轮系。

图10-1 定轴轮系二、轮系的传动比1.轮系的传动比轮系中，输入轴（轮）与输出轴（轮）的转速或角速度之比，称为轮系的传动比，通常用i表示。

因为角速度或转速是矢量，所以，计算轮系传动比时，不仅要计算它的大小，而且还要确定输出轴（轮）的转动方向。

2.定轴轮系传动比的计算根据轮系传动比的定义，一对圆柱齿轮的传动比为nzi12 1 2 n2z1式中：“±”为输出轮的转动方向符号，图10-2行星轮系第十章机械传动系统及其传动比当输入轮和输出轮的转动方向相同时取“＋”号、相反时取“－”号。

如图10-1a) 所示的一对外啮合直齿圆柱齿轮传动，两齿轮旋转方向相反，其传动比规定为负值，表示为：i=n1=n2z2 z1如图10-1b)所示为一对内啮合直齿圆柱齿轮传动，两齿轮的旋转方向相同，其传动比规定为正值，表示为：n1z2 i= =n2z1如图10-3所示的定轴轮系，齿轮1为输入轮，齿轮4为输出轮。

应该注意到齿轮2和2＇是固定在同一根轴上的，即有n2=n2′。

此轮系的传图10-3定轴轮系传动比的计算动比i14可写为：nnn ni14 1 123 i12i2 3i***** z2z3z4 312上式表明，定轴轮系的总传动比等于各对啮合齿轮传动比的连乘积，其大小等于各对啮合齿轮中所有从动轮齿数的连乘积与所有主动轮齿数的连乘积之比，即m从1轮到k轮之间所有从动轮齿数n的连乘积i1k 1 1 (10-1) nk从1轮到k轮之间所有从主轮齿数的连乘积式中：m为平行轴外啮合圆柱齿轮的对数，用于确定全部由圆柱齿轮组成的定轴轮系中输出轮的转向。

老师出示小黑板给出每种齿轮副的端面图、侧面图要求学生在黑板上的端面图和侧面图上分别标出两轮转向，并写出其传动比公式。

二、新引入新课：教师接着展示定轴轮系模型，引导学生参与到演示教学中来，通过一对齿轮的传动比概念，教师提出问题：多个齿轮的传动比是否就是输入轴的转速与输出轴的转速之比？引发学生思考。

演示模型启发提问2分钟授新：一定轴轮系传动比公式推导和传动比定义的理解35分钟课讲授由以上两个齿轮传动的思路和以下例题的推导过程来推出定轴轮系传动比公式和定义分析步骤：1）分析该轮系的传动路线。

2）该轮系有几对齿轮组成？3）每一对啮合的齿轮中哪一个是主动轮？哪一个是从动轮？分别写出它们传动比公式。

4）在该轮系中分别有哪些齿轮是同轴的？注意：所有齿轮副传动比的连乘积就是该轮系的传动比。

514'3'21543354433221453423122)1(ωωωωωωωωωω=-==⋅⋅⋅⋅⋅⋅zzzzzzzziiii由以上定轴轮系的传动比公式得出其定义：定轴轮系传动比是指轮系中首末两轮的角速度(或转速)之比。

推广：设首轮A的转速为nA，末轮K的转速为nK，m为圆柱齿轮外啮合的对数，则平面定轴轮系的传动比可写为：◆其中：m为外啮合圆柱齿轮副的数目◆结果为正：两轮回转方向相同◆结果为负：两轮回转方向相反◆思考：齿轮4在图中位置有什么特殊地方？在公式中有什么特点？对轮系的传动比有何影响？齿轮4既是齿轮3´的从动轮又是齿轮5的主动轮；它的齿数或转数在公式中既作分子又作分母；只改变齿轮副中从动轮教师引导学生通过从模型到简图按着这几个步骤一步步分析来掌握对轮系的读图，通过推导得出定期轴轮系传动比公式。

要求学生理解、领会定轴轮系传动比公式。

122’3 3’45122112zzi-==ωω'233223zzi==ωω'344334zzi-==ωω455445zzi-==ωω回转方向而不影响齿轮副传动比的大小——惰轮（过桥轮）惰轮作用：1、实现换向1）2）◆总结:外啮合时加偶数惰轮时，齿轮副的主、从动轮的回转方向是相反的◆外啮合时加奇数惰轮时，齿轮副的主、从动轮的回转方向是相同的2、延长传动距离，所以又称过桥轮。

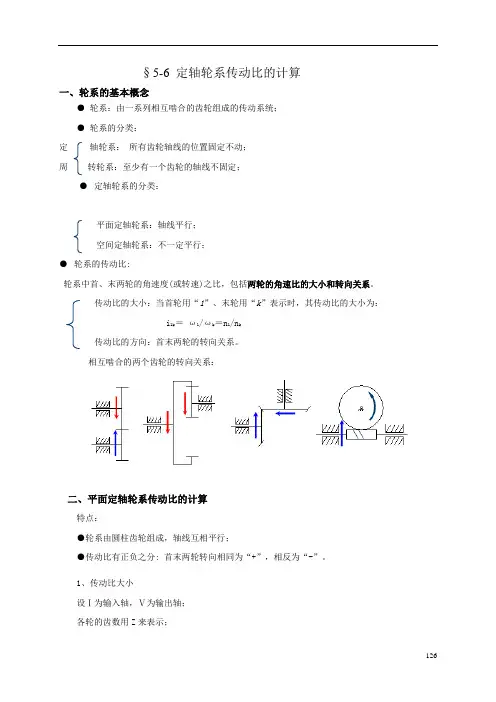
§5-6 定轴轮系传动比的计算一、轮系的基本概念●轮系：由一系列相互啮合的齿轮组成的传动系统；●轮系的分类：定轴轮系：所有齿轮轴线的位置固定不动；周转轮系：至少有一个齿轮的轴线不固定；●定轴轮系的分类：平面定轴轮系：轴线平行；空间定轴轮系：不一定平行；●轮系的传动比:轮系中首、末两轮的角速度(或转速)之比，包括两轮的角速比的大小和转向关系。

传动比的大小：当首轮用“1”、末轮用“k”表示时，其传动比的大小为：i1k＝ω1/ωk＝n1/n k传动比的方向：首末两轮的转向关系。

相互啮合的两个齿轮的转向关系：二、平面定轴轮系传动比的计算特点：●轮系由圆柱齿轮组成，轴线互相平行；●传动比有正负之分: 首末两轮转向相同为“+”，相反为“-”。

1、传动比大小设Ⅰ为输入轴，Ⅴ为输出轴；各轮的齿数用Z来表示；126127角速度用ω表示；首先计算各对齿轮的传动比：所以：结论： 定轴轮系的传动比等于各对齿轮传动比的连乘积，其值等于各对齿轮的从动轮齿数的乘积与主动轮齿数的乘积之比； 2、传动比方向在计算传动比时，应计入传动比的符号： 首末两轮转向相同为“+”，相反为“-”。

（1）公式法式中：m 为外啮合圆柱齿轮的对数 举例：（2）箭头标注法采用直接在图中标注箭头的方法来确定首末两轮的转向，转向相同为“+”，相反为“-”。

举例：122112z z i ==ωω32223332z i z ωωωω'''===33434443z i z ωωωω'''===455445z z i ==ωω11211)1(--==k km k k z z z z i K K ωω三、空间定轴轮系的传动比特点：●轮系中包含有空间齿轮（如锥齿轮、蜗轮蜗杆、螺旋齿轮等）；●首末两轮的轴线不一定平行。

1 传动比的大小2 传动比的方向注意：只能采用箭头标注法，不能采用(-1)m法判断。

分两种情况讨论：情况1：首、末两轮轴线平行传动比计算式前应加“+”、“-”号，表示两轮的转向关系。

行星轮系传动比的计算
回忆上节内容:定轴轮系传动比的计算公式为:i1k=n1/nk=i1*i2*i3* (i)
定轴轮系的特点是:每个齿轮都是围绕固定的周线旋转,没有自身的公转.
今天我们看以下行星轮系,请同学们思考:行星的运动特点?
对,行星一方面不仅围绕固定的轴线旋转,而且会围绕太阳公转.
下面这张图就是行星轮系,结构和特点我们看一下:
结构:齿圈,太阳轮,行星轮,行星齿轮架
原理:行星齿轮不仅自转,还有围绕太阳轮的公转.
计算传动比:转化法:化行星轮系为定轴轮系
简化结构如下:
太阳轮:n1 z1
行星轮:n2 z2
齿圈:n3 z3
行星架:nh Zh
则传动比计算公式为:ng-nh/nk-nh=(-1)m齿轮G,K之间所有从动轮齿数的连乘积/齿轮G,K之间所有主动轮齿数的连乘积
例题:如图所示为圆锥齿轮组成的差动轮系,Z1=Z2=Z3,求齿轮1,3和行星架H三者转速的关系
解:该轮系为差动轮系,其中齿轮1,3及行星架H的轴线均互相平行或重合,将齿轮1看作主动轮,齿轮3看作从动轮,并设齿轮1的转向为正,通过画箭头,齿轮3的箭头与齿轮1 的相反,故为负,由公式计算:
N1-nh/n3-nh=-z2z3/z1z2=-z3/z1=-1
所以三者转速关系为:
2nh=n1+n3
分析:行星轮系在汽车上的应用:1.汽车后桥差速器。