基于comsol的悬臂梁形变实验报告

悬臂梁冲击实验报告悬臂梁冲击实验报告引言：悬臂梁是一种常见的结构，在工程设计中经常使用。

为了了解悬臂梁在冲击力下的性能表现，我们进行了一系列的实验。

实验目的：本实验的目的是通过对悬臂梁进行冲击实验，研究悬臂梁在冲击力作用下的变形和破坏情况，并分析其受力特点和结构性能。

实验装置：实验装置主要包括悬臂梁、冲击装置和数据采集系统。

悬臂梁选用了一根长度为1米、截面为矩形的钢材，冲击装置采用了一块重锤和一个万能试验机作为冲击源，数据采集系统用于记录悬臂梁在冲击过程中的位移和应力变化。

实验步骤：1. 将悬臂梁固定在实验台上，并调整好冲击装置的位置。

2. 在悬臂梁上设置合适的测点，用于记录位移和应力变化。

3. 开始进行冲击实验，将重锤从一定高度自由落下，冲击到悬臂梁上。

4. 实时记录悬臂梁的位移和应力变化，并保存数据供后续分析。

实验结果：通过实验记录的数据，我们得到了悬臂梁在冲击过程中的位移和应力变化曲线。

从曲线中可以看出，悬臂梁在受到冲击力后发生了明显的挠曲变形，同时也出现了应力集中的情况。

随着冲击力的增大，悬臂梁的挠曲程度和应力集中程度也逐渐增加。

讨论与分析：根据实验结果，我们可以得出以下结论：1. 冲击力对悬臂梁的挠曲变形和应力集中有着明显的影响。

冲击力越大，悬臂梁的变形和应力集中程度越明显。

2. 悬臂梁的结构特点使其在冲击力作用下容易发生挠曲变形。

这是由于悬臂梁只有一个支点，无法均匀分布冲击力。

3. 在实际工程设计中，需要考虑悬臂梁在冲击力下的性能表现，采取合适的措施来增强悬臂梁的抗冲击能力。

结论：通过本次实验，我们对悬臂梁在冲击力下的性能表现有了更深入的了解。

悬臂梁在受到冲击力时会发生明显的挠曲变形和应力集中，这对工程设计和结构安全具有重要意义。

在实际应用中，需要根据具体情况采取相应的措施来增强悬臂梁的抗冲击能力，确保结构的安全可靠性。

总结：本实验通过对悬臂梁的冲击实验，研究了悬臂梁在冲击力下的变形和破坏情况，并分析了其受力特点和结构性能。

实验 等截面悬臂梁模态测试实验一、 实验目的1. 熟悉模态分析原理；2. 掌握悬臂梁的测试过程。

二、 实验原理1. 模态分析基本原理理论上，连续弹性体梁有无限多个自由度，因此需要无限多个连续模型才能描述，但是在实际操作中可以将连续弹性体梁分为n 个集中质量来研究。

简化之后的模型中有n 个集中质量，一般就有n 个自由度，系统的运动方程是n 个二阶互相耦合（联立）的常微分方程。

这就是说梁可以用一种“模态模型”来描述其动态响应。

模态分析的实质，是一种坐标转换。

其目的在于把原在物理坐标系统中描述的响应向量，放到所谓“模态坐标系统”中来描述。

这一坐标系统的每一个基向量恰是振动系统的一个特征向量。

也就是说在这个坐标下，振动方程是一组互无耦合的方程，分别描述振动系统的各阶振动形式，每个坐标均可单独求解，得到系统的某阶结构参数。

多次锤击各点，通过仪器记录传感器与力锤的信号，计算得到第ｉ个激励点与定响应点（例如点2）之间的传递函数H i (ω)，从而得到频率响应函数矩阵中的一行频响函数的任一行包含所有模态参数，而该行的r 阶模态的频响函数 的比值，即为r 阶模态的振型。

2. 激励方法为进行模态分析，首先要测得激振力及相应的响应信号，进行传递函数分析。

传递函数分析实质上就是机械导纳，i 和j 两点之间的传递函数表示在[]∑==Nr iN ri ri r H H H 121...[]Nr r r Nr rr r irk c j m ϕϕϕωωϕ (2112)∑=++-=[]{}[]Tr ir Nr r iN i i Y H H H ϕϕ∑==121...j点作用单位力时，在i点所引起的响应。

要得到i和j点之间的传递导纳，只要在j点加一个频率为ω的正弦的力信号激振，而在i点测量其引起的响应，就可得到计算传递函数曲线上的一个点。

如果ω是连续变化的，分别测得其相应的响应，就可以得到传递函数曲线。

根据模态分析的原理，我们要测得传递函数矩阵中的任一行或任一列，由此可采用不同的测试方法。

实验四悬臂梁动应变的测定
一：实验目的
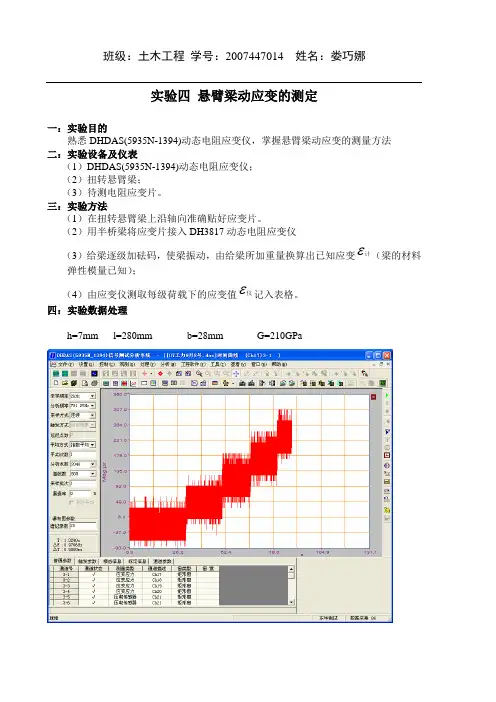
熟悉DHDAS(5935N-1394)动态电阻应变仪，掌握悬臂梁动应变的测量方法
二：实验设备及仪表
（1）DHDAS(5935N-1394)动态电阻应变仪；
（2）扭转悬臂梁；
（3）待测电阻应变片。

三：实验方法
（1）在扭转悬臂梁上沿轴向准确贴好应变片。

（2）用半桥梁将应变片接入DH3817动态电阻应变仪
ε计（梁的材料（3）给梁逐级加砝码，使梁振动，由给梁所加重量换算出已知应变
弹性模量已知）；
ε仪记入表格。

（4）由应变仪测取每级荷载下的应变值
四：实验数据处理
h=7mm l=280mm b=28mm G=210GPa
五：结论
通过该实验掌握了DHDAS(5935N-1394)动态电阻应变仪的使用方法，熟悉了实验
过程，为下面实验的动态分析打下了良好的实验基础。

悬臂梁弯扭组合变形设计案例咱们来聊一个悬臂梁弯扭组合变形的设计案例，就像搭积木一样，但这个积木可是有大学问的。

想象一下，有一个机械手臂，它就像是一个悬臂梁。

这个机械手臂在工作的时候啊，可不光是受到一种力的作用，而是弯扭组合的变形情况。

一、项目背景。

这个机械手臂呢，要在一个自动化生产线上工作。

它需要伸出去抓取零件，然后再把零件放到指定的位置。

在这个过程中，手臂一端固定在机器上（这就是悬臂梁的固定端啦），另一端自由活动。

由于抓取的零件重量不一样，而且手臂运动的速度和方向也会变化，所以就产生了弯曲和扭转这两种变形情况。

二、受力分析。

1. 弯曲力。

当手臂伸出去抓取零件的时候，零件的重量就像一个小坏蛋，使劲儿地把手臂往下拽，这就产生了弯曲力。

比如说，我们抓取一个5千克的零件，假设手臂长度是1米，这个零件的重力就会在手臂上产生一个弯矩。

根据弯矩的计算公式M = FL（这里F就是零件的重力，L就是手臂的长度），那这个弯矩就是M = 5×9.8×1 = 49牛·米（这里g = 9.8米/秒²）。

这个弯矩就会让手臂像被掰弯的小树枝一样，有弯曲变形的趋势。

2. 扭转力。

然后呢，当手臂转动把零件送到指定位置的时候，这个转动就产生了扭转力。

比如说，手臂要以一定的角速度转动，就像拧麻花一样，在手臂的轴线上就会产生扭矩。

假设手臂的转动惯量是I，角加速度是α，根据扭矩的计算公式T=Iα。

如果手臂快速地转动，这个扭矩可就不小了，它会让手臂产生扭转变形。

三、材料选择。

考虑到这种弯扭组合变形的情况，我们得找个厉害的材料来做这个悬臂梁（也就是机械手臂）。

经过一番挑选，我们选择了高强度合金钢。

为啥呢？这种材料就像钢铁侠的盔甲一样，又硬又结实。

它的屈服强度高，能够承受较大的弯曲和扭转应力。

比如说，它的屈服强度可以达到800兆帕，这就意味着在这么大的压力下，材料才会开始变形得很厉害。

而且它的韧性也不错，不会轻易断裂，就像一个坚强又有弹性的战士，能够在复杂的受力情况下保持稳定。

实验报告悬臂梁的模态实验姓名： xxx学号： xxx专业： xxx系别： xxx一、试验装置二、实验原理本实验采用锤击法测定悬臂梁的频响函数，将第S 点沿坐标X S 方向作用的锤击力和第r 点沿X r 方向的响应分别由相应的传感器转换为电信号，在由动态分析仪，按照随机振动理论，运算得出r,s 两点间的频响函数rs H ~，∑=+-==ni i i i k i s i r s r rs i k F X H 12)()()(0)21(~~λζλϕϕ （1） 又由于响应信号是加速度，同时圆频率为ω，位移函数,sin t X x ω=其加速度为,sin 22x t X a ωωω-=-=用复数表示后，参照（1）可得到加速度频响函数为：∑=+--=-=ni i i i k i s i r s r a rs i kF X H 12)()()(202)21(~~λζλϕϕωω （2） 由公式（2）可知，当k ωω=时，1=k λ，此时式（2）可近似写为：,22)(~)()()()()()(2kk k s k r k k k sk r k k a rs m i k i H ζϕϕζϕϕωωω-=-== （3） 它对应频响函数a rs H ~的幅频曲线的第k 个峰值，其中在上面（3），k m kk k 2()(ω）式中=为各阶主质量．．．n k ,3,2,1=。

改变s 点的位置，在不同点激振，可以得到不同点与点r之间的频响函数，当s=r 时，就可得到点r 处的原点频响函数，表示为：∑=+--=ni i i i i i r i r a rr i k H 12)()()(2)21(~λζλϕϕω （4） 它的第k 个峰值为：,2)(~)()()(2kk k r k r k k a rr k i H ζϕϕωωω-== （5）由（3）/（5）得到：（6）若另1)(=k rϕ，就可得到：（7）由（7）式，另s=1,2,3，．．．．．．ｎ，就可得到第k 阶主振型的各个元素。

工程力学中的悬臂梁受力和弯曲变形问题的分析与计算方法总结悬臂梁是工程力学中常见的结构，其受力和弯曲变形问题一直是研究的焦点。

本文将对悬臂梁受力和弯曲变形问题的分析与计算方法进行总结。

一、悬臂梁的受力分析在工程实践中，悬臂梁常常承受着外部力的作用，因此对其受力进行准确的分析至关重要。

悬臂梁的受力分析主要包括弯矩和剪力的计算。

1. 弯矩的计算悬臂梁在受力时会产生弯矩，弯矩的计算可以通过弯矩方程进行。

弯矩方程是基于力的平衡原理和材料的本构关系推导出来的，通过对悬臂梁上各点的力平衡和材料的应力-应变关系进行分析，可以得到弯矩的表达式。

2. 剪力的计算悬臂梁在受力时还会产生剪力，剪力的计算同样可以通过力的平衡原理和材料的本构关系进行推导。

剪力方程可以通过对悬臂梁上各点的力平衡和材料的剪切应力-剪切应变关系进行分析得到。

二、悬臂梁的弯曲变形分析除了受力分析外，悬臂梁的弯曲变形也是需要考虑的重要问题。

弯曲变形是指悬臂梁在受力作用下产生的弯曲形变，主要表现为悬臂梁的中性面发生偏移和悬臂梁上各点的位移。

1. 弯曲形变的计算弯曲形变的计算可以通过弯曲方程进行。

弯曲方程是基于力的平衡原理和材料的本构关系推导出来的，通过对悬臂梁上各点的力平衡和材料的应力-应变关系进行分析，可以得到弯曲形变的表达式。

2. 中性面的偏移和位移的计算中性面的偏移和位移是悬臂梁弯曲变形的重要表现形式。

中性面的偏移可以通过弯曲方程和几何关系进行计算，位移可以通过位移方程进行计算。

通过这些计算，可以得到悬臂梁上各点的位移和中性面的偏移情况。

三、悬臂梁的计算方法总结为了更准确地分析和计算悬臂梁的受力和弯曲变形问题，工程力学中提出了一系列计算方法。

常见的计算方法包括静力学方法、力学性能方法和有限元方法等。

1. 静力学方法静力学方法是最常用的计算方法之一，它基于力的平衡原理和材料的本构关系进行分析和计算。

通过对悬臂梁上各点的力平衡和材料的应力-应变关系进行分析，可以得到悬臂梁的受力和弯曲变形情况。

北京航空航天大学梁变形实验——简支梁实验实验报告机械工程及自动化学院380711班张涛38071122实验一 梁变形实验——简支梁实验一、实验目的：1、 简支梁在跨度中点承受集中载荷P ，测定梁最大挠度和支点处转角，并与理论值比较；2、 验证位移互等定理；3、 测定简支梁跨度中点受载时的挠曲线（测量数据点不少于7个）。

二、实验设备：4、 简支梁及支座；5、 百分表和磁性表座；6、 砝码、砝码盘和挂钩；7、 游标卡尺和钢卷尺。

三、试件及实验装置：中碳钢矩形截面梁，=s σ360MPa ，E=210GPa 。

图二 实验装置图图一 实验装置简图材料力学实验3 / 7四、实验原理和方法：8、 简支梁在跨度中点承受集中载荷P 时，跨度中点处的挠度最大； 9、 梁小变形时，简支梁某点处的转角atg δθθ=≈)(；10、 验证位移互等定理：对于线弹性体，F 1在F 2引起的位移∆12上所作之功，等于F 2在F 1引起的 位移∆21上所作之功，即：212121∆⋅=∆⋅F F （1）若F 1=F 2，则有：2112∆=∆ （2）上式说明：当F 1与F 2数值相等时，F 2在点1沿F 1方向引起的位移∆12，等于F 1在点2沿F 2方向引起的位移∆21。

此定理称为位移互等定理。

为了尽可能减小实验误差，本实验采用重复加载法，要求重复加载次数n ≥4。

取初载荷P 0=(Q+1)Kgf(Q 为砝码盘和砝码钩的总重量)，∆P=1.5Kgf ，为了防止加力点位置变动，在重复加载过程中，最好始终有0.5Kgf 的砝码保留在砝码盘上。

五、加载方案采用重复加载法，重复加载次数n 4≥，初载荷为1千克， 1.5P kg ∆=图三 位移互等定理示意图六、数据处理 1、原始数据列表 ○1梁的高度及宽度○2选取点2和点5位置加载以验证位移互等定理数据○3在中点加载，测量各点挠度改变量2、数据计算与分析○1中点挠度的理论值与实际值的比较333331294 1.59.8(80010)19.8810.00104848482101012124.507010Fl Pgl BH EI E mω---∆⨯⨯⨯=-=-=-⨯⨯⨯⨯⨯=-⨯中点材料力学实验5 / 7实际值：44.2810m ω-=-⨯实相对误差：4.28 4.5070%100%100% 5.366%4.5070ωωηω--+=⨯=⨯=中点实中点 ○2转角的实际值与理论值的比较332129F 1.5(80010)19.8810.0010161621010120.00169l rad EIradθ--⨯⨯=-=-⨯⨯⨯⨯⨯=-理论实际值：213100.00185770.00rad rad a δθ-∆⨯=-=-=-实 相对误差：0.001690.001857%100%100%9.88%0.00169ωωηω--+=⨯=⨯=理论实实○3验证位移互等定理 有原始数据列表○2中可以看出恰巧2552∆=∆，，，这便验证了位移互等定理○4绘制简支梁受载时的挠曲线（绘图程序见后面附录） 利用实验中的位移互等定理很容易画出挠曲线，如下0.0040.0030.0020.0013、误差分析通过理论值与实际测量值的比较,以及位移互等定理验证的过程中数值的对比,不难看出,误差比较小,实验进行的还是相对准确的.产生误差的原因,我认为有几个方面:○1量的两端没有固定完全,在实验的过程中可能产生微小的移动; ○2加砝码时产生的晃动引入误差; ○3百分表置零时产生的机械误差; ○4在读数过程中,引入随机误差等. 七、 试验后思考题1、 若需要测量简支梁跨度中任意截面处的转角，其实验装置如何？答：为了测出任意处的转角，在此处两侧等距处可加一百分表（a 的值很小）变形后同时读出两个百分表的视数A δ，A'δ，在小变形的条件下，可以认为'arctan 2A Aaδδθθ-==。

本节讨论悬臂梁的弯曲，考察薄板梁，左端固定，右端受切向分布力作用，其合力为F，悬臂梁在力的作用下将产生弯曲。

设梁的跨度为l，高度为h，厚度为一个单位，自重忽略不计。

首先讨论梁的弯曲应力。

对于悬臂梁，建立坐标系如图所示。

则梁的边界条件为该边界条件要完全满足非常困难。

但深入分析发现，只要梁是细长的，则其上下表面为主要边界，这是必须精确满足；而左右端面的边界条件，属于次要边界。

根据圣维南原理，可以使用静力等效的应力分布来替代，这对于离端面稍远处的应力并无实质性的影响。

因此两端面的边界条件可以放松为合力相等的条件。

此外由于梁是外力静定的，固定端的三个反力可以确定，因此在求应力函数时，只要三面的面力边界条件就可以确定。

固定端的约束，即位移边界条件只是在求解位移时才使用。

这样问题的关键就是选择适当的应力函数，使之满足面力边界条件。

因为在梁的上下边界上，其弯矩为F(l-x)，即力矩与(l-x)成正比，根据应力函数的性质，设应力函数为其中f(y)为y的任意函数。

将上述应力函数代入变形协调方程，可得即，积分可得由于待定系数d不影响应力计算，可令其为零。

所以，应力函数为将上述应力函数代入应力分量表达式，可得应力分量返回将上述应力分量代入面力边界条件，可以确定待定系数。

在上下边界，自动满足。

而，则要求在x= l边界上，自动满足。

而，则要求联立求解上述三式，可得注意到对于图示薄板梁，其惯性矩。

所以应力分量为所得应力分量与材料力学解完全相同。

当然对于类似问题，也可以根据材料力学的解答作为基础，适当选择应力函数进行试解，如不满足边界条件，再根据实际情况进行修正。

返回应力分量求解后，可以进一步求出应变和位移。

将应力分量代入几何方程和物理方程，可得对于上述公式的前两式分别对x，y积分，可得其中f（y），g（x）分别为y，x的待定函数。

将上式代入应变分量表达式的第三式，并作整理可得由于上式左边的两个方括号内分别为x，y的函数，而右边却为常量，因此该式若成立，两个方括号内的量都必须为常量。

悬臂梁实验指导一、 实验目的1、 初步掌握电测方法和多点应变测量技术；2、 测定悬臂梁上下表面的应力，验证梁的弯曲理论。

二、 实验设备1、 材料力学组合试验台；2、 电阻应变仪；3、 矩形截面钢梁。

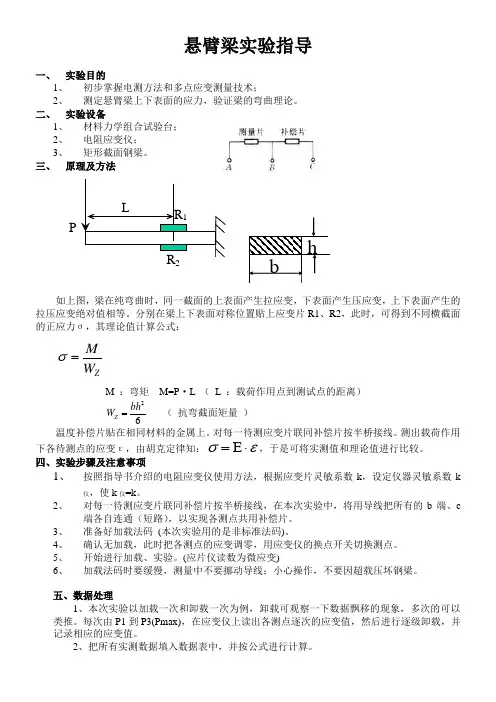
三、 原理及方法如上图，梁在纯弯曲时，同一截面的上表面产生拉应变，下表面产生压应变，上下表面产生的拉压应变绝对值相等。

分别在梁上下表面对称位置贴上应变片R1、R2，此时，可得到不同横截面的正应力σ，其理论值计算公式：ZW M =σM ：弯矩 M=P ·L （L ：载荷作用点到测试点的距离）62bh W Z = （ 抗弯截面矩量 ）温度补偿片贴在相同材料的金属上。

对每一待测应变片联同补偿片按半桥接线。

测出载荷作用下各待测点的应变ε，由胡克定律知：εσ⋅E =，于是可将实测值和理论值进行比较。

四、实验步骤及注意事项1、 按照指导书介绍的电阻应变仪使用方法，根据应变片灵敏系数k ，设定仪器灵敏系数k仪，使k 仪=k 。

2、对每一待测应变片联同补偿片按半桥接线，在本次实验中，将用导线把所有的b 端、c 端各自连通（短路），以实现各测点共用补偿片。

3、 准备好加载法码 (本次实验用的是非标准法码)。

4、 确认无加载，此时把各测点的应变调零，用应变仪的换点开关切换测点。

5、 开始进行加载、实验。

(应片仪读数为微应变)6、 加载法码时要缓慢，测量中不要挪动导线；小心操作，不要因超载压坏钢梁。

五、数据处理1、本次实验以加载一次和卸载一次为例，卸载可观察一下数据飘移的现象，多次的可以类推。

每次由P1到P3(Pmax)，在应变仪上读出各测点逐次的应变值，然后进行逐级卸载，并记录相应的应变值。

2、把所有实测数据填入数据表中，并按公式进行计算。

2P3、每一测点求出测σ对理σ的相对误差e ：%100⨯-=理测理σσσσe4、相关数据应变片灵敏系数k=2，阻值为120Ω； 悬臂梁弹性模量E=2.15×1011 Pa悬臂梁横相关几何尺寸：L=300mm 、h=10mm 、b=30mm 、1N=0.102kgf 1kgf (公斤力) =9.8N1MPa=1×106 Pa (1MPa=1N/mm 2，1Pa=1N/m 2)实验中心 机械实验室 2009年10月。

锤击法测量悬臂梁的固有振动参数试验报告悬臂梁是工程中常用的一种结构形式，在实际应用中，了解悬臂梁的固有振动参数对于设计和分析都非常重要。

锤击法是一种常见的测量悬臂梁固有振动参数的实验方法，本文将通过锤击法测量悬臂梁的固有振动参数，并撰写一份试验报告。

1.实验目的：本实验的目的是采用锤击法测量悬臂梁的固有振动参数，包括固有频率和振动模态。

2.实验设备和材料：-悬臂梁：长度为L的悬臂梁-锤子：质量为m的锤子-支座：用于支撑悬臂梁和固定激振点的支座-多功能振动测试仪：用于采集实验数据和分析振动模态-实验室测量器具：如电子天平、尺子等3.实验步骤：3.1准备工作-准备好悬臂梁和支座，并确保悬臂梁能够在支座上稳定地放置。

-将多功能振动测试仪连接到计算机上，并打开测试软件。

3.2测量固有频率-将锤子在悬臂梁上的不同位置进行轻微的敲击，记录每次敲击的时间和位置。

-根据记录的数据，计算出各个位置的固有频率，即悬臂梁的自由振动频率。

-重复上述操作，至少进行五次测量以获得准确结果。

3.3测量振动模态-在悬臂梁的敏感点上安装合适的加速度计。

-通过多功能振动测试仪采集加速度计的数据，并进行实时分析。

-在分析软件中观察和记录悬臂梁的振动模态，包括节点位置和相应的模态形态。

-重复上述操作，至少进行五次测量以获得准确结果。

4.数据处理与分析：4.1固有频率的计算根据实际测量的数据，可以计算出悬臂梁的固有频率。

根据振动理论，悬臂梁的固有频率与其几何尺寸和材料属性有关，可以使用以下公式计算：fn = αn * sqrt(E/(ρ*L^4))其中，fn为第n个固有频率，αn为与振动模态相对应的常数，E为悬臂梁的杨氏模量，ρ为悬臂梁的质量密度，L为悬臂梁的长度。

4.2振动模态的分析通过振动测试仪采集的振动信号，可以进行振动模态的分析。

根据振动模态的特点，可以确定悬臂梁的节点位置和相应的模态形态。

通过多次测量和分析，可以进一步验证实验结果的准确性。

实验三悬臂梁弯曲变形的测定
一：实验目的
掌握悬臂梁弯曲变形的测定，掌握用电阻应变片的测定应变方法。

二：实验设备及仪表
（1）DH3816静态电阻应变仪；
（2）扭转悬臂梁；
（3）测电阻应变片。

三：实验方法
（1）在扭转悬臂梁上沿轴向准确贴好应变片。

（2）用半桥梁将应变片接入静态电阻应变仪；
（3）给梁逐级加砝码，由给梁所加重量换算出已知应变ε计
（梁的材料弹性模
量已知）；
（4）由应变仪测取每级荷载下的应变值ε仪
记入表格。

一、实验数据处理
测点44
重物2kg
悬臂梁悬臂长度10.5cm
直径34.5mm
到应变花的距离8.5cm。

基于SolidWorks的梁的弯曲变形仿真实验设计
基于SolidWorks的梁的弯曲变形仿真实验设计摘要:应用机械设计软件SolidWorks的COSMOSXpress工具对梁的弯曲变形进行仿真实验,通过对梁进行有限元分析,直观的验证了梁发生弯曲变形时的应力分布与变形规律,为改进梁的结构和优化设计提供了简便易行的有效手段。

关键词:SolidWorks COSMOSXpress 仿真实验应力分析有限元仿真是利用模型复现实际系统中发生的本质过程,并通过对模型的实验来分析研究系统。

仿真与数值计算、求解方法的区别在于它首先是一种实验技术。

仿真实验与物理实验相比,能够极大缩短设计周期,降低设计成本,提高设计效率。

借助计算机仿真对悬臂梁发生弯曲变形进行仿真实验,既可以直观的了解梁的应力分布与变形规律,还能在对其应力分析的基础上进行结构改进和优化设计,为梁的弯曲变形研究提供了简便可靠的有效手段。

1 仿真实验设计思路
仿真的重要工具是计算机和仿真软件。

仿真的过程包括建立仿真模型和进行仿真实验两个主要步骤:即借助三维机械设计软件SolidWorks进行建模,并应用其插件COSMOSXpress工具对模型进行应力分析,真实直观再现梁的弯曲变形物理过程。

comsol仿真实验报告一、实验目的本次实验旨在通过使用 COMSOL Multiphysics 软件对特定的物理现象或工程问题进行仿真分析，深入理解相关理论知识，并获取直观、准确的结果，为实际应用提供有效的参考和指导。

二、实验原理COMSOL Multiphysics 是一款基于有限元方法的多物理场仿真软件，它能够将多个物理场（如电场、磁场、热场、流体场等）耦合在一个模型中进行求解。

其基本原理是将连续的求解区域离散化为有限个单元，通过对每个单元上的偏微分方程进行近似求解，最终得到整个区域的数值解。

在本次实验中，我们所涉及的物理场及相关方程如下：（一）热传递热传递主要有三种方式：热传导、热对流和热辐射。

热传导遵循傅里叶定律：＄q ＝k\nabla T$，其中＄q$ 为热流密度，＄k$ 为热导率，＄＼nabla T$ 为温度梯度。

热对流通过牛顿冷却定律描述：＄q ＝ h(T T_{amb}）＄，其中＄h$ 为对流换热系数，＄T$ 为物体表面温度，＄T_{amb}＄为环境温度。

（二）流体流动对于不可压缩流体，其运动遵循纳维斯托克斯方程：＄＼rho(＼frac{＼partial ＼vec{u}｝｛＼partial t} ＋（＼vec{u}＼cdot\nabla)＼vec{u}）＝＼nabla p ＋＼mu\nabla^2\vec{u} ＋＼vec{f}＄其中＄＼rho$ 为流体密度，＄＼vec{u}＄为流体速度，＄p$ 为压力，＄＼mu$ 为动力粘度，＄＼vec{f}＄为体积力。

（三）电磁场麦克斯韦方程组是描述电磁场的基本方程：＄＼nabla\cdot\vec{D} ＝＼rho$＄＼nabla\cdot\vec{B} ＝ 0$＄＼nabla\times\vec{E} ＝＼frac{＼partial ＼vec{B}｝｛＼partial t}＄＄＼nabla\times\vec{H} ＝＼vec{J} ＋＼frac{＼partial ＼vec{D}｝｛＼partial t}＄其中＄＼vec{D}＄为电位移矢量，＄＼vec{B}＄为磁感应强度，＄＼vec{E}＄为电场强度，＄＼vec{H}＄为磁场强度，＄＼rho$ 为电荷密度，＄＼vec{J}＄为电流密度。

北京航空航天大学、材料力学、实验报告实验名称：梁变形实验学号 39051210姓名 齐士杰实验时间：2011.3.7 试件编号试验机编号 计算机编号 应变仪编号百分表编号成绩实验地点：主楼南翼116室- - - - -教师2011年3月14日一、 实验目的：1、用悬臂梁测应变的方法测定未知砝码的重量；2、验证位移互等定理；3、测定简支梁跨度中点受载时的挠曲线（测量数据点不少于7个）;4、简支梁在跨度中点承受集中载荷P ，测定梁最大挠度和支点处转角，并与理论值比较。

二、 实验设备：1、简支梁、悬臂梁及支座；2、百分表和磁性表座；3、砝码、砝码盘和挂钩；4、游标卡尺和钢卷尺。

三、 试件及实验装置：中碳钢矩形截面梁，=s σ360MPa ，E=210GPa 。

图二 实验装置图 四、 实验原理和方法： （1）悬臂梁实验根据梁的弯曲正应力公式及应力应变公式得：ZW E M∙=ε，即为实验理论基础。

（2）简支梁实验1、简支梁在跨度中点承受集中载荷P 时，跨度中点处的挠度最大；2、梁小变形时，简支梁某点处的转角atg δθθ=≈)(；3、验证位移互等定理：θf maxP图一 实验装置简图δaF 112∆12F 2 1 2对于线弹性体，F 1在F 2引起的位移∆12上所作之功，等于F 2在F 1引起的 位移∆21上所作之功，即：212121∆⋅=∆⋅F F （1）若F 1=F 2，则有：2112∆=∆ （2）上式说明：当F 1与F 2数值相等时，F 2在点1沿F 1方向引起的位移∆12，等于F 1在点2沿F 2方向引起的位移∆21。

此定理称为位移互等定理。

五、实验数据及处理： （1）悬臂梁实验：B=12.78mm H=6.79mm G=210Gpa g=9.8m/s 2公式gLEW m zε=计算如下表：编号 1 2 3 4 5 6 ε(10-6) 19 51 83 116 145 179 L(mm) 65.6 165.6 265.6 365.6 465.6 565.6 m(g) 300.93323.57 329.16 323.98 333.14334.07m 平均(g)319.7称量得知，位置砝码重量310g ，计算的相对误差3.1%（2）简支梁实验图三 位移互等定理示意图B=20.10mm H=9.00mm G=210Gpa g=9.8m/s 2（a ）验证位移互等定理加载位置 测量位置 加载重量（kg ） 百分表读数中点 81.531.6 8 中点 31.2 1 中点1.516.4 中点 418.0进行了2组加载和测量，基本符合位移互等定理的内容。

CAE悬臂梁静力分析实验报告实验报告：CAE悬臂梁静力分析摘要本实验主要通过使用CAE软件进行悬臂梁的静力分析，研究其受力情况和变形特点。

通过建立悬臂梁的有限元模型并施加加载条件，得到了悬臂梁的应力分布和变形情况。

实验结果表明，在给定的加载条件下，悬臂梁在受力过程中产生了较大的应力和变形。

引言悬臂梁是一种常见的结构形式，在工程中应用广泛。

为了研究悬臂梁的受力和变形情况，本实验选取CAE软件进行静力分析。

通过建立悬臂梁的有限元模型并施加加载条件，我们可以得到悬臂梁的应力分布和变形情况，为工程实际应用提供参考。

实验设计1.建立模型：首先，在CAE软件中根据悬臂梁的尺寸参数和材料属性建立有限元模型。

通常可以将悬臂梁简化为一维杆件模型，并在模型中加入支撑和加载条件。

2.施加加载条件：在模型中施加加载条件，例如在悬臂梁的一端施加一个集中力，以模拟实际工程中的受力情况。

3.网格剖分：对模型进行网格剖分，将其分解成若干个小单元，以便进行有限元计算。

4.设置材料属性：确定材料的弹性模量和泊松比等参数，用于计算应力和变形。

5.分析计算：使用有限元分析方法进行计算，得到悬臂梁在受力过程中的应力分布和变形情况。

6.结果分析：对计算结果进行分析，确定悬臂梁受力和变形的特点，并与理论分析进行比较。

实验结果根据实验设计的步骤，我们成功建立了悬臂梁的有限元模型，并施加了加载条件。

在进行有限元计算后，我们得到了悬臂梁在受力过程中的应力分布和变形情况。

在加载条件下，悬臂梁的一端受到了集中力的作用，导致了悬臂梁在该点附近产生了较大的应力。

应力沿着悬臂梁的长度呈现递减的趋势，且在悬臂梁的受力端附近达到了最大值。

此外，加载条件还导致了悬臂梁的变形。

悬臂梁在受力端附近产生了较大的弯曲变形，并逐渐向悬臂梁的自由端变形。

变形随着距离受力端的增加而递减。

结果分析根据实验结果，我们可以得出以下结论：1.悬臂梁在受力过程中产生了较大的应力，应特别关注悬臂梁受力端附近的应力集中情况。

悬臂梁的振动模态实验报告悬臂梁是一种常见的结构，广泛应用于工程中。

在实际应用中，悬臂梁的振动特性是非常重要的，因为它会对悬臂梁结构的稳定性和安全性产生影响。

因此，了解悬臂梁的振动模态是一项必要的研究任务。

本次实验旨在通过实验方法测量和分析悬臂梁的振动模态，并探究不同参数对振动模态的影响。

实验过程中使用的设备和仪器包括悬挂系统、激励源、传感器、数据采集系统等。

实验步骤如下：1.悬挂梁结构：将悬挂系统固定在实验室的支架上，确保悬臂梁能够在完全自由的情况下自由振动。

2.激励源：将激励源与悬挂梁连接，通过激励源提供外力。

3.传感器：在悬臂梁上选择合适的位置安装传感器，用于测量悬臂梁的振动信号。

4.数据采集系统：将传感器与数据采集系统相连，用于实时采集和记录振动信号。

5.实施实验：通过激励源提供激励力，使悬臂梁产生振动，并同时记录悬挂梁的振动信号。

6.数据处理：通过数据采集系统获得的数据，使用相应的信号处理技术对振动信号进行处理，得到振动模态的相关参数。

7.结果分析：根据实验结果，分析悬臂梁的振动特性和模态，并探究不同参数对振动模态的影响。

通过以上实验步骤，我们可以获得悬臂梁的振动模态，并了解不同参数对振动模态的影响。

实验结果有助于工程设计中的结构设计和改进。

在实验过程中，我们还需要注意以下几个方面的问题：1.悬挂系统的稳定性和刚度：确保悬挂系统能够提供稳定的支撑，并且具有足够的刚度，以保证悬臂梁在振动过程中不会产生偏差。

2.激励源的选取：根据实际需求和悬臂梁的特性，选择合适的激励源，以提供适当的激励力。

3.传感器的准确性：选择合适的传感器，并保证传感器的准确性和灵敏度，以获得准确的振动信号。

4.数据采集和处理的准确性：使用合适的数据采集系统和信号处理技术，以保证数据采集和处理的准确性。

总之，通过本次实验，我们可以深入了解悬臂梁的振动模态，并探究不同参数对振动模态的影响。

这对于工程设计和结构改进具有重要意义，可以提高悬臂梁结构的稳定性和安全性。