大变形问题的有限元分析
- 格式：ppt
- 大小：384.50 KB
- 文档页数：27
文档推荐
-
有限元分析保险杠1页数:7
-
铆钉材料对铆接变形影响的有限元分析页数:3
-
仿真分析技术在重型运载火箭舱段铆接装配中 的应用页数:10
下载文档原格式
合集下载
有限元分析FEA
广州有道计算机科技有限公司有限元分析FEA有限元法（FEA，Finite Element Analysis）的基本概念是用较简单的问题代替复杂问题后再求解。
它将求解域看成是由许多称为有限元的小的互连子域组成，对每一单元假定一个合适的(较简单的）近似解，然后推导求解这个域总的满足条件(如结构的平衡条件），从而得到问题的解。
这个解不是准确解，而是近似解，因为实际问题被较简单的问题所代替。
由于大多数实际问题难以得到准确解，而有限元不仅计算精度高，而且能适应各种复杂形状，因而成为行之有效的工程分析手段。
有限元分析（FEA，Finite Element Analysis）利用数学近似的方法对真实物理系统（几何和载荷工况）进行模拟。
还利用简单而又相互作用的元素，即单元，就可以用有限数量的未知量去逼近无限未知量的真实系统。
大型通用有限元商业软件：如ANSYS可以分析多学科的问题，例如：机械、电磁、热力学等；电机有限元分析软件NASTRAN等。
还有三维结构设计方面的UG、CATIA、Proe等都是比较强大的。
国产有限元软件：FEPG、SciFEA、,JiFEX、KMAS等有限元法：把求解区域看作由许多小的在节点处相互连接的单元（子域）所构成，其模型给出基本方程的分片（子域）近似解，由于单元（子域）可以被分割成各种形状和大小不同的尺寸，所以它能很好地适应复杂的几何形状、复杂的材料特性和复杂的边界条件。
有限元方法的基础是变分原理和加权余量法，其基本求解思想是把计算域划分为有限个互不重叠的单元，在每个单元内，选择一些合适的节点作为求解函数的插值点，将微分方程中的变量改写成由各变量或其导数的节点值与所选用的插值函数组成的线性表达式，借助于变分原理或加权余量法，将微分方程离散求解。
采用不同的权函数和插值函数形式，便构成不同的有限元方法。
有限元法的收敛性是指：当网格逐渐加密时，有限元解答的序列收敛到精确解；或者当单元尺寸固定时，每个单元的自由度数越多，有限元的解答就越趋近于精确解。
有限元实例分析
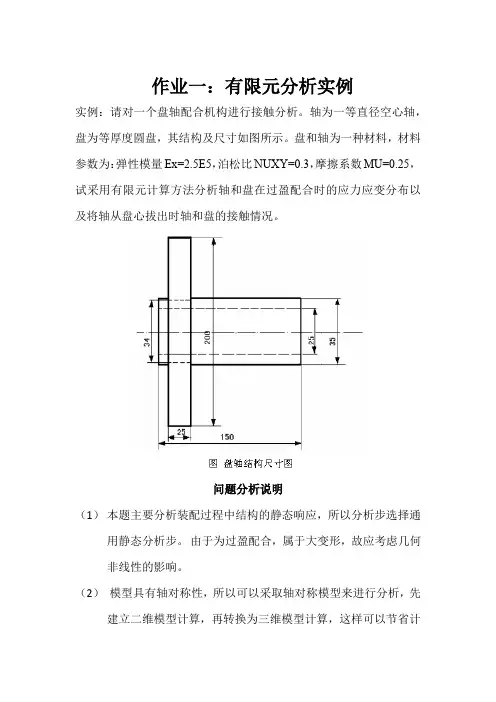
作业一：有限元分析实例实例：请对一个盘轴配合机构进行接触分析。
轴为一等直径空心轴，盘为等厚度圆盘，其结构及尺寸如图所示。
盘和轴为一种材料，材料参数为：弹性模量Ex=2.5E5，泊松比NUXY=0.3，摩擦系数MU=0.25，试采用有限元计算方法分析轴和盘在过盈配合时的应力应变分布以及将轴从盘心拔出时轴和盘的接触情况。
问题分析说明（1）本题主要分析装配过程中结构的静态响应，所以分析步选择通用静态分析步。
由于为过盈配合，属于大变形，故应考虑几何非线性的影响。
（2）模型具有轴对称性，所以可以采取轴对称模型来进行分析，先建立二维模型计算，再转换为三维模型计算，这样可以节省计算时间。
分析过程由两个载荷步组成, 第一个载荷步为过盈分析, 求解过盈安装时的情况。
第二个载荷步为将轴从盘心拔出时的接触分析, 分析在这个过程中盘心面和轴的外表面之间的接触应力。
它们都属于大变形问题, 属于非线性问题。
在分析时需要定义一些非线性选项来帮助问题的收敛。
（3）接触面之间有很大的相对滑动，所以模型要使用有限滑移。
模型建立的分析说明（1）进定义单元类型此项实例分析的问题中涉及到大变形, 故选用So li d185 单元类型来建立本实例入部件模块，的模型。
盘轴接触问题属于面面接触, 目标面和接触面都是柔性的,将使用接触单元T ARGET 170 和CO NTAT17 4来模拟接触面。
分别创建名为为part1、part2的部件。
（2）定义材料属性，在线性各向同性材料属性对话框中的EX (弹性模量) 文本框中输入 2 . 5E5,PRX Y (泊松比) 文本框中输入0 . 3,并将定义的材料属性赋予给part1和part2。
如下图所示。
（3）进入装配模块，创建两者间的装配关系。
（4）进入分析步模块定义名为step1和step2的两个分析步。
（5）进入相互作用模块，创建相互作用属性，设置摩擦系数；然后定义接触关系。
如下图所示。
（6）进入载荷模块，创建边界条件，依次定义名为BC -2（类型为：完全固定）、BC -3（类型为：位移/转角，约束U1、UR3），分析步均为Initial 。
有限元分析1
有限单元法的形成与发展
我国的力学工作者为有限元方法的初期发展做出了许多贡献，其 中比较著名的有：陈伯屏（结构矩阵方法），钱令希（余能原理）， 钱伟长（广义变分原理），胡海昌（广义变分原理），冯康（有限 单元法理论）。遗憾的是，从1966年开始的近十年期间，我国的研究 工作受到阻碍。
有限元法不仅能应用于结构分析，还能解决归结为场问题的工程 问题，从二十世纪六十年代中期以来，有限元法得到了巨大的发展， 为工程设计和优化提供了有力的工具。
根据结点的平衡条件，得
( Fxie ) FLxi å e ( Fxje ) FLyi å e
e
单元e的结点力，用结点位移表示，代入得到用结点位移 表示的平衡方程。 K FL 单元综合的目的就是要求出结点位移。结点位移求出后， 可进一步求出各单元的应力。
3 单元位移函数
2 有限单元法的计算步骤
弹性力学平面问题的有限单元法包括三个主要步骤： 1、离散化 2、单元分析 3、单元综合
¼ Í
2-7
2 有限单元法的计算步骤
1、离散化 有限单元法的基础是用所谓有限个单元的集合体 来代替原来的连续体，因而必须将连续体简化为由 有限个单元组成的离散体。对于平面问题，最简单， 因而最常用的单元是三角形单元。这些单元在结点 处用铰相连，荷载也移置到结点上，成为结点荷载。
有限单元法的形成与发展
第二类问题，通常可以建立它们应遵循的基本方程，即微分方程 和相应的边界条件。例如弹性力学问题，热传导问题，电磁场问题 等。由于建立基本方程所研究的对象通常是无限小的单元，这类问 题称为连续系统。 尽管已经建立了连续系统 的基本方程，由于边界条件 的限制，通常只能得到少数 简单问题的精确解答 。对于 许多实际的工程问题 ，还无 法给出精确的解答，例如图 示V6引擎在工作中的温度分 布。为解决这个困难 ，工程 师们和数学家们提出了许多 近似方法。
ANSYS大变形预应力模态分析
ANSYS大变形预应力模态分析(2012-08-21 10:49:31)转载▼分类：有限元软件-ansysANSYS大变形预应力模态分析一、原理大变形预应力模态分析用于计算高度变形后结构的固有频率和振型，即在荷载作用下，结构的变形非常大(考虑几何非线性影响)，需要考虑结构变形及其应力对固有频率和振型的影响。
此时的模态分析与预应力模态分析过程基本相同，但特征值的求解用PSOLVE命令而不是SOLVE。
二、分析步骤1、建模同常规建模2、静力分析/SOLantype,static !定义静力分析NLGEOM,ON ！打开大变形效应PSTRES,ON ！打开预应力效应（某些情况下使用SSTIF,ON可帮助收敛）EMATWRITE,YES ！写出EMAT文件，这是PSOLVE求解所必须的文件.......SOLVEFINISH3、模态分析/SOLantype,modal !定义模态分析UPCOORD,1,ON ！修正坐标以得到正确的应力，同时将位移清零！！！！Modifies the coordinates of the active set of nodes, based on the current displacements. PSTRES,ON ！打开预应力效应（某些情况下使用SSTIF,ON可帮助收敛）MODOPT.....MXPAND.....PSOLVE,EIGxxxx !求解特征值（频率）和特征向量（振型）等。
！！！可采用与MODOPT命令相匹配的EIGLANB,EIGFULL,EIGUNSYM,EIGDAMP等。
FINISH4、模态扩展/SOLEXPASS,ON !指定模态扩展PSOLVE,EIGEXP ！特征向量扩展（振型）FINISH三、算例以前面已分析的悬臂梁为例，在恳臂端作用一6000kN的轴向压力和1000kN的竖向力，对该结构进行大变形预应力模态分析。
从分析结果可知，一般模态分析、预应力模态分析、大变形预应力模态分析的一阶频率为分别为6．982HZ、1．967HZ、4．774HZ，可见存在较大的差别。
ABAQUS中橡胶大变形问题的一些解决办法
ABAQUS中橡胶大变形问题的一些解决办法zhangleilyl（搜索论坛的答复以及一些参考书和文献总结，由于水平有限，不免会有很多错误，仅供参考）密封橡胶的数值仿真是一类典型的非线性问题，牵涉到材料非线性（超弹性）、边界非线性（接触）和几何非线性（大变形）问题的集合，如果设置不当，极容易导致求解困难。
特别是在密封橡胶的变形复杂，比如和多个不规则边界接触、变形很大等情况，需要更谨慎的设置相关参数，以求得到合适的解答。
模型的适当简化对薄板问题可忽略厚度方向的应力，作为平面应力（plane stress）问题；对长柱体可忽略第三方向的应变，作为平面应变（plane strain）问题;对O型圈等可作为轴对称问题。
平面应力和平面应变在建立part时需选中2D Planar，轴对称问题需选中Axisymmetric；在选择单元时也应注意三者的区别（CPS* ,CPE*, CAX* ）。
求解器的选择因为问题复杂，使用Standard求解容易不收敛，在精度允许的情况下，可选用Explicit求解器。
只是多数时候Explicit求解时间较长。
应当知道的是，对于橡胶这种典型的不可压缩材料，使用杂交单元（含字母H）是恰当的，但Explicit中没有杂交单元（庄茁书中的例子选用减缩单元）。
并且在Explicit 中，橡胶材料默认泊松比为0.475。
材料模型的选择我只用过其中三个，Neo-hookean，简单易用，就一个参数。
对于初学者和简单的模拟比较方便。
但是当变形增加到一定范围就不能得到准确的结果了，因为它的参数是来自小变形部分的应力-应变关系。
Mooney-Rivlin 是比较常用的本构模型。
对于没有加碳黑的橡胶来说，这模型能得到比较准确的结果。
但是用它来模拟加了碳黑的橡胶就不太精确了。
Yeoh 是用来模拟加碳黑后的橡胶，三个参数都比较容易得到。
可是这个模型在小变形 extension ratio<1.5时结果不准确。
有限元分析与应用详细例题
《有限元分析与应用》详细例题试题1:图示无限长刚性地基上的三角形大坝，受齐顶的水圧力作用，试用三节点常单元和六节点三角形单元对坝体进行有限元分析，并对以下儿种计算方案进行比较：1）分别采用相同单元数LI的三节点常应变单元和六节点三角形单元计算；2）分别釆用不同数量的三节点常应变单元计算；3）当选常应变三角单元时，分别采用不同划分方案计算。
一.问题描述及数学建模不同勿份方案翩无限长的刚性地基上的三角形大坝受齐顶的水压作用可看作一个平面问题，简化为平面三角形受力问题，把无限长的地基看着平面三角形的底边受固定支座约束的作用，受力面的受力简化为受均布载荷的作用。
二・建模及计算过程1.分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算下面简述三节点常应变单元有限元建模过程（其他类型的建模过程类似）:进入ANSYS【开始】f【程序】fANSYS -►ANSYS Product Launcher -^change the working directory -►JobName: shitil-^Run设置计算类型ANSYS Main Menu: Preferences -^select Structural f OK选择单元类型单元是三节点常应变单元，可以用4节点退化表示。
ANSYS MainMenu: Preprocessor -►Element Type-*Add/Edit/Delete -►Add -^select Solid Quad 4 node 42 f OK (back to Element Types window) f Options... -^-select K3: Plane Strainf OKf Close (the Element Type window)定义材料参数材料为钢，可查找钢的参数并在有限元中左义，其中弹性模ME=210Gpa,泊松比vtANSYS Main Menu: Preprocessor f Material Props -►Material Models -►Structural -^Linear f Elastic f Isotropic f input EX:，PRXY: f OK生成几何模型生成特征点ANSYS Main Menu: Preprocessor —Modeling Create -*Keypoints ~*ln Active CS —依次输入四个点的坐标:input:l{0/0)/2(3/0)/3(6,0)/4(3/5)/5(0,10)/6(0/5)-*OK生成坝体截而ANSYS Main Menu: Preprocessor Modeling -*Create -*Areas -►Arbitrary -►Through KPS f 依次连接126;234;246;456这三个特征点一OK网格划分ANSYS Main Menu: Preprocessor f Meshing -►Mesh Toolf ⑸ze Controls) Global: Set -►inputNDIV: I-*OK f (back to the mesh tool window)Mesh: Areas, Shape: Tri, Free -*Mesh f Pick All (inPicking Menu) f Close( the Mesh Tool window)模型施加约束分别给下底边和竖直的纵边施加x和y方向的约朿ANSYS Main Menu: Solution Define Loads Apply f Structural -^Displacement f On lines f 选择底边f OK ->select:ALL DOF f OK给斜边施加x方向的分布载荷ANSYS命令菜单栏:Parameters -^Functions -*Define/Edit -*1）在卜方的卜拉列表框内选择x，作为设麗的变量：2）在Result窗口中岀现{X},写入所施加的载荷函数：1000*{X}；3） File>Save（文件扩展洛：func）f 返回：Parameters f Functions -►Read from file；将需要的・func 文件打开，任给一个参数名，它表示随之将施加的载荷f OK -^ANSYS Main Menu: Solution -►Define Loads —Apply f Structural -►Pressure -►On Lines f 拾取斜边：OK f 在下拉列表框中，选择：Existing table （来自用户定义的变量）f OK -选择需要的载荷参数名一OK分析计算ANSYS Main Menu: Solution -►Solve -^Current LS -*OK(to close the solve Current Load Step window) f OK结果显示确左当前数据为最后时间步的数拯ANSYS Main Menu: General Postproc -►Read Resultf Last Set 查看在外力作用下的变形ANSYS Main Menu: General Postproc —Plot Results Deformed Shape-* select Def + Undeformed f OK 查看节点位移分布情况Contour Plot -*Nodal Solu..・-^select: DOF solution->Displacement vctor sum-^Def + Undeformed f OK 查看节点应力分布情况Contour Plot f Nodal Solu... f select: Stress-*-XY shear stress-*- Def + Undeformed-^OK退出系统ANSYS Utility Menu: File-* Exit...-* Save Everything-*OK三.结果分析三节点常应变单元（6个节点，4个单元）儿何模型图ANOCT 10 201016：46：1€变形图，节点位移图，节点应力图，节点应变图3TEP-1 SUB -：TDC-l ANOCT 10 SCIOx&：2i：ieKO SAX SCLTriSRSUB -1TDE-175TU IX79-. 2SY3-03MX -.109E-3&AN81 10 N101^:22:40.UL£-0«■'aE'>铃"侥六节点常应变单元（6个节点，4个单元） 儿何模型图变形图，节点位移图，节点应力图，节点应变图■QQM r -r~：：r MCAL acunzoc5TT5-：SUB "I T2C-：rrTCKY ap MYfl-3 :«x ・.i03«-nRO» -.M<s-3T n<x -.ioez-oeANOCT 10 Z010.444Z-3： .MM-3? .0Z»E ・S . lOGZ^Ciwr-^iANOCT 10 20103«F-1 an .1 TDX-l na «.:ex-» ANon io RiorniMMKOU ：Ct7T ：：f MIX•： nxE-i i*n> FSY3-)Mi ..”《CV6 x •.jex -^sKXANon 10 K101；.：---.仇.liiC-»S.1)31^5.；5：£-35•wu -w・，““T9inc-n・ WH -P >分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算结果比较单元划分方案变形大小应力大小应变大小值的比较分析■9三节点三角形单元DMX:SMX:DMX:SMN:2778SMX:8749DMX:SMN:SMX:1.最大变形值小：12.最大应力值小；3.最大应变值小。
有限元法及应用课件
13
载荷
节点: 空间中的坐标位置，具有 一定相应，相互之间存在物理 作用。 单元: 节点间相互作用的媒介， 用一组节点相互作用的数值矩阵 描述（称为刚度或系数矩阵)。
载荷
有限元模型由一些简单形状的单元组成，单 元之间通过节点连接，并承受一定载荷。
14
对于一个具体的工程结构，单元的划分越小， 求解的结果就越精确，同时，其计算工作量也就越 大。 梯子的有限元模型不到100个方程；
34
3）非线性边界 在加工、密封、撞击等问题中，接触和摩擦 的作用不可忽视，接触边界属于高度非线性边界。 平时遇到的一些接触问题，如齿轮传动、冲 压成型、轧制成型、橡胶减振器、紧配合装配等， 当一个结构与另一个结构或外部边界相接触时通 常要考虑非线性边界条件。 实际的非线性可能同时出现上述两种或三种 非线性问题。
10
2.几个基本概念 1）单元（element） 将求解的工程结构看成是 由许多小的、彼此用点联结的 基本构件如杆、梁、板和壳组 成的，这些基本构件称为单元。 在有限元法中，单元用一 组节点间相互作用的数值和矩 阵（刚度系数矩阵）来描述。
11
单元具有以下特征：
每一个单元都有确定的方程来描述在一定载荷 下的响应； 模型中所有单元响应的“和”给出了设计的总 体响应； 单元中未知量的个数是有限的，因此称为“有
限单元”。
12
2）节点（node） 单元与单元之间的联结点，称为节点。在有 限元法中，节点就是空间中的坐标位置，它具有 物理特性，且存在相互物理作用。 3）有限元模型（node） 有限元模型真实系统理想化的数学抽象。由 一些形状简单的单元组成，单元之间通过节点连 接，并承受一定载荷。 每个单元的特性是通过一些线性方程式来描 述的。作为一个整体，所有单元的组合就形成了 整体结构的数学模型。
载荷
节点: 空间中的坐标位置，具有 一定相应，相互之间存在物理 作用。 单元: 节点间相互作用的媒介， 用一组节点相互作用的数值矩阵 描述（称为刚度或系数矩阵)。
载荷
有限元模型由一些简单形状的单元组成，单 元之间通过节点连接，并承受一定载荷。
14
对于一个具体的工程结构，单元的划分越小， 求解的结果就越精确，同时，其计算工作量也就越 大。 梯子的有限元模型不到100个方程；
34
3）非线性边界 在加工、密封、撞击等问题中，接触和摩擦 的作用不可忽视，接触边界属于高度非线性边界。 平时遇到的一些接触问题，如齿轮传动、冲 压成型、轧制成型、橡胶减振器、紧配合装配等， 当一个结构与另一个结构或外部边界相接触时通 常要考虑非线性边界条件。 实际的非线性可能同时出现上述两种或三种 非线性问题。
10
2.几个基本概念 1）单元（element） 将求解的工程结构看成是 由许多小的、彼此用点联结的 基本构件如杆、梁、板和壳组 成的，这些基本构件称为单元。 在有限元法中，单元用一 组节点间相互作用的数值和矩 阵（刚度系数矩阵）来描述。
11
单元具有以下特征：
每一个单元都有确定的方程来描述在一定载荷 下的响应； 模型中所有单元响应的“和”给出了设计的总 体响应； 单元中未知量的个数是有限的，因此称为“有
限单元”。
12
2）节点（node） 单元与单元之间的联结点，称为节点。在有 限元法中，节点就是空间中的坐标位置，它具有 物理特性，且存在相互物理作用。 3）有限元模型（node） 有限元模型真实系统理想化的数学抽象。由 一些形状简单的单元组成，单元之间通过节点连 接，并承受一定载荷。 每个单元的特性是通过一些线性方程式来描 述的。作为一个整体，所有单元的组合就形成了 整体结构的数学模型。
Lagrange、Euler、ALE三种方法的简单介绍
Lagrange、Euler、ALE三种方法的简单介绍ALE、Lagrange、Euler是数值模拟中处理连续体的广泛应用的三种方法。
Lagrange方法多用于固体结构的应力应变分析，这种方法以物质坐标为基础，其所描述的网格单元将以类似“雕刻”的方式划分在用于分析的结构上，即是说采用Lagrange方法描述的网格和分析的结构是一体的，有限元节点即为物质点。
采用这种方法时，分析结构的形状的变化和有限单元网格的变化完全是一致的（因为有限元节点就为物质点），物质不会在单元与单元之间发生流动。
这种方法主要的优点是能够非常精确的描述结构边界的运动，但当处理大变形问题时，由于算法本身特点的限制，将会出现严重的网格畸变现象，因此不利于计算的进行。
Euler方法以空间坐标为基础，使用这种方法划分的网格和所分析的物质结构是相互独立的，网格在整个分析过程中始终保持最初的空间位置不动，有限元节点即为空间点，其所在空间的位置在整个分析过程始终是不变的。
很显然由于算法自身的特点，网格的大小形状和空间位置不变，因此在整个数值模拟过程中，各个迭代过程中计算数值的精度是不变的。
但这种方法在物质边界的捕捉上是困难的。
多用于流体的分析中。
使用这种方法时网格与网格之间物质是可以流动的。
ALE方法最初出现于数值模拟流体动力学问题的有限差分方法中。
这种方法兼具Lagrange方法和Euler方法二者的特长，即首先在结构边界运动的处理上它引进了Larange方法的特点，因此能够有效的跟踪物质结构边界的运动；其次在内部网格的划分上，它吸收了Euler 的长处，即是使内部网格单元独立于物质实体而存在，但它又不完全和Euler网格相同，网格可以根据定义的参数在求解过程中适当调整位置，使得网格不致出现严重的畸变。
这种方法在分析大变形问题时是非常有利的。
使用这种方法时网格与网格之间物质也是可以流动的。
固体结构分析中一般都选用lagrange坐标，实际上lagrange euler法在有限元中体现的节点意义正如楼主所述，但是本质牵扯的是参考什么样的坐标来描述应力应变关系。
有限元分析基础PPT课件
11
.
12
.
13
.
14
有限元分析过程的概要
• 本课题先通过一个简单的实例，采用直接 的推导方法，逐步展示有限元分析的基本 流程，从中可以了解有限元方法的思路形 成过程，以及如何由具体的求解步骤归纳 出一种通用的标准求解方法。
.
15
有限元分析的目的和概念
• 任何具有一定使用功能的构件(称为变形体)都是 由满足要求的材料所制造的，在设计阶段，就需 要对该构件在可能的外力作用下的内部状态进行 分析，以便核对所使用材料是否安全可靠，以避 免造成重大安全事故。描述可承力构件的力学信 息一般有三类： (1) 构件中因承载在任意位置上所引起的移动(称 为位移)； (2) 构件中因承载在任意位置上所引起的变形状态 (称为应变)； (3) 构件中因承载在任意位置上所引起的受力状态 (称为应力)；
时系统研究了离散杆、梁、三角形的单元刚度
.
5
表达式；1960年Clough在处理平面弹性问题，第一
次提出并使用“有限元方法” 的名称；1955年德国
的Argyris出版了第一本关于结构分析中的能量原理
和矩阵方法的书，为后续的有限元研究奠定了重要
的基础，1967年Zienkiewicz和Cheung出版了第一
也就是产生了78个受力区域，在钢结构焊接完成后，
需要将其缓慢而又平稳地卸去，让鸟巢变成完全靠
自身结构支撑；
.
9
因而，支撑塔架的卸载，实际上就是对整个钢 结构的加载，如何卸载？需要进行非常详细的数值 化分析，以确定出最佳的卸载方案。2006年9月17 日成功地完成了整体钢结构施工的最后卸载。
.
10
.
.
4
20世纪40年代，由于航空事业的飞速发展，设计
第一节 有限元分析概述
第一节 有限元分析概述对于一般的工程受力问题，希望通过平衡微分方程、变形协调方程、几何方程和本构方程联立求解而获得整个问题的精确解是十分困难的，一般几乎是不可能的。
随着20世纪五六十年代计算机技术的出现和发展、以及工程实践中对数值分析要求的日益增长，并发展起来了有限元的分析方法。
有限元法自1960年由Clough首次提出后，获得了迅速的发展；虽然首先只是应用于结构的应力分析，但很快就广泛应用于求解热传导、电磁场、流体力学、成形工艺等连续问题。
一、有限元法的基本概念对于连续体的受力问题，既然作为一个整体获得精确求解十分困难；于是，作为近似求解，可以假想地将整个求解区域离散化，分解成为一定形状有限数量的小区域（即单元），彼此之间只在一定数量的指定点（即节点）处相互连接，组成一个单元的集合体以替代原来的连续体，如图7-1弯曲凹模的受力分析所示；只要先求得各节点的位移，即能根据相应的数值方法近似求得区域内的其他各场量的分布；这就是有限元法的基本思想。
从物理的角度理解，即将一个连续的凹模截面分割成图7-1所示的有限数量的小三角形单元，而单元之间只在节点处以铰链相连接，由单元组合成的结构近似代替原来的连续结构。
如果能合理地求得各单元的力学特性，也就可以求出组合结构的力学特性。
于是，该结构在一定的约束条件下，在给定的载荷作用下，各节点的位移即可以求得，进而求出单元内的其他物理场量。
这就是有限元方法直观的物理的解释。
从数学角度理解，是将图7-1所示的求解区域剖分成许多三角形子区域，子域内的位移可以由相应各节点的待定位移合理插值来表示。
根据原问题的控制方程（如最小势能原理）和约束条件，可以求解出各节点的待定位移，进而求得其他场量。
推广到其他连续域问题，节点未知量也可以是压力、温度、速度等物理量。
这就是有限元方法的数学解释。
从有限元法的解释可得，有限元法的实质就是将一个无限的连续体，理想化为有限个单元的组合体，使复杂问题简化为适合于数值解法的结构型问题；且在一定的条件下，问题简化后求得的近似解能够趋近于真实解。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 大变形问题的有限元分析
目的：以大变形问题为例， 目的：以大变形问题为例，介绍几何非线性问题的有限元 方法。 方法。 特点：与线性有限元方法比较，几何关系不再是线性的。 特点：与线性有限元方法比较，几何关系不再是线性的。 内容： 内容： 引言 大变形问题的应变描述 大变形分析中的应力描述及本构关系 大变形问题有限元方程的建立 大变形分析中的载荷处理 小结
11
2011-10-19
现时构型时材料的密 随变形变化。 度－随变形变化。
大变形分析中的本构关系(4/5) 大变形分析中的本构关系(4/5)
次弹性材料 若应力率与变形率之间成线性变化规律，这类材料称为次弹性材料。但 应力率与变形率之间成线性变化规律，这类材料称为次弹性材料。 之间成线性变化规律 本构关系描述时要求“ 为与刚体转动无关的客观时间导数。 本构关系描述时要求“率”为与刚体转动无关的客观时间导数。
本构关系的客观性要求：需要选取合适的应力－ 本构关系的客观性要求：需要选取合适的应力－应变共轭对 描述材料的本构关系。 描述材料的本构关系。 弹性材料：加载曲线与卸载曲线相同的材料。 弹性材料：加载曲线与卸载曲线相同的材料。
，
本构关系有三种形式
σ ij = Aijkl ε kl
∂W σ ij = ∂ε ij
初始构型时材料 的密度－ 的密度－常数 Case-2
* W = W ( ε ij )
* ∂ ρ *W ( ε kl ) * Sij = * ∂ε ij
≜ AIJKLε KL
相 比 较
坐标变换
一阶近似
总之， 总之，对于一般的大变形 问题， 问题，在连续介质力学中 不能简化！ 不能简化！ 常用超弹性来表征材料的 本构关系。 本构关系。
初始构型（ 时刻 时刻） 初始构型（0时刻）
现时构型（ 时刻） 现时构型（t 时刻）
当前构型（ 时刻） 当前构型（ t + ∆t 时刻）
连续介质力学理论对物体经历大变形后的变形有严格的定义 连续介质力学理论对物体经历大变形后的变形有严格的定义 和推导。这里不准备过多引入复杂的概念和符号， 和推导。这里不准备过多引入复杂的概念和符号，而是与小变形 理论对照，介绍进行大变形分析时必需的几个概念和术语。 理论对照，介绍进行大变形分析时必需的几个概念和术语。
特殊情形
S IJ = AIJKLε KL
不依赖于构型变化 弹性本构关系多用于大位移（转动）小应变的情形。 弹性本构关系多用于大位移（转动）小应变的情形。 大位移 的情形
2011-10-19
10
大变形分析中的本构关系(3/5) 大变形分析中的本构关系(3/5)
超弹性材料 假定材料具有单位质量的应变能函数，再根据能量原理来定义本构 假定材料具有单位质量的应变能函数， 单位质量的应变能函数 关系，这类材料称为超弹性材料。 关系，这类材料称为超弹性材料。
Kirchhoff应力： 应力： 应力
通过初时构型上的微元体定义的应力称为Kirchhoff应力，用 S 表示； 应力， 表示； 通过初时构型上的微元体定义的应力称为 应力 通过现时构型的微元体定义的应力称为现时 现时（ 应力， 通过现时构型的微元体定义的应力称为现时（Updated）Kirchhoff 应力， ） * 表示。 用 表示。 S
Case-1
W = W ( ε KL )
∂W ( ε KL ) ∂ε IJ
例如
W=
1 2ρ 0
2
ε IJ AIJKLε KL
(不限于这种形式） 不限于这种形式） 不限于这种形式 增量形式 …
现时Kirchhoff应力 应力 现时 或增量形式 …
S IJ = ρ 0
S IJ = ρ 0
一阶近似
∂ W ( ε MN ) ε KL ∂ε IJ ∂ε KL
∆ε IJ = ∂xm ∂xn * ∆ ε mn ∂X I ∂X J
现时（ 应变增量： 现时（Updated）Green应变增量： ） 应变增量
∆*ε ij = 1 ∂∆ui ∂∆u j 1 ∂∆uk ∂∆uk + + 2 ∂x j ∂xi 2 ∂xi ∂x j
= ∆*eij + ∆*ηij
2011-10-19 2
大变形问题的应变描述(1/4) 大变形问题的应变描述(1/4)
问题的特点：由于变形较大， 问题的特点：由于变形较大，使得不同时刻物体具有差别不能 忽略的不同构型，这是大变形问题分析的基本出发点。 忽略的不同构型，这是大变形问题分析的基本出发点。
xi
yi
XI
(a)
(b)
(c)
注意：我们用下标的大小写表示坐标的大小写，对应于不同的构型。 注意：我们用下标的大小写表示坐标的大小写，对应于不同的构型。 大变形分析由于采用增量方法，需经常用到它们的增量形式。 大变形分析由于采用增量方法，需经常用到它们的增量形式。
2011-10-19 4
大变形问题的应变描述(3/4) 大变形问题的应变描述(3/4)
∂yi ∂x j
D( N ) =
∂ ( x1 , x2 , x3 ) ∂xi = ∂ ( X 1 , X 2 , X 3 ) ∂X J
D*( N +1) =
Байду номын сангаас
∂ ( y1 , y2 , y3 ) ∂ ( x1 , x2 , x3 )
=
2011-10-19
8
大变形分析中的本构关系(1/5) 大变形分析中的本构关系(1/5)
应变增量： 应变增量： Green应变增量： 应变增量： 应变增量
∆ε IJ = 1 1 (δ KJ + uK , J ) ∆uK , I + (δ KI + uK , I ) ∆uK , J + ∆uK , I ∆uK , J 2 2 = ∆eIJ + ∆η IJ
线性部分
非线性部分
二者之间满足张 量变换关系！ 量变换关系！
∂σ ij ∂t = Aijkl ∂ε kl ∂t
（大变形分析中） 大变形分析中） 线弹性材料 (elasticity) 超弹性材料 (hyperelasticity) 次弹性材料 (hypoelasticity)
Aijkl
为常数
1 W = ε ij Aijkl ε kl 2
ν Aijkl = 2G δ ilδ jm + δ ijδ lm 1 − 2ν
2011-10-19 7
大变形问题的应力描述(2/2) 大变形问题的应力描述(2/2)
Kirchhoff、现时Kirchhoff及Euler应力（增量）间的关系： 、现时 应力（ 及 应力 增量）间的关系：
*Sij = σ ij + ∆ * Sij
现时Kirchhoff应力增量 应力增量 现时
现时Kirchhoff应力 应力 现时 t + ∆t 时刻
线性部分
非线性部分是高阶小量 对于小变形情形
∆ε IJ = ∆*ε ij = 1 ∂∆ui ∂∆u j + ≜ ∆ε ij ∂X i 2 ∂X j
现时（ 应变增量退化成： 现时（Updated）Green应变增量退化成： ） 应变增量退化成
∆*ε ij = 1 ∂∆ui ∂∆u j 1 ∂∆uk ∂∆uk + + 2 ∂x j ∂xi 2 ∂xi ∂x j
2011-10-19
线性部分
非线性部分
5
大变形问题的应变描述(4/4) 大变形问题的应变描述(4/4)
应变增量：（续）－对于大变形小应变情形 应变增量：（续）－对于大变形小应变情形 ：（ Green应变增量退化成： 应变增量退化成： 应变增量退化成
∆ε IJ = 1 1 (δ KJ + uK , J ) ∆uK , I + (δ KI + uK , I ) ∆uK , J + ∆uK , I ∆uK , J 2 2 = ∆eIJ + ∆η IJ
Case-1
ɺ S IJ = AIJK L εɺ K L
同乘以时间增量 ∆t
增量形式 …
Case-2
* * Sij J = Aijkl Dkl
可以证明， 可以证明，这两个率都与转动无关
Jaumann 应力率
* ɺ* ɺ* * ɺ * Sij J = Sij − Sik ωkj − S * ωki jk
ε KL =
1 ( uK ,L + uL, K + uM , K uM , L ) 2
现时（ 应变张量： 现时（Updated）Green应变张量：以现时构型为参考构 ） 应变张量 型所定义的应变， 型所定义的应变，数学表示为
ε kl =
1 ( uk ,l + ul ,k + um,k um,l ) 2
2011-10-19 9
大变形分析中的本构关系(2/5) 大变形分析中的本构关系(2/5)
弹性材料
应力与Green应变之间存在一一对应关系，则称这 应变之间存在一一对应关系， 若Kirchhoff应力与 应力与 应变之间存在一一对应关系 类材料为弹性材料 类材料为弹性材料
S IJ = F ( ε KL )
从当前构型中取出微元体，在其上定义的应力称为 应力， 从当前构型中取出微元体，在其上定义的应力称为Euler应力，用 σ 应力 表示。 应力代表物体的真实应力 表示。Euler应力代表物体的真实应力。然而，当前构型是待求的未知构 应力代表物体的真实应力。然而，当前构型是待求的未知构 因而，有必要通过已知构型上的微元体再对应力进行描述。 型，因而，有必要通过已知构型上的微元体再对应力进行描述。
= ∆*eij + ∆*ηij
2011-10-19
线性部分
目的：以大变形问题为例， 目的：以大变形问题为例，介绍几何非线性问题的有限元 方法。 方法。 特点：与线性有限元方法比较，几何关系不再是线性的。 特点：与线性有限元方法比较，几何关系不再是线性的。 内容： 内容： 引言 大变形问题的应变描述 大变形分析中的应力描述及本构关系 大变形问题有限元方程的建立 大变形分析中的载荷处理 小结
11
2011-10-19
现时构型时材料的密 随变形变化。 度－随变形变化。
大变形分析中的本构关系(4/5) 大变形分析中的本构关系(4/5)
次弹性材料 若应力率与变形率之间成线性变化规律，这类材料称为次弹性材料。但 应力率与变形率之间成线性变化规律，这类材料称为次弹性材料。 之间成线性变化规律 本构关系描述时要求“ 为与刚体转动无关的客观时间导数。 本构关系描述时要求“率”为与刚体转动无关的客观时间导数。
本构关系的客观性要求：需要选取合适的应力－ 本构关系的客观性要求：需要选取合适的应力－应变共轭对 描述材料的本构关系。 描述材料的本构关系。 弹性材料：加载曲线与卸载曲线相同的材料。 弹性材料：加载曲线与卸载曲线相同的材料。
，
本构关系有三种形式
σ ij = Aijkl ε kl
∂W σ ij = ∂ε ij
初始构型时材料 的密度－ 的密度－常数 Case-2
* W = W ( ε ij )
* ∂ ρ *W ( ε kl ) * Sij = * ∂ε ij
≜ AIJKLε KL
相 比 较
坐标变换
一阶近似
总之， 总之，对于一般的大变形 问题， 问题，在连续介质力学中 不能简化！ 不能简化！ 常用超弹性来表征材料的 本构关系。 本构关系。
初始构型（ 时刻 时刻） 初始构型（0时刻）
现时构型（ 时刻） 现时构型（t 时刻）
当前构型（ 时刻） 当前构型（ t + ∆t 时刻）
连续介质力学理论对物体经历大变形后的变形有严格的定义 连续介质力学理论对物体经历大变形后的变形有严格的定义 和推导。这里不准备过多引入复杂的概念和符号， 和推导。这里不准备过多引入复杂的概念和符号，而是与小变形 理论对照，介绍进行大变形分析时必需的几个概念和术语。 理论对照，介绍进行大变形分析时必需的几个概念和术语。
特殊情形
S IJ = AIJKLε KL
不依赖于构型变化 弹性本构关系多用于大位移（转动）小应变的情形。 弹性本构关系多用于大位移（转动）小应变的情形。 大位移 的情形
2011-10-19
10
大变形分析中的本构关系(3/5) 大变形分析中的本构关系(3/5)
超弹性材料 假定材料具有单位质量的应变能函数，再根据能量原理来定义本构 假定材料具有单位质量的应变能函数， 单位质量的应变能函数 关系，这类材料称为超弹性材料。 关系，这类材料称为超弹性材料。
Kirchhoff应力： 应力： 应力
通过初时构型上的微元体定义的应力称为Kirchhoff应力，用 S 表示； 应力， 表示； 通过初时构型上的微元体定义的应力称为 应力 通过现时构型的微元体定义的应力称为现时 现时（ 应力， 通过现时构型的微元体定义的应力称为现时（Updated）Kirchhoff 应力， ） * 表示。 用 表示。 S
Case-1
W = W ( ε KL )
∂W ( ε KL ) ∂ε IJ
例如
W=
1 2ρ 0
2
ε IJ AIJKLε KL
(不限于这种形式） 不限于这种形式） 不限于这种形式 增量形式 …
现时Kirchhoff应力 应力 现时 或增量形式 …
S IJ = ρ 0
S IJ = ρ 0
一阶近似
∂ W ( ε MN ) ε KL ∂ε IJ ∂ε KL
∆ε IJ = ∂xm ∂xn * ∆ ε mn ∂X I ∂X J
现时（ 应变增量： 现时（Updated）Green应变增量： ） 应变增量
∆*ε ij = 1 ∂∆ui ∂∆u j 1 ∂∆uk ∂∆uk + + 2 ∂x j ∂xi 2 ∂xi ∂x j
= ∆*eij + ∆*ηij
2011-10-19 2
大变形问题的应变描述(1/4) 大变形问题的应变描述(1/4)
问题的特点：由于变形较大， 问题的特点：由于变形较大，使得不同时刻物体具有差别不能 忽略的不同构型，这是大变形问题分析的基本出发点。 忽略的不同构型，这是大变形问题分析的基本出发点。
xi
yi
XI
(a)
(b)
(c)
注意：我们用下标的大小写表示坐标的大小写，对应于不同的构型。 注意：我们用下标的大小写表示坐标的大小写，对应于不同的构型。 大变形分析由于采用增量方法，需经常用到它们的增量形式。 大变形分析由于采用增量方法，需经常用到它们的增量形式。
2011-10-19 4
大变形问题的应变描述(3/4) 大变形问题的应变描述(3/4)
∂yi ∂x j
D( N ) =
∂ ( x1 , x2 , x3 ) ∂xi = ∂ ( X 1 , X 2 , X 3 ) ∂X J
D*( N +1) =
Байду номын сангаас
∂ ( y1 , y2 , y3 ) ∂ ( x1 , x2 , x3 )
=
2011-10-19
8
大变形分析中的本构关系(1/5) 大变形分析中的本构关系(1/5)
应变增量： 应变增量： Green应变增量： 应变增量： 应变增量
∆ε IJ = 1 1 (δ KJ + uK , J ) ∆uK , I + (δ KI + uK , I ) ∆uK , J + ∆uK , I ∆uK , J 2 2 = ∆eIJ + ∆η IJ
线性部分
非线性部分
二者之间满足张 量变换关系！ 量变换关系！
∂σ ij ∂t = Aijkl ∂ε kl ∂t
（大变形分析中） 大变形分析中） 线弹性材料 (elasticity) 超弹性材料 (hyperelasticity) 次弹性材料 (hypoelasticity)
Aijkl
为常数
1 W = ε ij Aijkl ε kl 2
ν Aijkl = 2G δ ilδ jm + δ ijδ lm 1 − 2ν
2011-10-19 7
大变形问题的应力描述(2/2) 大变形问题的应力描述(2/2)
Kirchhoff、现时Kirchhoff及Euler应力（增量）间的关系： 、现时 应力（ 及 应力 增量）间的关系：
*Sij = σ ij + ∆ * Sij
现时Kirchhoff应力增量 应力增量 现时
现时Kirchhoff应力 应力 现时 t + ∆t 时刻
线性部分
非线性部分是高阶小量 对于小变形情形
∆ε IJ = ∆*ε ij = 1 ∂∆ui ∂∆u j + ≜ ∆ε ij ∂X i 2 ∂X j
现时（ 应变增量退化成： 现时（Updated）Green应变增量退化成： ） 应变增量退化成
∆*ε ij = 1 ∂∆ui ∂∆u j 1 ∂∆uk ∂∆uk + + 2 ∂x j ∂xi 2 ∂xi ∂x j
2011-10-19
线性部分
非线性部分
5
大变形问题的应变描述(4/4) 大变形问题的应变描述(4/4)
应变增量：（续）－对于大变形小应变情形 应变增量：（续）－对于大变形小应变情形 ：（ Green应变增量退化成： 应变增量退化成： 应变增量退化成
∆ε IJ = 1 1 (δ KJ + uK , J ) ∆uK , I + (δ KI + uK , I ) ∆uK , J + ∆uK , I ∆uK , J 2 2 = ∆eIJ + ∆η IJ
Case-1
ɺ S IJ = AIJK L εɺ K L
同乘以时间增量 ∆t
增量形式 …
Case-2
* * Sij J = Aijkl Dkl
可以证明， 可以证明，这两个率都与转动无关
Jaumann 应力率
* ɺ* ɺ* * ɺ * Sij J = Sij − Sik ωkj − S * ωki jk
ε KL =
1 ( uK ,L + uL, K + uM , K uM , L ) 2
现时（ 应变张量： 现时（Updated）Green应变张量：以现时构型为参考构 ） 应变张量 型所定义的应变， 型所定义的应变，数学表示为
ε kl =
1 ( uk ,l + ul ,k + um,k um,l ) 2
2011-10-19 9
大变形分析中的本构关系(2/5) 大变形分析中的本构关系(2/5)
弹性材料
应力与Green应变之间存在一一对应关系，则称这 应变之间存在一一对应关系， 若Kirchhoff应力与 应力与 应变之间存在一一对应关系 类材料为弹性材料 类材料为弹性材料
S IJ = F ( ε KL )
从当前构型中取出微元体，在其上定义的应力称为 应力， 从当前构型中取出微元体，在其上定义的应力称为Euler应力，用 σ 应力 表示。 应力代表物体的真实应力 表示。Euler应力代表物体的真实应力。然而，当前构型是待求的未知构 应力代表物体的真实应力。然而，当前构型是待求的未知构 因而，有必要通过已知构型上的微元体再对应力进行描述。 型，因而，有必要通过已知构型上的微元体再对应力进行描述。
= ∆*eij + ∆*ηij
2011-10-19
线性部分