卡方检验

卡方检验的基本原理卡方检验是一种常用的统计方法，用于判断两个或多个分类变量之间是否存在显著性关联。

它基于卡方统计量的计算，通过比较实际观察值与理论预期值之间的差异来判断变量之间的关系。

本文将介绍卡方检验的基本原理及其应用。

一、卡方检验的基本原理卡方检验的基本原理是基于观察频数与期望频数之间的差异来判断变量之间的关联性。

在进行卡方检验之前，我们需要先了解以下几个概念：1. 观察频数（O）：指实际观察到的频数，即实际发生的次数。

2. 期望频数（E）：指在假设条件下，根据总体比例计算得到的预期频数。

3. 自由度（df）：指用于计算卡方统计量的自由变量的个数。

卡方统计量的计算公式如下：χ² = Σ((O-E)²/E)其中，Σ表示对所有分类进行求和。

卡方统计量的计算结果服从自由度为(df = (行数-1) * (列数-1))的卡方分布。

通过查表或计算卡方分布的p值，我们可以判断卡方统计量是否达到显著水平。

二、卡方检验的应用卡方检验可以应用于多种场景，以下是几个常见的应用示例：1. 拟合优度检验：用于判断观察频数与期望频数之间的差异是否显著。

例如，我们可以使用卡方检验来判断一组数据是否符合某个理论分布。

2. 独立性检验：用于判断两个分类变量之间是否存在关联。

例如，我们可以使用卡方检验来判断性别与喜好之间是否存在关联。

3. 分类变量的比较：用于比较两个或多个分类变量之间的差异。

例如，我们可以使用卡方检验来比较不同地区的人口分布是否存在差异。

4. 配对数据的比较：用于比较配对数据之间的差异。

例如，我们可以使用卡方检验来比较同一组人在不同时间点的健康状况是否存在差异。

三、卡方检验的限制虽然卡方检验是一种常用的统计方法，但也存在一些限制：1. 样本量要求：卡方检验对样本量的要求较高，特别是在分类变量较多或期望频数较低的情况下，需要保证样本量足够大。

2. 数据独立性：卡方检验要求观察数据之间相互独立，如果数据存在相关性或依赖性，可能会导致检验结果不准确。

卡方检验名词解释
卡方检验属于非参数检验，由于非参检验不存在具体参数和总体正态分布的假设，所以有时被称为自由分布检验。

参数和非参数检验最明显的区别是它们使用数据的类型。

非参检验通常将被试分类，如民主党和共和党，这些分类涉及名义量表或顺序量表，无法计算平均数和方差。

卡方检验分为拟合度的卡方检验和卡方独立性检验。

我们用几个例子来区分这两种卡方检验：
•对于可口可乐公司的两个领导品牌，大多数美国人喜欢哪一种？•公司采用了新的网页页面B，相较于旧版页面A，网民更喜欢哪一种页面？
以上两个例子属于拟合度的卡方检验，原因在于它们都是有关总体比例的问题。

我们只是将个体分类，并想知道每个类别中的总体比例。

它检验的内容仅涉及一个因素多项分类的计数资料，检验的是单一变量在多项分类中实际观察次数分布与某理论次数是否有显著差异。

拟合度的卡方检验定义：
主要使用样本数据检验总体分布形态或比例的假说。

测验决定所获得的的样本比例与虚无假设中的总体比例的拟合程度如何。

拟合度的卡方检验又叫最佳拟合度的卡方检验，为何取名“最佳拟合”？这是因为最佳拟合度的卡方检验的目的是比较数据（实际频数）与虚无假设。

确定数据如何拟合虚无假设指定的分布，因此取名“最佳拟合”。

关于拟合度的卡方检验有一些翻译上的区别，其实表达的是一个意思：
拟合度的卡方检验=卡方拟合优度检验=最佳拟合度卡方检验
以下统称：卡方拟合优度检验
卡方统计的公式：卡方卡方=χ2=Σ(fo−fe)2fe
公式中O代表observation，即实际频数；E代表Expectation，即期望频数。

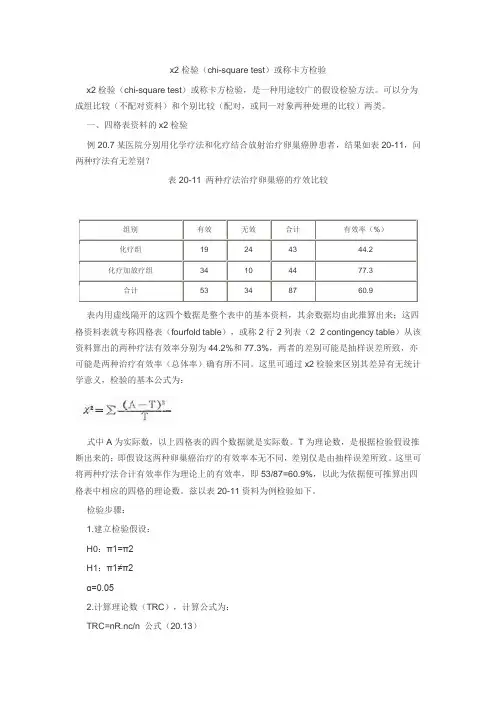
表内用虚线隔开的这四个数据是整个表中的基本资料，其余数据均由此推算出来；这四格资料表就专称四格表（fourfold table），或称2行2列表（2×2 contingency table）从该资料算出的两种疗法有效率分别为44.2%和77.3%，两者的差别可能是抽样误差所致，亦可能是两种治疗有效率（总体率）确有所不同。

这里可通过x2检验来区别其差异有无统计学意义，检验的基本公式为：式中A为实际数，以上四格表的四个数据就是实际数。

T为理论数，是根据检验假设推断出来的；即假设这两种卵巢癌治疗的有效率本无不同，差别仅是由抽样误差所致。

这里可将两种疗法合计有效率作为理论上的有效率，即53/87=60.9%，以此为依据便可推算出四格表中相应的四格的理论数。

兹以表20-11资料为例检验如下。

检验步骤：1.建立检验假设：H0：π1=π2H1：π1≠π2α=0.052.计算理论数（TRC），计算公式为：TRC=nR.nc/n 公式（20.13）因为上表每行和每列合计数都是固定的，所以只要用TRC式求得其中一项理论数（例如T1.1=26.2），则其余三项理论数都可用同行或同列合计数相减，直接求出，示范如下：T1.1=26.2T1.2=43-26.2=16.8T2.1=53-26.2=26.8T2.2=44-26.2=17.23.计算x2值按公式20.12代入4.查x2值表求P值在查表之前应知本题自由度。

按x2检验的自由度v=（行数-1）（列数-1），则该题的自由度v=（2-1）（2-1）=1，查x2界值表（附表20-1），找到x20.001（1）=6.63，而本题x2=10.01即x2＞x20.001（1），P＜0.01，差异有高度统计学意义，按α=0.05水准，拒绝H0，可以认为采用化疗加放疗治疗卵巢癌的疗效比单用化疗佳。

通过实例计算，读者对卡方的基本公式有如下理解：若各理论数与相应实际数相差越小，x2值越小；如两者相同，则x2值必为零，而x2永远为正值。

卡方检验的计算步骤
卡方检验是一种常用的统计学方法，用于检验两个或多个分类变量之间是否存在显著的关联性。

以下是卡方检验的计算步骤：
1.提出假设：根据研究问题，确定检验的假设，通常有两个假设：
-H0：两个分类变量之间不存在关联性；
-H1：两个分类变量之间存在关联性。

2.计算期望频数：根据样本数据，计算每个单元格（即每个交叉分类）的期望频数。

期望频数等于每个类别在样本中的频率乘以总样本量。

3.计算卡方值：根据期望频数和实际频数，计算卡方值。

卡方值的计算公式为：
其中，O表示实际频数，E表示期望频数。

4.确定自由度：卡方检验的自由度等于行数减去1乘以列数减去1。

5.查找临界值：根据自由度和显著性水平（通常为0.05或0.01），查找卡方分布表中的临界值。

6.作出决策：如果卡方值大于临界值，则拒绝H0，接受H1，认为两个分类变量之间存在关联性。

如果卡方值小于临界值，则不能拒绝H0，认为两个分类变量之间不存在关联性。

需要注意的是，在进行卡方检验时，需要注意样本量是否足够大，以及分类变量的类别是否存在不均衡的情况。

如果存在这些情况，可能会导致检验结果不准确。

卡方检验值的取值范围
卡方检验是一种统计方法，用于检查两个变量之间是否存在相关性。

具体来说，它比较实际观测值和预期值之间的偏差，并计算满足该偏差的概率。

卡方检验值的取值范围是由自由度决定的。

自由度指被研究数据中自由变异的数量。

在卡方检验中，自由度通常由两个变量的水平数目决定。

例如，对于一个2x2的列联表，自由度为1，因为只有一个方向上可以自由变化。

对于更大的表格，自由度的计算方法为自由变化的行数和列数之积。

卡方检验值的取值范围由自由度确定。

通常，在设定一个显著水平（例如0.05）的基础上，可以查表找到给定自由度下的临界值。

如果计算出的卡方值大于这个临界值，则认为在该显著水平下存在显著的相关性。

举例来说，一个2x2的列联表的卡方值可能在0到10之间取值，而自由度为1。

如果显著水平为0.05，则临界值为3.84。

如果计算出的卡方值大于3.84，则可以认为在这个显著水平下存在相关性。

如果计算出的卡方值小于3.84，则不能否定原假设，即认为两个变量之间不存在相关性。

总之，卡方检验值的取值范围是由自由度决定的，并且通常需要根据显著水平查表来判断是否存在相关性。

在应用卡方检验时应注意自由度的计算以及显著水平的设定。

卡方检验的参数
卡方检验是一种用于统计数据分析的方法，它用来判断两个分类变量之间是否存在相关性。

它基于观察到的数据与期望的数据之间的差异来进行推断。

卡方检验的参数包括样本数量、自由度和显著性水平。

样本数量是指参与检验的样本数量，它决定了卡方检验的可靠性。

自由度是指检验中独立的变量的数量，它与样本数量和分类变量的数量有关。

显著性水平是指在实际观察到的差异下，拒绝原假设的概率。

通常，我们使用显著性水平为0.05或0.01来进行判断。

在进行卡方检验时，我们首先需要建立原假设和备择假设。

原假设是指两个变量之间没有相关性，备择假设是指两个变量之间存在相关性。

然后，我们计算卡方值，并通过查阅卡方分布表来确定显著性水平下的临界值。

最后，比较计算得到的卡方值和临界值，如果计算得到的卡方值大于临界值，则拒绝原假设，认为两个变量之间存在相关性。

卡方检验可以应用于各种领域，例如医学、社会科学、市场调研等。

在医学领域，可以使用卡方检验来研究某种疾病与某种基因型之间的关系；在社会科学领域，可以使用卡方检验来研究教育水平与收入水平之间的关系；在市场调研领域，可以使用卡方检验来研究产品类型与购买决策之间的关系。

卡方检验是一种常用的统计方法，用于判断两个分类变量之间是否存在相关性。

它的参数包括样本数量、自由度和显著性水平。

通过计算卡方值并比较临界值，我们可以得出结论并进行进一步的数据分析。

卡方检验的原理卡方检验是一种用于检验两个分类变量之间是否存在相关性的统计方法。

它的原理是通过比较实际观察值和期望理论值之间的差异来判断两个变量之间的相关性程度。

在进行卡方检验时，我们首先需要构建一个列联表，然后根据列联表中的数据计算出卡方值，最后根据卡方值来判断两个变量之间的相关性程度。

首先，我们来看一下列联表的构建。

列联表是由两个分类变量的交叉分类频数构成的二维表格。

表格的行表示一个分类变量的各个分类，表格的列表示另一个分类变量的各个分类，交叉点上的数字表示对应分类组合的频数。

构建列联表的目的是为了清晰地展现两个变量之间的关系，为后续的卡方检验提供数据基础。

接下来，我们需要计算卡方值。

卡方值的计算公式为，χ²=Σ((O-E)²/E)，其中，Σ表示求和，O表示观察频数，E表示期望频数。

在计算卡方值时，我们需要先计算出期望频数，然后将观察频数和期望频数的差异进行平方，并除以期望频数，最后将所有分类组合的差异平方和除以期望频数的总和就得到了卡方值。

最后，我们根据卡方值来判断两个变量之间的相关性程度。

在进行判断时，我们需要参考自由度和显著性水平。

自由度的计算公式为，df=(r-1)(c-1)，其中，r表示行数，c表示列数。

在一般情况下，我们可以查找卡方分布表来确定显著性水平下的临界值，然后比较计算出的卡方值和临界值的大小关系，从而判断两个变量之间的相关性程度。

总的来说，卡方检验是一种用于检验两个分类变量之间相关性的统计方法，它通过比较实际观察值和期望理论值之间的差异来判断两个变量之间的相关性程度。

在进行卡方检验时，我们需要构建列联表，计算卡方值，并根据卡方值来判断两个变量之间的相关性程度。

通过卡方检验，我们可以更加清晰地了解两个变量之间的关系，为进一步的分析和决策提供依据。

方差分析与卡方检验方差分析（Analysis of Variance），简称ANOVA，是一种用于比较两个或多个组之间差异的统计方法。

它通过比较组内变异与组间变异的大小来判断不同组之间是否存在显著差异。

卡方检验（Chi-Square Test），又称χ²检验，是一种用于检验实际观测值与理论预期值之间是否存在显著差异的统计方法。

方差分析和卡方检验是常用的两种统计分析方法，本文将分别对它们进行介绍和比较。

一、方差分析方差分析是一种基于方差的统计方法，用于比较两个或多个样本均值之间的差异。

它适用于多个独立样本或多个相关样本之间的比较。

具体的步骤如下：1. 假设检验方差分析的假设检验通常基于以下假设：- 零假设（H0）：各组样本的均值相等。

- 备择假设（H1）：至少有一个组样本的均值与其他组不同。

2. 计算统计量方差分析中常用的统计量是F值。

F值是组间均方与组内均方之比，其具体计算公式为：F = 组间均方 / 组内均方3. 比较临界值根据给定的显著性水平（通常为0.05），查表或计算得到临界值。

4. 做出判断如果计算得到的F值大于临界值，则拒绝零假设，认为各组样本的均值存在显著差异；否则，接受零假设，认为各组样本的均值相等。

二、卡方检验卡方检验是一种用于检验实际观测值与理论预期值之间差异的统计方法。

它适用于分类变量之间的比较。

具体的步骤如下：1. 假设检验卡方检验的假设检验通常基于以下假设：- 零假设（H0）：实际观测值与理论预期值之间无显著差异。

- 备择假设（H1）：实际观测值与理论预期值之间存在显著差异。

2. 构建列联表根据实际观测值，构建列联表。

列联表是由多个分类变量组成的二维表格，用于统计不同组别之间的频数或频率。

3. 计算卡方值根据列联表中的实际观测频数和理论预期频数，计算卡方值。

卡方值的计算公式为：χ² = ∑ [(观测频数 - 预期频数)^2 / 预期频数]4. 比较临界值根据给定的自由度和显著性水平，查表或计算得到临界值。

卡方检验知识点总结卡方检验的原理是基于观测值与期望值的差异来进行判断的。

在卡方检验中，我们会对观测频数和期望频数进行比较，从而得出相关性的结论。

下面将详细介绍卡方检验的相关知识点。

1. 卡方检验的基本思想卡方检验的基本思想是比较观测频数与期望频数之间的差异，通过检验这种差异是否显著来判断两个变量之间的关系是否存在。

当观测频数与期望频数之间的差异较大时，可以认为两个变量之间存在相关性；当观测频数与期望频数之间的差异较小时，可以认为两个变量之间不存在相关性。

2. 卡方检验的适用条件在进行卡方检验时，需要满足一定的条件才能得到可靠的结果。

首先，变量的测量水平必须是分类（或者说是定性的）。

其次，样本的观测数据必须是频数形式，而且样本量要足够大（通常要求每个单元的期望频数不小于5）。

最后，在进行卡方检验前，需要明确变量之间的关系是独立的还是相关的。

3. 卡方检验的类型卡方检验有两种类型：独立性检验和拟合优度检验。

独立性检验是用于判断两个分类变量之间是否存在相关性，可以用于解决“两个变量关系是否显著”这类问题；拟合优度检验是用于判断观测频数与期望频数之间是否存在差异，可以用于解决“观测数据是否符合某种理论模型”这类问题。

4. 卡方检验的步骤进行卡方检验时，首先要确定研究的问题类型（是独立性检验还是拟合优度检验），然后计算卡方值，最后根据卡方值进行显著性检验。

具体的步骤如下：- 确定问题类型：根据研究的问题类型选择相应的卡方检验类型，是独立性检验还是拟合优度检验。

- 构建假设：根据问题类型构建原假设和备择假设，通常原假设是变量之间不存在相关性，备择假设是变量之间存在相关性。

- 计算卡方值：根据观测频数和期望频数计算卡方值，通常使用下面的公式进行计算：卡方值= Σ((观测频数-期望频数)² / 期望频数)。

- 计算自由度：根据研究问题的条件计算卡方检验的自由度，一般计算公式为：自由度 = (行数-1) * (列数-1)。

卡方检验又叫x 检验，通常用来对率(总体率或样本率)进行检验。

下面介绍下两样本率的卡方检验在对样本率进行卡方检验时，常采用表格方式进行处理，这种表格称为R×C联表，R和C分别代表表格的行和列数。

举个例子。

为了检验新的教学方法是否对提高学生的体质健康有校，选取一个实验班（50人）和一个对照班（53人），实验班采取新的教学方法，对照班采取原来的教学方法，经过一个学期后以下为SPSS的卡方检验操作步骤：1. 首先在SPSS里输入数据，注意数据输入的变量设置(“是否及格”设置为数值型，并且在label里设置1为及格，2为不及格）2. 对频数进行加权处理由于在SPSS里我们输入的不是原始数据，而是汇总数据，所以需要先进行加权处理。

执行“数据—>观测量加权”（data--weight cases），弹出对话框，对什么变量进行加权，选择“人数”3. 交叉分析同时进行卡方检验。

执行“分析—>描述统计—>交叉表”（analyze—>descriptive sta—>crosstabs），弹出对话框，行（row）选择变量“班级”，列（col）选择变量“是否及格”。

再点下面的“统计”按钮，弹出对话框，见下图，选中“卡方”（chi-square），然后点“继续”，返回到交叉表对话框。

我们输入的是实际频数，卡方检验还有一个很重要的变量就是“理论频数”，这里我们也要把“理论频数”也显示出来，点下面的“单元格（cells ）按钮，弹出对话框，在“计数”里选择“观察值”和“期望值”，见下图，然后点“继续”。

4. 查看结果。

最后点“确定”，就可得到检验结果。

见下面的图。

结果分析：1. 最上面的表格是对人数加权后得到的表格。

上面一排是实际计数值（实际频数），下面一排是理论计数值（理论频数）2. 下面的表格是卡方检验得到的结果。

Value是卡方值，df为自由度，sig为检验的P值。

我们看到上面有4种卡方检验的结果。

2χ检验概述 卡方检验是一种用途很广的计数资料的假设检验方法。

它属于非参数检验的范畴，主要是比较两个及两个以上样本率( 构成比）以及两个分类变量的关联性分析。

其根本思想就是在于比较理论频数和实际频数的吻合程度或拟合优度问题。

卡方检验是以卡方分布为基础的一种常用假设检验方法，主要用于分类变量，它的基本的无效假设是：H0：行分类变量与列分类变量无关联H1：行分类变量与列分类变量有关联α=0.05 统计量 ，其中Ai 是样本资料的计数，Ti 是在H0为真的情况下的理论数(期望值)。

在H0为真时，实际观察数与理论数之差Ai －Ti 应该比较接近0。

所以在H0为真时，检验统计量 服从自由度为k-1的卡方分布。

即： ，拒绝H0。

上述卡方检验由此派生了不同应用背景的各种问题的检验，特别最常用的是两个样本率的检验等。

计算方法及使用条件 卡方在分类资料统计推断中的应用，包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。

1、四格表资料的卡方检验四格表资料的卡方检验用于进行两个率或两个构成比的比较。

1）专用公式：若四格表资料四个格子的频数分别为a ，b ，c ，d ，则四格表资料卡方检验的卡方值=(ad − bc )2 * n /(a+b)(c+d)(a+c)(b+d)，自由度v=(行数-1)(列数-1)2)应用条件：221()ki i P i i A T T χ=-=∑221()k i i P i i A T T χ=-=∑22,P v αχχ>要求样本含量应大于40且每个格子中的理论频数不应小于5。

当样本含量大于40但理论频数有小于5的情况时卡方值需要校正，当样本含量小于40时只能用确切概率法计算概率。

2、行X列表资料的卡方检验行X列表资料的卡方检验用于多个率或多个构成比的比较。

1）专用公式：r行c列表资料卡方检验的卡方值=2)应用条件：要求每个格子中的理论频数T均大于5或1<T<5的格子数不超过总格子数的1/5。

卡方检验的应用条件和原理什么是卡方检验？卡方检验是一种用于比较两个或多个分类变量间是否存在显著差异的统计方法。

它基于观察值与期望值之间的差异，通过计算卡方值和查表得出结果。

卡方检验广泛应用于医学、社会科学、市场调查等领域。

卡方检验的原理卡方检验的原理基于卡方统计量的计算。

卡方统计量（χ²）是一种非负值，其计算公式如下：$\\chi^{2} = \\Sigma \\frac{(O_{ij} - E_{ij})^{2}}{E_{ij}}$其中，O ij是观察频数，表示实际观察到的某个组合的次数；E ij是期望频数，表示在假设成立的情况下，某个组合的理论次数。

卡方检验的原理是假设原始数据服从某种特定的分布（通常是期望频数分布），然后通过计算卡方统计量来检验观察频数与期望频数之间的差异。

如果差异显著，则可以拒绝原假设，认为变量之间存在显著性差异。

卡方检验的应用条件卡方检验的应用条件包括以下几个方面：1. 变量的类型卡方检验适用于两个或多个分类变量之间的比较。

分类变量是指被观察对象可以被分为有限个互斥的组别，例如性别（男、女）、教育程度（小学、初中、高中、大学）等。

2. 样本数量卡方检验要求样本数量足够大，以满足检验的统计功效。

一般来说，每个组别的期望频数不应小于5，否则卡方检验的结果可能不可靠。

3. 数据的独立性卡方检验假设观察数据是独立的，即不受其他因素的影响。

如果数据存在相关性或者重复观察现象，卡方检验结果可能会失真。

4. 原假设的满足卡方检验依赖于对原假设的明确表述。

原假设是关于样本或总体分布的猜想，一般是指变量之间不存在显著差异。

如果原假设无法明确表述或者不满足，卡方检验的结果可能无法得出有效结论。

如何进行卡方检验？进行卡方检验的主要步骤如下：1.确定原假设和备择假设：根据研究问题和数据特点，明确要检验的变量和假设。

2.计算观察频数和期望频数：根据实际观察数据和原假设，计算出各个组别的观察频数和期望频数。

卡方检验的适用范围与局限性卡方检验是一种常用的统计方法，用于确定两个或多个分类变量之间是否存在相关性。

它的适用范围广泛，但同时也存在一些局限性。

本文将讨论卡方检验的适用范围及其局限性，并探讨如何正确使用和解释卡方检验的结果。

一、卡方检验的适用范围1. 分类变量卡方检验适用于两种或更多种分类变量之间的相关性分析。

分类变量是指变量的取值是有限的，并且可以按照某种标准进行分组。

例如，性别（男、女）、教育程度（小学、初中、高中、大学）等都是分类变量。

2. 随机样本卡方检验要求数据是从一个随机样本中得出的。

这意味着样本应该是从总体中独立地选取的，并且每个观察值之间是相互独立的。

如果数据不满足这个条件，卡方检验的结果可能是不准确的。

3. 频数或比例卡方检验适用于具有频次或比例数据的情况。

频数是指每个分类中观察到的样本数，比例是指每个分类中观察到的比例或百分比。

例如，可以使用卡方检验来比较两个城市的人口分布情况，其中每个分类表示不同的年龄段。

二、卡方检验的局限性1. 样本量卡方检验对样本量的要求比较高。

如果样本量太小，检验结果可能不可靠。

通常来说，每个分类的期望频数应该大于5，以确保检验的精确性。

否则，可以使用精确的卡方检验方法来处理。

2. 假设的前提条件卡方检验基于一些假设的前提条件，如果这些前提条件不满足，卡方检验的结果可能不可靠。

这些前提条件包括独立性假设和期望频数假设。

独立性假设要求各个分类之间是相互独立的，期望频数假设要求每个分类的期望频数是已知的。

如果这些假设条件不满足，可以考虑使用其他的统计方法。

3. 多重比较问题当需要比较多个分类变量之间的差异时，卡方检验的结果可能产生多重比较问题。

这意味着检验结果可能会出现偶然性差异被错误地认为是真实差异的情况。

为了解决这个问题，可以使用多重校正方法，如Bonferroni校正或Benjamini-Hochberg校正。

三、正确使用和解释卡方检验的结果在进行卡方检验时，应确保数据满足检验的前提条件，并选择适当的检验方法。

卡方检验是一种用于比较两组或多组数据之间差异的统计方法，它基于卡方统计量，用于检测实际观测值与理论模型之间的差异。

卡方检验通常应用于以下条件：1. 观察值具有独立性和同分布性，即观察值之间没有相互影响，并且具有相同的分布。

这是进行卡方检验的基本前提，因为卡方检验是基于概率和频率的统计方法，如果观察值不满足独立性和同分布性，卡方检验的结果可能会受到干扰。

2. 观察值数量足够大，可以保证卡方检验的准确性和可靠性。

如果观察值数量过小，卡方检验的结果可能会受到偶然误差的影响，从而导致误判。

3. 观察值符合一定的频率分布，即观察值应该均匀地分布在一定的频数范围内。

如果观察值不符合一定的频率分布，卡方检验的结果可能会受到干扰。

在实际应用中，卡方检验通常适用于以下情况：1. 比较两组或多组数据的分类变量之间的差异。

例如，比较不同性别、年龄、职业等人群在某些特征上的分布是否存在差异。

2. 分析定性变量的相关关系。

虽然卡方检验主要用于比较两组数据的差异，但它也可以用于分析定性变量之间的相关关系。

通过卡方检验，可以确定变量之间的相关程度和可能的原因。

3. 检测分类变量之间是否存在逻辑关系。

例如，通过卡方检验可以检测某个分类变量是否与另一个分类变量存在一定的关联关系，如性别与婚姻状况的关系等。

需要注意的是，卡方检验是一种假设检验方法，需要设定一定的显著性水平来决定是否拒绝零假设。

通常，显著性水平越低，说明对零假设的拒绝越果断。

但在实际应用中，需要注意过低的显著性水平可能会导致过度判断错误的风险。

因此，在进行卡方检验时，需要根据具体情况选择合适的显著性水平，并谨慎评估检验结果的可信度。

同时，对于一些特殊情况，如样本量较小、数据分布不均匀等，可能需要采用其他统计方法或进行适当的调整来保证卡方检验的准确性和可靠性。

卡方检验的假设与局限性卡方检验是一种常用的统计方法，用于评估观察结果与理论模型之间的偏离程度。

在进行卡方检验时，需要根据具体的研究问题提出假设，并对其进行检验。

本文将探讨卡方检验的假设设定及其局限性。

一、卡方检验的假设设定卡方检验的假设设定包括零假设（H0）和备择假设（H1）。

零假设指的是没有任何关联或差异存在，即观察结果与理论模型完全一致。

备择假设则认为观察结果与理论模型存在关联或差异。

在卡方检验中，常见的假设设定包括：1. 假设设定一：分类变量之间不存在关联或差异。

在某些情况下，我们希望检验两个分类变量之间是否存在关联或差异。

例如，在某个人群中，我们想要了解性别与吸烟习惯之间是否存在关联。

零假设可以设定为“性别与吸烟习惯之间不存在关联”。

2. 假设设定二：观察频数与理论频数之间不存在差异。

在某些情况下，我们想要检验观察到的频数是否与根据理论模型预期的频数有所差异。

例如，在一次投票中，我们想要检验实际投票结果与预期投票比例是否存在差异。

零假设可以设定为“实际投票结果与预期投票比例完全一致”。

3. 假设设定三：样本来自同一总体。

在某些情况下，我们需要检验两个或多个样本是否来自同一总体。

例如，在药物治疗疾病的研究中，我们希望比较不同药物对疾病治疗效果的差异。

零假设可以设定为“不同药物对疾病治疗效果没有差异”。

二、卡方检验的局限性尽管卡方检验在很多实际问题中应用广泛，但也存在一些局限性。

1. 样本容量要求较高。

卡方检验的结果受样本容量的影响较大。

当样本容量较小时，卡方检验的统计功效较低，可能会导致无法检测到真实的关联或差异。

2. 对数据的要求较高。

卡方检验要求数据满足一些假设，例如每个观测值之间是独立的，期望频数应大于5等。

如果数据不满足这些要求，卡方检验的结果可能不可靠。

3. 不能确定关联或差异的原因。

卡方检验只能告诉我们观察结果与理论模型之间是否存在关联或差异，但无法确定具体的原因。

因此，在进行卡方检验时，需要结合实际背景和领域知识进行综合分析。