实验四 区域填充算法的实现

c语言多边形区域填充算法C语言多边形区域填充算法一、介绍多边形区域填充算法是计算机图形学中的一项重要技术，用于将给定的多边形区域进行填充，使其呈现出丰富的颜色或纹理，增强图形的效果和表现力。

本文将介绍一种常用的C语言多边形区域填充算法——扫描线填充算法。

二、扫描线填充算法原理扫描线填充算法是一种基于扫描线的填充方法，其基本思想是将多边形区域按照水平扫描线的顺序，从上到下逐行扫描，通过判断扫描线与多边形边界的交点个数来确定是否进入多边形区域。

具体步骤如下：1. 首先，确定多边形的边界，将其存储为一个边表。

边表中的每个边都包含起点和终点的坐标。

2. 创建一个活性边表（AET），用于存储当前扫描线与多边形边界的交点。

初始时，AET为空。

3. 从上到下逐行扫描多边形区域，对每一条扫描线，从边表中找出与该扫描线相交的边，并将其加入AET中。

4. 对于AET中的每一对交点，按照从左到右的顺序两两配对，形成水平线段，将其填充为指定的颜色或纹理。

5. 在扫描线的下一行，更新AET中的交点的坐标，然后重复步骤4，直到扫描到多边形区域的底部。

三、代码实现下面是一个简单的C语言实现扫描线填充算法的示例代码：```#include <stdio.h>#include <stdlib.h>#include <stdbool.h>typedef struct {int x;int y;} Point;typedef struct {int yMax;float x;float dx;int next;} Edge;void fillPolygon(int n, Point* points, int color) {// 获取多边形的边界int yMin = points[0].y;int yMax = points[0].y;for (int i = 1; i < n; i++) {if (points[i].y < yMin) {yMin = points[i].y;}if (points[i].y > yMax) {yMax = points[i].y;}}// 创建边表Edge* edges = (Edge*)malloc(sizeof(Edge) * n);int k = n - 1;for (int i = 0; i < n; i++) {if (points[i].y < points[k].y) {edges[i].yMax = points[k].y;edges[i].x = points[i].x;edges[i].dx = (float)(points[k].x - points[i].x) / (points[k].y - points[i].y);edges[i].next = k;} else {edges[i].yMax = points[i].y;edges[i].x = points[k].x;edges[i].dx = (float)(points[i].x - points[k].x) / (points[i].y - points[k].y);edges[i].next = i;}k = i;}// 扫描线填充for (int y = yMin; y < yMax; y++) {int xMin = INT_MAX;int xMax = INT_MIN;for (int i = 0; i < n; i++) {if (y >= edges[i].yMax) {continue;}edges[i].x += edges[i].dx;if (edges[i].x < xMin) {xMin = edges[i].x;}if (edges[i].x > xMax) {xMax = edges[i].x;}int j = edges[i].next;while (j != i) {edges[j].x += edges[j].dx; if (edges[j].x < xMin) {xMin = edges[j].x;}if (edges[j].x > xMax) {xMax = edges[j].x;}j = edges[j].next;}}for (int x = xMin; x < xMax; x++) { drawPixel(x, y, color);}}free(edges);}int main() {// 定义多边形的顶点坐标Point points[] = {{100, 100},{200, 200},{300, 150},{250, 100}};// 填充多边形区域为红色fillPolygon(4, points, RED);return 0;}```四、总结通过扫描线填充算法，我们可以实现对多边形区域的填充，从而提升图形的表现效果。

区域填充算法⼀、区域填充概念区域：指已经表⽰成点阵形式的填充图形，是象素的集合。

区域填充：将区域内的⼀点（常称种⼦点）赋予给定颜⾊，然后将这种颜⾊扩展到整个区域内的过程。

区域填充算法要求区域是连通的，因为只有在连通区域中，才可能将种⼦点的颜⾊扩展到区域内的其它点。

1、区域有两种表⽰形式1. 内点表⽰：枚举出区域内部的所有象素内部所有象素着同⼀个颜⾊边界像素着与内部象素不同的颜⾊。

2. 边界表⽰：枚举出区域外部的所有象素边界上的所有象素着同⼀个颜⾊内部像素着与边界象素不同的颜⾊。

2、区域连通1. 四向连通区域：从区域上⼀点出发可通过上、下、左、右四个⽅向移动的组合，在不越出区域的前提下，到达区域内的任意象素。

2. ⼋向连通区域：从区域上⼀点出发可通过上、下、左、右、左上、右上、左下、右下⼋个⽅向移动的组合，在不越出区域的前提下，到达区域内的任意象素。

3. 四连通与⼋连通区域的区别连通性：四连通可以看作⼋连通的⾃⼰，但是对边界有要求⼆、简单种⼦填充算法1、基本思想给定区域G⼀种⼦点（x, y）,⾸先判断该点是否是区域内的⼀点，如果是，则将该点填充为新的颜⾊，然后将该点周围的四个点（四连通）或⼋个点（⼋连通）作为新的种⼦点进⾏同样的处理，通过这种扩散完成对整个区域的填充。

这⾥给出⼀个四连通的种⼦填充算法（区域填充递归算法），使⽤【栈结构】来实现原理算法原理如下：种⼦像素⼊栈，当【栈⾮空】时重复如下三步：2、算法代码这⾥给出⼋连通的种⼦填充算法的代码：void flood_fill_8(int[] pixels, int x, int y, int old_color, int new_color) { if (x < w && x > 0 && y < h && y > 0) {// 如果是旧的颜⾊⽽且还没有给他填充过if (pixels[y * w + x] == old_color) {// 填充为新的颜⾊pixels[y * w + x]== new_color);// 递归flood_fill_8(pixels, x, y + 1, old_color, new_color);flood_fill_8(pixels, x, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y, old_color, new_color);flood_fill_8(pixels, x + 1, y + 1, old_color, new_color);flood_fill_8(pixels, x + 1, y - 1, old_color, new_color);flood_fill_8(pixels, x - 1, y + 1, old_color, new_color);flood_fill_8(pixels, x - 1, y - 1, old_color, new_color);}}}3、OpenCV实现import cv2def seed_fill(img):ret, img = cv2.threshold(img, 128, 255, cv2.THRESH_BINARY_INV) label = 100stack_list = []h, w = img.shapefor i in range(1, h-1, 1):for j in range(1, w-1, 1):if (img[i][j] == 255):img[i][j] = labelstack_list.append((i, j))while len(stack_list) != 0:cur_i = stack_list[-1][0]cur_j = stack_list[-1][1]img[cur_i][cur_j] = labelstack_list.remove(stack_list[-1])# 四邻域，可改为⼋邻域if (img[cur_i-1][cur_j] == 255):stack_list.append((cur_i-1, cur_j))if (img[cur_i][cur_j-1] == 255):stack_list.append((cur_i, cur_j-1))if (img[cur_i+1][cur_j] == 255):stack_list.append((cur_i+1, cur_j))if (img[cur_i][cur_j+1] == 255):stack_list.append((cur_i, cur_j+1))cv2.imwrite('./result.jpg', img)cv2.imshow('img', img)cv2.waitKey()if __name__ == '__main__':img = cv2.imread('./test.jpeg', 0)seed_fill(img)4、简单种⼦填充算法的优点和缺点优点：1. 该算法也可以填充有孔区域缺点：1. 有些像素会多次⼊栈，降低算法效率，栈结构占空间2. 递归执⾏，算法简单，但效率不⾼，区域内每⼀像素都要进/出栈，费时费内存3. 改进算法，减少递归次数，提⾼效率三、扫描线种⼦填充算法⽬标：减少递归层次适⽤于边界表⽰的4连通区间1、基本思想在任意不间断区间中只取⼀个种⼦像素（不间断区间指在⼀条扫描线上⼀组相邻元素），填充当前扫描线上的该段区间；然后确定与这⼀区段相邻的上下两条扫描线上位于区域内的区段，并依次把它们保存起来，反复进⾏这个过程，直到所保存的各个区段都填充完毕。

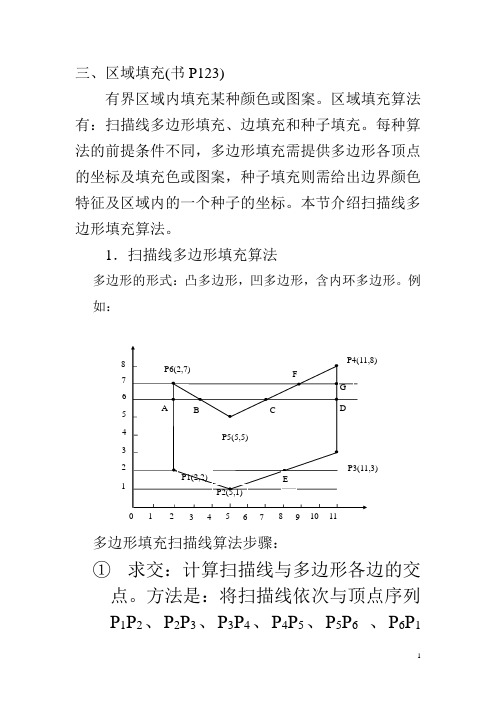
三、区域填充(书P123)有界区域内填充某种颜色或图案。

区域填充算法有：扫描线多边形填充、边填充和种子填充。

每种算法的前提条件不同，多边形填充需提供多边形各顶点的坐标及填充色或图案，种子填充则需给出边界颜色特征及区域内的一个种子的坐标。

本节介绍扫描线多边形填充算法。

1．扫描线多边形填充算法多边形的形式：凸多边形，凹多边形，含内环多边形。

例如：多边形填充扫描线算法步骤：① 求交：计算扫描线与多边形各边的交点。

方法是：将扫描线依次与顶点序列P 1P 2、P 2P 3、P 3P 4、P 4P 5、P 5P 6 、P 6P 111 2 233 4 455 6 677 8 8 9 10 11P2(5,1)EP3(11,3)DP4(11,8)GFCBP5(5,5)P6(2,7)AP1(2,2)相交。

例：扫描线6有四个交点。

②排序：把所有交点按x值升序排列。

③配对：1、2，3、4…交点两两相配。

即（1，2）、（3，4）、…。

④填色：把交点对之间的颜色置为指定颜色；交点对以外的象素置为背景色（或不变）。

求解时存在两个问题：问题一（取交点问题）：扫描线与多边形顶点相交时会出现异常情况。

如扫描线2与边P1P2和P1P6相交问题：若按前述方法求得交点的x坐标，序列为2,2,8，这将导致[2,8] 区间内的象素取背景色。

如取1个交点，序列成为2,8，这是我们所需要的结果。

但如按上述新规则，扫描线7与P6相交取1点，交点序列为2,9,11，这将导致错把[2,9] 区间作为多边形内部来填充，正确做法应该取0个（9,11）或2个（2,2,9,11）交点。

为此，归纳规定如下：检查顶点两条边的另外两个端点的y值，端点y值>扫描线y值的个数取顶点数是否在扫描线两侧Y 1 1N 2 2N 0 0所以P1处取1个交点，P2处取2个，P5处取2个，P6处取0个。

问题二（边界上象素的取舍问题）：如下图，左下角坐标(1,1) ，右上角坐标(3,3)，若对边界上所有象素均进行填充，则填充区域为3×3，但实际区域应为2×2。

试验实验一:图形的区域填充一、实验目的区域填充是指先将区域内的一点（常称为种子点）赋予给定颜色，然后将这种颜色扩展到整个区域内的过程。

区域填充技术广泛应用于交互式图形、动画和美术画的计算机辅助制作中。

本实验采用递归填充算法或打描线算法实现对光栅图形的区域填充。

通过本实验，可以掌握光栅图形编程的基本原理和方法。

实验内容掌握光栅图形的表示方法，实现种子算法或扫描线算法。

通过程序设计实现上述算法。

建议采用VC++实现OpenGL程序设计。

三、实验原理、方法和手段递归算法在要填充的区域内取一点（X, Y）的当前颜色记为oldcoloo用要填充的颜色ne wcolor去取代，递归函数如下：procedure flood-fill（XXoldcoloLnewcolor:integer）; beginif getpixel（fiainebufier,x,y）=oldcolorthen beginsetpixel（fiamebuffer,x,y,newcolor）; flood-fill（X.Y+1 .oldcoloLiiewcolor）;flood-fill（X.Y^ 1 ,oldcoloi;newcolor）; flood-fill（X-l,Y；oldcoloi;newcolor）; flood-fill（X+l,Yoldcoloi;newcolor）;endend扫描线算法扫描线算法的效率明显高于递归算法，其算法的基本思想如下：（1）（初始化）将算法设置的堆栈置为空，将给定的种子点（x,y）压入堆栈。

（2）（出栈）如果堆栈为空，算法结束；否则取栈顶元素（x,y）作为种子点。

（3）（区段填充）从种子点（x,y）开始沿纵坐标为y的当前扫描线向左右两个方向逐个象素进行填色，其值置为newcoloi;直到抵达边界为止。

（4）（定范围）以XleA和Xn血分别表示在步骤3中填充的区段两端点的横坐标。

（5）（进栈）分别在与当前扫描线相邻的上下两条打描线上，确定位于区间［Xldb Xn 曲］内的给定区域的区段。

计算机图形学-区域填充的扫描线算法计算机图形学——区域填充的扫描线算法一．实验名称：区域填充的扫描线算法二．实验目的：1、理解区域填充扫描线算法的原理；2、实现区域填充的扫描线算法并测试；三．算法原理：算法基本思想: 首先填充种子点所在扫描线上位于区域内的区段，然后确定与该区段相邻的上下两条扫描线上位于区域内的区段，并依次将各区段的起始位置保存, 这些区段分别被用区域边界色显示的像素点所包围。

随后,逐步取出一开始点并重复上述过程，直到所保存各区段都填充完毕为止。

借助于栈结构，区域填充的扫描线算法之步骤如下：Step 1. 初始化种子点栈：置种子点栈为空栈，并将给定的种子点入栈；Step 2. 出栈：若种子点栈为空，算法结束；否则，取栈顶元素(x，y)为种子点；Step 3. 区段填充：从种子点(x, y) 开始沿纵坐标为y 的当前扫描线向左右两个方向逐像素点进行填色，其颜色值置为newcolor 直至到达区域边界。

分别以xl 和xr 表示该填充区段两端点的横坐标；Step 4. 新种子点入栈: 分别确定当前扫描线上、下相邻的两条扫描线上位于区段[xl, xr] 内的区域内的区段。

若这些区段内的像素点颜色值为newolor ,则转至Step 2；否则以区段的右端点为种子点入种子点栈，再转至Step 2。

四．原程序代码：/*****************************************//*4-ScanLineFill 区域填充的扫描线算法实现*//*****************************************/#include#include#include#include#define Stack_Size 100 //栈的大小常量//定义结构体,记录种子点typedef struct{int x;int y;}Seed;//定义顺序栈(种子点)typedef struct{Seed Point[Stack_Size];int top;}SeqStack;//初始化栈操作void InitStack(SeqStack *&S){S=(SeqStack *)malloc(sizeof(SeqStack)); S->top=-1;}//种子点栈置空；void setstackempty (SeqStack *S){S->top==-1;}//种子点栈状态检测函数int isstackempty (SeqStack *S){if(S->top==-1)return true; //空栈返回trueelsereturn false; //非空栈返回false}//种子点入栈；int stackpush (SeqStack *&S,Seed point){if(S->top==Stack_Size-1)//栈已满，返回false return false; S->top++;//栈未满，栈顶元素加1S->Point[S->top]= point;return true;}//取栈顶元素；int stackpop (SeqStack *&S,Seed &point){if(S->top==-1)//栈为空，返回falsereturn false;point=S->Point[S->top];S->top --;//栈未空，top减1return true;}//画圆void CirclePoints (int xc, int yc, int x, int y, int Color) { putpixel (xc + x, yc + y, Color);putpixel (xc + x, yc - y, Color);putpixel (xc - x, yc + y, Color);putpixel (xc - x, yc - y, Color);putpixel (xc + y, yc + x, Color);putpixel (xc + y, yc - x, Color);putpixel (xc - y, yc + x, Color);putpixel (xc - y, yc - x, Color); }//中点画圆算法void MidpointCircle(int radius, int Color) {int x, y;float d;x=0;y=radius;d=5.0/4-radius;CirclePoints(250,250,x,y,Color);while(x<y)< p="">{if (d<0){d+=x*2.0+3;}else{d+=(x-y)*2.0+5;y--;}x++;CirclePoints(250,250,x,y,Color);}}//四连通扫描线算法void ScanLineFill4(int x, int y, int oldcolor, int newcolor) { int xl, xr, i;bool SpanNeedFill;Seed pt;//种子点SeqStack *S;//定义顺序栈InitStack(S);//定义了栈之后必须把栈先初始化setstackempty(S);//种子点栈置空；pt.x = x;pt.y = y;stackpush (S,pt); // 种子点(x, y)入栈while (!isstackempty(S)){stackpop (S,pt);//取种子点y = pt.y;x = pt.x;while (getpixel (x,y)==oldcolor) {// 从种子点开始向右填充putpixel (x, y, newcolor);x++;}xr = x -1;x = pt.x -1;while (getpixel (x,y)==oldcolor) { // 从种子点开始向左填充putpixel (x, y, newcolor);x--;}xl = x + 1;x = xl;y = y +1; // 处理上面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill = true;x++ ;} // 待填充区段搜索完毕if (SpanNeedFill){// 将右端点作为种子点入栈pt.x = x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill = false;} //继续向右检查以防遗漏while ((getpixel (x, y)!=oldcolor) && (x< xr)) x++; } //上一条扫描线上检查完毕x = xl;y=y-2; // 处理下面一条扫描线while (x < xr){SpanNeedFill = false;while (getpixel (x, y)==oldcolor){SpanNeedFill=true;x++ ;}if (SpanNeedFill){pt.x= x - 1;pt.y = y;stackpush (S,pt);SpanNeedFill=false;}while ((getpixel (x, y)!=oldcolor) && (x < xr))x++;}}}//主函数检测void main(){int radius,color;int x,y;//种子点int oldcolor,newcolor;//原色与填充色//输入参数值printf("input radius and color:\n");//画圆参数scanf("%d,%d",&radius,&color);printf("input x and y:\n"); //读入内点scanf("%d,%d", &x, &y);printf("input oldcolor and newcolor:\n"); //读入原色与填充色scanf("%d,%d", &oldcolor, &newcolor);int gdriver = DETECT,gmode;initgraph(&gdriver, &gmode, "c:\\tc");// 用背景色清空屏幕cleardevice();// 设置绘图色为红色setcolor(RED);MidpointCircle(radius,color);//用中点画圆算法画圆rectangle(150, 150, 350, 350);//再画一个矩形区域ScanLineFill4 (x,y,oldcolor,newcolor);//扫描线区域填充getch();closegraph();}五．运行结果与讨论：测试结果1：测试结果2：六．实验分析与讨论：1.通过借助栈这一数据结构，完成了区域填充的扫描线算法的实现，并利用以前所学的画圆等算法，进行综合运用，在此基础上进行扩充，设计多种图案，进行扫描线填充算法的检测，都得到了理想的结果，体现了算法的有效性；2.栈的数据结构给种子点的操作带来了极大的方便，为算法的实现提供了便利，同时还提高了算法的复用性和可靠性；3.此扫描线填充算法能够对多种图案进行填充，展现了算法的实用性。