高考聚焦小题——小卷强化训练六及参考答案

高考聚焦小题——小卷强化训练三十四班级 __________ 姓名 __________ 分数 __________ 一、 填空题：本大题共8小题，每题5分，共40分．1. 已知集合A ＝{2，3}，B ＝{1，log 2a }，若A ∩B ＝{3}，则实数a 的值为________．2. 古代科举制度始于隋而成于唐，完备于宋、元．明代则处于其发展的鼎盛阶段．其表现之一为会试分南卷、北卷、中卷，按比例录取，其录取比例为11∶7∶2.若明宣德五年会试录取人数为100，则中卷录取人数为________．(第3题)3. 从某校高三年级随机抽取一个班，对该班45名学生的高校招生体检表中视力情况进行统计，其结果的频率分布直方图．若某高校A 专业对视力要求不低于0.9，则该班学生中最多有________人能报考A 专业．4. 在正三棱锥ABCD 中，AB ⊥AC ，且BC ＝1，则三棱锥ABCD 的高为________．5. 如图，三个相同的正方形相接，则tan ∠ABC 的值为________．6. 若双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为3，其渐近线与圆x 2＋y 2－6y ＋m ＝0相切，则m 的值是________．7. 在△ABC 中，若AB →·AC →＝8，|AB →－2AC →|＝6，则△ABC 面积的最大值为________． 8. 已知函数f (x )＝错误!若f (x )＝a 有且只有一个根，则实数a 的取值范围是________． 二、 解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤．9. (本小题满分14分)如图，四边形ABCD 是菱形，DE ⊥平面ABCD ，AF ∥DE ，DE ＝2AF .求证： (1) AC ⊥平面BDE ； (2) AC ∥平面BEF .某公司生产的某批产品的销售量p 万件(生产量与销售量相等)与促销费用x 万元满足p ＝x ＋24(其中0≤x ≤a ，a 为正常数)．已知生产该产品还需投入成本6(p ＋1p)万元(不含促销费用)，产品的销售价格定为(4＋20p)元/件．(1) 将该产品的利润y 万元表示为促销费用x 万元的函数； (2) 促销费用投入多少万元时，该公司的利润最大？在平面直角坐标系xOy中，已知椭圆x2a2＋y2b2＝1(a>b>0)的焦距为2，离心率为22，椭圆的右顶点为A.(1) 求该椭圆的方程；(2) 过点D(2，－2)作直线PQ交椭圆于两个不同点P，Q，求证：直线AP，AQ 的斜率之和为定值．已知两个无穷数列{a n}和{b n}的前n项和分别为S n，T n，a1＝1，S2＝4，对任意的n∈N*，都有3S n＋1＝2S n＋S n＋2＋a n.(1) 求数列{a n}的通项公式；(2) 若{b n}为等差数列，对任意的n∈N*，都有S n＞T n，求证：a n＞b n；(3) 若{b n}为等比数列，b1＝a1，b2＝a2，求满足a n＋2T nb n＋2S n＝a k(k∈N*)的n的值．小卷强化训练三十四1. 8 解析：因为A ∩B ＝{3}，所以log 2a ＝3，即a ＝8.2. 10 解析：由题意，明宣德五年会试录取人数为100，则中卷录取人数为100×211＋7＋2＝10.3. 18 解析：某高校A 专业对视力要求不低于0.9，则该班能报考A 专业的学生数为45×(1＋0.75＋0.25)×0.2＝18.4. 66解析：设三棱锥ABCD 的高为h.依题意，得AB ，AC ，AD 两两垂直，且AB ＝AC ＝AD ＝22BC ＝22，△BCD 的面积为34×12＝34.由V ABCD ＝V BACD ，得13S △BCD ·h ＝13S △ACD ·AB ，即13×34×h ＝13×12×⎝⎛⎭⎫222×22，解得h ＝66，即三棱锥ABCD 的高h ＝66. 5. 17解析：设最右边的正方形的右下角顶点为D ，则 tan ∠ABC ＝tan (∠BCD －∠BAD)＝tan ∠BCD －tan ∠BAD 1＋tan ∠BCD tan ∠BAD ＝12－131＋12×13＝17.6. 8 解析：因为ca＝3，即c ＝3a ，b ＝9a 2－a 2＝22a ，所以该双曲线的渐近线方程为y ＝±22x.而圆的圆心为(0，3)，半径r ＝9－m ，由题设d ＝38＋1＝9－m ，即9－m ＝1，故m ＝8.7.152解析：在△ABC 中延长AC 到点D ，使AC ＝CD ，所以AD →＝2AC →.由已知可得AB →·AD →＝16，|AB →－AD →|＝6，以边BD 所在直线为x 轴，边BD 的中点为坐标原点建立平面直角坐标系，由|AB →－AD →|＝6，得|BD →|＝6，所以B(－3，0)，D(3，0)．设A(x ，y)，因为AB →·AD →＝16，所以x 2＋y 2＝25(y ≠0)，则0<|y|≤5，所以S △ABC ＝12×12|BD →||y|，所以0<S △ABC ≤152.故△ABC面积的最大值为152.8. (1，＋∞)解析：f(x)＝⎩⎪⎨⎪⎧|x －1|，x ∈（0，2]，|x －3|，x ∈（2，4]，|x －5|，x ∈（4，＋∞），作出f(x)的函数图象如图所示：由图象可知当a ＞1时，f(x)＝a 只有1个解．9. 证明：(1) 因为DE ⊥平面ABCD ，AC ⊂平面ABCD ，所以DE ⊥AC.(2分)因为四边形ABCD 是菱形，所以AC ⊥BD.(4分) 因为DE ∩BD ＝D ， 所以AC ⊥平面BDE.(7分)(2) 如图，设AC ∩BD ＝O ，取BE 中点G ，连结FG ，OG ，所以OG ∥12DE ，且OG ＝12DE.(10分)因为AF ∥DE ，DE ＝2AF ，所以AF ∥OG 且AF ＝OG ， 从而四边形AFGO 是平行四边形，FG ∥AO.(12分) 因为FG ⊂平面BEF ，AO ⊄平面BEF ， 所以AO ∥平面BEF ，即AC ∥平面BEF.(14分)10. 解：(1) 由题意知y ＝⎝⎛⎭⎫4＋20p p －x －6⎝⎛⎭⎫p ＋1p .(3分)将p ＝x ＋24代入化简，得y ＝19－24x ＋2－32x(0≤x ≤a)．(5分)(2) y ＝22－32⎝ ⎛⎭⎪⎫16x ＋2＋x ＋2≤22－316x ＋2×（x ＋2）＝10，当且仅当16x ＋2＝x ＋2，即x ＝2时，上式取等号．(8分)当a ≥2时，促销费用投入2万元时，该公司的利润最大．(9分)由y ＝19－24x ＋2－32x ，得y′＝24（x ＋2）2－32，当x<2时，y ′>0，此时函数y 在[0，2)上单调递增， 所以当a<2时，函数y 在[0，a)上单调递增，(11分)所以当x ＝a 时，函数有最大值，即促销费用投入a 万元时，该公司的利润最大．(12分)综上，当a ≥2时，促销费用投入2万元时，该公司的利润最大；当0≤a<2时，促销费用投入a 万元时，该公司的利润最大．(14分)11. (1) 解：由题知c ＝1，e ＝c a ＝22，所以a ＝2，b ＝1.(2分)所以椭圆的方程为x22＋y 2＝1.(4分)(2) 证明：当直线PQ 的斜率不存在时，不合题意；(5分)当直线PQ 的斜率存在时，设直线PQ 的方程为y ＋2＝k(x －2)， 代入x 2＋2y 2＝2，得(1＋2k 2)x 2－42(k 2＋k)x ＋4k 2＋8k ＋2＝0.(8分)由Δ＝－8(4k ＋1)>0，得k<－14.设P(x 1，y 1)，Q(x 2，y 2)，则x 1＋x 2＝42（k 2＋k ）1＋2k 2，x 1x 2＝4k 2＋8k ＋21＋2k 2.(10分)又k AP ＋k AQ ＝y 1x 1－2＋y 2x 2－2＝k （x 1－2）－2x 1－2＋k （x 2－2）－2x 2－2＝2k －2（x 1＋x 2）－4x 1x 2－2（x 1＋x 2）＋2＝2k －2×42（k 2＋k ）1＋2k 2－44k 2＋8k ＋21＋2k 2－2×42（k 2＋k ）1＋2k 2＋2＝1.所以直线AP ，AQ 的斜率之和为定值1.(16分)12. (1) 解：由3S n ＋1＝2S n ＋S n ＋2＋a n ，得2(S n ＋1－S n )＝S n ＋2－S n ＋1＋a n ，即2a n ＋1＝a n ＋2＋a n ，所以a n ＋2－a n ＋1＝a n ＋1－a n .(2分) 由a 1＝1，S 2＝4可知a 2＝3.所以数列{a n }是以1为首项，2为公差的等差数列． 故{a n }的通项公式为a n ＝2n －1.(4分)(2) 证明：设数列{b n }的公差为d ，则T n ＝nb 1＋n （n －1）2d ，由(1)知S n ＝n 2.因为S n >T n ，所以n 2>nb 1＋n （n －1）2d ，即(2－d)n ＋d －2b 1>0恒成立，所以⎩⎪⎨⎪⎧2－d ≥0，2－d ＋d －2b 1＞0，即⎩⎨⎧d ≤2，b 1<1.(6分)所以a n －b n ＝2n －1－b 1－(n －1)d ＝(2－d)n ＋d －1－b 1≥(2－d)＋d －1－b 1＝1－b 1>0. 所以a n >b n ，得证．(8分) (3) 解：由(1)知S n ＝n 2.因为{b n }为等比数列，且b 1＝1，b 2＝3， 所以{b n }是以1为首项，3为公比的等比数列．所以b n ＝3n －1，T n ＝3n－12.(10分)则a n ＋2T n b n ＋2S n ＝2n －1＋3n －13n －1＋2n 2＝3n ＋2n －23n －1＋2n 2＝3－6n 2－2n ＋23n －1＋2n 2. 因为n ∈N *，所以6n 2－2n ＋2>0，所以a n ＋2T n b n ＋2S n<3.(12分)而a k ＝2k －1，所以a n ＋2T nb n ＋2S n ＝1，即3n －1－n 2＋n －1＝0 (*)． 当n ＝1，2时，(*)式成立；(14分) 当n ≥2时，设f (n )＝3n －1－n 2＋n －1，则f (n ＋1)－f (n )＝3n －(n ＋1)2＋n －(3n －1－n 2＋n －1)＝2(3n －1－n )>0， 所以0＝f (2)<f (3)<…<f (n )<f (n ＋1)＜… 故满足条件的n 的值为1和2.(16分)。

小题天天练61．下列各句中加点成语的使用，全都不正确的一项是()①北方的冬天是漫长而寒冷的，但北国的冬天又总是那么富有韵味，银装素裹，囊萤映．．．雪．。

常常令生长在南方的游客流连忘返。

②面对捧场的观众，导演很感谢大家的支持，希望大家可以口耳相传．．．．，让越来越多的人可以去电影院支持他的电影。

③远远的，一片灯火辉煌，流光溢彩．．．．的宫殿映入眼帘，那便是闻名遐迩的哈尔滨“冰雪大世界”。

④中国杯首战，年轻的国足队员在上半场前半段的表现可圈可点．．．．，虽然没能将优势转化为进球，但场面仍然占优。

⑤有些地方不是保护自己独特的文化，更多的是拿来圈地设卡，建高档宾馆，设度假基地，这种做法无异于焚琴煮鹤．．．．，令人痛心。

⑥近日，由于楼市投机者东山再起．．．．，为给仍然躁动不安的楼市继续降温，上海、重庆同日发布新政，由此可知未来热点城市房地产市场持续收紧是大概率事件。

A．①②⑥B．①③⑤C．②③④D．④⑤⑥解析：本题考查正确使用成语(熟语)的能力。

①囊萤映雪：原是车胤用口袋装萤火虫来照书本，孙康利用雪的反光勤奋苦学的故事。

后形容刻苦攻读。

此处望文生义。

②口耳相传：口说耳听地往下传授。

此处对象语境不合。

③流光溢彩：流光：流动、闪烁的光彩；溢彩：色彩像要溢出来。

多用于形容车灯、霓虹等，有时候也用来形容时装表演和珠宝。

使用正确。

④可圈可点：指文章精彩，值得加以圈点，也引申为事物值得称赞。

使用正确。

⑤焚琴煮鹤：把琴当柴烧，把鹤煮了吃。

比喻糟蹋美好的事物。

使用正确。

⑥东山再起：失职后再度任职，或失败后恢复力量再干。

该成语多形容政治人物，而此处用错对象，错误用作投机者。

答案：A2．下列各句中，没有语病的一项是()A．我国是世界上除格陵兰和南极冰盖之外最重要的冰川集结地，每年提供700多亿立方米的淡水资源，是我国西北干旱地区的命脉，被誉为“生命之泉”。

B．户籍制度的改革牵动着无数人的心，因为它带来的将不仅是城市和农村称谓上的变革，更预示着变革背后人们的命运可能由之发生的改变。

高考聚焦小题——小卷强化训练九班级 __________ 姓名 __________ 分数 __________ 一、 填空题：本大题共8小题，每题5分，共40分．1. 已知向量a ＝(－1，2)，b ＝(m ，1)．若向量a ＋b 与a 垂直，则m ＝________．2. 如图，正方形ABCD 内的图形来自中国古代的太极图．正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称．在正方形内随机取一点，则此点取自黑色部分的概率是________．3. 如图，在△ABC 中，已知AN →＝12AC →，P 是BN 上一点．若AP →＝mAB →＋14AC →，则实数m 的值是________．(第2题)(第3题)(第4题)4. 如图，正方体ABCDA 1B 1C 1D 1的棱长为1，E ，F 分别为线段AA 1，B 1C 上的点，则三棱锥D 1DEF 的体积为________．5. 已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧2x －y ≥0，x ＋y －4≥0，x ≤3，则2x 3＋y3x 2y的取值范围是________．6. 若x ＝－2是函数f (x )＝(x 2＋ax －1)e x －1的极值点，则f (x )的极小值为________．7. 若数列⎩⎨⎧⎭⎬⎫2n （2n －1）（2n ＋1－1）的前k 项的和不小于2 0182 019，则k 的最小值为________．8. 在平面直角坐标系 xOy 中，A (－12，0)，B (0，6)，点P 在圆O ：x 2＋y 2＝50上．若PA →·PB →≤20，则点P 的横坐标的取值范围是________．二、 解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤．9. (本小题满分14分)在△ABC 中，a ，b ，c 分别为内角A ，B ，C 的对边，且b sin 2C ＝c sin B . (1) 求角C ；(2) 若sin(B －π3)＝35，求sin A 的值．在一张足够大的纸板上截取一个面积为3 600平方厘米的矩形纸板ABCD，然后在矩形纸板的四个角上切去边长相等的小正方形，再把它的边沿虚线折起，做成一个无盖的长方体纸盒(如图)．设小正方形边长为x厘米，矩形纸板的两边AB，BC的长分别为a厘米和b 厘米，其中a≥b.(1) 当a＝90时，求纸盒侧面积的最大值；(2) 试确定a，b，x的值，使得纸盒的体积最大，并求出最大值．已知斜率为k 的直线l 与椭圆C ：x 24＋y 23＝1交于A ，B 两点，线段AB 的中点为M (1，m )(m >0)．(1) 求证：k <－12；(2) 设F 为C 的右焦点，P 为C 上一点，且FP →＋FA →＋FB →＝0.求证：|FA →|，|FP →|，|FB →|成等差数列，并求该数列的公差．设等差数列{a n }是无穷数列，且各项均为互不相同的正整数． (1) 设数列{a n }的前n 项和为S n ，b n ＝S na n －1，n ∈N *.① 若a 2＝5，S 5＝40，求b 2的值； ② 若数列{b n }为等差数列，求b n .(2) 求证：数列{a n }中存在三项(按原来的顺序)成等比数列．小卷强化训练九参考答案1. 7 解析：由题意，得a ＋b ＝(m －1，3)．因为(a ＋b )·a ＝0，所以－(m －1)＋2×3＝0，解得m ＝7.2. π8解析：不妨设正方形边长为a.由图形的对称性可知，太极图中黑、白部分面积相等，即各占圆面积的一半．由几何概型概率的计算公式，得所求概率为12×π×⎝⎛⎭⎫a 22a 2＝π8.3. 12 解析：∵ B ，P ，N 三点共线，∴ 存在实数λ使得AP →＝λAB →＋(1－λ)AN →＝λAB →＋1－λ2AC →.又AP →＝mAB →＋14AC →，∴ ⎩⎨⎧m ＝λ，14＝1－λ2，解得m ＝12.4. 16解析：△DED 1的面积为正方形AA 1D 1D 面积的一半，三棱锥FDED 1的高即为正方体的棱长，所以VD 1DEF ＝VFDED 1＝13S △DED 1·h ＝13×12DD 1×AD ×AB ＝16.5. ⎣⎡⎦⎤3，559 解析：ω＝2x 3＋y 3x 2y ＝2x y ＋y 2x 2.令t ＝yx，画出不等式组满足的可行域如图所示，由图可知13≤t ≤2，则ω＝t 2＋2t，t ∈⎣⎡⎦⎤13，2， 令ω′＝2t －2t 2＝0，则t ＝1.ω在t ∈⎣⎡⎦⎤13，1上为减函数，在t ∈[1，2]上为增函数，t ＝1时，ω有最小值3，t ＝13时，ω有最大值559，故t 的取值范围是⎣⎡⎦⎤3，559.6. －1 解析：由题意可得f′(x)＝(2x ＋a)e x －1＋(x 2＋ax －1)e x －1＝[x 2＋(a ＋2)x ＋a －1]e x－1.因为f′(－2)＝0，所以a ＝－1，f(x)＝(x 2－x －1)e x －1，故f′(x)＝(x 2＋x －2)e x －1.令f′(x)＞0，解得x ＜－2或x ＞1，所以f(x)在(－∞，－2)，(1，＋∞)上单调递增，在(－2，1)上单调递减，所以f(x)极小值＝f(1)＝(1－1－1)e 1－1＝－1.7. 10 解析：因为对任意的正整数n ，都有2n（2n －1）（2n ＋1－1）＝12n －1－12n ＋1－1，所以⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫2n （2n －1）（2n ＋1－1）的前k 项和为 21（21－1）（22－1）＋22（22－1）（23－1）＋ (2)（2k －1）（2k ＋1－1）＝121－1－122－1＋122－1－123－1＋…＋12k －1－12k ＋1－1＝1－12k ＋1－1.令1－12k ＋1－1≥2 0182 019，即2k ＋1－1≥2 019，解得k ≥10，因此k 的最小值为10.8. [－52，1] 解析：设点P 坐标为(x ，y)，易表示出PA →＝(－12－x ，－y)，PB →＝(－x ，6－y)，则PA →·PB →＝(－12－x)(－x)＋(－y)(6－y)＝x 2＋y 2＋12x －6y ≤20. ∵ x 2＋y 2＝50，∴ 50＋12x －6y ≤20，即2x －y ＋5≤0. 又点P 在圆x 2＋y 2＝50 上，∴ 点P 在AD ︵内．由图易知，点P 横坐标的取值范围是[x C ，x D ]， 且x C ＝－5 2.联立⎩⎪⎨⎪⎧2x －y ＋5＝0，x 2＋y 2＝50，消去y ，得x 2＋4x －5＝0，解得x 1＝－5(舍去)，x 2＝1，即x D ＝1， ∴ 点P 横坐标的取值范围是[－52，1]． 9. 解：(1) 由b sin 2C ＝c sin B ，根据正弦定理，得2sin B sin C cos C ＝sin C sin B ．(2分)因为sin B>0，sin C>0，所以cos C ＝12.(4分)又C ∈(0，π)，所以C ＝π3.(6分)(2) 因为C ＝π3，所以B ∈⎝⎛⎭⎪⎫0，2π3，所以B －π3∈⎝ ⎛⎭⎪⎫－π3，π3. 又sin ⎝⎛⎭⎪⎫B －π3＝35，所以cos ⎝⎛⎭⎪⎫B －π3＝1－sin 2⎝⎛⎭⎪⎫B －π3＝45.(8分)又A ＋B ＝2π3，即A ＝2π3－B ，所以sin A ＝sin ⎝ ⎛⎭⎪⎫2π3－B ＝sin ⎣⎢⎡⎦⎥⎤π3－⎝⎛⎭⎪⎫B －π3＝sin π3cos ⎝ ⎛⎭⎪⎫B －π3－cos π3sin ⎝ ⎛⎭⎪⎫B －π3＝32×45－12×35＝43－310.(14分) 10. 解：(1) 因为矩形纸板ABCD 的面积为3 600平方厘米，故当a ＝90时，b ＝40， 从而纸盒的侧面积为S ＝2×x(90－2x)＋2×x(40－2x)＝－8x 2＋260x ，x ∈(0，20)．(3分)因为S ＝－8x 2＋260x ＝－8⎝⎛⎭⎫x －6542＋4 2252，故当x ＝654时，侧面积最大，最大值为4 2252.所以当小正方形的边长为654厘米时，纸盒的侧面积最大，为4 2252平方厘米． (6分)(2) 纸盒的体积为V ＝(a －2x)(b －2x) x ＝x[ab －2(a ＋b)x ＋4x 2]，x ∈⎝⎛⎭⎫0，b2，b ≤60.(8分) V ＝x[ab －2(a ＋b)x ＋4x 2]≤x(ab －4abx ＋4x 2) ＝x(3 600－240x ＋4x 2) ＝4x 3－240x 2＋3 600x ，(10分) 当且仅当a ＝b ＝60时等号成立．设f (x)＝4x 3－240x 2＋3 600x ，x ∈(0，30)， 则f ′(x)＝12(x －10)(x －30)．于是当0＜x ＜10时，f ′(x)＞0，所以f(x)在(0，10)上单调递增； 当10＜x ＜30时，f ′(x)＜0，所以f(x)在(10，30)上单调递减． 因此当x ＝10时，f(x)有最大值f(10)＝16 000，(12分) 此时a ＝b ＝60，x ＝10.所以当a ＝b ＝60，x ＝10时纸盒的体积最大，且最大值为16 000立方厘米．(14分) 11. 证明：(1) 设A(x 1，y 1)，B(x 2，y 2)，则x 214＋y 213＝1，x 224＋y 223＝1.两式相减，并由y 1－y 2x 1－x 2＝k ，得x 1＋x 24＋y 1＋y 23·k ＝0.(4分)由题设知x 1＋x 22＝1，y 1＋y 22＝m ，于是k ＝－34m①.由题设，得0＜m ＜32，故k ＜－12.(6分)(2) 由题意，得F(1，0)，设P(x 3，y 3)，则(x 3－1，y 3)＋(x 1－1，y 1)＋(x 2－1，y 2)＝(0，0)．由(1)及题设，得x 3＝3－(x 1＋x 2)＝1，y 3＝－(y 1＋y 2)＝－2m ＜0.又点P 在椭圆C 上，所以m ＝34，从而P ⎝⎛⎭⎫1，－32，|FP →|＝32.于是|FA →|＝（x 1－1）2＋y 21＝（x 1－1）2＋3⎝⎛⎭⎫1－x 214＝2－x12.(10分) 同理|FB →|＝2－x 22.所以|FA →|＋|FB →|＝4－12(x 1＋x 2)＝3.故2|FP →|＝|FA →|＋|FB →|，即|FA →|，|FP →|，|FB →|成等差数列．设该数列的公差为d ，则2|d|＝||FB →|－|FA →|| ＝12|x 1－x 2|＝12（x 1＋x 2）2－4x 1x 2 ②. 将m ＝34代入①，得k ＝－1.(12 分)所以直线l 的方程为y ＝－x ＋74，代入C 的方程并整理，得7x 2－14x ＋14＝0.故x 1＋x 2＝2，x 1x 2＝128，代入②解得|d|＝32128.所以该数列的公差为32128或－32128.(16 分)12. (1) 解：设等差数列{a n }的公差为d.因为无穷数列{a n }的各项均为互不相同的正整数，所以a 1∈N *，d ∈N *. ① 由a 2＝5，S 5＝40，得a 1＋d ＝5，5a 1＋5×42d ＝40，(2分)解得a 1＝2，d ＝3.所以b 2＝S 2a 2－1＝a 1a 2＝25.(4分)② 因为数列{b n }为等差数列，所以2b 2＝b 1＋b 3，即2⎝⎛⎭⎫S 2a 2－1＝S 1a 1－1＋S3a 3－1. 所以2（2a 1＋d ）a 1＋d ＝1＋3（a 1＋d ）a 1＋2d ，解得a 1＝d (d ＝0舍去)．(6分)此时，b n ＝S na n －1＝n （n ＋1）2a 1na 1－1＝n －12.(8分)(2) 证明：因为aa 1＋1＝a 1＋[(a 1＋1)－1]d 是数列{a n }的第(a 1＋1)项，aa 1(d ＋2)＋1＝a 1＋{[a 1(d ＋2)＋1]－1}d 是{a n }的第[a 1(d ＋2)＋1]项，且(aa 1＋1)2＝a 21(1＋d )2，a 1·aa 1(d ＋2)＋1＝a 1·[a 1＋a 1(d ＋2)d ]＝a 21(1＋d 2)，所以(aa 1＋1)2＝a 1·aa 1(d ＋2)＋1.又a 1＜a 1＋1＜a 1(d ＋2)＋1，所以数列{a n }中存在三项a 1，aa 1＋1，aa 1(d ＋2)＋1成等比数列．(16 分)。

毛额市鹌鹑阳光实验学校平鲁区李林中学高考英语综合考查小卷子6一：单项选择：（20分）1.-----Bruce, please don’t open the door. It’s cold.-----Pardon.------I ___ you not to open the door.A.will tellB. had toldC. have toldD. told2. I arrived____ at the company, but luckily the meeting had been delayed.A. lateB. latelyC. laterD. latest3.Many fantasy movies have at least one or two scenes that ___ filmed in Avalon.A. will beB. have beenC. wasD. were4. ----It is not____ for you to wear a cap while eating.---Oh, I’m sorry. I wasn’t thinkingA. properB. usualC. commonD. casual5.____ from the mistakes of others----you can never live long enough to make them all yourself.A. To learnB. LearnC. LearningD. Having learned6.____ like the native speakers, you have to listen to what they say and read what they write.A. TalkingB. To talkC. Having talkedD. Talk7.Before the conference was over, the organizer asked the specialists ____ for distinguished achievements to pose for a group photo.A. honorB. to honorC. honoredD. honoring8. Don’t’ expect to master a language in a short time. You can’t spend ___ much time practicing it.A. tooB. veryC. soD. as9. ---What a golden opportunity you missed!. It means you will have to wait for another ten years.----But I ____to Beijing on business.A.travelB. would travelC. have travelledD. was traveling10. I don’t like the weather in the north as it___ be quite windy, especially in spring.A. mustB. canC. shouldD. would11. The government has ___ measures to improve the working conditionsA. adaptedB. allowedC. adoptedD. afforded12. Jack had travelled six miles across the Channel ___ his engine failed and was forced to land on the sea.A. whileB. untilC. afterD. when13. Jane was holidaying in a wildlife park ____ she was bitten on the leg by a lion.A. whenB. whileC. sinceD. once14. How can he learn English well ___ he has no interest in it?A. asB. whileC. whenD. because15. The police arrived, after ___ the situation became peaceful.A. thatB. whichC. thenD. Whom16. Most children in Britain are educated at public _____.A. costB.price C.expense D. salary17. --- You don’t like this oil painting, do you?---_____. I like it better _____ I look at it.A. Yes, the momentB. No, asC. No, whenD. Yes, the more18. Dr Brown has the habit of _____ the room when he is thinking about something troublesome.A. pacingB.stepping C. walking D. marching19. It was until October that they _____.A. finished their long journeyB. paid off the debtsC. reached anagreement D. worked on the project20. When a giraffe(长颈鹿) has ____ drink, it has to stand with its front legs wide apart in order to reach ______ water.A. /; /B. a; theC. the;/ D. /; the三：信息匹配（每题2分，共10分）The first thing you need to come up with is an idea for your club.22 Pets, clothes, pop music or dancing groups, sports, making things? The list is endless.Next you need some friends to be in your club with you. 23 . All you need is three or four other people who are interested in the same thing as you.24 .You should all sit down somewhere together with lots of piecesof paper and write down every name you can think up. That’ll keep you busy for ages.At your first meeting you should make up a rule book. And the first rule should be no grown-ups or little/big brothers or sisters! The best clubs are always secret!Now you have just about everything you need, except membership cards. These are very important and again you can spend a lot of time making them. 25 Why not leave some space for a photo of yourself? That will make the membership card really look like it.So there you are, get clubbing! Once you get started you’ll thinkof loads of more interesting things to do!A. That’s easy.B. Enjoy your own club!C. Invite a designer to join you.D. What are you inte rested in?E. Some vacation is just around the corner.F. Then you need to pick a name for your club.G. Use a bright thick pen to make a special design.小卷子8： DADAB BCADB CDACB CDADB【答案】EDAFG。

【最新】安徽高考语文二轮限时综合小练6练习卷学校:___________姓名：___________班级：___________考号：___________一、选择题1．下列词语中，字形全都正确的一组是 ( ) A．蕴藉/慰藉工夫/功夫茶轶事/卷帙浩繁B．振幅/辐射照相/摄像机汇合/融汇贯通C．诀窍/抉择叶片/百页窗部署/按部就班D．搏弈/脉搏掉价/掉书袋倍加/备尝艰辛2．下列各句中，没有语病的一句是() A．现在最重要的是如何治理并重视环境问题，因为“美丽中国”必然是一个山清水秀的中国，而不是一个迷雾重重的中国。

B．城乡居民的身份平等将是户籍改革的最终目标，户籍改革的关键在于破除二元结构，逐步取消农村户口十分重要。

C．在危难时刻，张丽莉老师临危不惧、挺身而出、舍己救人的英雄壮举，是用大爱谱写的一曲生命的赞歌，是用鲜血和生命塑造的新时期优秀人民教师的楷模。

D．当时间的钟摆标注出全面小康的崭新目标，面对市场化、信息化、民主化的大潮涌动，如何读懂人民的期待，无疑是必须深思的首要课题。

3．依次填入下面一段文字横线处的语句，衔接最恰当的一组是( )朴学又称考据学。

清代朴学的兴起，首先与清代文化的高度成熟关系密切，________，________，________，________，________，________，这种学术上的争论最终促进了朴学的繁荣。

①清代人认为宋明理学空谈义理，把儒家治国平天下的传统丢掉了②文化高度成熟的一个表现是图书典籍的极大丰富③要想真正把握孔孟的精神，只有回到儒家原典中去寻找依据④这直接带来了清代图书事业的繁荣⑤学术界对宋明理学的反对，也是其兴起的重要原因⑥随之而来的是一些人专注于校勘、辨伪工作，从事文字训诂的学者越来越多A．②④⑥⑤①③ B．②④⑥⑤③①C．⑤①③④②⑥ D．⑤③①④②⑥二、文言文阅读阅读下面的文言文，完成小题。

魏主①以平城地寒，六月雨雪，风沙常起，将迁都洛阳；恐群臣不从，乃议大举伐齐，欲以胁众。

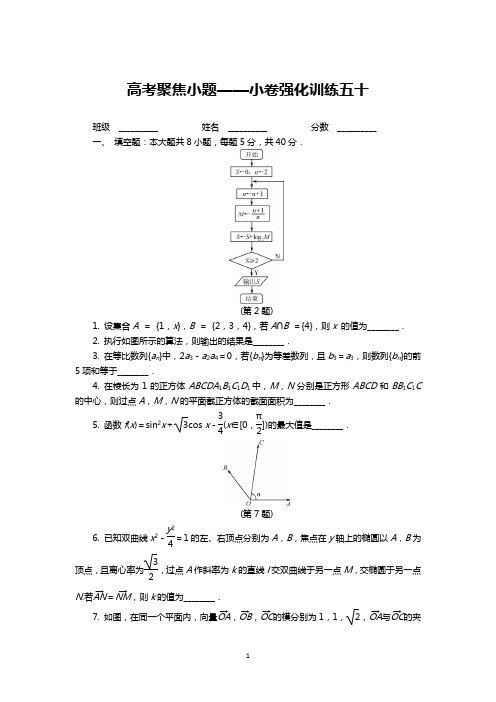
高考聚焦小题——小卷强化训练五十班级 __________ 姓名 __________ 分数 __________ 一、 填空题：本大题共8小题，每题5分，共40分．(第2题)1. 设集合A ＝ {1，x }，B ＝ {2，3，4}，若A ∩B ＝{4}，则x 的值为________．2. 执行如图所示的算法，则输出的结果是________．3. 在等比数列{a n }中，2a 3－a 2a 4＝0，若{b n }为等差数列，且b 3＝a 3，则数列{b n }的前5项和等于________．4. 在棱长为1的正方体ABCDA 1B 1C 1D 1中，M ，N 分别是正方形ABCD 和BB 1C 1C 的中心，则过点A ，M ，N 的平面截正方体的截面面积为________．5. 函数f (x )＝sin 2x ＋3cos x －34(x ∈[0，π2])的最大值是________．(第7题)6. 已知双曲线x 2－y 24＝1的左、右顶点分别为A ，B ，焦点在y 轴上的椭圆以A ，B 为顶点，且离心率为32，过点A 作斜率为k 的直线l 交双曲线于另一点M ，交椭圆于另一点N .若AN →＝NM →，则k 的值为________．7. 如图，在同一个平面内，向量OA →，OB →，OC →的模分别为1，1，2，OA →与OC →的夹角为α，且tan α＝7，OB →与OC →的夹角为45°.若OC →＝mOA →＋nOB →(m ，n ∈R )，则m ＋n ＝________．8. 设函数f (x )＝log 22x 2x 2＋1(x ＞0)．若函数g (x )＝||f （x ）2＋m ||f （x ）＋2m ＋3有三个零点，则实数m 的最大值为________．二、 解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤．9. (本小题满分14分)在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且cos A ＝35，tan(B －A )＝13.(1) 求tan B 的值；(2) 若c ＝13，求△ABC 的面积.如图，有一景区的平面图是一半圆形，其中AB长为2 km，C，D两点在半圆弧上，满足BC＝CD，设∠COB＝θ.(1) 现要在景区内铺设一条观光道路，由线段AB，BC，CD和DA组成，则当θ为何值时，观光道路的总长l最长？并求l的最大值；(2) 若要在景区内种植鲜花，其中在△AOD和△BOC内种满鲜花，在扇形COD内种一半面积的鲜花，则当θ为何值时，鲜花种植面积S最大？如图，在平面直角坐标系xOy 中，已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)的离心率为23，C 为椭圆上位于第一象限内的一点．(1) 若点C 的坐标为(2，53)，求a ，b 的值；(2) 设A 为椭圆的左顶点，B 为椭圆上一点，且AB →＝12OC →，求直线AB 的斜率．已知函数f(x)＝x2＋ax(a∈R)，g(x)＝ln x.(1) 求证：g(x)＜x2；(2) 设h(x)＝f(x)＋bg(x)(b∈R)，若a2＋b＝0，且当x＞0时h(x)＞0恒成立，求a的取值范围．小卷强化训练五十1. 4 解析：因为A ∩B ＝{4}，所以4∈A ，故x ＝4.2. 2 解析：根据循环，依次得到n ，M ，S 的值分别为3，43，log 243；4，54，log 243＋log 254；…；11，1211，log 243＋log 254＋…＋log 21211.因为S ＝log 243＋log 254＋…＋log 21211＝2≥2，所以最后的输出结果为2.3. 10 解析：由等比中项的性质，得2a 3－a 2a 4＝2a 3－a 23＝a 3(2－a 3)＝0，显然a 3≠0，所以a 3＝2，所以b 3＝2，故数列{b n }的前5项和为52(b 1＋b 5)＝52×2b 3＝5b 3＝10.4. 32 解析：可知截面是等边三角形AB 1C ，且边长为2，因此截面面积为S △AB 1C＝12×(2)2×sin 60°＝32. 5. 1 解析：f(x)＝sin 2x ＋3cos x －34＝1－cos 2x ＋3cos x －34＝－cos 2x ＋3cos x ＋14⎝ ⎛⎭⎪⎫x ∈⎣⎢⎡⎦⎥⎤0，π2， 令cos x ＝t ，则t ∈[0，1]，y ＝－t 2＋3t ＋14＝－⎝⎛⎭⎫t －322＋1，所以当t ＝32，即x ＝π6时，f(x)取最大值，且最大值为1.6. ±233 解析：对于椭圆，显然b ＝1，c a ＝32，所以椭圆方程为y 24＋x 2＝1.设N(x 0，y 0)，则由AN →＝NM →，得M(2x 0＋1，2y 0)．因为点M 在双曲线上，点N 在椭圆上，所以y 204＋x 20＝1，(2x 0＋1)2－4y 204＝1，解得x 0＝12，y 0＝±3(x 0＝－1，y 0＝0舍去)，故直线l 的斜率k ＝±233.7. 3 解析：(解法1)由题意，得 ⎩⎨⎧OC →·OA →＝mOA →·OA →＋nOB →·OA →，OC →·OB →＝mOA →·OB →＋nOB →·OB →(*)．而由tan α＝7，得sin α＝752，cos α＝152，所以OA →·OB →＝1×1×cos ⎝ ⎛⎭⎪⎫α＋π4＝cos αcos π4－sin αsin π4＝－35，OC →·OA →＝2cos α＝15，OC →·OB →＝2×1×22＝1，所以(*)式可化简为⎩⎨⎧15＝m －35n ①，1＝－35m ＋n ②，①＋②，得m ＋n ＝3.(解法2：坐标法)如图，以OA 所在的直线为x 轴，过点O 且垂直于OA 的直线为y 轴建立平面直角坐标系．由题意结合解法1可得A(1，0)，C ⎝⎛⎭⎫15，75，B ⎝⎛⎭⎫－35，45.由OC →＝mOA →＋nOB →，得⎝⎛⎭⎫15，75＝m(1，0)＋n ⎝⎛⎭⎫－35，45，即⎩⎨⎧15＝m －35n ，75＝45n ，解得⎩⎨⎧m ＝54，n ＝74，故m ＋n ＝3.(解法3：解三角形)由tan α＝7，得sin α＝7210，cos α＝210.如图，根据向量的分解，得⎩⎪⎨⎪⎧n cos 45°＋m cos α＝2，n sin 45°－m sin α＝0，即⎩⎨⎧22n ＋210m ＝2，22n －7210m ＝0，即⎩⎪⎨⎪⎧5n ＋m ＝10，5n －7m ＝0，解得m ＝54，n ＝74，所以m ＋n ＝3.8. －43 解析：因为2x 2x 2＋1＝2（x 2＋1）－2x 2＋1＝2－2x 2＋1，所以当x ＞0时，0＜2－2x 2＋1＜2，即f(x)＜1，则y ＝|f(x)|的大致图象如图所示，设|f(x)|＝t ，则函数g(x)＝|f(x)|2＋m|f(x)|＋2m ＋3有三个零点，即为t 2＋mt ＋2m ＋3＝0有两个根，且一个在(0，1)上，一个在[1，＋∞)上．设h(t)＝t 2＋mt ＋2m ＋3.① 当有一个根为1时，h(1)＝1＋m ＋2m ＋3＝0，解得m ＝－43，此时另一根为13，满足条件；② 当两个根都不是1时，则满足⎩⎪⎨⎪⎧h （0）＞0，h （1）＜0，所以⎩⎪⎨⎪⎧2m ＋3＞0，1＋m ＋2m ＋3＜0，即⎩⎨⎧m ＞－32，m ＜－43，所以－32＜m ＜－43.综上，－32＜m ≤－43，即实数m 的取值范围是⎝⎛⎦⎤－32，－43，所以实数m 的最大值为－43.9. 解：(1) 在△ABC 中，由cos A ＝35，得sin A ＝1－cos 2A ＝45，所以tan A ＝sin A cos A ＝43.(2分)所以tan B ＝tan [(B －A)＋A]＝tan （B －A ）＋tan A 1－tan （B －A ）·tan A ＝13＋431－13×43＝3. (6分)(2) 在△ABC 中，由tan B ＝3，得 sin B ＝31010，cos B ＝1010，(8分)则sin C ＝sin (A ＋B)＝sin A cos B ＋cos A sin B ＝131050.(10分)由正弦定理b sin B ＝c sin C ，得b ＝c sin Bsin C ＝13×31010131050＝15.(12分)所以△ABC 的面积S ＝12bc sin A ＝12×15×13×45＝78. (14分)10. 解：(1) 由题意，得∠COB ＝θ，∠AOD ＝π－2θ，θ∈⎝ ⎛⎭⎪⎫0，π2.如图，取BC 的中点M ，连结OM ，则OM ⊥BC ，∠BOM ＝θ2，所以CD ＝BC ＝2BM ＝2sin θ2.同理可得AD ＝2sin π－2θ2＝2cos θ，所以l ＝2＋2sin θ2＋2sin θ2＋2cos θ＝2⎝⎛⎭⎪⎫1－2sin 2θ2＋4sin θ2＋2，即l ＝－4⎝ ⎛⎭⎪⎫sin θ2－122＋5，θ∈⎝⎛⎭⎪⎫0，π2.所以当sin θ2＝12，即θ＝π3时，观光道路的总长最长，为5 km .(6分)(2) 因为S △BOC ＝12sin θ，S △AOD ＝12sin (π－2θ)＝sin θcos θ，S 扇形COD ＝12θ，所以S ＝12sin θ＋sin θcos θ＋14θ，所以S′＝12cos θ＋cos 2θ－sin 2θ＋14＝14(4cos θ＋3)·(2cos θ－1)．(10分)因为θ∈⎛⎪⎫0，π，由S′＝0，得θ＝π3，列表如下：所以当θ＝π3时，鲜花种植面积S 取得最大值. (14分)11. 解：(1) 因为椭圆的离心率为23，所以a 2－b 2a ＝23，即b 2a 2＝59①.因为点C ⎝⎛⎭⎫2，53在椭圆上，所以4a 2＋259b 2＝1 ②.(3分) 由①②解得a 2＝9，b 2＝5.因为a ＞b ＞0，所以a ＝3，b ＝ 5.(6分) (2) 由(1)知b 2a 2＝59，所以椭圆方程为x 2a 2＋9y 25a 2＝1，即5x 2＋9y 2＝5a 2.设直线OC 的方程为x＝my(m ＞0)，B(x 1，y 1)，C(x 2，y 2)．由⎩⎪⎨⎪⎧x ＝my ，5x 2＋9y 2＝5a 2，得5m 2y 2＋9y 2＝5a 2， 所以y 2＝5a 25m 2＋9.因为y 2＞0，所以y 2＝5a 5m 2＋9.(10分)因为AB →＝12OC →，所以AB ∥OC.可设直线AB 的方程为x ＝my －a.由⎩⎪⎨⎪⎧x ＝my －a ，5x 2＋9y 2＝5a 2，得(5m 2＋9)y 2－10amy ＝0，所以y ＝0或y ＝10am 5m 2＋9，得y 1＝10am 5m 2＋9.(12分)因为AB →＝12OC →，所以(x 1＋a ，y 1)＝⎝⎛⎭⎫12x 2，12y 2，于是y 2＝2y 1， 即5a 5m 2＋9＝20am 5m 2＋9(m ＞0)，解得m ＝35.所以直线AB 的斜率为1m ＝533.(16分)12. (1) 证明：设h(x)＝x 2－g(x)＝x2－ln x ，则h′(x)＝x －22x ，于是h(x)在(0，2)上单调递减，在(2，＋∞)上单调递增，(3分)于是h(x)min ＝h(2)＝1－ln 2＞0，从而h(x)＞0恒成立，即g(x)＜x2.(6分)(2) 解：h(x)＝f(x)＋bg(x)＝x 2＋ax ＋b ln x. 因为a 2＋b ＝0，所以h(x)＝x 2＋ax －a 2ln x ， 所以h′(x)＝（x ＋a ）（2x －a ）x .(8分)当a ＝0时，h(x)＝x 2＞0恒成立；(10分)当a ＞0时，h(x)在⎝⎛⎭⎫0，a 2上单调递减，在⎝⎛⎭⎫a 2，＋∞上单调递增，于是h(x)min ＝h ⎝⎛⎭⎫a2＞0， 即34a 2－a 2ln a2＞0，解得0＜a ＜2e 34.(12分) 当a ＜0时，h(x)在(0，－a)上单调递减，在(－a ，＋∞)上单调递增，于是h(x)min ＝h(－a)＞0，即－a 2ln (－a)＞0，解得－1＜a ＜0. 综上，a 的取值范围是(16分)。

温馨提示：此套题为Word版，请按住Ctrl,滑动鼠标滚轴，调节合适的观看比例，答案解析附后。

关闭Word文档返回原板块。

课时提升作业(二十八)选修6 Unit 3Ⅰ. 单项填空1. (2018·杭州模拟)The premier the importance of developing Chinese economy in his speech at University of Cambridge.A. approvedB. devotedC. realizedD. stressed2. The leader his basketball team by bringing in several young players.A. weakenedB. strengthenedC. quittedD. banned3. (2018·温州模拟)I am told that the new law will come into on January 1st next year.A. effectB. useC. serviceD. existence4. He felt of cheating in the exam, deciding never to do such things again.A. shameB. ashamedC. sorryD. shameful5. It is reported that the accident careless driving, so a lot of money be paid by the driver.A. was due to; was due toB. due to; was due toC. is due to; was due toD. is due to; due to6. (2018·徐州模拟)A great many teenagers became playing computer games, wasting their precious time.A. accustomed toB. addicted toC. used toD. due to7. —There are too many people in the building during the daytime.—Yes, that’s a serious threat to safety fire or other disasters.A. in case ofB. in spite ofC. in view ofD. in place of8. (2018·黄冈模拟)After all, preferring peaceful means does not mean China will put _______ its own sovereignty and territorial integrity(主权和领土完整).A. at heartB. at handC. at mostD. at risk9. If you do it without others’ help, you will only difficulty.A. turn intoB. put intoC. get intoD. break into10. He his position as president by giving jobs to his friends in exchange for money.A. gainedB. changedC. abusedD. refused11. —Do you feel like ?—No, but I’d like today.A. to skate; skateB. skating; skatingC. skating; to skateD. to skate; skating12. —Do you think worthwhile to go all the way to Beijing to buy that computer?—Well, I’m going to visit the Bird’s Nest and the Water Cube.A. itB. /C. thisD. that13. (2018·西宁模拟) has been announced, we shall have our final exams next month.A. ThatB. WhatC. ItD. As14. (2018·南平模拟)An awful accident, however, occur again at the railroad crossing the other day.A. didB. doesC. has toD. had to15. It was a(n) situation, because the restaurant was too expensive for us but we didn’t want to just leave.A. amazingB. curiousC. desperateD. awkwardⅡ. 完形填空A woman told about her experience as a child when her try at baking a cake for her dad ended in a failure. Instead of 1 her, her father praised her a lot. It was a life lesson for that lady. It improved her self-esteem(自尊心)so that she had the 2 to try new things without the fear of failure.When I read about that, my mind went 3 over to a lazy summer afternoon many years ago. Our family of four were enjoying ourselves, 4 on the grass. Daddy made a 5 , and we all laughed. Then Daddy glanced at me and said, “Karen, run up to the house and 6 me a cheese sandwich. ”I jumped up happily and 7 our lawn and went into the kitchen and gathered the ingredients(原料). Feeling like a(n) 8 girl, I ran back across the yard and 9 handed my creation to Daddy, who took a big 10 . As he chewed(咀嚼), he asked, “Did you wash your hands first?”“No, sir, ” I answered. I hadn’t11 thought about it. He spit the chewed-up food out onto the ground as he threw the sandwich into the air. Cheese and bread 12 everywhere. “Now, go back to the house, wash your hands, and fix me another 13 , ” he said.I turned and walked slowly across the yard, 14 not to cry, torn between hurt and anger. The15 no longer seemed so beautiful.That was one of the first times in my life that my father made me feel 16 , but it certainly wasn’t the last. In his later years, my dad became much gentler. He 17 me and showed his love to me in different ways. But I 18 : what if Dad had dealt with the incident in a 19 way, like the father whose daughter 20 in her cake baking?(275W)1. A. punishing B. missing C. reminding D. warning2. A. plan B. idea C. courage D. order3. A. up B. back C. down D. ahead4. A. standing B. hiding C. moving D. lying5. A. song B. cry C. joke D. film6. A. pass B. fix C. offer D. buy7. A. ran across B. turned over C. left for D. arrived at8. A. beautiful B. anxious C. big D. honest9. A. secretly B. luckily C. slowly D. proudly10. A. bite B. step C. mouth D. hand11. A. still B. even C. also D. yet12. A. walked B. watched C. ran D. flew13. A. sugar B. cake C. sandwich D. snack14. A. struggling B. agreeing C. learning D. pretending15. A. lawn B. day C. kitchen D. sky16. A. happy B. excited C. interested D. uncomfortable17. A. brought B. found C. supported D. followed18. A. promise B. wonder C. admit D. advise19. A. positive B. silent C. strict D. special20. A. stayed B. succeeded C. appeared D. failedⅢ. 短文改错(2018·宁波模拟) 下面短文中有10处语言错误。

2018届高一（20、21）班周末语文综合小题训练（六）参考答案1.选B。

（A项“属”读zhǔ；C项“扁”读piān；D项“樵”读qiáo。

）2.选D。

（A项急—激，聘—骋，序—叙；B项取—趣，凫凫—袅袅，弦—舷；C项凭—冯，偏—扁。

）3.选A。

【解析】A项，鱼目混珠：比喻假的东西冒充真的东西，使用正确。

B项，扫眉才子：指有文采的女子，使用对象错误。

C项，念念不忘：指牢记在心，时刻不忘，与“时刻”重复。

D项，长袖善舞：多用来形容有财势、有手腕的人善于钻营取巧，感情色彩不当。

4.选A。

【解析】此类词语使用判断的题目，要在整体把握句意的情况下，根据语境，结合着成语的解释来判断。

尔虞我诈：表示彼此互相欺骗。

钩心斗角：比喻用尽心机，明争暗斗。

拭目以待：擦亮眼睛等待着，形容殷切期望或密切关注事态的动向及结果。

刮目相看：指别人已有进步，不能再用老眼光去看他。

5.选D。

【解析】此类型题首先要通读语段，了解句意，然后注意句与句的排列组合，注意上下句的衔接、呼应，做到话题统一，句序合理，衔接和呼应自然。

要加强对语境的分析与体会。

有些题应注意排序句的逻辑顺序和句中关联词语的运用。

分析可知，⑥③相连，先从反面说人们生存必须的吃饭、喝水、呼吸空气等方面，然后说⑤空气恶化现象，以及①④②恶果。

6.选C。

【解析】A 两面对一面；B“预先预测”重复；D“一旦……后”句式杂糅。

辨析病句的十个看点：⑴看两面词，有些句子的语病往往就在两面词上，句子中如果出现“能否”“是否”“有没有”“能不能”“成败”“好坏”“优劣”这类词；我们就要仔细分析该句是否有“一面对两面”或“两面对一面”的语病。

⑵看代词，病句试题中，如出现代词，我们要特别注意。

要看清代词指代的对象。

⑶看介词，由于滥用介词和介词……方位词格式，易造成主语残缺或主客体颠倒等语病。

因此我们要看清介词和介词短语的使用。

⑷看否定词，很多句子的语病出现在否定词上，常见错误有多重否定中由于多用了否定词，而表意相反了，或者多重否定句与反问句连用造成表意不符。

高考聚焦小题——小卷强化训练十三班级 __________ 姓名 __________ 分数 __________ 一、 填空题：本大题共8小题，每题5分，共40分．(第3题)1. 已知复数z ＝2＋i1－i (i 为虚数单位)，那么z 的共轭复数为________．2. 若tan(α－π4)＝16，则tan α＝________．3. 执行如图所示的程序框图，若a ＝2 018，则输出的S ＝________．4. 设等边三角形ABC 的边长为1，t 为任意的实数，则|AB →＋tAC →|的最小值为________． 5. 已知函数f (x )＝2sin x ＋1(x ∈[0，2π])，设h (x )＝|f (x )|－a ，则当1<a <3时，函数h (x )的零点个数为________．6. 已知函数f (x )＝(x 2－2x )sin(x －1)＋x ＋1在x ∈[－1，3]上的最大值为M ，最小值为m ，则M ＋m ＝________．7. 已知x ＞y ＞0，且x ＋y ≤2，则4x ＋3y ＋1x －y的最小值为________．8. 设椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2.若椭圆上恰好有6个不同的点P ，使得△F 1F 2P 为等腰三角形，则椭圆C 的离心率的取值范围是______________．二、 解答题：本大题共4小题，共60分．解答时应写出必要的文字说明、证明过程或演算步骤．9. (本小题满分14分)如图，在四棱锥PABCD 中，底面ABCD 是矩形，PD ⊥平面ABCD ，过AD 的平面分别与PB ，PC 交于点E ，F .求证：(1) 平面PBC ⊥平面PCD ；(2) AD∥EF.已知椭圆C：x2a2＋y2b2＝1(a＞b＞0)的离心率为32，且点(－3，12)在椭圆C上．(1) 求椭圆C的标准方程；(2) 若直线l交椭圆C于P，Q两点，线段PQ的中点为H，O为坐标原点，且OH＝1，求△POQ面积的最大值．如图，圆O 是一块半径为1米的圆形钢板，为生产某部件需要，需从中截取一块多边形ABCDFGE .其中AD 为圆O 的直径，点B ，C ，G 在圆O 上，BC ∥AD ，点E ，F 在AD 上，且OE ＝OF ＝12BC ，EG ＝FG .(1) 设∠AOB ＝θ，试将多边形ABCDFGE 面积S 表示成θ的函数关系式； (2) 求多边形ABCDFGE 面积S 的最大值．已知数列{a n }与{b n }的前n 项和分别为A n 和B n ，且对任意n ∈N *，a n ＋1－a n ＝2(b n ＋1－b n )恒成立．(1) 若A n ＝n 2，b 1＝2，求B n ； (2) 若对任意n ∈N *，都有a n ＝B n 及b 2a 1a 2＋b 3a 2a 3＋b 4a 3a 4＋…＋b n ＋1a n a n ＋1<13恒成立，求正实数b 1的取值范围；(3) 若a 1＝2，b n ＝2n ，是否存在两个互不相等的整数s ，t (1<s <t )，使A 1B 1，A sB s，A t B t成等差数列？若存在，求出s ，t 的值；若不存在，请说明理由．小卷强化训练十三1. 12－32i 解析：z ＝2＋i 1－i ＝（2＋i ）（1＋i ）（1－i ）（1＋i ）＝1＋3i 2＝12＋32i ，则z ＝12－32i . 2. 75 解析：tan α＝tan ⎝ ⎛⎭⎪⎫α－π4＋π4＝tan ⎝ ⎛⎭⎪⎫α－π4＋11－tan ⎝ ⎛⎭⎪⎫α－π4＝16＋11－16＝75. 3. 4 0372 019 解析：由流程图知，该算法求的是S ＝1＋11×2＋12×3＋…＋1k （k ＋1）＝1＋1－12＋12－13＋…＋1k －1k ＋1＝2－1k ＋1.又a ＝2 018，∴ 当k ＝2 019时，退出循环，此时S ＝2－12 018＋1＝4 0372 019. 4. 32解析：令a ＝AB →，b ＝AC →，则|a|＝|b|＝1，a ，b 的夹角为60°，于是|AB →＋tAC →|2＝|a ＋t b |2＝a 2＋t 2b 2＋2t a·b ＝t 2＋t ＋1＝⎝⎛⎭⎫t ＋122＋34≥34.所以|AB →＋tAC →|的最小值为32.5. 2 解析：作出函数y 1＝|f(x)|的图象，令y 2＝a ，则当1<a<3时，由数形结合，不难发现，函数y 1，y 2有两个交点，即函数h(x)的零点个数为2.6. 4 解析：设t ＝x －1，则f(x)＝(x 2－2x)sin (x －1)＋x ＋1＝(t 2－1)sin t ＋t ＋2，t ∈[－2，2]．记g(t)＝(t 2－1)·sin t ＋t ＋2，则函数y ＝g(t)－2＝(t 2－1)sin t ＋t 是奇函数，由已知y ＝g(t)－2的最大值为M －2，最小值为m －2，所以M －2＋(m －2)＝0，即M ＋m ＝4.7. 94 解析：由x ＞y ＞0可得x ＋3y ＞0，x －y ＞0，[(x ＋3y)＋(x －y)]⎝ ⎛⎭⎪⎫4x ＋3y ＋1x －y ＝5＋4（x －y ）x ＋3y ＋x ＋3yx －y ≥5＋24（x －y ）x ＋3y ·x ＋3y x －y ＝9，可得4x ＋3y ＋1x －y ≥9（x ＋3y ）＋（x －y ）＝92（x ＋y ）≥94.当且仅当2(x －y)＝x ＋3y ，即x ＝5y ＝53时，取得最小值94. 8. ⎝⎛⎭⎫13，12∪⎝⎛⎭⎫12，1 解析：⎩⎪⎨⎪⎧4c ＞2a －2c ，2c ≠a⇒13＜e ＜1且e ≠12，故离心率的取值范围是⎝⎛⎭⎫13，12∪⎝⎛⎭⎫12，1. 9. 证明：(1) 因为PD ⊥平面ABCD ，BC ⊂平面ABCD ， 所以PD ⊥BC.因为底面ABCD 是矩形，所以CD ⊥BC.因为CD ∩PD ＝D ，CD ，PD ⊂平面PCD ， 所以BC ⊥平面PCD.因为BC ⊂平面PBC ，所以平面PBC ⊥平面PCD.(7分) (2) 因为底面ABCD 是矩形，所以AD ∥BC. 因为BC ⊂平面PBC ，AD ⊄平面PBC ， 所以AD ∥平面PBC.因为AD ⊂平面ADFE ，平面ADFE ∩平面PBC ＝EF ，所以AD ∥EF.(14分)10. 解：(1) 由已知，得c a ＝32，3a 2＋14b 2＝1,解得a 2＝4，b 2＝1，(3分)所以椭圆C 的标准方程是x 24＋y 2＝1.(4分)(2) 设l 与x 轴的交点为D(n ，0)，直线l ：x ＝my ＋n ，与椭圆的交点为P(x 1，y 1)，Q(x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝my ＋n ，x 24＋y 2＝1，得(4＋m 2)y 2＋2mny ＋n 2－4＝0，∴ y 1＋y 2＝－2mn4＋m 2，y 1y 2＝n 2－44＋m2， ∴ y 1＋y 22＝－mn 4＋m2， ∴x 1＋x 22＝m （y 1＋y 2）＋2n 2＝4n 4＋m2， 即H ⎝ ⎛⎭⎪⎫4n 4＋m 2，－mn 4＋m 2. 由OH ＝1，得n 2＝（4＋m 2）216＋m2，(10分) 则S △POQ ＝12OD|y 1－y 2|＝12|n||y 1－y 2|.令T ＝n 2(y 1－y 2)2＝n 2[(y 1＋y 2)2－4y 1y 2]＝12×16×4＋m 2（16＋m 2）2，(11分)设t ＝4＋m 2(t ≥4)，则4＋m 2（16＋m 2）2＝t t 2＋24t ＋144＝1t ＋144t＋24≤148，当且仅当t ＝144t ，即t ＝12时等号成立，此时S △POQ ＝1，所以△POQ 面积的最大值为1.(14分) 11. 解：连结EF ，BE ，OB ，OG ，∵ OE ＝OF ＝12BC ，∴ BC ＝EF ，∴ BE ⊥EO.∵ EG ＝FG ，∴ OG ⊥EF.(1) 在Rt △BEO 中，BO ＝1，∠AOB ＝θ， ∴ EO ＝cos θ，BE ＝sin θ， ∴ BC ＝EF ＝2cos θ，∴ S ＝S 梯形ABCD ＋S △EGF ＝12(AD ＋BC)·BE ＋12EF ·OG ＝12(2＋2cos θ)sin θ＋12×2cos θ×1 ＝(sin θcos θ＋sin θ＋cos θ)平方米，θ∈⎝ ⎛⎭⎪⎫0，π2.(8分)(2) 令t ＝sin θ＋cos θ，θ∈⎝ ⎛⎭⎪⎫0，π2，则sin θcos θ＝t 2－12，且t ＝2sin ⎝ ⎛⎭⎪⎫θ＋π4∈(1，2]，∴ S ＝t 2－12＋t ＝t 22＋t －12＝12(t ＋1)2－1，t ∈(1，2]，当t ＝2，即θ＝π4时，S max ＝12＋2，即多边形ABCDFGE 面积S 的最大值为⎝⎛⎭⎫12＋2平方米．(16分)12. 解：(1) 因为A n ＝n 2，所以a n ＝⎩⎪⎨⎪⎧1，n ＝1，n 2－（n －1）2，n ≥2，即a n ＝2n －1，n ∈N *.(2分)故b n ＋1－b n ＝12(a n ＋1－a n )＝1，所以数列{b n }是以2为首项，1为公差的等差数列，所以B n ＝n ·2＋12n ·(n －1)·1＝12n 2＋32n ，n ∈N *.(4分)(2) 依题意B n ＋1－B n ＝2(b n ＋1－b n )，即b n ＋1＝2(b n ＋1－b n )，即b n ＋1b n＝2，所以数列{b n }是以b 1为首项，2为公比的等比数列，所以a n ＝B n ＝1－2n1－2·b 1＝b 1(2n －1)，(6分)所以b n ＋1a n a n ＋1＝b 1·2nb 1（2n －1）·b 1（2n ＋1－1）＝2nb 1（2n －1）·（2n ＋1－1） ＝1b 1⎝ ⎛⎭⎪⎫12n －1－12n ＋1－1，(8分) 所以b 2a 1a 2＋b 3a 2a 3＋b 4a 3a 4＋…＋b n ＋1a n a n ＋1＝1b 1(121－1－12n ＋1－1)，所以1b 1⎝ ⎛⎭⎪⎫1－12n ＋1－1<13恒成立， 即b 1>3⎝ ⎛⎭⎪⎫1－12n ＋1－1，所以b 1≥3.故正实数b 1的取值范围是[3，＋∞)．(10分) (3) 由a n ＋1－a n ＝2(b n ＋1－b n )，得a n ＋1－a n ＝2n ＋1，所以当n ≥2时，a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 3－a 2)＋(a 2－a 1)＋a 1 ＝2n ＋2n －1＋…＋23＋22＋2＝2n ＋1－2， 当n ＝1时，上式也成立，所以A n ＝2n ＋2－4－2n ，又B n ＝2n ＋1－2，所以A n B n＝2n ＋2－4－2n 2n ＋1－2＝2－n 2n －1.(12分)假设存在两个互不相等的整数s ，t (1<s <t )，使A 1B 1，A s B s ，A tB t成等差数列，等价于121－1，s 2s －1，t 2t －1成等差数列，即2s 2s －1＝121－1＋t 2t －1，即2s 2s －1＝1＋t2t －1.因为1＋t 2t －1>1，所以2s2s －1>1，即2s <2s ＋1.(14分)令h (s )＝2s －2s －1(s ≥2，s ∈N *)，则h (s ＋1)－h (s )＝2s －2>0，所以h (s )递增． 若s ≥3，则h (s )≥h (3)＝1>0，不满足2s <2s ＋1，所以s ＝2， 代入2s 2s －1＝121－1＋t2t －1，得2t －3t －1＝0(t ≥3)，当t ＝3时，显然不符合要求；当t ≥4时，令φ(t )＝2t －3t －1(t ≥4，t ∈N *)，同理可证φ(t )递增，所以φ(t )≥φ(4)＝3>0， 所以不符合要求．所以不存在正整数s ，t (1<s <t )，使A 1B 1，A s B s ，A tB t 成等差数列．(16分)。