电子科大图论-第二次作业(4、5章)-答案

电子科技大学研究生试题《图论及其应用》(参考答案)考试时间：120分钟一．填空题(每题3分，共18分)1．4个顶点的不同构的简单图共有__11___个；2．设无向图G 中有12条边，已知G 中3度顶点有6个，其余顶点的度数均小于3。

则G 中顶点数至少有__9___个；3．设n 阶无向图是由k(k ?2)棵树构成的森林，则图G 的边数m= _n-k____;4．下图G 是否是平面图？答__是___; 是否可1-因子分解？答__是_.5．下图G 的点色数=)(G χ______, 边色数=')(G χ__5____。

图G二．单项选择(每题3分，共21分)1．下面给出的序列中，是某简单图的度序列的是( A )(A) (11123); (B) (233445); (C) (23445); (D) (1333).2．已知图G 如图所示，则它的同构图是（ D ）3． 下列图中，是欧拉图的是（ D ）4． 下列图中，不是哈密尔顿图的是（B ）5． 下列图中，是可平面图的图的是（B ）AC DA B CD6．下列图中，不是偶图的是（ B ）7．下列图中，存在完美匹配的图是（B ）三．作图(6分)1．画出一个有欧拉闭迹和哈密尔顿圈的图；2．画出一个有欧拉闭迹但没有哈密尔顿圈的图；3．画出一个没有欧拉闭迹但有哈密尔顿圈的图；解： 四．(10分)求下图的最小生成树，并求其最小生成树的权值之和。

解：由克鲁斯克尔算法的其一最小生成树如下图：权和为：20.五．(8分)求下图G 的色多项式P k (G).解：用公式(G P k -G 的色多项式：)3)(3)()(45-++=k k k G P k 。

六．(10分) 22，n 3个顶点的度数为3，…，n k 个顶点的度数为k ，而其余顶点的度数为1，求1度顶点的个数。

解：设该树有n 1个1度顶点，树的边数为m.一方面：2m=n 1+2n 2+…+kn k另一方面：m= n 1+n 2+…+n k -1 v v 13图G由上面两式可得：n 1=n 2+2n 3+…+(k -1)n k七．证明：(8分) 设G 是具有二分类(X,Y)的偶图，证明(1)G 不含奇圈；（2）若|X |≠|Y |，则G 是非哈密尔顿图。

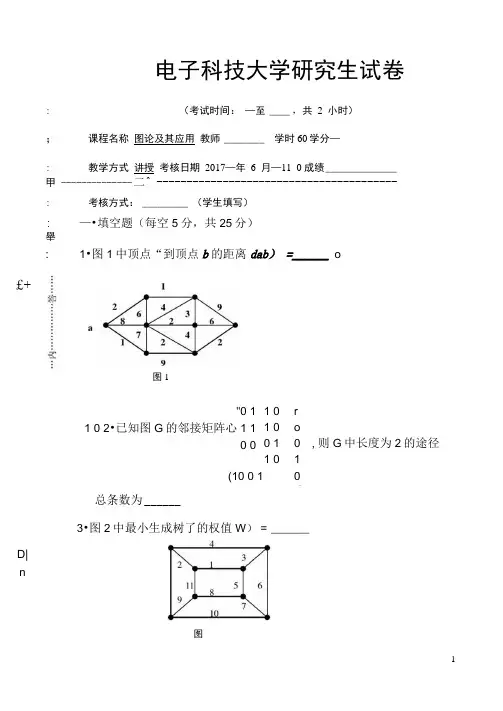
电子科技大学研究生试卷: （考试时间： —至 ____ ，共_2_小时）； 课程名称 图论及其应用 教师 ________ 学时60学分—: 教学方式 讲授 考核日期_2017—年_6_月—11_0 成绩 ______________甲 -------------- 二^ ---------------------------------------- : 考核方式： _________ （学生填写）: —•填空题（每空5分，共25分）舉: 1•图1中顶点“到顶点b 的距离dab ） = ______ o总条数为 ______ 3•图2中最小生成树了的权值W ） = ______£+"0 1 1 0 2•已知图G 的邻接矩阵心1 1 0 0 1 0 1 0 0 1 1 0 (10 0 1 ro0 1丿,则G 中长度为2的途径D|n£+图1图4•图3的最优欧拉环游的权值为5.树叶带权分别为1,245,6,8的最优二元树权值为W(T)=________ 。

二・单项选择(每题3分，共15分)1・关于图的度序列，下列说法正确的是()(A) 对任意一个非负整数序列来说，它都是某图的度序列;(B) 如果非负整数序列K归…心满足「为偶数则它一定是图序/-I列；(C) 若图G度弱于图H ,则图G的边数小于等于图H的边数；(D) .如果图G的顶点总度数大于或等于图H的顶点总度数，则图G度优于图H o2・关于图的割点与割边，下列说法正确的是()(A) 有割边的图一定有割点；(B) 有割点的图一定有割边；(C) 有割边的简单图一定有割点;(D) 割边不在图的任一圈中。

3•设k(G) , 2(G) , 5(G)分别表示图G的点连通度，边连通度和最小度。

下面说法错误的是()(A) 存在图G ,使得狀G)= 5(G) = 2(G)；(B) 存在图G ,使得k(G)<A(G)<3(G)；(C) 设G是n阶简单图，若J(G)> J ,则G连通,且A(G)=J(G);(D) 图G是£连通的，则G的连通度为44•关于哈密尔顿图，下列命题错误的是()(A) 彼得森图是非哈密尔顿图;(B) 若图G的闭包是哈密尔顿图，则其闭包一定是完全图；(C) 若图G的闭包是完全图，则图G是哈密尔顿图；(D) 设G是三阶以上简单图，若G中任意两个不邻接点“与I，,满足,则G是哈密尔顿图。

图论第四次作业答案4.19n*n 方阵中两两不同行不同列的n 个氧元素的集合成为一个对角线，对角线的权指它的n 个元素之和，试求下列矩阵A 的最小权的对角线：458101176574851296661310745798⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ 解答：问题转化为求K 5,5的最佳匹配，用KM 算法：其K5,5的权矩阵是458101176574851296661310745798-----⎛⎫ ⎪----- ⎪ ⎪----- ⎪----- ⎪ ⎪-----⎝⎭，结果是445105810117657812966613745798⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭，权值为30，或581011767481296661310457845579⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭，权值也是30.5.1求n 顶轮的边色数。

解答：1）在n 顶轮G 中，Δ(G)=n-1 χ’(G)≥n-12）现可构造一个n-1的边正常着色如下：用n-1种颜色对与n 顶轮中心顶点 关联的边着色n 顶轮的不与V 0关联的边V k V k+1着色为V k+2V 0的颜色一致,V n-1V 1着色与V 2V 0相同5.2给出二分图正常Δ边着色的算法解答：先构造出Δ次正则二分图，然后逐次求其完备匹配。

PS ：如果直接求其最大匹配并染色，可能得不到正常Δ边着色.见下图：第一次的匹配是红色线条的话，就需要三种颜色，而Δ(G)=2.5.8有7个老师x 1，x 2…x 7，12个班y 1，y 2….y 12，矩阵A 的a ij 号元素是教师x i 对y j 班一周上课的节数，3233136050552424⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭计算一天应分几节课？若每天8节课，需要几间教室？ 解答：Δ(G)=16, ε(G)=48 如果一周上课5天，每天应上()G 5∆⎧⎫⎨⎬⎩⎭= 4节课. 若每天8节课，一周为40节课，需要教室()40G ε⎧⎫⎨⎬⎩⎭=2间. 5.11求证：χ’(G *K 2) =Δ(G*K 2) .证明：根据P 110中图的积定义可知在H=G*K 2中的顶点(v i 1,v j 2)的顶点的度为2*d(v i 1) +1 所以Δ(H)=2*Δ(G )+1，所以题目等价于证明χ’(G *K 2) =2*Δ(G )+1根据Vizing 定理，χ’(G) ∈ {Δ(G),Δ(G)+1}假设χ’(G)=Δ(G)，构造一个2*Δ(G )+1边正常着色。

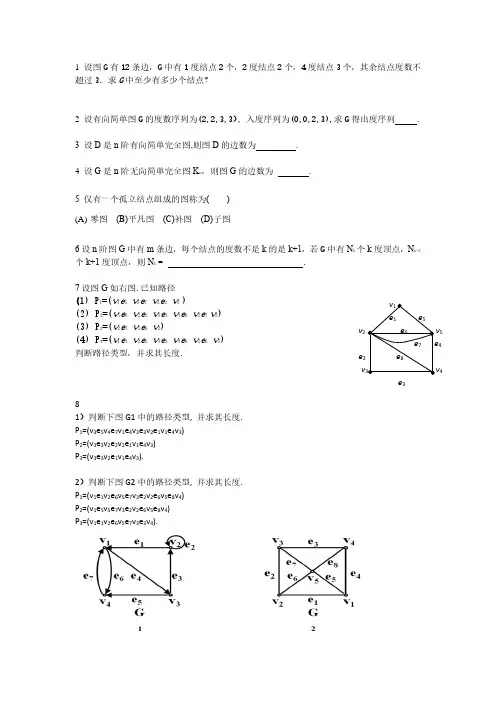
1 设图G有12条边，G中有1度结点2个，2度结点2个，4度结点3个，其余结点度数不超过3．求G中至少有多少个结点？2 设有向简单图G的度数序列为(2,2,3,3）, 入度序列为(0,0,2,3),求G得出度序列 .3 设D是n阶有向简单完全图,则图D的边数为 .4设G是n阶无向简单完全图K n，则图G的边数为 .5 仅有一个孤立结点组成的图称为( )(A)零图(B)平凡图(C)补图(D)子图6设n阶图G中有m条边，每个结点的度数不是k的是k+1，若G中有N k个k度顶点，N k+1个k+1度顶点，则N k = .7设图G如右图.已知路径(1) P1=(v1e5 v5e7 v2e2 v3 )(2) P2=(v5e6 v2e2 v3e3 v4e8 v2e7 v5)(3) P3=(v2e7 v5e6 v2)(4) P4=(v1e1 v2e2 v3e3 v4e8 v2e6 v5)判断路径类型，并求其长度.81）判断下图G1中的路径类型, 并求其长度. P1=(v3e5v4e7v1e4v3e3v2e1v1e4v3)P2=(v3e3v2e2v2e1v1e4v3)P3=(v3e3v2e1v1e4v3).2）判断下图G2中的路径类型, 并求其长度. P1=(v1e1v2e6v5e7v3e2v2e6v5e8v4)P2=(v1e5v5e7v3e2v2e6v5e8v4)P3=(v1e1v2e6v5e7v3e3v4).v1e1e5v2e65e7e4 e2e8v3 4e3v e v1 设图G 有12条边，G 中有1度结点2个，2度结点2个，4度结点3个，其余结点度数不超过3．求G 中至少有多少个结点？ 至少9个2 设有向简单图G 的度数序列为(2,2,3,3）, 入度序列为(0,0,2,3),求G 得出度序列 （2,2,5,6） .3 设D 是n 阶有向简单完全图,则图D 的边数为 )1(−n n .4 设G 是n 阶无向简单完全图K n ，则图G 的边数为 m =n (n -1)/2 .5 仅有一个孤立结点组成的图称为( B ) (A) 零图 (B)平凡图 (C)补图 (D)子图6设n 阶图G 中有m 条边，每个结点的度数不是k 的是k+1，若G 中有N k 个k 度顶点，N k+1个k+1度顶点，则N k = N k =(k+1)n-2m . 7设图G 如右图.已知路径 (1) P 1=(v 1e 5 v 5e 7 v 2e 2 v 3 ) (2) P 2=(v 5e 6 v 2e 2 v 3e 3 v 4e 8 v 2e 7 v 5) (3) P 3=(v 2e 7 v 5e 6 v 2)(4) P 4=(v 1e 1 v 2e 2 v 3e 3 v 4e 8 v 2e 6 v 5)判断路径类型，并求其长度. (1) 初级通路；3 (2) 简单回路；5 (3) 初级回路；2 (4) 简单通路. 5 81）判断下图G1中的路径类型, 并求其长度. P 1=(v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3) P 2=(v 3e 3v 2e 2v 2e 1v 1e 4v 3) P 3=(v 3e 3v 2e 1v 1e 4v 3).2）判断下图G2中的路径类型, 并求其长度. P 1=(v 1e 1v 2e 6v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 2=(v 1e 5v 5e 7v 3e 2v 2e 6v 5e 8v 4) P 3=(v 1e 1v 2e 6v 5e 7v 3e 3v 4).解：在图G 1中，v 3e 5v 4e 7v 1e 4v 3e 3v 2e 1v 1e 4v 3是一条长度为6的回路，但既不是简单回路，也不是初级回路； v 3e 3v 2e 2v 2e 1v 1e 4v 3是一条长度为4的简单回路，但不是初级回路； v 3e 3v 2e 1v 1e 4v 3是一条长度为3的初级回路。

一、选择题1．若222494x y z ++=，则3x y z ++的最大值（ ）A ．9B ．3C ．1D ．62．若正实数a b c 、、满足22ab bc ac a ++=-，则2a b c ++的最小值为（ ） A ．2B ．1C ．2D ．223．设,,,,,a b c A B C R ∈，且满足,a b c A B C ≤≤≤≤，若1S Aa Bb Cc =++，2S Ac Bb Ca =++，3S Ab Bc Ca =++，则 （ ）A ．123S S S ≤≤B ．321S S S ≤≤C ．132S S S ≤≤D ．231S S S ≤≤4．函数526y x x =-+- 的最大值是( )A ．3B ．5C ．3D ．55．已知三个正实数a 、b 、c 满足1a b c ++=，给出以下几个结论：①22213a b c ++≤；②13ab bc ca ++≤；③2221b c a a b c++≥；④3a b c ++≥.则正确的结论个数为( ) A ．1B ．2C ．3D ．46．已知12,F F 是椭圆和双曲线的公共焦点，P 是它们的一个公共点，且123F PF π∠= ，记椭圆和双曲线的离心率分别为12,e e ，则1213e e +的最大值为（ ） A ．223B ．233C ．23D ．227．若222x 4y 9z 4++=，则x y+3z +的最大值（ ） A ．9B ．3C ．1D ．278．已知空间向量(1,0,0),(1,1,0),(0,0,1),OA OB OC === 向量,OP xOA yOB zOC =++且424x y z ++=,则OP 不可能是 A ．12B ．1C ．32D ．49．若5x 1+6x 2-7x 3+4x 4=1,则222212343x 2x 5x x +++的最小值是（ ） A ．78215B ．15782C ．3D ．25310．设a 、b 、c 、x 、y 、z 是正数，且22210a b c ＋＋＝，22240x y z ＋＋＝，20ax by cz ＋＋＝，则＝( )A ．B ．C ．D ．11．已知,,(0,1)a b c ∈，且1ab bc ac ++=，则111111a b c++---的最小值为（ ） A ．332- B ．932- C ．632- D ．9332+ 12．已知函数1212)(+=x x －x f ，则不等式12log (1)(2)f x f x ⎛⎫-+- ⎪⎝⎭＞0的解集为（ ） A ．（2，3） B ．（1，3） C ．（0，2） D ．（1，2）二、填空题13．已知a ，b ，c 均为非负数，且494a b c ++=，则111111a b c +++++的最小值为______．14．设函数()221f x x x =--+的最大值为m . （1）求m 的值；（2）若a b m +=，求124a b +++的最大值. 15．已知,,x y z 是正数，且1231x y z ++=，则23y zx ++的最小值是__________. 16．函数2121y x x =-++的最大值为______. 17．三棱锥的四个顶点都在半径为4的球面上，且三条侧棱两两互相垂直，则该三棱锥侧面积的最大值为________________.18．若正数,,a b c 满足41a b c ++=,2a b c _________ 19．求函数y ＝1102x x --20．已知实数x y 、、z 满足231x y z ++=，则222x y z ++的最小值为 .三、解答题21．若a ，b ，c ∈R ＋，且满足a ＋b ＋c ＝2. （1）求abc 的最大值； （2）证明：11192a b c ++≥. 22．已知不等式2315x x -++≤的解集为[],a b ． （Ⅰ）求+a b 的值；（Ⅱ）若0x >，0y >，40bx y a ++=，求证：9x y xy +≥. 23．已知a ，b ，c 为正实数，且a+b+c=1. （Ⅰ）证明：1111118a b c ⎛⎫⎛⎫⎛⎫---≥⎪⎪⎪⎝⎭⎝⎭⎝⎭；（Ⅱ）证明：32++≥+++a b c b c a c a b . 24．已知函数f （x ）＝|x +1|﹣|2x ﹣2|的最大值为M ，正实数a ，b 满足a +b ＝M ． （1）求2a 2+b 2的最小值； （2）求证：a a b b ≥ab ．25．已知x ，y ，z 均是正实数，且2229436x y z ++=，求证7x y z ++≤． 26．已知正实数a 、b 、c 满足3a b c ++≤，求证11131112a b c ++≥+++.【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】利用条件构造柯西不等式()22222221(3)49112x y z x y z ⎛⎤⎛⎫++≤++++ ⎥ ⎪ ⎝⎭⎥⎝⎦即可 【详解】解：由题得()()()()22222221231132x y z x y z ⎡⎤⎛⎫⎡⎤++++≥++⎢⎥ ⎪⎣⎦⎝⎭⎢⎥⎣⎦，所以()29434x y z ⨯≥++，所以333x y z -≤++≤， 所以3x y z ++的最大值为3 故选：B. 【点睛】考查柯西不等式求最值，基础题.2．D解析：D 【解析】分析：根据基本不等式的性质求出2a+b+c 的最小值即可． 详解：由题得：因为a 2+ac+ab+bc=2， ∴（a+b ）（a+c ）=2，又a ，b ，c 均为正实数，∴2a+b+c=（a+b ）+（a+c ）当且仅当a+b=a+c 时，即b=c 取等号． 故选D.点睛：本题考查了绝对值的意义，考查基本不等式的性质，是一道基础题．3．D解析：D 【分析】由排序不等式可直接得解. 【详解】,a b c A B C ≤≤≤≤，1S Aa Bb Cc =++为顺序和，2S Ac Bb Ca =++为倒序和，3S Ab Bc Ca =++为乱序和，由排序不等式可知：倒序和≤乱序和≤顺序和， 所以231S S S ≤≤. 故选：D. 【点睛】本题主要考查了利用排序不等式比较大小，属于基础题.4．B解析：B 【分析】利用柯西不等式求解. 【详解】因为y ===，即265x =时，取等号.故选：B 【点睛】本题主要考查柯西不等式的应用，还考查了转化化归的思想和运算求解的能力，属于基础题.5．B解析：B 【分析】利用基本不等式及柯西不等式计算可得； 【详解】解：①：222222222a b abb c bc a c ac ⎧+⎪+⎨⎪+⎩，222a b c ab bc ac ∴++++ 2222222()2223()a b c a b c ab ac bc a b c ∴++=+++++++．22213a b c ∴++，故①不正确． ②：由2222()2()3()a b c a b c ab bc ac ab bc ac ++=+++++++，13ab bc ca ∴++，故②正确．③：222222b a b ac b c ba c c c⎧+⎪⎪⎪+⎨⎪⎪+⎪⎩，∴2221b c a a b c a b c ++++=∴2221b c a a b c++，故③正确． ④：由柯西不等式得2()(111)()a b c a b c ++++++，∴3a b c ++≤．则④错误．故选：B ． 【点睛】本题考查利用基本不等式即柯西不等式证明不等式，属于中档题．6．D解析：D 【分析】先设椭圆的长半轴长为1a ,双曲线的半实轴长为2a ,不妨设点P 在第一象限,然后根据椭圆和双曲线的定义可得12||,||PF PF ,再利用余弦定理列等式,转化为离心率的等式后,根据柯西不等式可求得. 【详解】 如图所示:设椭圆的长半轴长为1a ,双曲线的半实轴长为2a ,不妨设点P 在第一象限,则根据椭圆及双曲线的定义得,121||||2PF PF a += ,122||||2PF PF a -=,所以,112||PF a a =+, 212||PF a a =-,设12||2F F c =,123F PF π∠=,则在△1212PF F 中,由余弦定理得2221212121214()()2()()2c a a a a a a a a =++--+-⨯, 即2221243=+c a a ,所以222212134c c a a =+,即2212134e e +=,由柯西不等式得2222212121313(11)(11)([()()]e e e e ⨯+⨯≤++, 即12132422e e +≤⨯=.当且仅当121113e e =,即122e =,262e =时,等号成立.故选:D 【点睛】,本题考查了椭圆和双曲线的定义,余弦定理,离心率,柯西不等式,属于中档题.7．B解析：B 【分析】利用柯西不等式22222221[()2)(3)][1()1](3)2x y z x y z ++++≥++（求解. 【详解】由题得22222221[()2)(3)][1()1](3)2x y z x y z ++++≥++（， 所以2943),4x y z ⋅≥++（ 所以-3≤x+y+3z≤3.所以+3x y z +的最大值为3. 故选B 【点睛】本题主要考查柯西不等式求最值，意在考查学生对这些知识的理解掌握水平和分析推理能力.8．A解析：A 【分析】由题求得OP 的坐标，求得OP ，结合424x y z ++=可得答案. 【详解】(),,x y y z =+ ，(OP x =利用柯西不等式可得()()()22222224214216x y y z x y z ⎡⎤⎡⎤+-++++≥++=⎣⎦⎣⎦ 21621OP ∴≥. 故选A. 【点睛】本题考查空间向量的线性坐标运算及空间向量向量模的求法，属基础题.9．B解析：B 【解析】 【分析】由题意结合柯西不等式的结论整理计算即可求得最终结果. 【详解】由题意结合柯西不等式有：()222212342549325181635x x x x ⎛⎫+++⨯+++ ⎪⎝⎭()212345674x x x x ≥+++()2123456741x x x x ≥+-+=.故2222123415325782x x x x +++≥. 本题选择B 选项. 【点睛】本题主要考查柯西不等式其最值的方法，意在考查学生的转化能力和计算求解能力.10．C解析：C 【解析】由柯西不等式得()2222222111111444222a b c x y z ax by cz ⎛⎫⎛⎫++≥++ ⎪ ⎪⎝⎭⎝⎭＋＋, 当且仅当111222a b cx y z ==时等号成立∵22210a b c ＋＋＝，22240x y z ＋＋＝，20ax by cz ＋＋＝∴()2222222111111444222a b c x y z ax by cz ⎛⎫⎛⎫++≥++ ⎪ ⎪⎝⎭⎝⎭＋＋中等号成立，∴一定有：111222a b c x y z ==，∴12a b c x y z === 则12a b c x y z ++=++ 故选C11．D解析：D 【解析】21110,,1,()3()33,()111a b c a b c ab bc ca a b c a b c<<∴++≥++=∴++≥++---(1a -+11)b c -+-2111111[(1)(1)(1)]9,111111a b c a b c a b c-+-+-=∴++≥------9(111)a b c -+-+-92+≥=D.，故选 【点睛】本题考查柯西不等式，涉及转化化归思想，考查逻辑思维能力、等价转化能力、运算求解能力，综合性较强，属于中档题.本题想用基本不等式公式求得a b c ++≥利用柯西不等式公式求得111()(111)111a b c a b c++-+-+----9,≥从而求得1119111(111)a b c a b c ++≥≥=----+-+- 12．D解析：D 【解析】试题分析：由已知2112()()2112x xxxf x f x -----===-++，所以()f x 是奇函数，又2()121xf x =-+，2xy =是增函数，因此()f x 也是增函数，不等式12log (1)(2)0f x f x ⎛⎫-+-> ⎪⎝⎭可变为12(log (1)(2)(2)f x f x f x ->--=-，而()f x 为增函数，所以12log (1)2x x ->-，在(1,)+∞上，函数12log (1)y x =-是减函数，函数2y x =-是增函数，且2x =时两者相等，因此不等式12log (1)2x x ->-的解为12x <<．故选D ．考点：函数的奇偶性、单调性，解函数不等式．【名师点睛】本题考查函数的奇偶性与单调性．解函数不等式，即使有函数解析式已知的情况下，也不一定要把函数式代入（而且一般不能代入），而是要利用奇偶性化为()()f a f b <的形式，再由单调性化为()a b a b <>或形式，最终不等式12log (1)2x x ->-是不可用代数法来解的，必须借助函数图象，利用函数的性质解题．二、填空题13．2【分析】根据题意得到再由柯西不等式即可求出结果【详解】因为均为非负数且则所以由柯西不等式可得：所以；当且仅当即由解得：即时等号成立故答案为：2【点睛】本题主要考查由柯西不等式求最值熟记柯西不等式即解析：2 【分析】根据题意得到()()()1419118a b c +++++=，再由柯西不等式，即可求出结果. 【详解】因为a ，b ，c 均为非负数，且494a b c ++=，则()()()1419118a b c +++++=， 所以由柯西不等式可得：()()()()21419111123361111a b a b c c ⎛⎫++≥++=⎡⎤ ++++⎪⎣⎦+++⎝+⎭， 所以11136211118a b c ++≥=+++；==12233a b c +=+=+， 由12233494a b c a b c +=+=+⎧⎨++=⎩解得：2120a b c =⎧⎪⎪=⎨⎪=⎪⎩，即12,,02a b c ===时，等号成立. 故答案为：2. 【点睛】本题主要考查由柯西不等式求最值，熟记柯西不等式即可，属于常考题型.14．（1）3；（2）【分析】（1）分段讨论去掉函数的绝对值号即可（2）把转化成然后利用柯西不等式即可【详解】解：（1）函数所以在区间内单调递增在区间内单调递减故的最大值；（2）由柯西不等式得由己知得故所解析：（1）3；（2） 【分析】（1）分段讨论去掉函数的绝对值号即可（21=【详解】解：（1）函数()4,12213,124,2x x f x x x x x x x +≤-⎧⎪=--+=--<<⎨⎪--≥⎩， 所以()f x 在区间(],1-∞-内单调递增，在区间[)1,-+∞内单调递减. 故()f x 的最大值()13m f =-=； （2）由柯西不等式，得1=.由己知3ab +=故所求最大值为1a =，2b =取得）. 【点睛】考查求含两个绝对值号的不等式的最值求法和用柯西不等式求最值，中档题.15．9【分析】首先根据题意利用代1法可得再借助柯西不等式即可得出结论【详解】是正数且当且仅当时取等号的最小值是9故答案为：9【点睛】本题主要考查利用柯西不等式求最小值的问题属于基础题解析：9 【分析】首先根据题意，利用代“1”法，可得1232323y z y z x x x y z ⎛⎫⎛⎫++=++++ ⎪ ⎪⎝⎭⎝⎭，再借助柯西不等式，即可得出结论. 【详解】,,x y z 是正数，且1231x y z++=， 1232323y z y z x x x y z ⎛⎫⎛⎫∴++=++++ ⎪ ⎪⎝⎭⎝⎭2≥ 2(111)=++ 9=，当且仅当3x =，6y =，9z =时取等号，23y zx ∴++的最小值是9.故答案为：9.【点睛】本题主要考查利用柯西不等式求最小值的问题，属于基础题.16．3【分析】化简函数利用柯西不等式即可求解【详解】由题意函数当且仅当取等号即即时取等号所以函数的最大值为3故答案为：3【点睛】本题主要考查了利用柯西不等式求最值问题其中解答中合理变形熟练应用柯西不等式 解析：3【分析】化简函数1y ==.【详解】由题意，函数1y =3≤==1=12242x x -=+，即0x =时取等号， 所以函数的最大值为3．故答案为：3.【点睛】本题主要考查了利用柯西不等式求最值问题，其中解答中合理变形，熟练应用柯西不等式求解是解答的关键，着重考查了推理与运算能力.17．32【解析】试题分析：设三条侧棱长为abc 则三棱锥的侧面积为又因为所以当且仅当时侧面积达到最大值考点：三棱锥球不等式解析：32【解析】试题分析：设三条侧棱长为a ，b ，c ，则22228a b c ++=，三棱锥的侧面积为1()2S ab bc ca =++，又因为222a b c ab bc ca ++≥++，所以164322S ≤⨯=，当且仅当a b c ==时侧面积达到最大值.考点：三棱锥，球，不等式.18．【分析】直接利用柯西不等式列式化简后可求得最大值【详解】由柯西不等式得即即【点睛】本小题主要考查利用利用柯西不等式求最大值考查化归与转化的数学思想方法属于基础题解析：2【分析】直接利用柯西不等式列式，化简后可求得最大值.【详解】由柯西不等式得222222111112⎡⎤⎫⎡⎤⎢⎥++++≥⎪⎢⎥⎣⎦⎢⎥⎭⎝⎭⎣⎦，即()2542a b c++≥2≤.【点睛】本小题主要考查利用利用柯西不等式求最大值，考查化归与转化的数学思想方法，属于基础题.19．【解析】【分析】根据柯西不等式即可求出答案【详解】函数的定义域为15且y＞0y＝56当且仅当时等号成立即时函数取最大值【点睛】本题考查了绝对值不等式的解法和柯西不等式的应用属于基础题解析：【解析】【分析】根据柯西不等式即可求出答案．【详解】函数的定义域为[1，5]，且y＞0，y＝5≤==5=时，等号成立，即12727x=时，函数取最大值【点睛】本题考查了绝对值不等式的解法和柯西不等式的应用，属于基础题．20．【分析】利用条件构造柯西不等式进行解答即可【详解】由柯西不等式可知:即故当且仅当即的最小值为故答案为【点睛】本题主要考查了利用柯西不等式求最值属于中档题利用柯西不等式求最值时关键是对原目标函数进行配解析：114【分析】利用条件231x y z++=,构造柯西不等式()()()222222223123x y z x y z++≤++++，进行解答即可.【详解】由柯西不等式可知:()()()222222223123x y z x y z++≤++++,即()222141x y z++≥故222114x y z++≥,当且仅当123x y z==,即222x y z ++的最小值为114. 故答案为114. 【点睛】本题主要考查了利用柯西不等式求最值,属于中档题.利用柯西不等式求最值时， 关键是对原目标函数进行配凑，以保证出现常数结果.同时，要注意等号成立的条件, 配凑过程采取如下方法：一是考虑题设条件；二是对原目标函数进行配凑后利用柯西不等式解答.三、解答题21．（1）827；（2）证明见解析. 【分析】（1）直接利用三个数的基本不等式求最值即可；（2）将a ＋b ＋c ＝2代入，利用柯西不等式证明即可.【详解】(1)因为a ，b ，c ∈R ＋，所以2＝a ＋b ＋c ≥827abc ≥，故827abc ≤. 当且仅当a ＝b ＝c ＝23时等号成立，所以abc 的最大值为827； (2)证明：因为a ，b ，c ∈R ＋，且a ＋b ＋c ＝2，所以根据柯西不等式， 可得111a b c ++＝12 (a ＋b ＋c ) 111a b c ⎛⎫++ ⎪⎝⎭＝22222212⎡⎤⎢⎥++⎢⎥⎡⎤⎣⎣+⎢⎥⎦+⎦ 21922≥=，当且仅当23a b c ===时等号成立. 所以11192a b c ++≥. 【点睛】 本题的解题关键是利用已知条件拼凑111a b c ++＝12 (a ＋b ＋c ) 111a b c ⎛⎫++ ⎪⎝⎭，观察使用柯西不等式求最值，突破难点即可.22．（Ⅰ）0；（Ⅱ）证明见解析.【分析】（1）根据13x <-，123x -≤≤，2x >进行分类讨论，求出不等式2315x x -++≤的解集，由此能求出a+b ．（2）由x ＞0，y ＞0，41x y +=，知()11114x y x y xy y x y x ⎛⎫+=+=++ ⎪⎝⎭ 414x y y x=+++，由此利用作商法和基本不等式的性质能证明x +y ≥9xy ． 【详解】（Ⅰ）原不等式等价于13415x x ⎧<-⎪⎨⎪-+≤⎩或123325x x ⎧-≤≤⎪⎨⎪+≤⎩或2415x x >⎧⎨-≤⎩， 解得113x -≤<或113x ≤≤，即11x -≤≤ ∴1a =-，1b =， ∴0a b +=.（Ⅱ）由（Ⅰ）知410x y +-=，即41x y +=，且0x >，0y >， ∴()11114x y x y xy y x y x ⎛⎫+=+=++ ⎪⎝⎭41459x y y x =+++≥=， 当且仅当16x =，13y =时取“=”,∴9x y xy +≥. 【点睛】本题考查含绝对值不等式的解法，考查不等式的证明，考查了基本不等式求最值，运用了推理论证能力、运算求解能力，是中档题．23．（Ⅰ）证明见解析；（Ⅱ）证明见解析.【分析】（Ⅰ）每个式子通分后把1用a b c ++代换后分子应用基本不等式可证结论； （Ⅱ）变形111a b c a b c a b c a b c b c a c a b b c a c a b ++++++⎛⎫⎛⎫⎛⎫++=-+-+- ⎪ ⎪ ⎪++++++⎝⎭⎝⎭⎝⎭，三个分式中分子a b c ++提取出来并变为()()()12b c a c a b ⎡⎤+++++⎣⎦，即原不等式左边 ()()()111132b c a c a b b c a c a b ⎛⎫⎡⎤=+++++++- ⎪⎣⎦+++⎝⎭，再用柯西不等式可证得结论．【详解】证明：（Ⅰ）1111111118a b c b c a c a b a b c a b c a b c ---+++⎛⎫⎛⎫⎛⎫---=⋅⋅=⋅⋅≥= ⎪⎪⎪⎝⎭⎝⎭⎝⎭，当且仅当“a=b=c ”时取等号；（Ⅱ）111a b c a b c a b c a b c b c a c a b b c a c a b ++++++⎛⎫⎛⎫⎛⎫++=-+-+- ⎪ ⎪ ⎪++++++⎝⎭⎝⎭⎝⎭()()()111132b c a c a b b c a c a b ⎛⎫⎡⎤=+++++++- ⎪⎣⎦+++⎝⎭22113333222≥-=⨯-=，当且仅当“a =b =c ”时取等号.【点睛】本题考查用基本不等式和柯西不等式证明不等式成立，解题关键是要凑出基本不等式和柯西不等式的形式，然后才可得出结论，掌握基本不等式和柯西不等式是解题．24．（1）83；（2）详见解析． 【分析】（1）去绝对值得分段函数：3,1()31,113,1x x f x x x x x -≤-⎧⎪=--<<⎨⎪-+≥⎩，由单调性易求函数f （x ）的最大值，即有M 的值，再由柯西不等式，即可得到所求最小值；（2）应用分析法证明，考虑两边取自然对数，结合因式分解和不等式的性质、对数的性质，即可得证.【详解】解：（1）函数3,1()31,113,1x x f x x x x x -≤-⎧⎪=--<<⎨⎪-+≥⎩，∴()f x 在（−∞，1）上单调递增，在（1，＋∞）上单调递减，当x ＝1时，f （x ）取得最大值(1)2f =，即M ＝2，正实数a ，b 满足a +b ＝2，由柯西不等式可得（2a 2+b 2）（12+1）≥b ）2， 化为2a 2+b 22()8332a b +≥=， 所以当2222b a =，即b 43=，a 23=时，2a 2+b 2取得最小值83； （2）证明：因为a +b ＝2，a ，b ＞0，要证a a b b ≥ab ，即证a ln a +b ln b ≥ln a +ln b ， 即证（a ﹣1）ln a ≥（1﹣b ）ln b ，即证（a ﹣1）ln a ≥（a ﹣1）ln （2﹣a ），即证（1﹣a ）ln （2a-1）≥0，当0＜a ＜1时，2a -1＞1，所以ln （2a-1）＞0， 由1﹣a ＞0，可得（1﹣a ）ln （2a -1）＞0； 当a ＝1时，（1﹣a ）ln （2a -1）＝0； 当1＜a ＜2时，02a -＜1＜1，所以ln （2a-1）＜0， 因为1﹣a ＜0，所以（1﹣a ）ln （2a -1）＞0， 综上所述，（1﹣a ）ln （2a-1）≥0成立，即a a b b ≥ab . 【点睛】 本题考查含绝对值的函数最值的求解，考查柯西不等式的应用以及分析法证明不等式，考查学生计算能力与分析能力，是中档题.25．详见解析【分析】根据柯西不等式可得()()()22222221132132x y z x y z ⎡⎤⎛⎫⎛⎫⎡⎤++++≥++⎢⎥ ⎪ ⎪⎣⎦⎝⎭⎝⎭⎢⎥⎣⎦，即可得证. 【详解】证明：由柯西不等式得()()()22222221132132x y z x y z ⎡⎤⎛⎫⎛⎫⎡⎤++++≥++⎢⎥ ⎪ ⎪⎣⎦⎝⎭⎝⎭⎢⎥⎣⎦， 当且仅当94x y x ==时等号成立.因为2229436x y x ++=，所以()249364936x y z ++≤⨯=， 所以7x y z ++≤，【点睛】本题主要考查了利用柯西不等式证明不等式，考查了推理能力，属于中档题.26．见解析【分析】由题意可得(1)(1)(1)6a b c +++++≤，再由柯西不等式可得111[(1)(1)(1)]9111a b c a b c ⎛⎫+++++++≥ ⎪+++⎝⎭，即可得证. 【详解】 证明：3a b c ++≤，∴(1)(1)(1)6a b c +++++≤，由柯西不等式得111[(1)(1)(1)]111a b c a b c ⎛⎫+++++++≥ ⎪+++⎝⎭223=， ∴111993111(1)(1)(1)62a b c a b c ++≥≥=++++++++． 【点睛】本题考查了利用柯西不等式证明不等式，考查了推理能力，属于中档题.。

习题1： 4,5,11,12,17,184．证明 将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-28的两个图是同构的。

5.分析：四个顶点的简单图最少边数为 0，最多边数为 6，所以可按边数进行枚举。

11.证明 由于7个顶点的简单图的最大度不会超过6，因此序列(7,6,5,4,3,3,2)不是图序列；(6,6,5,4,3,3,1)是图序列⇔（5，4，3，2，2，0）是图序列，然（5，4，2，2，0）不是图序列，所以(6,6,5,4,3,3,1) 不是图序列。

12.证明 只就连通图证明即可。

设V(G)=｛v 1,v 2,…,v n ｝,对于G 中的路v 1v 2…v k ,(a)v 1v 2v 3v 4 v 5 v 6v 7v 8 v 9v 10 u 1 u 2 u 3 u 4u 5 u 6u 7 u 8 u 9u 10(b)若v k 与v 1邻接，则构成一个圈。

若v i1v i2…v in 是一条路，由于δ≥ 2，因此，对v in ，存在点v ik 与之邻接，则v ik ⋯v in v ik 构成一个圈 。

17.证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支，显然u 与v 在_G 中连通；若u 与v 属于g 的同一连通分支，设w 为G 的另一个连通分支中的一个顶点，则u 与w ，v 与w 分别在_G 中连通，因此，u 与v 在_G 中连通。

18.证明: 因为e 只能属于G 的某一个连通分支,所以只需考虑G 是连通图的情况. 若G − e 仍然连通,则ω(G) = 1 = ω(G − e) < 2 = ω(G) + 1. 若G − e 不连通,则ω(G) = 1 < 2 = ω(G − e) = ω(G) + 1.习题2: 1,9,161. 证明 设是非平凡树T 中一条最长路，若则与在中的邻接点只能有一个，否则，若与除了中顶点之外的其他顶点相连，则可以继续延长，这与是最长路是相矛盾的。

习题三：● 证明：e 是连通图G 的割边当且仅当V(G)可划分为两个子集V1和V2，使对任意u ∈V 1及v ∈V 2, G 中的路（u ，v ）必含e .证明：充分性: e 是G 的割边，故G −e 至少含有两个连通分支，设V 1是其中一个连通分支的顶点集，V 2是其余分支的顶点集，对12,u V v V ∀∈∀∈，因为G 中的u,v 不连通，而在G 中u 与v 连通，所以e 在每一条(u,v)路上，G 中的(u,v)必含e 。

必要性：取12,u V v V ∈∈，由假设G 中所有(u,v)路均含有边e ，从而在G −e 中不存在从u 与到v 的路，这表明G 不连通，所以e 是割边。

● 3.设G 是阶大于2的连通图，证明下列命题等价：（1） G 是块（2） G 无环且任意一个点和任意一条边都位于同一个圈上；（3） G 无环且任意三个不同点都位于同一条路上。

（1）→（2）：G 是块，任取G 的一点u ，一边e ，在e 边插入一点v ，使得e 成为两条边，由此得到新图G 1，显然G 1的是阶数大于3的块，由定理，G 中的u,v 位于同一个圈上，于是G 1中u 与边e 都位于同一个圈上。

（2）→（3）：G 无环，且任意一点和任意一条边都位于同一个圈上，任取G 的点u ，边e ，若u 在e 上，则三个不同点位于同一个闭路，即位于同一条路，如u 不在e 上，由定理，e 的两点在同一个闭路上，在e 边插入一个点v ，由此得到新图G 1，显然G 1的是阶数大于3的块，则两条边的三个不同点在同一条路上。

（3）→（1）：G 连通，若G 不是块，则G 中存在着割点u ，划分为不同的子集块V 1, V 2, V 1, V 2无环，12,x v y v ∈∈，点u 在每一条(x,y)的路上，则与已知矛盾，G 是块。

●7.证明：若v 是简单图G 的一个割点，则v 不是补图G̅的割点。

证明：v 是单图G 的割点，则G −v 有两个连通分支。

离散数学作业4离散数学图论部分形成性考核书面作业本课程形成性考核书面作业共3次，内容主要分别是集合论部分、图论部分、数理逻辑部分的综合练习，基本上是按照考试的题型（除单项选择题外）安排练习题目，目的是通过综合性书面作业，使同学自己检验学习成果，找出掌握的薄弱知识点，重点复习，争取尽快掌握。

本次形考书面作业是第二次作业，大家要认真及时地完成图论部分的综合练习作业。

一、填空题1．已知图G 中有1个1度结点，2个2度结点，3个3度结点，4个4度结点，则G 的边数是 15 ．2．设给定图G (如右由图所示)，则图G 的点割集是 {f} ．3．设G 是一个图，结点集合为V ，边集合为E ，则G 的结点 度数之和 等于边数的两倍．4．无向图G 存在欧拉回路，当且仅当G 连通且 等于出度 ．5．设G=<V ，E >是具有n 个结点的简单图，若在G 中每一对结点度数之和大于等于 n-1 ，则在G 中存在一条汉密尔顿路．姓 名： 学 号：得 分：6．若图G=<V, E>中具有一条汉密尔顿回路，则对于结点集V的每个非空子集S，在G中删除S中的所有结点得到的连通分支数为W，则S中结点数|S|与W满足的关系式为W(G-V1) V1．有n个结点(n2)，m条边，当n为奇数时，7．设完全图KnK中存在欧拉回路．n8．结点数v与边数e满足e=v-1 关系的无向连通图就是树．9．设图G是有6个结点的连通图，结点的总度数为18，则可从G中删去4 条边后使之变成树．10．设正则5叉树的树叶数为17，则分支数为i = 5 ．二、判断说明题（判断下列各题，并说明理由．）1．如果图G是无向图，且其结点度数均为偶数，则图G存在一条欧拉回路．．(1) 不正确，缺了一个条件，图G应该是连通图，可以找出一个反例，比如图G是一个有孤立结点的图。

2．如下图所示的图G存在一条欧拉回路．(2) 不正确，图中有奇数度结点，所以不存在是欧拉回路。

习题一1. （题14）：证明图1-28中的两图是同构的证明 将图1-28的两图顶点标号为如下的(a)与(b)图作映射f : f(v i )→u i (1≤ i ≤ 10)容易证明，对∀v i v j ∈E((a)),有f(v i v j )=u i u j ∈E((b)) (1≤ i ≤ 10, 1≤j ≤ 10 ) 由图的同构定义知，图1-27的两个图是同构的。

2. （题6）设G 是具有m 条边的n 阶简单图。

证明：m =⎪⎪⎭⎫⎝⎛2n 当且仅当G 是完全图。

证明 必要性 若G 为非完全图，则∃ v ∈V(G),有d(v)< n-1 ⇒ ∑ d(v) < n(n-1) ⇒ 2m <n(n-1)⇒ m < n(n-1)/2=⎪⎪⎭⎫⎝⎛2n , 与已知矛盾！充分性 若G 为完全图，则 2m=∑ d(v) =n(n-1) ⇒ m= ⎪⎪⎭⎫⎝⎛2n 。

3. （题9）证明：若k 正则偶图具有二分类V = V 1∪V 2，则 | V 1| = |V 2|。

图1-28 (a)v 2 v 3u 4u (b)证明 由于G 为k 正则偶图，所以，k | V 1 | =m = k | V 2 | ⇒ ∣V 1∣= ∣V 2 ∣。

4. （题12）证明：若δ≥2，则G 包含圈。

证明 只就连通图证明即可。

设V(G)=｛v 1,v 2,…,v n ｝,对于G 中的路v 1v 2…v k ,若v k 与v 1邻接，则构成一个圈。

若v i1v i2…v in 是一条路，由于δ≥ 2，因此，对v in ，存在点v ik 与之邻接，则v ik ⋯v in v ik 构成一个圈 。

5. （题17）证明：若G 不连通，则G 连通。

证明 对)(,_G V v u ∈∀,若u 与v 属于G 的不同连通分支，显然u 与v 在_G 中连通；若u 与v 属于g 的同一连通分支，设w 为G 的另一个连通分支中的一个顶点，则u 与w ，v 与w 分别在_G 中连通，因此，u 与v 在_G 中连通。

1电子科技大学研究生试卷（考试时间： 至 ，共__2_小时）课程名称 图论及其应用 教师 学时 60 学分 教学方式 讲授 考核日期_2013__年_6__月__20__日 成绩 考核方式： （学生填写）一．填空题(每空2分，共20分)1． n 阶k 正则图G 的边数m =_____。

2．4个顶点的不同构单图的个数为________。

3．完全偶图,r s K (,2r s ≥且为偶数)，则在其欧拉环游中共含____条边。

4．高为h 的完全2元树至少有_______片树叶。

5. G 由3个连通分支124,,K K K 组成的平面图，则其共有_______个面。

6. 设图G 与5K 同胚，则至少从G 中删掉_______条边，才可能使其成为可平面图。

7. 设G 为偶图，其最小点覆盖数为α，则其最大匹配包含的边数为________。

8. 完全图6K 能分解为________个边不重合的一因子之并。

9. 奇圈的边色数为______。

10. 彼得森图的点色数为_______。

二．单项选择(每题3分，共15分) 1．下面说法错误的是( )学 号 姓 名 学 院…………………… 密……………封……………线……………以……………内……………答…… ………题……………无……………效……………………2(A) 图G 中的一个点独立集，在其补图中的点导出子图必为一个完全子图；(B) 若图G 连通，则其补图必连通； (C) 存在5阶的自补图； (D) 4阶图的补图全是可平面图. 2．下列说法错误的是（ ） (A) 非平凡树是偶图；(B) 超立方体图(n 方体,1n ≥)是偶图； (C) 存在完美匹配的圈是偶图； (D) 偶图至少包含一条边。

3.下面说法正确的是( )(A) 2连通图一定没有割点（假定可以有自环）； (B) 没有割点的图一定没有割边；(C) 如果3阶及其以上的图G 是块，则G 中无环，且任意两点均位于同一圈上；(D) 有环的图一定不是块。

5.10 用16K×1位的DRAM芯片组成64K×8位存储器，要求：(1) 画出该存储器的组成逻辑框图。

(2) 设存储器读/写周期为0.5μS, CPU在1μS内至多要访问一次。

试问采用哪种刷新方式比较合理？两次刷新的最大时间间隔是多少？对全部存储单元刷新一遍所需的实际刷新时间是多少？（1）组建存储器共需DRAM芯片数N=（64K*8）/（16K*1）=4*8（片）。

每8片组成16K×8位的存储区，A13~A0作为片内地址，用A15、A14经2:4译码器产生片选信号，逻辑框图如下（图有误：应该每组8片，每片数据线为1根）（2）设16K×8位存储芯片的阵列结构为128行×128列，刷新周期为2ms。

因为刷新每行需0.5μS，则两次（行）刷新的最大时间间隔应小于：为保证在每个1μS内都留出0.5μS给CPU访问内存，因此该DRAM适合采用分散式或异步式刷新方式，而不能采用集中式刷新方式。

●若采用分散刷新方式，则每个存储器读/写周期可视为1μS，前0.5μS用于读写，后0.5μS用于刷新。

相当于每1μS刷新一行，刷完一遍需要128×1μS＝128μS，满足刷新周期小于2ms的要求；●若采用异步刷新方式，则应保证两次刷新的时间间隔小于15.5μS。

如每隔14个读写周期刷新一行，相当于每15μS刷新一行，刷完一遍需要128×15μS＝1920μS，满足刷新周期小于2ms的要求；需要补充的知识：刷新周期：从上一次对整个存储器刷新结束到下一次对整个存储器全部刷新一遍为止的时间间隔。

刷新周期通常可以是2ms，4ms或8ms。

DRAM一般是按行刷新，常用的刷新方式包括：●集中式：正常读/写操作与刷新操作分开进行，刷新集中完成。

特点：存在一段停止读/写操作的死时间，适用于高速存储器。

（DRAM 共128行，刷新周期为2ms ，读/写/刷新时间均为0.5μS ）● 分散式：一个存储系统周期分成两个时间片，分时进行正常读/写操作和刷新操作。