人教课标版2018年元旦八年级数学竞赛题

2018年全国初中数学联合竞赛试题(含解答)2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准。

第一试，选择题和填空题只设7分和0分两档；第二试各题，请严格按照本评分标准规定的评分档次给分，不要再增加其他中间档次。

如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数。

第一试一、选择题（本题满分42分，每小题7分）1.已知$x,y,z$满足$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$，则$\frac{y+2z}{3x-y-z}$的值为（）A) 1.(B) $\frac{5}{3}$。

(C) $-\frac{1}{3}$。

(D) $-\frac{3}{5}$.答】B.解：由$\frac{2355x-y}{y+2z}=\frac{x}{z-z^2}$，得$5x-3y=3xz-3xz^2$，即$y=\frac{5}{3}x-\frac{3}{3}z+\frac{3}{3}xz^2$，所以$\frac{y+2z}{3x-y-z}=\frac{\frac{5}{3}x+\frac{1}{3}z}{\frac{4}{3}x-\frac{2}{3}z}=\frac{5}{3}$，故选（B）。

注：本题也可用特殊值法来判断。

2.当$x$分别取值$1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{2006}, \frac{1}{2007}$时，计算$\frac{1}{2007}+\frac{x}{21+x^2}$代数式的值，将所得的结果相加，其和等于（）A) $-1$。

(B) $1$。

(C) $0$。

(D) $2007$.答】C.解：$\frac{1}{2007}+\frac{x}{21+x^2}=\frac{1}{21}\left(\frac{21}{ 2007}+\frac{21x}{21+x^2}\right)=\frac{1}{21}\left(\frac{1}{1+x ^{-2}}\right)$，所以当$x=1,\frac{1}{2},\frac{1}{3},\cdots,\frac{1}{2005},\frac{1}{200 6},\frac{1}{2007}$时，计算所得的代数式的值之和为$0$，故选（C）。

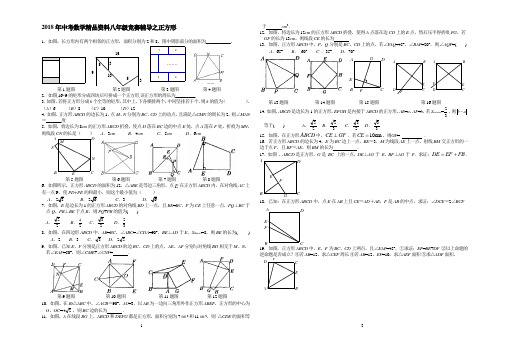
2018年中考数学精品资料八年级竞赛辅导之正方形1．如图，长方形内有两个相邻的正方形，面积分别为2和8，图中阴影部分的面积为___________。

953351016第7题⋅⋅⋅⋅⋅⋅⋅4321第1题图第2题图第3题图第4题图2．如图,16×9的矩形分成四块后可拼成一个正方形,该正方形的周长为_________.3．如图，若将正方形分成k个全等的矩形，其中上、下各横排两个，中间坚排若干个，则k的值为（）。

（A）6 （B）8 （C）10 （D）124．如图，正方形ABCD的边长为1，点M、N分别为BC、CD上的动点，且满足△CMN的周长为2，则∠MAN＝_______度.5．如图，将边长为8cm的正方形ABCD折叠，使点D落在BC边的中点E处，点A落在F处，折痕为MN，则线段CN的长是（）A．3cm B．4cm C．5cm D．6cmNMFEDCBA第5题图第6题图第7题图第8题图6．如图所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为（）A．23B．26C．3 D．67．如图，E是边长为1的正方形ABCD的对角线BD上一点，且BE=BC，P为CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R，则PQ+PR的值为( )A．22B．21C．23D．328．如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于E，S ABCD=8，则BE的长为( )A．2 B．3 C．3D．229．如图，已知E、F分别是正方形ABCD的边BC、CD上的点，AE、AF分别与对角线BD相交于M、N，若∠EAF=50°，则∠CME+∠CNF= ．第9题图第10题图第11题图第12题图10．如图，在Rt△ABC中，∠ACB＝90°，AC=3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，OC=24，则BC边的长为．11．如图，A在线段BG上，ABCD和DEFG都是正方形，面积分别为7㎝2和11㎝2，则△CDE的面积等于cm2．12．如图，将边长为12cm的正方形ABCD折叠，使得A点落在边CD上的E点，然后压平得折痕FG，若GF的长为13cm，则线段CE的长为．13．如图，正方形ABCD中，P、Q分别是BC、CD上的点，若∠P AQ=45°，∠BAP=20°，则∠AQP=( )A．65°B．60°C．35°D．70°AB CDEFGF ED CBAA BCDEF第13题图第14题图第15题图第16题图14．如图，ABCD是边长为1的正方形，EFGH是内接于ABCD的正方形，AE=a，AF=b，若S EFGH=32，则ab-等于( ) A．22B．32C．23D．3315．如图，在正方形ABCD中，C E G F⊥．若10cmCE=，则GF= ．16．若正方形ABCD的边长为4，E为BC边上一点，BE＝3，M为线段AE上一点，射线BM交正方形的一边于点F，且BF＝AE，则BM的长为．17．如图，ABCD是正方形．G是BC 上的一点，DE⊥AG于E，BF⊥AG于F．求证：DE EF FB=+．18．已知：在正方形ABCD中，点E在AB上且CE＝AD＋AE，F是AB的中点，求证：∠DCE＝2∠BCF.FEDCBA19．如图，正方形ABCD中，E、F为BC、CD上两点，且∠EAF=45°，①求证：EF=BE+DF. ②以上命题的逆命题是否成立？③若AB=12，求△CEF周长.④若AB=12，EF=10，求△AEF面积.⑤求△ADF面积.D CBAFEA DEFCB20．如图，BF平行于正方形ADCD的对角线AC，点E在BF上，且AE=AC，CF∥AE，求∠BCF.A CDEF21．如图，ABCD是正方形，AB=1，∠AOx＝30°，求点B坐标.22．数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．90AEF∠=，且EF交正方形外角∠DCG的平行线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证AME ECF△≌△，所以AE=EF．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．23．如图，分别以△ABC的三边向形外作正方形ABDE、BCFG、ACMN，直线OP⊥AB，①求证：OP平分FM；②以上命题的逆命题成立吗？为什么？PONMGFE DCBA24．已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（均不要求证明）25．如图，正方形ABCD被两条与边平行的线段EF、GH分割成4个小矩形，P是EF与GH的交点，若矩形PFCH的面积恰是矩形AGPE面积的2倍，试确定∠HAF的大小，并证明你的结论．A DFC GEB图1 A DFC GEB图2A DFEB图3DE图②图③D图①。

2018年北京市中学⽣数学竞赛初⼆年级竞赛试题试卷编号：21262018年北京市中学⽣数学竞赛初⼆年级竞赛试题⼀、选择题共5⼩题。

在每⼩题列出的四个选项中，选出符合题⽬要求的⼀项。

1.已知√x +1√x=3,则x x 2+2018x +1的值是( )(A)2020(B)12020(C)2025(D)120252.在⾮等腰三⾓形中,⼀个内⾓等于另两个内⾓的差,且⼀个内⾓是另⼀个内⾓的2倍.⼰知该三⾓形的最⼩边长等于l cm,则这个三⾓形的⾯积是( )(A)1cm 2(B)√32cm 2(C)√52cm 2(D)2cm 23.n 是偶数,若从1开始,前n 个正整数的和的尾数是数字8,则后继的n 个正整数的和的尾数是数字( )(A)6(B)4(C)2(D)04.如图,P (xP ,y P )为反⽐例函数y =2x在平⾯直⾓坐标系xOy 的第⼀象限图象上⼀点,过点P 作x 轴、y 轴的平⾏线分别交y =10x 在第⼀象限的图象于点A 和B ,则△AOB 的⾯积等于( )(A)26(B)24(C)22(D)205.将数字和为11的⾃然数按由⼩到⼤的顺序排成⼀个数串,第m 个数是2018,则m 是( )(A)134(B)143(C)341(D)413⼆、填空题共5⼩题。

6.295的约数中⼤于1000000的共有＿＿＿＿＿个.7.若x ,y 都是⾃然数,关于x ,y 的⽅程[2.018x ]+[5.13y ]=24的解(x ,y )共有＿＿＿＿＿个.(其中[x ]表⽰不⼤于x 的最⼤整数)8.D为锐⾓△ABC内⼀点,满⾜AD=DC,∠ADC=2∠DBC,AB=12,BC=10,如图,则△BDC的⾯积等于＿＿＿＿＿.9.已知x1,x2,···,x n中每⼀个x i(i=1,2,···,n)的数值只能取?2,0,l中的⼀个,且满⾜x1+x2+···+x n=?17,x21+x22+···+x2n=37.则(x31+x32+···+x3n)2的值为＿＿＿＿＿.10.在1～n这n个正整数中,正约数个数最多的那些数叫做这n个正整数中的“旺数”,⽐如,正整数1～20中,正约数个数最多的数是l2,18,20,所以12,18,20都是正整数1～20中的“旺数”.在正整数1～100中的所有“旺数”的最⼩公倍数是＿＿＿＿＿.三、解答题共3⼩题。

2017学年第二学期八年级区域数学竞赛试卷（满分120分，时间120分钟）一、选择题（每小题 4分，共32分•在每题给出的四个选项中，只有一个是正确的）1.在平面直角坐标系中，点 P （m,2m -2），则点P 不可能在（ B ） A.第一象限B.第二象限C.第三象限D.第四象限x = m 一 y =2x -2y=2m-22n 半人2.满足n -n -1 =1的整数门有（D ）个.B . 2C . 3D . 42 2n 「n 「1=1—； n 「n 「2=0—； m = 2,n 2 二-12 2n -n -1 二-1—； n -n =0—； n = 0 n 2=0—； n = —23.不等式a — J ： >0的解是（ B ）C. a 1 或 一1 ：： a ：： 0D. a 0 或 a ：： -14.如图，在平行四边形 ABCD 中，AB = 8 cm, AD = 12 cm.点P 在AD 边上以每秒 1 cm 的速度从点A向点D 运动，点Q 在BC 边上，以每秒4 cm 的速度从点C 出发，在CB 间往返运动，两个点同时出发，当点P 达到点D 时停止（同时点 Q 也停止）.在运动过程中，以P , D , Q , B 四点为顶点组成平行四边形的次数有当点P 到达点D 时，Q 运动48cm ，即来回4次，当 0 ：：t 乞3时，不存在；当 3 26》12-t =4t -12 > t = 4.8 ;l a2 . 「.0—； a 1—； a 1 或a TB. a 1 或 a 、1A. 4次B . 3次C . 2次第4题图D . 1次当6 ：t 乞9》12-t =36 -4t > t =8当9 ：t <12》12 -t =4t -36》t = 9.65.如图，在四边形 ABCD 中，AC 丄BD 于点E , BD 〃x 轴，点C 在x 轴上，点 A , D 在12(x 0)的图象上.若L ABE 与L CDE 的面积之比为1 : 3,则L ABC 的面 xA )4a 2-9a -2企=12a -4 -9a -2 —1 +a3a=3a 3 _6 =3（a 〔）_6 =9 _6 =3a a7.如图，矩形ABCD 的长为 a ，宽为b ， 如果1S, = S 2（S 3 S 4），则 S 4 =（ C ） 22 ,3 , 3 ,1 , A. abB. abC. abD. ab3 4 82函数yA. 3B. 5C. 3 51 aD. 6 5积为(A. 2B.C. 3D.43x _1 7 5 + 2x 28.实数x 满足 --------- -一 K x - ------------- ，并且关于 x 的函数 y = 2x-a+a 的最小值为 4,233则常数a= ( C )A. _2B. 1 _ 3C. 2 或 1 - - 3D. -2 或 133x -1 7 5 2x , xx 1233a>1x=1时，y 最小值=4 x=a 时，y 最小值=421-a+a 2=4 a 2=4 2a -2a+2=4a=2a=1-"j 3二、填空题(每小题5分，共30分)9 计算. 一1 -------- + ---------- 1 ------- +川 + -------- — ------- = ______________2+J 2 2 J 3+3^/2 11山2+12丁1111 3+ 21 12 3+3 2= 6( 3+ 2)= 6 = 2- 310.如图，在矩形 OABC 中，A （ 0，2），C （4，0），点M 是直线y = X 上的点，点 N 是 坐标平面内一点. 若四边形MBNC 是平行四边形，则当MN 取最小值时，点N 的坐原式=1-丄+丄-丄+“-+ 屯2屮2 #31 ___ 1 11- 12标是aS i +S 2=S 3+S 42 2 2 8 1 13 S 4=2ab-jab=8ab112.如果 f(4) =4, f 4(39) = 27, f (206) =12,那么5f (1) + f (2) + f(3) +f(4)十…+f(99) + f(100) = _________2116 ____仔细观察式子得到，11 1 -N (T ，-2)11.如图，在平面直角坐标系中, 点C(x, y)是动点,以点C 为旋转中心，将点A(-4,0)逆 时针旋转90°到点B(t,4)，若 -2<t<2，则点C 运动的路径长为 ______ . 22 ____CD=AE — 4-y=-4-x — y=x+8点C 的轨迹是直线：y=x+810 12 14 16 18 20 22原式=(1 + 2 + 3+ - + 8+ 9) + ( 1 + 1 + 2+ 3 +…8+ 9) + ( 2 + 2+ 4 + 6+ - + 16+ 18) + ( 3+ 3 + 6+ 9+ …+ 24+ 27) + …+ (9 + 9+ 18+ 27 + 36+ …+ 72+ 81) = 45X 1 + 46X1 + 46X2+ 46X3 + …+46X8+ 46X9= 45X 1 + 46 >45 = 46X46= 2116.3 2 213.已知a 为常数，关于x 的方程x ・（2a-a ）x-2a =0在实数范围内只有一个解， 则a 的取值为 _______ 0乞a ::: 8 _____［解析］（龙+ 2V — 2工也一工弓=0 + ［（工+ 2）痺十丈叮（总一x ） = 0. 分情况讨论；① 若畑+2加+云=0无解*则△=冷一备＜0“解得0＜血＜恥② 若三根同为将T=a 代人X 1 4-（T + 2）a = 0T 解得d = 0 适合,ABC 中，.C =90，L ABC 内取一点 P ,15.已知实系数一元二次方程ax 2■ 2bx c = 0的两根为X i ,血，若a b c ,且a +b +c = 0 ,求d = x , —x 2的取值范围.14.如图，在等腰直角三角形且 AP = AC =a, BP =CP =b(b :：: a)，则2 ,2a b —72 =a -b补齐正方形ACBD T PBD PCA T 正 PAD T 乙PAC=301 PAC =：a1 1 1 _____________ -a 2=-b? a 2-~b 2T a 2=b 4a 2-b2 4 2 4 T a 4-4a 2b 2+b 4=0 (a 2+b 2)2=6a 2b 2 (a 2-b 2)2=2a 2b 2a 2+b 2 齐=3三、解答题（第 15题13分，15分，共58分）b解：ax 2+2bx+c=0f x i +X 2=-b , a d=X i -X 2= (X I +X 2)2-4X I ?X 2----a>b>c , a+b+c=0cf a>-a-c f2a>-c^ _ >-2 ac 1-a-c>c f -a>2c f 一 <-：--- a 2c 1 -2< <<： ------------ 11 分a 23<d<2 3 ----------- 13 分16.如图，在矩形 ABCO 中，点O 为坐标原点，点 B 的坐标为（4, 3）,点A , C 在坐标轴上，点 P 在BC 边上，直线h ： y =：2x • 3，直线I? ： y =2x -3 . （1）分别求直线l 1与x 轴，直线l 2与AB 的交点坐标；（2） 已知点M 在第一象限，且是直线I ?上的点，若?APM 是等腰直角三角形， 求点M 的(3) 坐标. 已知矩形ANPQ 的顶点N 在直线l 2 上. Q 是坐标平面内的点, 请直接写出x 取值范围.解t O)t (3P 3>. （即①若点A 为直角顶点时、点M 在第一象限，连接AC t 如图 ltZAPB>Z^C^>45\AAAPM 不可能为聘蹬直角三角形’ 二点M 不存在” ---4 分②若点P 为宜瀚顶点时"点M 在第一象限，如图氛 过点M 作MN±CB t 交CB 的延悅线于点N. 则RtAABP^RtAPNMi AAB=FN=4t MN=BP,MN=z —莒2x^-3 = 44-3一 （x 一4）»工二普…山（閉’罟），----7 分cx i ?(2= ------ 2 分a-------------- 4分--8分 10分=企竺=2啤二？ a a 2345③若点M 为直角顶点，点M 在第一象限， 如图3.设 Mi (x*2x^3? T过虑Mi 作MG 丄0A 于点G .交BC 于点 则RtAAMLG^RtAPMj H,・ *.AGi =Mi Hi =3 — •J H +3 — (2X — 3) = 4 *:* 工=2、AM] (2 J}.设Mf （工*2工一3） 9 同理可得工一3 = 4. ・一1° 一工=—I 嫁上所述，点M 的坐椽可以为（普普力⑵普吉 13 分 （3）x 的取值范围为： 15分N 在直线 12 上，N(x, 2x-3)2x-6 2x-6 k AN *BN =-1 T? =-1x x-42 18T 5x -28x+36=0 T X 1= , x 2=2 52x-6 _?x-3k AN *CN =-1 T ? =-1x x-4 11- 31 11+ 31 —,x2=^~ 点P 从C T B 时 T 5x 2-22x+佃=0 5 N 在直线12上,N 在AB 上方, 11+ 31 18$w — 5 5N 在直线12上 ,N 在AB 下方, 11- 31 5 8 810---10 分E , F分别是边BC , CD上的点，满足EF = BE • DF ,17.如图，在正方形ABCD中,AE, AF分别与对角线BD交于点M,N .(1) 求证：①.EAF =45 ;② MN $ 二BM 2DN 2(2) 求兰的最小值AB(1)①延长CB到G,使BG=DF 可得ABG 三ADFf AEG 三AEF f /EAG= EEAF=45° 5 分②在AG取点H，使AH=AN 仝ABH 兰ADN f 厶AMH Z1AMN_BMH 中HM=MN, BH=DN NMBH=45 +45 °90 °MN 2=BM 2+DN2 ------------- 10 分(2)设：AB=a, EF=b, BE=x Rt CEF 中2 2 2CE2+CF 2=EF22 2 2f (a-x) +(a-b+x) =b2 2f x -bx+a -ab=0BE存在，方程有解f—爼)—=b2-4(a2-ab)为b bb2-4a2+4ab 丸f (；)2+4(；)羽b 2 f ( +2)2为ab f 丝2-2-a15分18. 计算机从自然数1 开始由小到大按如下规则进行染色：凡能表示为两个不同合数之和的自然数都染成红色，不符合上述要求的自然数染成黄色(比如29 可表示为两个不同合数20和9之和，29要染红色；1不能表示为两个不同合数之和，1染黄色)。

2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准.第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数.第一试一、选择题：（本题满分42分，每小题7分）1．已知21a ，32b，62c ，那么,,a b c 的大小关系是（）A.ab cB.ac b C.bacD.b ca【答】C. 因为121a，132b，所以110ab，故ba .又(62)(21)6ca(21)，而22(6)(21)3220，所以621，故ca .因此ba c .2．方程222334x xy y的整数解(,)x y 的组数为（）A ．3.B ．4.C ．5.D ．6.【答】B. 方程即22()234xy y，显然x y 必须是偶数，所以可设2x y t ，则原方程变为22217ty，它的整数解为2,3,t y从而可求得原方程的整数解为(,)x y ＝(7,3)，(1,3)，(7,3)，(1,3)，共4组.3．已知正方形ABCD 的边长为1，E 为BC 边的延长线上一点，CE ＝1，连接AE ，与CD 交于点F ，连接BF 并延长与线段DE 交于点G ，则BG 的长为（）A ．63B ．53C ．263D ．253【答】D.过点C 作CP//BG ，交DE 于点P.因为BC ＝CE ＝1，所以CP 是△BEG 的中位线，所以P 为EG 的中点.又因为AD ＝CE ＝1，AD//CE ，所以△ADF ≌△ECF ，所以CF ＝DF ，又CP//FG ，所以FG 是△DCP 的中位线，所以G 为DP 的中点.因此DG ＝GP ＝PE ＝13DE ＝23.连接BD ，易知∠BDC ＝∠EDC ＝45°，所以∠BDE ＝90°. 又BD ＝2，所以BG ＝22225BDDG293.4．已知实数,a b 满足221a b ，则44a ab b 的最小值为（）PGFEBCADA ．18. B ．0. C ．1. D ．98.【答】B.442222222219()2122()48aabbab a bab a b ab ab .因为222||1ab a b ，所以1122ab ，从而311444ab，故2190()416ab，因此219902()488ab，即44908aabb.因此44a abb 的最小值为0，当22,22a b或22,22ab时取得.5．若方程22320x pxp 的两个不相等的实数根12,x x 满足232311224()xxxx ，则实数p的所有可能的值之和为（）A ．0.B ．34. C ．1.D ．54.【答】 B.由一元二次方程的根与系数的关系可得122x x p ，1232x x p ，所以2222121212()2464x x x x x x p p，332212121212()[()3]2(496)xxx x x x x x p pp.又由232311224()x x x x 得223312124()x x x x ，所以2246442(496)p p p pp ，所以(43)(1)0p pp ，所以12330,,14p p p .代入检验可知：1230,4p p 均满足题意，31p 不满足题意. 因此，实数p 的所有可能的值之和为12330()44p p .6．由1，2，3，4这四个数字组成四位数abcd （数字可重复使用），要求满足a cb d .这样的四位数共有（）A ．36个.B ．40个.C ．44个.D ．48个.【答】C.根据使用的不同数字的个数分类考虑：（1）只用1个数字，组成的四位数可以是1111，2222，3333，4444，共有4个.（2）使用2个不同的数字，使用的数字有6种可能（1、2，1、3，1、4，2、3，2、4，3、4）.如果使用的数字是1、2，组成的四位数可以是1122，1221，2112，2211，共有4个；同样地，如果使用的数字是另外5种情况，组成的四位数也各有4个.因此，这样的四位数共有6×4＝24个.（3）使用3个不同的数字，只能是1、2、2、3或2、3、3、4，组成的四位数可以是1232，2123，2321，3212，2343，3234，3432，4323，共有8个.（4）使用4个不同的数字1，2，3，4，组成的四位数可以是1243，1342，2134，2431，3124，3421，4213，4312，共有8个.因此，满足要求的四位数共有4＋24＋8＋8＝44个.二、填空题：（本题满分28分，每小题7分）1．已知互不相等的实数,,a b c 满足111abct b c a，则t_________．【答】1.由1a t b 得1bt a，代入1bt c得11t tac ，整理得2(1)()0ct ac ta c ①又由1c t a 可得1ac at ，代入①式得22()0ctatac ，即2()(1)0c a t，又c a ，所以210t，所以1t.验证可知：11,1a b caa时1t；11,1a bcaa时1t .因此，1t .2．使得521m是完全平方数的整数m 的个数为．【答】1．设2521mn （其中n 为正整数），则2521(1)(1)mnn n ，显然n 为奇数，设21n k （其中k 是正整数），则524(1)mk k ，即252(1)m k k .显然1k，此时k 和1k 互质，所以252,11,m k k 或25,12,m k k 或22,15,m k k 解得5,4k m .因此，满足要求的整数m 只有1个.3．在△ABC 中，已知AB ＝AC ，∠A ＝40°，P 为AB 上一点，∠ACP ＝20°，则BC AP＝．【答】3.设D 为BC 的中点，在△ABC 外作∠CAE ＝20°，则∠BAE ＝60°. 作CE ⊥AE ，PF ⊥AE ，则易证△ACE ≌△ACD ，所以CE ＝CD ＝12BC.又PF ＝PA sin ∠BAE ＝PA sin 60°＝32AP ，PF ＝CE ，所以32AP ＝12BC ，因此BC AP＝3.4．已知实数,,a b c 满足1abc，4a b c ，22243131319a b c aa bb cc ，则222abc ＝．【答】332.因为22313(3)(1)(1)(1)aa aa abc a bc a a bcbc a b c ，所以FEDBCAP2131(1)(1)a aa b c .同理可得2131(1)(1)b b b a c ，2131(1)(1)c cc a b .结合22243131319ab c aa bb cc 可得1114(1)(1)(1)(1)(1)(1)9b c a c a b ，所以4(1)(1)(1)(1)(1)(1)9a b c a b c .结合1abc，4a b c，可得14ab bc ac. 因此，222233()2()2a bca bc ab bc ac .实际上，满足条件的,,a b c 可以分别为11,,422.第二试（A)一、（本题满分20分）已知直角三角形的边长均为整数，周长为30，求它的外接圆的面积.解设直角三角形的三边长分别为,,a b c （a b c ），则30a b c .显然，三角形的外接圆的直径即为斜边长c ，下面先求c 的值.由a b c 及30a b c 得303a b c c ，所以10c . 由a b c 及30a b c 得302a b c c ，所以15c . 又因为c 为整数，所以1114c .……………………5分根据勾股定理可得222abc ，把30ca b 代入，化简得30()4500ab a b ，所以22(30)(30)450235a b ，……………………10分因为,a b 均为整数且a b ，所以只可能是22305,3023,ab解得5,12.a b ……………………15分所以，直角三角形的斜边长13c ，三角形的外接圆的面积为1694.……………………20分二．（本题满分25分）如图，PA 为⊙O 的切线，PBC 为⊙O 的割线，AD ⊥OP 于点D .证明：2ADBD CD .DPOABC2018年全国初中数学联合竞赛试题参考答案及评分标准第1页（共4页）证明：连接OA ，OB ，OC.∵OA ⊥AP ，A D ⊥OP ，∴由射影定理可得2PAPD PO ，2ADPD OD . ……………………5分又由切割线定理可得2PAPB PC ，∴PB PC PD PO ，∴D 、B 、C 、O 四点共圆，……………………10分∴∠PDB ＝∠PCO ＝∠OBC ＝∠ODC ，∠PBD ＝∠COD ，∴△PBD ∽△COD ，……………………20分∴PD BD CD OD，∴2AD PD OD BD CD .……………………25分三．（本题满分25分）已知抛物线216yxbx c 的顶点为P ，与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x （12x x ）两点，与y 轴交于点C ，PA 是△ABC 的外接圆的切线.设M 3(0,)2，若AM//BC ，求抛物线的解析式.解易求得点P 23(3,)2b bc ，点C (0,)c .设△ABC 的外接圆的圆心为D ，则点P 和点D 都在线段AB 的垂直平分线上，设点D 的坐标为(3,)b m .显然，12,x x 是一元二次方程2106x bx c的两根，所以21396x b bc ，22396x bbc ，又AB 的中点E 的坐标为(3,0)b ，所以AE ＝296b c .……………………5分因为PA 为⊙D 的切线，所以PA ⊥AD ，又A E ⊥PD ，所以由射影定理可得2AEPE DE ，即2223(96)()||2bc b c m ，又易知0m，所以可得6m. ……………………10分又由DA ＝DC 得22DA DC ，即22222(96)(30)()bc mb mc ，把6m代入后可解得6c （另一解0c 舍去）.……………………15分又因为AM//BC ，所以OA OM OBOC，即223||3962|6|396b b c bbc.……………………20分把6c 代入解得52b （另一解52b舍去）. 因此，抛物线的解析式为215662y xx . ……………………25分2018年全国初中数学联合竞赛试题参考答案及评分标准第1页（共5页）精品文档强烈推荐2018年全国初中数学联合竞赛试题参考答案及评分标准第4页（共7页）精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有。

2018-2019年人教版八年级上册数学竞赛试题（含答案）2018-2019学年度上期八年级语文试卷27分）(2分)()/荷重贝壳/金蝉脱壳难解难分/在劫难逃/洼陷针灸/脍炙人口悠然自得/生死攸关/供认押解/浑身解数锐不可当/势不可挡/僻静淹没/掩耳盗铃棱角分明/盛气凌人(2分) ()碧螺春无人问津万古常青引申义天伦之乐张皇失措哈蜜瓜袖手旁观惟妙惟肖练习簿明辩是非穷困潦倒）（2分）面对实力羸弱的香港东方队时，以摧枯拉朽的姿态横扫从空中俯瞰，早春时节的南方大地色彩斑斓，处处流淌着春的气息。

）（2分）38个实验区，从今年起进行课改实验。

（6分）《红星照耀中国》又名《》是国著名记者的(3分)（3分）（8分））树树皆秋色，。

（2）《野望》中抒发孤独抑郁之情的句子是：，。

（3）崔颢在《黄鹤楼》中，以起伏辗转的文笔表现缠绵的乡愁的诗句是： , 。

（4）《记承天寺夜游》中写景的句子是： , , 。

7.阅读下面文段，完成后面的问题。

（5分）新华网喀布尔12月17日电（记者张海波余智骁）阿富汗警方人士17日说，东部霍斯特省当天发生一起针对美军的自杀式炸弹袭击，造成1名阿平民死亡、3人受伤。

霍斯特省纳迪尔沙阿库特地区警察局局长卢特特富拉汉当天对记者说，一名身缠炸药的男子当天驾驶汽车在纳迪尔沙阿库特地区向美军车队发动袭击。

爆炸没有造成美军人员伤亡，却给附近的平民带来了不幸。

目前还没有组织或个人声称对这次袭击事件负责。

阿富汗反政府武装频繁使用自杀式袭击等手段对付外国军队及阿政府官员和军警。

今年以来阿富汗已发生110多起自杀式袭击事件，造成约280人死亡，其中大部分是平民。

（1）请用“”画出本则消息的导语。

（2分）（2）请给本则新闻拟写一个标题。

（3分）二、现代文阅读（28分）（一）阅读下文，回答问题。

（15分）九岁的病榻苏童①我最初的生病经验产生于一张年久失修的藤条躺椅上，那是一个九岁男孩的病榻。

②那年我九岁，不知道为什么会得那种动不动就要小便的怪病，不知道小腿上为什么会长出无数红色疹块，也不知道白细胞和血小板减少的后果到底有多严重。

人教版 八年级数学上册 竞赛专题：整式的乘除（含答案）【例1】（1）若n 为不等式2003006n>的解，则n 的最小正整数的值为 ．（2）已知21x x +=，那么432222019x x x x +--+= ．（3）把26(1)x x -+展开后得121121211210a x a x a x a x a +++++，则121086420a a a a a a a ++++++= ．（4）若543237629()()()()()x x x x x x a x b x c x d x e -+-++=-----则ab ac ad ae bc bd be cd ce de +++++++++= ．解题思路：对于（1），从幂的乘方逆用入手；对于（2），目前无法求x 值，可考虑高次多项式用低次多项式表示；对于（3），它是一个恒等式，即在x 允许取值范围内取任何一个值代入计算，故可考虑赋值法；对于（4），可考虑比较系数法．【例2】已知252019x=，802019y=，则11x y+等于（ ） A ．2 B ．1 C ．12D ．32解题思路：,x y 为指数，我们无法求出,x y 的值，而11x y x y xy++=，所以只需求出,x y xy +的值或它们的关系，于是自然想到指数运算律．【例3】设,,,a b c d 都是正整数，并且5432,,19a b c d c a ==-=，求d b -的值．（江苏省竞赛试题） 解题思路：设5420326,a b m c d n ====，这样,a b 可用m 的式子表示，,c d 可用n 的式子表示，通过减少字母个数降低问题的难度．【例4】已知多项式2223286(2)(2)x xy y x y x y m x y n +--+-=++-+，求3211m n +-的值．解题思路：等号左右两边的式子是恒等的，它们的对应系数对应相等，从而可考虑用比较系数法．【例5】是否存在常数,p q 使得42x px q ++能被225x x ++整除？如果存在，求出,p q 的值，否则请说明理由．解题思路：由条件可推知商式是一个二次三项式（含待定系数），根据“被除式=除式×商式”，运用待定系数法求出,p q 的值，所谓,p q 是否存在，其实就是关于待定系数的方程组是否有解．【例6】已知多项式432237x x ax x b -+++能被22x x +-整除，求ab的值． （北京市竞赛试题） 解题思路：本题主要考查了待定系数法在因式分解中的应用．本题关键是能够通过分析得出当2x =-和1x =时，原多项式的值均为0，从而求出,a b 的值．当然本题也有其他解法．能力训练A 级1．（1）24234(0.25)1⨯--= ． （2）若23n a=，则621n a -= ．2．若2530x y +-=，则432xy． 3．满足200300(1)3x ->的x 的最小正整数为 ．4．,,,a b c d 都是正数，且23452,3,4,5a b c d ====，则,,,a b c d 中，最大的一个是 ． 5．探索规律：133=，个位数是3；239=，个位数是9；3327=，个位数是7；4381=，个位数是1；53243=，个位数是3；63729=，个位数是9；…那么73的个位数字是 ，303的个位数字是 ． 6．已知31416181,27,9a b c ===，则,,a b c 的大小关系是（ ） A ．a b c >>B ．a c b >>C ．a b c <<D ．b c a >>7．已知554433222,3,5,6a b c d ====，那么,,,a b c d 从小到大的顺序是（ ） A ．a b c d <<< B ．a b d c <<< C ．b a c d <<< D ．a d b c <<<8．若11222,22n n n n x y +--=+=+，其中n 为整数，则x 与y 的数量关系为（ ）A ．4x y =B ．4y x =C ．12x y =D ．12y x =9．已知23,26,212,abc===则,,a b c 的关系是（ ） A ．2b a c <+B ．2b a c =+C ．2b a c >+D ．a b c +>10．化简4322(2)2(2)n n n ++-得（ ） A ．1128n +- B ．12n +-C ．78D ．7411．已知2233447,49,133,406ax by ax by ax by ax by +=+=+=+=， 试求171995()6()2x y xy a b ++-+的值．12．已知2267314(23)(3)x xy y x y a x y b x y c --+++=-+++．试确定,,a b c 的值．13．已知323x kx ++除以3x +，其余数较被1x +除所得的余数少2，求k 的值．B 级1．已知23,45,87,abc===则28a c b+-= ．2．（1）计算：2019201920192019201973153735+⎛⎫⨯ ⎪+⎝⎭= ． （2）如果5555555555555554444666666233322n ++++++++⨯=+++，那么n = ． 3．（1）1615与1333的大小关系是1615 1333（填“＞”“＜”“＝”）．（2）201920193131++与201920203131++的大小关系是：201920193131++ 201920203131++（填“＞”“＜”“＝”）．4．如果210,x x +-=则3223x x ++= ．5．已知55432(2)x ax bx cx dx ex f +=+++++，则164b d f ++= ． 6．已知,,a b c 均为不等于1的正数，且236,a b c -==则abc 的值为（ ）A ．3B ．2C ．1D ．127．若3210x x x +++=，则27261226271x x x x x x x ---+++++++++的值是（ ）A ．1B ．0C ．—1D ．28．如果328x ax bx +++有两个因式1x +和2x +，则a b +=（ ） A ．7B ．8C ．15D ．219．已知12320182019,,,,a a a a a 均为正数，又122018232019()()M a a a a a a =++++++，122019232020()()N a a a a a a =++++++，则M 与N 的大小关系是（ ）A ．M N =B ．M N <C ．M N >D ．关系不确定10．满足22(1)1n n n +--=的整数n 有（ ）个A ．1B ．2C ．3D ．411．设,,,a b x y 满足2233443,7,16,42,ax by ax by ax by ax by +=+=+=+=求55ax by +的值．12．若,,,x y z w 为整数，且x y z w >>>，52222208xyzw+++=，求2020(1)x y z w +++-的值．13．已知,,a b c 为有理数，且多项式32x ax bx c +++能够被234x x +-整除． （1）求4a c +的值； （2）求22a b c --的值；（3）若,,a b c 为整数，且1c a >≥．试比较,,a b c 的大小．参考答案例1(1)(n 2)100＞(63)100，n 2 ＞216，n 的最小值为15．(2)原式＝x 2(x 2＋x )＋x (x 2 ＋x )－2(x 2＋x ) ＋2019＝ x 2＋x －2＋2019＝2018 (3)令x ＝1时，a 12＋a 11＋a 10＋…＋a 2＋a 1＋a 0＝1， ① 令x ＝－1时，a 12 –a 11＋a l 0－…＋n 2－a l ＋a 0 ＝729 ② 由①＋②得：2(a 12＋a l 0＋a 8＋…＋a 2 ＋a 0)＝730． ∴a 12 ＋a 10 ＋a 8 ＋a 6＋a 4 ＋a 2＋a 0 ＝365． (4)所有式子的值为x 3项的系数，故其值为7． 例2 B 提示：25xy ＝2 019y ， ① 80xy ＝2 019x ， ②①×②，得：(25×80)xy ＝2019x ＋y ，得：x ＋ y ＝xy ．例3 设a ＝m 4，b ＝m 5，c ＝n 2，d ＝n 3，由c －a ＝19得，n 2－m 4＝19，即(n ＋m 2) (n －m 2)＝19，因19是质数，n ＋m 2，n －m 2是自然数，且n ＋m 2＞n －m 2，得⎩⎪⎨⎪⎧n ＋m 2＝19n －m 2＝1，解得n ＝10，m ＝3，所以d －b ＝103－35 ＝757例4 －78提示：由题意知：2x 2＋3xy －2y 2－x ＋8y －6＝2x 2＋3xy －2y 2＋(2m ＋n )x ＋(2n －m )y ＋mn ．∴⎩⎪⎨⎪⎧2m ＋n ＝－12n －m ＝8mn ＝－6，解得⎩⎨⎧m ＝－2n ＝3，∴m 3＋1n 2－1 ＝－78倒5提示：假设存在满足题设条件的p ，q 值，设(x 4＋px 2＋q )＝(x 2＋2x ＋5)(x 2＋mx ＋n )，即 x 4＋px 2＋q ＝x 4＋(m ＋2)x 3＋(5＋n ＋2m )x 2＋(2n ＋5m )x ＋5n ，得⎩⎨⎧m ＋2＝05＋n ＋2m ＝p 2n ＋5m ＝05n ＝q ，解得⎩⎨⎧m ＝－2n ＝5p ＝6q ＝25，故存在常数p ，q 且p ＝6，q ＝25，使得x 4＋px 2＋q 能被x 2＋2x ＋5整除．例6解法1 ∵x 2＋x －2＝(x ＋2) (x －1)，∴2x 4－3x 3＋ax 2＋7x ＋b 能被(x ＋2)(x －1)整除，设商是A ． 则2x 4－3x 3＋ax 2＋7x ＋b ＝A (x ＋2)(x －l )，则x ＝－2和x ＝1时，右边都等于0，所以左边也等于0．当x ＝－2时，2x 4－3x 3＋ax 2＋7x ＋b ＝32＋24＋4a －14＋b ＝4a ＋b ＋42＝0， ① 当x ＝1时， 2x 4－3x 3＋ax 2＋7x ＋b ＝2－3＋a ＋7＋b ＝a ＋b ＋6＝0． ② ①－②，得3a ＋36＝0，∴ a ＝－12， ∴ b ＝－6－a ＝6． ∴a b ＝－126＝－2 解法2 列竖式演算，根据整除的意义解2243243232322225(9)22372245(4)75510(9)3(9)(9)2(9)(12)2(9)x x a x x x x ax x bx x x x a x x b x xx a x x ba x a x a a xb a -+++--++++--++++--++-++-+-+--+++∵2x 4－3x 3＋ax 2＋7x ＋b 能被x 2＋x －2整除，∴⎩⎨⎧－12－a ＝0b ＋2(a ＋9)＝0，即⎩⎨⎧a ＝－12b ＝6，∴a b ＝－2A 级1．(1) －5 (2)53 2．8 3．7 4．6 5．7 9 6．A 7．D 提示：a ＝(25)11，b －(34)11，c ＝(53)11，d ＝(62)11 8．A 9．B 10．C 11．4800 12．a ＝4．b ＝4，c ＝113． 提示：令x 3 ＋kx 2＋3＝(x ＋3) (x 2＋ax ＋6)＋r 1，x 3＋kx 2＋3＝( x ＋1) (x 2＋cx ＋d )＋r 2，令x ＝－3，得r 1＝9k －24．令x ＝－1，得r 2＝k ＋2，由9k －24＋2＝k ＋2， 得k ＝3．B 级1．1891252． (1)949(2)123．(1) ＜ 1516 ＜1615＝264，3 313 ＞3213＝265 ＞264． (2) ＞ 提示：设32 000 ＝x ．4．4 5．512 提示：令x ＝±2． 6．C 提示：由条件得a ＝c －3 ，b ＝c 2 ，abc ＝c －3·c 2·c ＝1 7．C 8．D 9．C 10．D11．由ax 2＋by 2 ＝7，得(ax 2＋by 2)(x ＋y )＝7(x ＋y )，即ax 3－ax 2y ＋bxy 2＋by 3 ＝7(x ＋y )，(ax 3＋by 3)－xy (ax ＋by )－7(x ＋y )． ∴16＋3xy ＝ 7(x ＋y )． ①由ax 3 ＋by 3＝16，得(ax 3＋by 3)(x ＋y ) ＝16(x ＋y )，即ax 4 ＋ax 3 y ＋bxy 3＋by 4 ＝16(x ＋y )，（ax 4＋by 4)＋xy (a 2x ＋b 2y )＝16(x ＋y ）． ∴42＋7xy ＝16(x ＋y ）． ② 由①②可得，x ＋y ＝－14，xy ＝－38．由a 2x ＋b 2y ＝42，得（a 4x ＋b 4y ）（x ＋y ）＝42×（－14）， （a 5x ＋b 5y ）＋xy （a 3x ＋b 3y ）＝－588，55ax by +＋16×（－38）＝－588．故55ax by +＝20． 12． ()20191x y z w +++-＝()201942131+---＝1．13．（1）∵（x －1）（x ＋4)＝2x ＋3x －4， 令x －1＝0，得x ＝1；令x ＋4＝0，得x ＝－4． 当x ＝1时，得1＋a ＋b ＋c ＝0； ① 当x ＝－4时，得－64＋16a －4b ＋c ＝0． ② ②－①，得15a －5b ＝65，即3a －b ＝13． ③ ①＋③，得4a ＋c ＝12．（2）③－①，得2a －2b －c ＝14．（3）∵c ≥a ＞1，4a ＋c ＝12，a ，b ，c 为整数， ∴1＜a ≤125，则a ＝2，c ＝4． 又a ＋b ＋c ＝－1，∴b ＝－7，．∴c ＞a ＞b ．。

2018年初二数学练习一、选择题（满分25分，每小题只有一个正确答案，答对得5分，将答案写在下面相应的空格中）13=，则220181x x x ++的值是（A ）2020． （B ）12020． （C ）2025． （D ）12025． 2．在非等腰三角形中，一个内角等于另两个内角的差，且一个内角是另一个内角的2倍．已知该三角形的最小边长等于1cm ，则这个三角形的面积是（A ）1 cm 2． （B cm 2． （C cm 2． （D ）2 cm 2． 3．n 是偶数，若从1开始，前n 个正整数的和的尾数是数字8，则后继的n 个正整数的和的尾数是数字（A ）6． （B ）4． （C ）2． （D ）0．4．如图，P (x p , y p )为反比例函数2y x=在平面直角坐标系x-O-y 的第一象限图像上一点，过点P 作x 轴、y 轴的平行线分别交10y x=在第一象限的图像于点A 和B ，则△AOB 的面积等于（A ）26． （B ）24． （C ）22． （D ）20．5．将数字和为11的自然数按由小到大的顺序排成一个数串，第m 个数是2018，则m 是.（A ）134． （B ）143． （C ）341． （D ）413．二、填空题（满分35分，每小题7分，将答案写在下面相应的空格中）1．295的约数中大于1000000的共有______个．2．若x ，y 都是自然数，关于x ，y 的方程[2.018x ]+[5.13y ]=24的解(x , y )共有______个．（其中[x ]表示不大于x 的最大整数）3．D 为锐角△ABC 内一点，满足AD =DC ，∠ADC =2∠DBC ， AB =12，BC =10，则△BDC 的面积等于______．4．已知x 1, x 2, …, x n 中每一个x i (i =1, 2, …, n )的数值只能取 −2, 0, 1中的一个，且满足x 1+x 2+…+x n =−17，x 12+x 22+…+x n 2=37， 则(x 13+x 23+…+x n 3)2的值为______．5．在1~n 这n 个正整数中，正约数个数最多的那些数叫做这前n 个正整数中的“旺数”，如在正整数1~20中，正约数个数最多的数是12, 18, 20，所以12, 18, 20都是正整数1~20中的“旺数”，在正整数1~100中的所有“旺数”的最小公倍数是______．三、（满分10分）正整数a , b , c , d 满足a 2−ab +b 2=c 2−cd +d 2，求证：a +b +c +d 是合数．四、（满分15分）三个斜边彼此不等的等腰直角三角形ADC ，DPE 和BEC ，如图所示，其中AD =CD ，DP =EP ，BE =CE ；∠ADC =∠DPE =∠BEC =90°，求证：P 是线段AB 的中点．ADCPB五、（满分15分）求证：在十进制表示中，数29的某个正整数幂的末三位数字是001．2018年北京市中学生数学竞赛初二年级试题及参考解答2018年5月13日8:30～10:30.一、选择题（满分25分，每小题只有一个正确答案，答对得5分，将答案写在下面相应的空格中）题号12345答案DBCBA13+=，则220181x x x ++的值是（A ）2020．（B ）12020．（C ）2025．（D ）12025．答：D ．3+=两边平方，得129x x ++=，即17x x +=．所以220181120182025x x x x x ++=++=，即21=201812025x x x ++．2．在非等腰三角形中，一个内角等于另两个内角的差，且一个内角是另一个内角的2倍．已知该三角形的最小边长等于1cm ，则这个三角形的面积是（A ）1cm 2．（B ）2cm 2．（C ）2cm 2．（D ）2cm 2．答：B ．理由：设三角形的内角为A ，B ，C ，且B =C −A ，则A +(C −A )+C =180°，得C =90°．若最大角C 是另一个内角的2倍，易知三角形为等腰直角三角形，与题设“非等腰三角形”的条件不符，因此只能是另一个内角是第三个内角的2倍．不妨设A =2B ，可得A =60°，B =30°．因此角B 的对边AC =1cm ，斜边AB =2cm ，另一直角边BC =．所以这个三角形的面积是1122⨯(cm 2)．3．n 是偶数，若从1开始，前n 个正整数的和的尾数是数字8，则后继的n 个正整数的和的尾数是数字（A ）6．（B ）4．（C ）2．（D ）0．答：C ．解：设n =2k ，记S 为前n 个正整数的和，D 为后继的n 个正整数(由2k +1到4k )的和，则S =k (2k +1)2(214)(61).2k k k D k k ++==+数S 和D 的最后数字只依赖于数k 的最后数字．如果k 是奇数，那么S 是奇数，不合题意，于是k 是偶数，它的尾数取自0,2,4,6或8，则S 的结尾对应为0,0,6,8或6．依题意，k 应当以6结尾，这样D 的尾数就是(661)6⨯+⨯的尾数，即为2．4．如图，P (x p ,y p )为反比例函数2y x=在平面直角坐标系x -O -y 的第一象限图像上一点，过点P 作x 轴、y 轴的平行线分别交10y x=在第一象限的图像于点A 和B ，则△AOB 的面积等于（A ）26．（B ）24．（C ）22．（D ）20．答：B ．理由：过点A ，B 分别作坐标轴的平行线，出现矩形MKON ，如右图，有KM =ON =10p x ，KA =OL =y p ，NM =OK =10py ，NB =OT =x p ．△AOB 的面积=长方形OKMN 的面积−△AOK 的面积−△NOB 的面积−△AMB 的面积=101011011011010()()222p p p p p p p p p p y x x y y x y x y x ⋅-⋅⋅-⋅⋅---=100110055(10102)222-----+=24．另解：如图，联结OP ，LB ，TA ，可知△AOB 的面积=△AOP 的面积+△POB 的面积+△APB 的面积=11011011010()()()()222p p p p p p p p p p x y y x x y y x y x -+-+--=111100(102)(102)(10102)2222-+-+--+=24．5．将数字和为11的自然数按由小到大的顺序排成一个数串，第m 个数是2018，则m 是（A ）134．（B ）143．（C ）341．（D ）413．答：A理由：在一位数中没有数字和为11的数．两位数中有29,38,47,56,65,74,83,92这8个数．在三位数xyz 中，当x =1时，y 可取1~9这9个数，对应的z 取9~1，共9个数；同法可得：当x =2时，y 可取0~9这10个数，对应的z 取9~0，共10个数；当x =3时，p有308,317,326,335,344,353,362,371,380这9个数；当x=4时，有407,416,425,434, 443,452,461,470这8个数；当x=5时，有506,515,524,533,542,551,560这7个数；当x=6时，有605,614,623,632,641,650这6个数；当x=7时，有704,713,722,731,740这5个数；当x=8时，有803,812,821,830这4个数；当x=9时，有902,911,920这3个数．因此，在三位数xyz中，数字和为11的数共有9+10+9+8+7+6+5+4+3=61个．在四位数1xyz中，数字和为11的数相当于求数字和为10的三位数xyz，当x=0时，y可取1~9这9个数，对应的z取9~1的数，共9个数；同法可得：当x=1,2,3,4, 5,6,7,8,9时，数字和为10的三位数xyz分别有10,9,8,7,6,5,4,3,2个；因此在四位数1xyz中，数字和为11的数共有9+10+9+8+7+6+5+4+3+2=63个．在2xyz中，数字和为11的数由小到大有2009,2018．因此2018是该数串中的第8+61+63+2=134个数．二、填空题（满分35分，每小题7分，将答案写在下面相应的空格中）1．295的约数中大于1000000的共有______个．答：76．解：因为295有96个正约数：20,21,22,…,294,295，又210=1024，从而220=210×210=1048576＞1000000．又219=1048576÷2=524288＜1000000，所以295的约数中大于1000000的共有96−20=76个．2．若x，y都是自然数，关于x，y的方程[2.018x]+[5.13y]=24的解(x,y)共有______个．（其中[x]表示不大于x的最大整数）答：3．解：因为x，y都是自然数，且5.13×5=25.65＞24，所以y只能取4，3，2，1，0．当y=4时，[5.13×4]=[20.52]=20，所以[2.018x]=24−20=4，即x=2；当y=3时，[5.13×3]=[15.39]=15，所以[2.018x]=24−15=9，无合适的x值；当y=2时，[5.13×2]=[10.26]=10，所以[2.018x]=24−10=14，即x=7；当y=1时，[5.13×1]=[5.13]=5，所以[2.018x]=24−5=19，无合适的x值；当y=0时，[5.13×0]=[0]=0，所以[2.018x]=24−0=24，即x=12．方程[2.018x]+[5.13y]=24的所有解为(2,4)，(7,2)，(12,0)，共3个．3．D为锐角△ABC内一点，满足AD=DC，∠ADC=2∠DBC，AB=12，BC=10，如图，则△BDC的面积等于______．答：解：设∠DBC =θ，则∠ADC =2θ．以D 为旋转中心，旋转△BDC 到△ADP 的位置，如图．则AD=DC ，DP =DB ，AP =CB =10，∠DP A =∠DBC =θ，∠PDA =∠BDC ，即∠PDC +∠CDA =∠BDP +∠PDC ，所以∠BDP =∠ADC =2θ．在等腰△BDP 中，作DK ⊥BP 于点K ，则∠BPD =12(180°−2θ)=90°−θ．所以，∠APB =∠APD +∠DPB =θ+(90°−θ)=90°．即△ABP 为直角三角形．在直角△ABP中，BP ===作DH ⊥AP 于点H ，则PHDK 为矩形，DH =KP =12BP．所以△BDC 的面积=△PDA 的面积=1102⨯4．已知x 1,x 2,…,x n 中每一个x i (i =1,2,…,n )的数值只能取−2,0,1中的一个，且满足x 1+x 2+…+x n =−17，x 12+x 22+…+x n 2=37，则(x 13+x 23+…+x n 3)2的值为______．答：5041．解：设x 1,x 2,…,x n 中有p 个x i 取1，q 个x i 取−2，其余的x i 取0，可得217437p q p q -=-⎧⎨+=⎩，解得1.9p q =⎧⎨=⎩所以x i (i =1,2,…,n )中有1个取1，有9个取−2，其余的x i 取0．因此(x 13+x 23+…+x n 3)2=(1×13+9×(−2)3)2=(−71)2=5041．5．在1~n 这n 个正整数中，正约数个数最多的那些数叫做这n 个正整数中的“旺数”，比如，正整数1~20中，正约数个数最多的数是12,18,20，所以12,18,20都是正整数1~20中的“旺数”，在正整数1~100中的所有“旺数”的最小公倍数是______．答：10080．解：首先，前100个正整数的质因数分解式中，最多含有三个不同的质因数．这是因为最小的四个质数之积为2×3×5×7=210，已超过100．其次为使约数个数尽可能多，应使所含的质因数尽可能小，于是可以通过试算、分类枚举来确定正约数个数最大为12的数：只含一个质因数的正因数最多的是26=64，它有7个正约数，正约数小于12．对于只含有两个不同质因数的情况，正约数个数为12的是：23×32(=72)，25×3(=96)．对于含有三个不同质因数的情况，正约数个数为12的是：22×3×5(=60)，2×32×5(=90)，22×3×7(=84)．可见，在前100个正整数中,正约数为12个的“旺数”只有：60，72，84，90，96这5个．因此在前100个正整数中，所有“旺数”的最小公倍数是25×32×5×7=10080．BKP CA HD三、（满分10分）正整数a ,b ,c ,d 满足a 2−ab +b 2=c 2−cd +d 2，求证：a +b +c +d 是合数．证明：记s =a +b +c +d ，由已知条件，(a +b )2−(c +d )2=3(ab −cd )，所以(a +b −c −d )s =3(ab −cd )=3(ab −c (s −a −b −c ))=3(a +c )(b +c )−3cs ，因此s 整除3(a +c )(b +c )．易知s 的每个质因数p 都是3(a +c )(b +c )的因数，即p 是3,a +c ,b +c 的因数，所以s 的每一个质因数p 不超过3,a +c ,b +c 中的最大值，因为s 大于3,a +c ,b +c 中的最大值，则s =p ·m （整数m ≥2）．即数s 是合数．四、（满分15分）三个斜边彼此不等的等腰直角三角形ADC ，DPE 和BEC ，如图所示，其中AD=CD ，DP=EP ，BE=CE ；∠ADC =∠DPE =∠BEC =90°，求证：P 是线段AB 的中点．证明：（1）延长DP 至F ，使得PF =PD ，连接FE 、FB ，易知△DEF 为等腰直角三角形，即DE=EF ，∠DEF =90°．所以，∠CED =90°−∠CEF =∠BEF ．又DE=EF ，CE=BE ，所以△CED ≌△BEF ．因此CD=BF ，∠CDE =∠BFE ．（2）连接AP 、BP ，因为AD=CD ，所以在△ADP 与△BFP 中，AD=BF ，∠ADP=∠ADC +∠CDE −∠EDP=90°+∠CDE −45°=∠CDE +45°=∠BFE +∠PFE =∠BFP ．又DP=FP ，所以△ADP ≌△BFP ．因此AP=BP ，∠APD=∠BPF ．（3）如果CD ∥PE ，则A 、D 、P 三点共线，B 、F 、P 三点共线，又D 、P 、F 三点共线，所以A 、P 、B 三点共线．由AD=BF ，DP=PF ，所以AP =AD+DP=BF +PF=BP ．因此P 是线段AB 的中点．如果CD 与PE 不平行，由于A ，B 在直线DF 的两侧，而D 、P 、F 三点共线，∠APD=∠BPF ，故A ,P ,B 三点共线，即点P 在线段AB 上，因为已证AP=BP ，所以P 是线段AB 的中点．五、（满分15分）求证：在十进制表示中，数29的某个正整数幂的末三位数字是001．证明：因为末三位数只有000到999这1000中不同的排列情况.而291,292,…,291001是1001个29的不同的幂数，根据抽屉原理，其中存在两个29的不同的幂数，它们的末三位数字是相同的．设末三位数字相同的这两个幂数是29k 与29l ，1≤l ＜k ≤1001，因此29k −29l 被1000整除，即29l (29k −l −1)被1000整除．但(29l ,1000)=1，所以29k −l −1被1000整除，即29k l 的末三位数字是001．这就证明了存在29的某个正整数幂的末三位数字是001．A DCPEBF。

2018年全国初中数学联赛试题参考答案和评分标准精品2018年全国初中数学联合竞赛试题参考答案及评分标准说明：评阅试卷时，请依据本评分标准。

第一试，选择题和填空题只设7分和0分两档；第二试各题，请按照本评分标准规定的评分档次给分。

如果考生的解答方法和本解答不同，只要思路合理，步骤正确，在评卷时请参照本评分标准划分的档次，给予相应的分数。

第一试一、选择题：（本题满分42分，每小题7分）1.已知$a=1+\frac{1}{2+1}$，$b=3-2$，$c=6-2$，那么$a,b,c$的大小关系是（）A。

$a<b<c$B。

$a<c<b$XXX<a<c$D。

$b<c<a$答】C.因为 $\frac{1}{2+1}=\frac{1}{3}$，所以$a=1+\frac{1}{3}=\frac{4}{3}$，$b=1$，$c=4$。

因为 $\frac{1}{3}<1$，所以$a<\frac{4}{3}+1=\frac{7}{3}<c$，所以 $b<a<c$。

2.方程$x^2+2xy+3y^2=34$的整数解$(x,y)$的组数为（）A。

3B。

4C。

5D。

6答】B.方程即$(x+y)^2+2y^2=34$，显然$x+y$必须是偶数，所以可设$x+y=2t$，则原方程变为$2t^2+y^2=17$。

因为$2t^2\leq 16$，所以$t=\pm 2$，从而可求得原方程的整数解为$(x,y)=(-7,3),(1,3),(7,-3),(-1,-3)$，共4组。

3.已知正方形ABCD的边长为1，E为BC边的延长线上一点，$CE=1$，连接AE，与CD交于点F，连接BF并延长与线段DE交于点G，则BG的长为（）A。

$\frac{65}{26}$B。

$\frac{3}{3}$C。

$\frac{2}{5}$D。

$\frac{9}{4}$答】D.过点C作$CP\parallel BG$，交DE于点P。