卡诺图在其它方面的应用
- 格式:pptx
- 大小:392.57 KB
- 文档页数:6

多变量卡诺图及其在逻辑函数中的应用摘要:卡诺图是在数字电路中十分有用的工具,本文介绍了多变量卡诺图在逻辑函数化简中的应用。
关键词:卡诺图、逻辑函数、化简Multi-variable Karnaugh Map and the Application of it in Logic Function Abstract:Karnaugh map is very useful in the study of digital design, in this article; we have introduce the application of multi-variable Karnaugh map in simplification of logic functions.Key words:Karnaugh map, simplification, logic function.卡诺图(Karnaugh map)是由美国科学家卡诺首先提出的。
在数字电子技术中,卡诺图是逻辑函数真值表的一种图形表示,即用图形表示输入变量与函数之间的逻辑关系。
就n个变量的卡诺图来说,它是由n2个小方格组成,每一小方格代表一个最小项。
在卡诺图中,几何位置相邻(这里的几何位置相邻包括边缘、四角)的小方格在逻辑上也是相邻的,卡诺图用几何位置上的相邻, 形象地表示了组成逻辑函数的各个最小项之间在逻辑上的相邻性。
在数字电路原理与实践课程中,我们常常将卡诺图作为化简逻辑函数的工具。
利用卡诺图化简逻辑函数的方法称为卡诺图化简法或图形化简法。
化简时依据的基本原理就是具有相邻性的最小项可以合并,以此消去不同的因子。
由于在卡诺图上几何位置相邻与逻辑上的相邻性是一致的,因而我们能够从卡诺图上直观地找出那些具有相邻性的最小项并将其合并、化简。
利用卡诺图合并最小项的规则如下:如果两个最小项逻辑相邻,那么二者可以合并成为一项并消去一对因子,合并后的结果中只包含公共因子。

离散数学是数学的一个分支,研究的是离散结构和离散型对象的性质。
其中,布尔函数是离散数学中的重要概念之一,而卡诺图则是布尔函数的一种可视化工具和简化方法。
布尔函数是指由布尔代数中的逻辑运算(如与、或、非)构成的函数。
它将一组布尔变量映射到布尔值的集合上。
布尔函数的输入和输出都只能是0(假)和1(真)。
布尔函数在电子电路设计、计算机科学、密码学等领域有着广泛的应用。
在离散数学中,我们通常用真值表来表示布尔函数,并通过逻辑运算的组合来描述其性质。
然而,随着布尔函数的规模增大,真值表的表示变得复杂而不直观。
卡诺图(Karnaugh Map)成为一种常用的工具,用于优化和简化布尔函数的表示。
卡诺图是由一张由2的幂次方的格子组成的表格构成,表格的每个格子表示布尔函数的一个可能输入组合。
通过将真值表中的不同输入组合映射到卡诺图的格子上,并将对应的输出值填入格子中,我们可以更加直观地观察和分析布尔函数的模式。
利用卡诺图,我们可以进行布尔函数的最小化和化简操作。
最小化操作是指通过合并相邻格子中具有相同输出值的格子,从而得到一个更简洁的布尔函数表示。
而化简操作是指通过合并相邻格子中具有相同输入变量的格子,从而得到一个更简洁的真值表表示。
卡诺图的使用规则是相邻格子之间仅有一个变量取值不同。
通过观察这种变化的模式,可以找到多个相邻格子可以合并的可能。
通过将相邻格子合并,我们可以得到一个更简化的布尔函数或真值表表示,从而减少计算复杂度。
卡诺图的优点是直观且易于理解。
通过观察格子的组合模式,我们可以更容易地理解和分析布尔函数的性质。
此外,卡诺图还可以用于表示多个布尔函数之间的关系,进一步帮助我们进行逻辑分析和优化。
总结来说,离散数学中的布尔函数与卡诺图是相辅相成的概念。
布尔函数作为离散数学中的重要概念,用于描述逻辑运算和电子电路的行为。
而卡诺图作为布尔函数的可视化工具和简化方法,帮助我们更直观地观察和分析布尔函数的模式,进而进行最小化和化简操作。


卡诺图应用研究摘要在对卡诺图的应用上,由于很多课本都很零散地作了分析,而且是本着用到提到,不用不提的思想。
为此,本文针对卡诺图应用研究作出了较为系统的总结。
采取由易到难,由一方面到多方面的应用分析。
通过系统总结,可以让读者更为直观,全面的认识卡诺图,了解卡诺图,应用卡诺图。
关键词卡诺图;逻辑函数;最小项Abstract: this paper summarized the applied research of the Karnaugh map more systematically. This paper analyzed the application from easy to difficult, on the one hand to a wide range. Systematic summary to give readers a more intuitive and comprehensive understanding of the Karnaugh map for the Karnaugh map, the application Karnaugh map.Key words: Karnaugh map; logic function; minterm 中图分类号:TP33文献标识码:A文章编号:2095-2104(2012)02-随着数字技术的快速发展,现代电子设备已经从模拟化向数字化转变。
目前,大多数电路只在信号采集、微弱信号放大、高频大功率输入等局部采用模拟电路,其余部分广泛采用数字技术及数字处理电路。
因此,对数字电路的分析与研究成为电子工程技术人员必须掌握的知识。
在数字电子技术中数字逻辑电路的设计是非常重要的,而卡诺图在逻辑电路设计中又起到非常重要的作用,所以本文对卡诺图的应用作出进一步的分析与讨论。
1 逻辑函数卡诺图运用代数法化简逻辑函数时,必须熟练掌握逻辑代数的基本公式并具备一定的技巧。



数字电路中卡诺图的灵活应用刘玲【摘要】卡诺图是一种体现逻辑相邻关系的几何图形,多用于逻辑函数的表示和化简.通过实例,展示了卡诺图在求解逻辑函数的反函数、判断竞争冒险现象以及组合逻辑电路和时序逻辑电路设计中的应用.灵活运用卡诺图,将大大简化数字电路的分析和设计过程,起到事半功倍的效果.【期刊名称】《数字技术与应用》【年(卷),期】2016(000)005【总页数】2页(P51-52)【关键词】卡诺图;数字电路;逻辑函数;应用【作者】刘玲【作者单位】四川工商学院四川成都 611745【正文语种】中文【中图分类】TN79卡诺图是由2n个方格组成的、并能体现最小项逻辑相邻关系的几何图形。
从卡诺图上能直观地找出具有相邻关系的最小项并将其合并化简,这种方法无需特殊的技巧和熟记公式,只要按照正确的步骤和一定的化简原则就能容易地得到最简结果,因此卡诺图在逻辑函数化简中得以广泛的应用。
事实上,卡诺图除了可以化简逻辑函数,还有很多其他的用途,只要灵活运用,即可大大化简数字电路的分析和设计过程。
本文通过实例,阐述了卡诺图在逻辑函数化简之外的几点巧妙应用。
2.1 利用卡诺图求逻辑函数的反函数利用反演规则可以比较容易地求出逻辑函数的反函数,但得到的表达式并一定最简。
如果利用卡诺图,对逻辑函数表达式中没有出现的最小项之和进行化简,即采用包围0的方法,得到的表达式即为逻辑函数反函数的最简与或式。
例1:求逻辑函数的反函数。
解:画出逻辑函数的卡诺图(如图1),在卡诺图中对0加包围圈,可求出反函数的最简与或式,即得2.2 利用卡诺图分析组合逻辑电路中的竞争冒险在组合逻辑电路中,门电路的两个不同电平输入信号同时向相反方向转换的现象称为竞争,由竞争而可能产生输出干扰脉冲的现象称为冒险。
为保证电路正常工作,设计时需注意判断和消除竞争卡诺图法的步骤是:先画出逻辑函数的卡诺图,然后在卡诺图上画出与表达式中的乘积项相对应的包围圈,如果圈与圈之间出现相切,且相切处没有被其他圈包围,即可判断出现竞争冒险现象。


用卡诺图化简或——与表达式引言:随着电子技术的飞快发展,卡诺图已经变成了逻辑设计中十分重要的数学工具。
卡诺图因为它能用图形将复杂的逻辑函数形象直观的表示出来。
所以,卡诺图在数字电子技术当中应用十分的广泛。
数字电子技术当中的逻辑函数是“或”、“与”、“非”复合而成,所以使用卡诺图分析逻辑函数是具有现实意义的。
1.使用卡诺图的优点化简或——与函数可以使用卡诺图化简法和公式分析法来进行化简。
但是在现实当中的逻辑函数化简当中,逻辑函数可能十分复杂,化简需要熟记大量的基本公式。
不仅如此还需要能够灵活巧妙的使用基本公式、方法,所以使公式化简法显得十分繁琐,所需的技巧性十分强。
但是使用卡诺图时不仅可以用于多输入变量的逻辑函数化简,还可以用图像来直观、快速表示出最简表达式,所以卡诺图是一种十分实用的化简方法。
2. 卡诺图2.1卡诺图概述一个逻辑函数的卡诺图就是讲此函数的最小项表达式中的各最小项相应地填入一个特定的方格图内,从此方格图称为卡诺图。
卡诺图的实质就是真值表的图形化,使得最小项排列得更紧凑,更便于化简。
卡诺图中最小项的排列方案不是惟一的;变量的坐标值0表示相应变量的反变量,1表示相应变量的原变量;各小方格依变量顺序取坐标值,所得二进制数对应的十进制数即相应最小项的下标i。
对于n个变量的逻辑函数有2^n个最小项。
如果把每个最小项用一个小方格表示,再讲这些小方格按格雷码顺序排列,就可以构成n个变量的卡诺图。
以4变量为例的卡诺图表一2.2卡诺图特点卡诺图的特点是:几何位置相邻的最小项在逻辑上也是相邻的。
即相邻的两个最小项只有一个变量不同,这是用卡诺图化简逻辑函数的主要依据。
正如表一中m4与m5两个相邻相中只有D与非D两的差别。
2.3卡诺图化简逻辑函数依据卡诺图具有相邻性,若两个相邻的方格均为1,则这两个最小项之和有一个变量可以被消去。
以此为依据通过把卡诺图上相邻最小项的相邻小方格圈起来进行合并,达到用“与”项来代替。
题目:卡诺图化简所应用的逻辑代数原理与方法Topic:Cano figure reduction applied logic algebra principle and method摘要:对卡诺图化简所应用的逻辑代数原理进行讨论,并总结化简的方法,以及卡诺图在其他方面的作用。
关键字:卡诺图,原理,方法,作用。
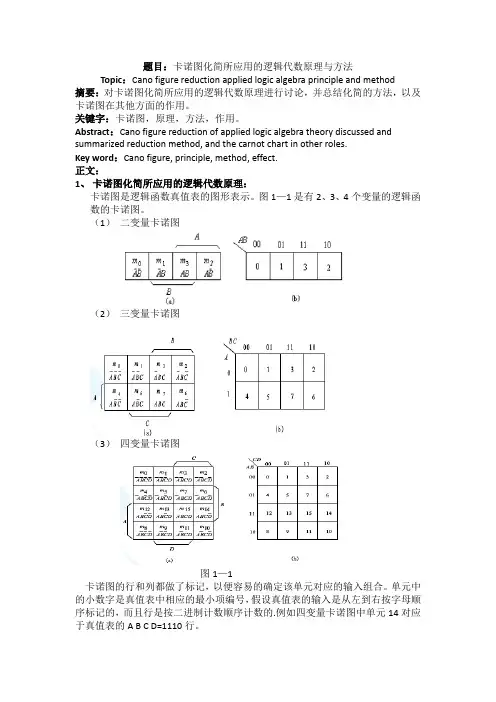
Abstract:Cano figure reduction of applied logic algebra theory discussed and summarized reduction method, and the carnot chart in other roles.Key word:Cano figure, principle, method, effect.正文:1、卡诺图化简所应用的逻辑代数原理:卡诺图是逻辑函数真值表的图形表示。
图1—1是有2、3、4个变量的逻辑函数的卡诺图。
(1)二变量卡诺图(2)三变量卡诺图(3)四变量卡诺图图1—1卡诺图的行和列都做了标记,以便容易的确定该单元对应的输入组合。
单元中的小数字是真值表中相应的最小项编号,假设真值表的输入是从左到右按字母顺序标记的,而且行是按二进制计数顺序计数的.例如四变量卡诺图中单元14对应于真值表的A B C D=1110行。
卡诺图中每个单元都包含函数真值表对应行的信息。
如果对应输入组合的函数值为0时,图中单元内也是0,否则为1.卡诺图的行号和列号采用的是格雷码,才用的这种编码的原因是格雷码的任意两个相邻的代码之间只有一位不同,而且格雷码是循环码。
在卡诺图中的实际用途就是,例如,4变量图的单元13和15是相邻的,它们只有C值不同。
在最小化“积之和”时,因为“项+0=项”,所以“积之和”时函数值为0的项对逻辑函数是没有作用的,只会增加逻辑函数表达式的项,从而增加成本。
故在最小化“积之和”时,只考虑函数值为1的项。
同理可得,当最小化“和之积”时,因为“项*1=项”,所以最小化“积之和”时,只考虑函数值为0的项。

数字电路中卡诺图的应用与研究王珊珊摘要:迄今为止,未见到一本全面阐述卡诺图知识的专著。
本文将卡诺图在数字电路中的应用进行了系统的总结,按其应用的共同特点分为:在逻辑化简上的应用、在逻辑运算上的应用和在解决电路中问题的应用三大类。
在此基础上,对发现的四个未见文献阐述过的问题:在特殊化简中的区域整体现象、用卡诺图圈“0”的方法把函数化简成与或式应该有的前提条件、奇数个逻辑变量的同或与异或相等的卡诺图证明方法和利用无关项在卡诺图化简中的相应说明作了研究,在这四个问题上作了推证,给出了结论并举例加以说明。
关键词:卡诺图应用推证The Applications and Research on The Karnaugh Map in Digital CircuitWangShanshanAbstract:So far, we have not seen any monographs of karnaugh map。
This paper summarizes any situation of applications on Karnaugh map in digital circuit, its application in common is divided into three big parts:The application of the logic simplification 、The application of the logic operation and The application solve the problems in digital circuit 。
Found four problems that no literature expounded on the basis of the summarizes:The overall regional situation in the special simplification、The prerequisite must have in the karnaugh map circle "0" simplification that make logic function into the most simplified、Prove that same-or gate equal else-or gate in odd number logic variable in Karnaugh map and The application of the related items in the K-map simplification,then do research on this four problems,Made a deduction and gives the conclusion with examples。
第9卷第9期 2010年9月 软件导刊
Software Guide VO1.9 NO.9
Sep.2010
卡诺图在软件复杂分支条件简化中的应用 叶如意 (中国标准化研究院,北京100088) 摘 要:举例介绍了一种使用卡诺图对多变量多分支条件的复杂逻辑式同时进行简化。有效解决多分支条件等效简 化、验证多分支条件间是否相互交叉或覆盖全面的方法。结合if_else语句特点,还能更大程度地简化分支条件。 关键词:卡诺图;逻辑简化;分支条件;软件设计 中图分类号:TP301 文献标识码:A 文章编号:1672—7800(2010)09—0107—03
0 引言 在软件开发设计过程中经常需要使用分支条件选择。对于 一些简单的逻辑运算。不需要进行严密的推算就可以验证条件 的正确性、交叉和覆盖情况。但有时会遇到因变量多且逻辑运 算复杂而不易实现.难以检查逻辑正确性或难以判断分支条件 是否相互交叉或覆盖全面的困扰,此时对这些分支条件包含的 逻辑运算进行简化是一个较好的选择。 卡诺图是电子电路中逻辑运算简化的常用工具,但由于变 量数量限制等局限,未能在软件设计的逻辑简化中得到应用。 根据软件分支条件中常见复杂逻辑的特点,可以经过适当转换 处理后.借助卡诺图工具多个分支条件的逻辑式进行简化,并 判断条件间的交叉和覆盖情况
1软件中常见复杂逻辑判断特点 软件中的逻辑是现实生活中逻辑的映射,常常具有如下特 点:①多个分支逻辑运算并存:满足不同的条件就进入不同的 处理流程;②各分支之间不重叠交叉:一种特定情况对应一个 处理流程,不会出现在一种特定情况下,可以执行两个流程中 的任意一个,或者两个都执行;③复杂逻辑式中的变量可以按 照实际意义关联性进行分组:如果变量很多,这些变量并不是 随机地组合在一起,而是意义相关联的变量之间进行组合的可 能性大。 此类分支逻辑判断的软件实现的理想模式应满足:条件语 句简化易懂,易于检查;各分支条件之间互不交叉,覆盖全面无 遗漏。 下面以笔者完成的一项软件逻辑判断的设计(国家质检总 局464文件企业质量信用分类)为例,进行说明,并以此为例介
卡诺图在“数字逻辑电路”教学中的运用薛俏【摘要】在“数字逻辑电路”教学中,卡诺图的运用广泛而灵活,但对于初学者来说,会认为卡诺图仅是一种化简逻辑函数的工具而已.为使学生正确认识卡诺图,依据“数字逻辑电路”课程的教学特点,结合学生应具有的能力和知识结构,从卡诺图的常规用法和特殊用法两方面探讨了卡诺图在“数字逻辑电路”教学中的运用,为今后的教学起到更好的参考和借鉴作用.【期刊名称】《辽宁科技大学学报》【年(卷),期】2012(035)006【总页数】5页(P618-622)【关键词】卡诺图;数字逻辑电路;竞争冒险;数据选择器【作者】薛俏【作者单位】鞍山技师学院冶金分院,辽宁鞍山 114013【正文语种】中文【中图分类】G642.4;TP331.11953年,美国贝尔实验室的莫里斯·卡诺(Maurice Karnaugh)发明了卡诺图,将逻辑函数真值表中的最小项按矩阵形式排列,并使得此矩阵纵、横方向的逻辑变量取值按格雷码的顺序排列,这样构成的图形就是卡诺图。
卡诺图会使逻辑函数表示更直观,也为逻辑函数化简提供一条思路。
其特点是:(1)卡诺图中的方格总数和逻辑函数的全部最小项数相一致。
(2)在卡诺图中任何两个相邻小方格的最小项只有一个因子不同,而其他因子都相同。
根据其特点可以将“数字逻辑电路”中的逻辑函数用卡诺图的形式来描述,应用于“数字逻辑电路”教学中,能够取得良好的教学效果。
例1 利用卡诺图表示逻辑函数解将逻辑函数表达式变为最小项表达式,并在卡诺图中将表达式中对应的最小项用1表示,其余填0,如图1所示。
即逻辑函数卡诺图上任何2i(i=1,2,…,n)个相邻最小项可以合并为一项,并消除i个变量。
利用这种性质可以对逻辑函数进行化简。
逻辑函数的卡诺图化简步骤:(1)画出逻辑函数的卡诺图。
(2)合并最小项。
以最少的圈,圈最多相邻的1,每个圈内1的个数为2i(i=1,2,…,n)个;最小项可以被重复使用,没有相邻的最小项单独保留。