当前位置：文档之家 › 逻辑代数基础(卡诺图应用及无关项)

逻辑代数基础(卡诺图应用及无关项)

  • 格式：ppt
  • 大小：1.11 MB
  • 文档页数：22

下载文档原格式

  / 22

合集下载

逻辑函数的卡诺图化简PPT课件

逻辑函数的卡诺图化简PPT课件

Digital Logic Circuit
2. 函数为最大项表达式
第5讲 逻辑函数 的卡诺图化简
Digital Logic Circuit
因为相同编号的最小项和最大项之间存在互补关系，所以使函数值 为0的那些最小项的编号与构成函数的最大项表达式中的那些最大项编号 相同，按这些最大项的编号向卡诺图的相应小方格中填上0，其余方格上 填上1即可。
主要项：把2n个为1的相邻最小项进行合并，若卡诺圈不能再扩大，则圈得的合 并与项称为主要项。
必要项：若主要项圈中至少有一个为1的“特定”最小项没有被其它主要项所覆 盖，则称此主要项为必要项或实质主要项。最简逻辑函数中的与项都是必要项。
冗余项：若主要项圈中不包含有为1的“特定”最小项，或者说它所包含为1的最 小项均已被其它的主要项圈所覆盖，则称其为冗余项或多余项。
对于任意的或与表达式，只要当任意一项的或项为0时，函数 的取值就为0。要使或项为0，只须将组成该或项的原变量用0、反 变量用1代入即可。故填写方法是：首先将每个或项的原变量用0、 反变量用1代入，在卡诺图上找出交叉小方格并填写0；然后在其余 小方格上填写1即可。
例4. 作出函数 F ( A, B,C, D) ( A C)(B D)(C D) 对应的卡诺图。
④写出最简的函数表达式。
演示1
演示2
基本步骤图示
第5讲 逻辑函数 的卡诺图化简
逻辑表达式 Y(A,B,C,D)=m(3,5,7,8,11,12,13,15) 或真值表
Digital Logic Circuit
1
卡诺图
1
AB
CD
00 01 11
10
00 0
0
1
1
01 0

利用无关项化简逻辑函数.

利用无关项化简逻辑函数.

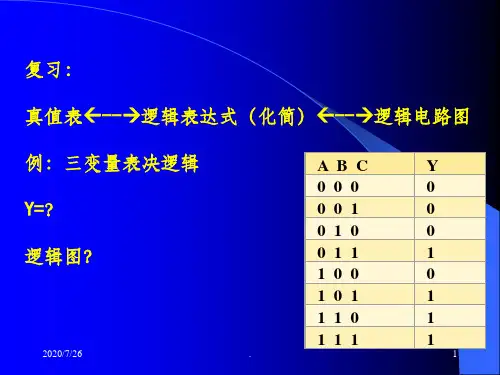
逻辑问题的描述可用真值表、逻辑表达式、逻辑图、卡诺图和时序图，它们各具特点又相互关联。

真值表真值表卡诺图时序图表达式标准式化简变换展开卡诺图填图化简变换一般式逻辑图测试逻辑图
逻辑函数的化简代数化简法：卡诺图化简法：重点填图卡诺图常用编码的卡诺图表示及化简（格雷码、格雷 BCD码、8421码、2421 码、余3码）逻辑函数表达形式化简逻辑函数最简表达形式真值表标准式一般与或式一般或与式其它形式利用无关项进行化简的原则：尽量利用与尽量不用最简与或式最简与非式最简或与式最简或非式最简与或非式
作业7： 2.17（1、3） 2.18（2） 2.20（2） 2.22。

2逻辑代数基础

2逻辑代数基础

（15）
五、德 摩根定理(反演律）：表中8，18 （De Morgan) 证明： 1 AB A B 真值表法、 穷举法 2 A B AB
推广到多变量：
ABC A B C
A B C ABC
说明：两个（或两个以上）变量的与非（或非） 运算等于两个（或两个以上）变量的非或（非 与）运算。
（3）
§2.2
逻辑代数中的三种基本运算
基本逻辑运算：与 ( and )、或 (or ) 、 非 ( not )。 一、“与”逻辑 与逻辑：决定事件发生的各条件中，所有条件都 具备，事件才会发生（成立）。 规定:
A
E
B
C Y
开关合为逻辑“1” 开关断为逻辑“0”
灯亮为逻辑“1”
灯灭为逻辑“0”
（4）
A(BC) A(BC) A B C
注：代入定理还可以扩展其他基本定律 的应用范围！
（23）
2.4.2 反演定理
内容：将函数式F中所有的 + + (反函数) 新表达式： F
变量与常数均取反 显然： F F 规则: 1.遵循先括号 再乘法 后加法的运算顺序。 2.不是一个变量上的反号不动。 用处：实现互补运算（求反运算）。

（29）
2.5.2 逻辑函数的表示方法
真值表：将逻辑函数输入变量取值的不同组合 与所对应的输出变量值用列表的方式 一一对应列出的表格。
四 种 表 示 方 法 n个输入变量
2 种组合。
n
逻辑函数式 (逻辑表示式, 逻辑代数式)
Y AB AB
逻辑图: 波形图
A 1 & ≥1 B 1 &
Y
（30）
Y A B AB AB Y A B AB AB Y A B A B

卡诺图化简法一全文

卡诺图化简法一全文

m0
0
m1如何根据输入1变量组 m2合写出相应最2小项？
m3
3
m4
4
m5
5
m6
6
m7
7
例如 ABC 101 5 m5
m4 4 100 ABC
2. 最小项的基本性质
(1) 对任意一最小项，只有一组变量取值使它的值为1，而
其余各种变量取值均使其值为0。 (2) 不同的最小项，使它的值为1的那组变量取值也不同。 (3) 对于变量的任一组取值，任意两个最小项的乘积为0。 (4) 对于变量的任一组取值，全体最小项的和为1。
每一个与项都是最小项的与或逻辑式称为标 准与或式，又称最小项表达式。
任何形式的逻辑式都可以转化为标准与或式， 而且逻辑函数的标准与或式是唯一的。
[例] 将逻辑式 Y ABC AB C D 化为标准与或式。
解：(1) 利用摩根定律和分配律把逻辑函数式展开为与或式。
Y ABC AB C D ABC AB (C D) ABC ABC ABD 普通与或式，非标准与或式
CD
AB
C D CD CD C D
同一行最 左与最右 AB ABC D ABCD ABCD ABC D
方格相邻
AB ABC D ABCD ABCD ABC D 卡诺图特点： 循环相邻性 AB ABC D ABCD ABCD ABC D
同一列最 上与最下 ቤተ መጻሕፍቲ ባይዱ格相邻
AB ABC D ABCD ABCD ABC D
(2) 找出真值表中Y=1 对应的最小项，在 卡诺图相应方格中 填1，其余不填。
BC A 00 01 11 10
0 10 1 3 12
1 14 5 7 16
已 [例] 已知 Y AD AB(C BD)，试画出Y的卡诺图。 知 解：(1) 将逻辑式转化为与或式

无关项在化简逻辑函数中的应用

无关项在化简逻辑函数中的应用

无关项在化简逻辑函数中的应用
————————————————————————————————作者：————————————————————————————————日期：
无关项在化简逻辑函数中的应用
化简具有无关项的逻辑函数时，如果能合理利用这些无关项，一般都可得到更加简单的化简结果。

为达到此目的，加入的无关项应与函数式中尽可能多的最小项（包含原有的最小项和已写入的无关项）具有逻辑相邻性。

合并最小项时，究竟把卡诺图上的×作为1（即认为函数式中包含了这个最小项）还是作为0（即认为函数式中不包含这个最小项）对待，应以得到的相邻最小项矩形组合最大、而且矩形组合数目最少为原则。

例1：化简逻辑函数
，
给定其约束条件
解：如果不利用约束项，则Y已无可化简。

但适当地加进一些约束项以后，可以得到
利用了约束项以后，使逻辑函数得以进一步化简。

但是代数法表示不够直观。

从逻辑函数的卡诺图上则表示得更清晰。

例2：试化简逻辑函数：
已知其约束条件为：
解：画出函数Y的卡诺图，
于是得到：。

03逻辑代数基础（化简法）.pdf

03逻辑代数基础（化简法）.pdf

讲稿03第1章 逻辑代数基础(逻辑函数的公式法、卡诺图化简法)1.4 逻辑函数的公式化简法 1 . 4 . 1 化简的意义与标准 一、化简逻辑函数的意义二、逻辑函数式的几种常见形式和变换 三、逻辑函数的最简与-或式 1 . 4 . 2 逻辑函数的代数化简法一、并项法 二、吸收法 三、消去法 四、配项法 1 . 4 . 3 代数化简法举例1.4 逻辑涵数的公式化简法 1 . 4 . 1 化简的意义与标准 一、化简逻辑函数的意义根据逻辑问题归纳出来的逻辑函数式往往不是最简逻辑函数式，对逻辑函数进行化简和变换，可以得到最简的逻辑函数式和所需要的形式，设计出最简洁的逻辑电路。

这对于节省元器件，优化生产工艺，降低成本和提高系统的可靠性，提高产品在市场的竞争力是非常重要的。

湖南省高校数字教学资源中心NE </t i t l e ></h e a d ><b o d y ><b r ><b二、逻辑函数式的几种常见形式和变换常见的逻辑式主要有5种形式，如逻辑式可表示为三、逻辑函数的最简与-或式1 . 4 .2 逻辑函数的代数化简法一、并项法湖南省高校数字教学资源中心N E </t it le></h ea d><b od y><b r><b1 . 4 . 3 代数化简法举例在实际化简逻辑函数时，需要灵活运用上述几种方法，才能得到最简与-或式.湖南省高校数字教学资源中心NE </t i t l e ></h e a d ><b o d y ><b r ><b1.5 逻辑函数的卡诺图化简法 1. 5. 1 最小项与卡诺图 一、最小项的定义和性质 1．最小项的定义 2．最小项的基本性质 二、表示最小项的卡诺图 1．相邻最小项2．最小项的卡诺图表示 1. 5. 2 用卡诺图表示逻辑函数 一、逻辑函数的标准与-或式 二、用卡诺图表示逻辑函数1．已知逻辑函数式为标准与-或式，画逻辑函数卡诺图。

逻辑函数的卡诺图化简法

首先讨论三变量（A、B、C）函数卡诺图的画 法。
① 3变量的卡诺图 有23个小方块；
相邻 相邻
② 几何相邻的必须
逻辑相邻：变量的 取值按00、01、11、 10的顺序（循环码 ） 排列 。
图1-11 三变量卡诺图的画法
2021/8/13
11
不 相邻
相邻
相邻
图1-12 四变量卡诺图的画法
正确认识卡诺 图的“逻辑相邻”： 上下相邻，左右相 邻，并呈现“循环 相邻”的特性，它 类似于一个封闭的 球面，如同展开了 的世界地图一样。
A因BB此C是N个三变变量量共函有数2的N个最最小小项项吗。？
2021/8/13
4
最小项的定义:对于N个变量，如果P是一个含有N 个因子的乘积项，而且每一个变量都以原变量或者反 变量的形式，作为一个因子在P中出现且仅出现一次， 那么就称P是这N个变量的一个最小项。
表1-17 三变量最小项真值表
2021/8/13
5
（2）最小项的性质
①对于任意一个最小项，只有一组变量取值使它 的值为1，而变量取其余各组值时，该最小项均为0；
②任意两个不同的最小项之积恒为0； ③变量全部最小项之和恒为1。
2021/8/13
6
最小项也可用“mi” 表示，下标“i”即最小 项的编号。编号方法：把最小项取值为1所对应的 那一组变量取值组合当成二进制数，与其相应的十 进制数，就是该最小项的编号。
ABC ABC AC
(A B)C ABC AC
AC BC ABC AC
（2） 根据与或表达式画出卡诺图，如下
图所示。
2021/8/13
17
BC
A
00 01 11 10
0
11 1

数字逻辑基础卡诺图化简

把每一个乘积项所包含的那些最小项（该乘积项 就是这些最小项的的公因子）所对应的小方块都填上 1，剩下的填0，就可以得到逻辑函数的卡诺图。
例5：已知 YA BA C D A B C D ，画卡诺图。
Y1 AB AB(CC)(DD)
ABCDABCDABCDABCD
m(12,13,14,15)
Y2 AC D A(B B )C D
例3： 已知Y的真值表，要求画Y的卡诺图。
表1-19 逻辑函数Y的真值表
图1-12 例3的卡诺图
ABC
Y
000
0
001
1
010
1
011
0
100
1
101
0
110
0
1 2020/7/26 1 1
1
.
14
练习：三变量表决逻辑真值表填入卡诺图
ABC
Y
000
0
001
0
010
0
011
1
100
0
101
1
110
1
或：Y(A,B,C)m3m6m7
m(3,6,7)
2020/7/26
.
8
例2: 写出三变量函数的最小项表达式。
解 利用摩根定律将函数变换为与或表达式， 然后展开成最小项之和形式。
Y ( A, B, C ) AB AB C AB
AB ABCAB
(A BA B )CA B (CC )
A B C A B C A B C A B C
2020/7/26
.
2
2.4 逻辑函数的卡诺图化简法
公式化简法评价： 优点：变量个数不受限制。 缺点：目前尚无一套完整的方法，结果是否最简 有时不易判断。

卡诺图化简所应用的逻辑代数原理与方法

卡诺图化简所应用的逻辑代数原理与方法kamaugh map Simplification of the applicationof principles and methods of algebraic logic【摘要】逻辑代数卡诺图化简是数字电子技术的一个重要内容，本文讨论了卡诺图化简逻辑代数的化简原理以及基本方法。

卡诺图利用了格雷码的循环相接性质进行化简，采用画卡诺圈进行逻辑合并。

【关键词】逻辑代数；卡诺图；化简【Abstract】Simplifying logic function by kamaugh map is an important content of digital electronic technique. This paper explores the principle and basic methods of Simplifying logic function by kamaugh map.K-map use the cycle phase nature of the Gray code to simplifying logic function and use carnot cycle to merge logic.【Key Word】Logic Function;Karnaugh Map;Simplifying引言在ASIC设计和基于PLD的设计中，最小化都是一个重要的步骤。

多余的门和门输入端需要更多的面积，从而增加了成本。

但是在杂乱的代数符号中找出可结合的项是困难的。

卡诺图是逻辑函数真值表的图形表示，是一种更适于人工操作的最小化方法，其出发点是对真值表进行图形等效，它是通过一种直观形象、易于操作的方式来实现逻辑代数化简。

一、卡诺图化简的相关概念1、最小和：逻辑函数F的最小和是F的一个“积之和”表达式，F的其它“积之和”表达式不会比最小和最小和式中的乘积项更少。

逻辑函数的运算和卡诺图

逻辑函数的最小项表示法，它们具有惟一性。而逻辑表达式和逻辑图 都不是惟一的。使用这些方法时，应当根据具体情况选择最适合的一 种方法表示所研究的逻辑函数。
当前您浏览到是第二十四页，共二十五页。
本章小结
本章介绍了两种逻辑函数化简法。公式化简法是利用逻辑
代数的公式和规则，经过运算，对逻辑表达式进行化简。它的优点是 不受变量个数的限制，但是否能够得到最简的结果，不仅需要熟练地
普通代数结 果如何？
（3）与普通代数相似的定理
交换律 A·B = B·A
A+B=B+A
结合律 A·（B·C）=（A·B）·C A +(B+C)=(A+B)+C
分配律 A·（B+C）=A·B + A·C A+(BC)=(A+B)(A+C)
当前您浏览到是第四页，共二十五页。
（4）特殊的定理
反演律：P14注意
若规定：代表一个最小项的小方格叫做“0”维块。
“0”维块： 表示四个变量一个也没有被消去。
将相邻“0”维块相加，可以将两项合 AB
并为一项，并消去一对因子。
CD 00 01 11 10
相邻项
“0”维块相加“1”维块“2”维“块3”维块00ABmC0D
ABC D
m4
ABCDABC
m12 m8
D
m0+m1 ABC D ABCD ABC
m2 m6 m14 m10
二个“0”维块相加，可合并为一项，并消去一对有 0，1变化因子。 四个“0”维块相加，可合并为一项，并消去二对有 0，1变化因子。
八个“0”维块相加，可合并为一项，并消去三对有 0，1变化因子。
当前您浏览到是第十七页，共二十五页。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

表2.6.1 Y的卡诺图 CD AB 00 01 11 10
00 1 1
×
01 ×
×1
11 × × 1 1 × 1××
2.7.1 约束项、任意项和逻辑函数式中的无关项 还有另一种圈法，如图2.6.2所示
此种圈法圈数少，变量少，
比上一种简单
表2.6.2 Y的卡诺图
CD
简化后的逻辑函数为
AB 00 01 11 10
它们的卡诺图如表2.7.2和 2.7.3所示
BC 表2.7.2 Y的卡诺图 A 00 01 11 10
0
1 11
1
11
则 Y G
BC 表2.7.3 G的卡诺图 A 00 01 11 10
01
11
1
2.7.1.判明函数关系和进行函数的运算
2.函数运算
若已知函数Y1和Y2，则可利用卡诺图做逻辑运算。 例2.7.1若Y1＝AB＋AC ，Y2＝A＋BC 试利用卡诺 图求Y1＋Y2 、Y1＋Y2及Y1⊙Y2
2.7.1 约束项、任意项和逻辑函数式中的无关项
例2.6.1 用卡诺图简化下列逻辑函数，并写成最简与或式 和或与式
Y(A, B,C, D) (0,1,6,9,14,15) d(2,4,7,8,10,11,12,13)
解：Y的卡诺图如表2.6.1所示 则最简与或式为
Y D A BC
Y ABCD ACD ABCD 约束条件：C、D不可能相同
*2.7 卡诺图的其它应用
卡诺图除了简化逻辑函数，还可以有下面的一些应用
2.7.1.判明函数关系和进行函数的运算
1 判明函数关系 利用卡诺图可以判明函数是否相等、互补。若
两个函数的卡诺图相同，则这两个函数一定相等。 即若函数Y和G的卡诺图相同，则Y＝G。若两个函 数的卡诺图中“0”和“1”对调，则这两个函数为互 补。
2.7.1.判明函数关系和进行函数的运算 例如
Y AB AC BC
G AB AC
它们的卡诺图如表 2.7.1所示，则Y＝G
表2.7.1 Y和G的卡诺图 BC
A 00 01 11 10
0
11
1
11
2.7.1.判明函数关系和进行函数的运算
再例如 Y AB C
G AC BC
1. 与或式转换成或与式
已知逻辑函数的与或式，先画出逻辑函数的卡 诺图，再圈“0”，便可得到最简的或与式。
2.7.2 逻辑函数表达式类型的转换
例2.7.2将下面逻辑函数化成最简或与式
Y AB BC AC
解：其卡诺图如表2.7.8 所示
则
BC 表2.7.8 Y的卡诺图 A 00 01 11 10
0
11
11
1
＋
BC 表2.7.5 Y2的卡诺图 A 00 01 11 10
0
1
1 11 1 1
BC 表2.7.7 Y的卡诺图 A 00 01 11 10
=0
11
1 1 11 1
Y Y1 Y2 A B
2.7.1.判明函数关系和进行函数的运算 则两个函数的同或为
表2.7.4 Y1的卡诺图 BC A 00 01 11 10
Y (A C)(A C D)
表2.6.4 Y的卡诺图 CD AB 00 01 11 10
00 × × × ×
01 1 1 0 1 11 × × × × 10 0 0 1 1
2.7.1 约束项、任意项和逻辑函数式中的无关项 练习：将下列函数简化成最简与或式和或与式
Y(A, B,C, D) m(0,1,5,7,8,10,14) d(3,9,11,15) Y(A, B,C, D) m(0,2,7,13,15) d(1,3,4,5,6,8,10)
解： Y1和Y2的卡诺图如表2.7.4及2.7.5所示
表2.7.4 Y1的卡诺图 BC A 00 01 11 10
0
10
0
1
11
1
1 11 1 1
2.7.1.判明函数关系和进行函数的运算 则两个函数的与为
表2.7.4 Y1的卡诺图 BC A 00 01 11 10
0
11
BC 表2.7.5 Y2的卡诺图
A 00 01 11 10
⊙0
1
11
1
1 11 1 1
BC 表2.7.8 Y的卡诺图 A 00 01 11 10
Y Y1 ⊙Y2
= 0 1 11
AC BC AC
11
1
2.7.2 逻辑函数表达式类型的转换
逻辑函数表达式的形式有很多种，如与或式、 或与式、与非式、与或非式等，不同的表达形式可 由不同的门电路来实现。一般的逻辑函数为与或式 （乘积和），这样需要转换成其它的形式，利用卡 诺图可以很方便的实现转换。
0
11
BC 表2.7.5 Y2的卡诺图
. A 00 01 11 10
0
1
11
1
1 11 1 1
BC 表2.7.6 Y的卡诺图
= A 00 01 11 10
0
1
11
1
Y Y1 Y2 AC ABC
2.7.1.判明函数关系和进行函数的运算 则两个函数的或为
表2.7.4 Y1的卡诺图 BC A 00 01 11 10
11 × × 1 1
10 × 1 0 ×
2.7.1 约束项、任意项和逻辑函数式中的无关项
例1.4.13 试简化下列逻辑函数，写最简成与或式和或
与式
Y (A, B,C, D) ABC ABCD ABCD ABCD 约束条件：A⊙ B＝0
解：约束条件为
AB AB 0
00 1 1 0 ×
Y BC BC
01 × 0 × 1
11 × × 1 1 10 × 1 × ×
2.7.1 约束项、任意项和逻辑函数式中的无关项 写成或与式为
Y (B C)(B C)
表2.6.3 Y的卡诺图 CD AB 00 01 11 10
00 1 1 0 ×
01 × 0 × 1
（即AB取值不能相同） 则Y的卡诺图如表2.6.4所示 最简与或式为
CD 表2.6.4 Y的卡诺图 AB 00 01 11 10
00 × × × ×
01 1 1
1
11 × × × ×
Y AC AC CD
10
11
2.7.1 约束项、任意项和逻辑函数式中的无关项
圈“0” 则最简或与式为
Y AB BC AC
0 01 1 1