第四节 线段中点的应用-学而思培优

中点简介中点是数学概念中的一个重要概念，常常用于表示两个点之间的中间位置。

在几何学和代数学中，中点可以用来描述线段或向量的特性。

这篇文档将介绍中点的定义、性质以及在实际应用中的一些例子。

定义在平面几何中，两点A和B之间的中点是通过将线段AB分成两等分的点。

中点被定义为线段的中点，因为它恰好位于线段的中心位置。

假设线段AB的两个端点坐标为A(x1, y1)和B(x2, y2)，那么中点的坐标可以通过如下公式计算得到：($\\frac{x1+x2}{2}$, $\\frac{y1+y2}{2}$)性质中点具有一些重要的性质，下面列出了其中一些常见的性质：1.中点将线段分成两个等长的部分。

换句话说，从A到中点的距离等于从中点到B的距离。

2.中点的横坐标等于线段端点横坐标的平均值，纵坐标也等于线段端点纵坐标的平均值。

3.如果线段AB的中点是M，那么向量AM和向量MB的长度相等，且方向相反。

换句话说，向量AM和向量MB是互为相反向量。

4.中点所在的直线是线段AB的垂直平分线，可以将线段分成两个相等的部分。

应用实例中点在数学中有广泛的应用，下面是一些常见的应用实例：1.在几何学中，中点可以用于构建垂直平分线，帮助解决一些几何问题，比如证明两条线段相等。

2.在物理学中，中点可以用于计算物体的速度。

假设物体在某段时间内从点A到点B移动，我们可以使用点A和点B的坐标来计算出物体的速度向量，其中中点将帮助我们确定物体的位置和速度。

3.在经济学中，中点可以用于计算价格的平均值。

假设有两个价格点A和B，我们可以使用中点来计算这两个价格的平均值，从而了解价格的变化情况。

结论中点是数学中一个重要的概念，用于描述线段或向量的中心位置。

它具有一些特定的性质，如将线段等分、垂直平分线等。

在实际应用中，中点有广泛的应用，包括几何学、物理学和经济学等。

通过理解中点的概念和性质，我们能够在各个领域中更好地应用它，解决问题和提供解决方案。

两点间的距离与线段中点的坐标教学反思在数学中，我们经常会遇到计算两点间的距离和线段中点的坐标的问题。

这些问题在几何学和代数学中都有广泛的应用。

在教学过程中，我注意到学生们对于这些概念和计算方法的理解存在一些困惑。

因此，我决定对这些问题进行反思，并思考如何更好地教授这些内容。

让我们来看看两点间的距离的计算。

对于平面上的两个点A(x1, y1)和B(x2, y2)，我们可以利用勾股定理来计算它们之间的距离。

勾股定理表达了直角三角形斜边的长度与两个直角边长度的关系，即c² = a² + b²。

在这个问题中，我们可以将两点间的距离作为斜边，将x轴和y轴上的距离作为直角边，来应用这个定理。

然而，我发现学生们对于如何应用勾股定理来计算距离存在一些混淆。

他们常常容易忽略平方根的操作，或者将直角边的长度写错。

为了解决这个问题，我引入了一些实际应用例子，帮助学生们理解勾股定理的原理和使用方法。

例如，我给学生们展示了一个直角三角形的例子，其中两个直角边的长度分别为3和4，要求他们计算斜边的长度。

通过这个例子，学生们能够观察到勾股定理的实际应用，并且在计算过程中逐步掌握平方根和平方的操作。

我还引入了一些实际生活中的应用例子，如计算两个城市之间的直线距离、计算直角房间的对角线长度等。

通过将这些抽象的数学概念与实际问题相结合，学生们更容易理解和掌握计算两点间距离的方法。

接下来，让我们来探讨线段中点的坐标的计算。

对于平面上的一条线段AB，线段中点的坐标可以通过以下公式来计算：中点的x坐标为(x1 + x2) / 2，中点的y坐标为(y1 + y2) / 2。

这个公式可以通过将线段的两个端点的x坐标和y坐标相加再除以2来得到。

然而，我发现学生们在计算线段中点坐标时经常出错。

他们容易将x坐标和y坐标分别相加，而忽略了除以2这个步骤。

为了帮助学生们理解和记忆这个公式，我引入了一些图形辅助工具，如坐标轴和图形示意图。

线段的中点定义全文共四篇示例，供读者参考第一篇示例：线段的中点是指连接线段两端点的直线上刚好一分为二的点，也就是位于线段中心的点。

中点是线段的特殊点之一，具有很多性质和应用。

线段的中点可以作为线段的对称轴。

如果以线段的中点为中心，将整个线段进行旋转180度，那么线段就会完美重合，这就意味着线段的中点同时也是线段的对称中心。

这种对称性可以应用于很多几何问题中，例如寻找图形的对称轴，求解对称图形的性质等。

线段的中点可以用来构造含有中垂线的几何问题。

中点和线段上的一个点可以确定一条唯一的中垂线，中垂线是过线段中点且垂直于线段的直线。

利用中点和中垂线的性质，我们可以解决很多有关直角三角形、平行四边形等几何问题。

线段的中点还可以与其他线段的中点结合，形成中线。

中线是连接一个三角形的两个顶点与对边中点的线段，此线段通过三角形的重心点和平行中线两个性质，有助于解决关于三角形的面积、内切圆、外接圆、旁切圆等问题。

由此可见，线段的中点在几何学中具有重要的地位和广泛的应用。

在解决几何问题时，我们经常需要利用线段的中点进行推导和证明。

掌握线段的中点的性质与应用，有助于提高解决几何问题的能力和效率。

线段的中点不仅仅是一条线段上的一个点，更是连接线段两端点的纽带和桥梁，具有丰富的性质和应用价值。

熟练掌握线段的中点的定义与相关性质，能够帮助我们更好地理解和应用几何学知识，为解决几何问题提供重要的线索和思路。

希望大家能够加深对线段中点的认识，充分发挥其在解决几何问题中的作用。

【2000字】第二篇示例：线段的中点是指连接线段两端点的临界点，该点位于线段的中间位置，使得该点到线段两端点的距离相等。

线段的中点在几何学中具有重要的意义，不仅可以帮助我们计算线段的长度，还可以用于找到两个点之间的中心点。

在几何学中，线段是由两个端点所确定的一段直线，它具有一定的长度。

线段的中点是指连接线段两端点的临界点，将线段分成两等长的部分。

线段的中点通常用字符M来表示，如线段AB的中点为M，则可以表示为AM=MB。

线段的中点定义-概述说明以及解释1.引言1.1 概述引言部分将对线段的中点进行定义和探讨。

线段是几何学中的基本概念之一，它是由两个端点之间的所有点组成的一条直线部分。

在几何学中，中点是指线段的一个特殊点，它处于线段的正中间位置，将线段平均分成两个相等的部分。

本文将首先对线段的定义进行阐述，然后探讨中点的定义和性质。

通过对线段和中点的研究，我们可以深入理解线段的特征和属性，进一步应用于几何学中的问题求解和证明过程中。

对于读者来说，了解线段的定义和中点的概念对于几何学的学习和应用非常重要。

通过掌握线段的概念和中点的特性，我们能够更好地理解和解决与线段相关的问题，比如计算线段的长度、判断点是否在线段上等。

在本文的正文部分，我们将详细介绍线段的定义，并进一步探讨中点的性质和特点。

通过实例和证明，我们将演示中点的重要性以及与线段其他部分之间的关系。

最后，在结论部分，我们将对本文进行总结，并展望一些未来研究的方向和可能的应用领域。

希望通过本文的阐述，读者能够对线段的中点有一个清晰的了解，并能够应用于实际问题中。

本文将为读者提供一个基础的概念框架，以便在后续的几何学学习和应用中更好地理解和运用线段的中点概念。

让我们一起开始对线段的中点进行深入研究吧！1.2文章结构文章结构部分的内容可以对整篇文章的组织和框架进行介绍和说明。

下面是一个可能的写作方式：在本文中，我们将详细讨论线段的中点定义。

为了提供给读者一个整体的了解，本文将分为引言、正文和结论三个部分。

首先，在引言部分，我们将概述本文的主题和目的。

我们会简要介绍线段的基本概念，并阐述为什么中点的定义对于理解线段的性质和几何关系非常重要。

其次，在正文部分，我们将深入讨论线段的定义以及中点的概念。

我们会探索一些定义中的关键要素，并解释它们的意义。

我们还将通过几个具体的例子和图示来帮助读者更好地理解中点的概念。

此外，我们还将讨论中点的性质和特点，并与其他相关概念进行比较和对比。

中考数学几何模型4：中点模型名师点睛拨开云雾开门见山中点模型，提到中点，我们需要想到关于中点的以下知识点：①三角形中线平分三角形面积，等分点等分面积；②等腰三角形“三线合一”的性质；③直角三角形斜边上的中线等于斜边的一半；④三角形中位线平行且等于第三边的一半. 这四点使我们已经深入学习过的有关中点运用的知识点，今天重点在结合四点的基础上探究另外一种中点模型，我们简称“平中对模型”，即“平行线+中点+对顶角”构造全等或相似模型，与倍长中线法相通。

ABCDEAB CDEFEDCBA典题探究启迪思维探究重点例题1. 如图，在△ABC的两边AB、AC向形外作正方形ABDE和ACFG，取BE、BC、CG的中点M、Q、N．求证：MQ＝QN．【解答】证明：连接BG和CE交于O，∵四边形ABDE和四边形ACFG是正方形，∴AB＝AE，AC＝AG，∠EAB＝∠GAC，∴∠EAB+∠EAG＝∠GAC+∠EAG，∴∠GAB＝∠EAC，在△BAG和△EAC中，，∴△BAG≌△EAC（SAS），∴BG＝CE．∵BE、BC、CG的中点M、Q、N，∴MQ＝CE，QN＝BG，∵BG＝CE，∴QN＝MQ．变式练习>>>1. 如图，在△ACE中，点B是AC的中点，点D是CE的中点，点M是AE的中点，四边形BCGF和四边形CDHN都是正方形．求证：△FMH是等腰直角三角形．【解答】证明：连接MB、MD，设FM与AC交于点P，∵B、D、M分别是AC、CE、AE的中点，四边形BCGF和四边形CDHN都是正方形，∴MD∥AC，且MD＝AC＝BC＝BF；MB∥CE，且MB＝CE＝CD＝DH，∴四边形BCDM是平行四边形，∴∠CBM＝∠CDM，又∵∠FBP＝∠HDC，∴∠FBM＝∠MDH，在△FBM和△MDH中，∴△FBM≌△MDH（SAS），∴FM＝MH，且∠FMB＝∠MHD，∠BFM＝∠DMH．∴∠FMB+∠HMD＝180°﹣∠FBM，∵BM∥CE，∴∠AMB＝∠E，同理：∠DME＝∠A．∴∠AMB+∠DME＝∠A+∠AMB＝∠CBM，∴∠FMH＝180°﹣（∠AMB+∠DME）﹣（∠FMB+∠HMD）＝180°﹣∠CBM﹣（180°﹣∠FBM）＝∠FBC＝90°，∴△FMH是等腰直角三角形．例题2. 如图，已知BD、CE分别是△ABC的AC、AB边上的高，G、F分别是BC、DE的中点．求证：GF ⊥DE．【解答】证明：如图，连接EG、DG，∵BD、CE分别是△ABC的AC、AB边上的高，点G是BC的中点，∴DG＝EG＝BC，∵点F是DE的中点，∴GF⊥DE．变式练习>>>2. 如图，在△ABC中内取一点，使∠PBA＝∠PCA，作PD⊥AB于点D，PE⊥AC于点E，求证：DE的垂直平分线必过BC的中点M．【解答】解：取BC，PB，PC的中点M，N，F，连接MN，MF，E，DN，DM，EM，∴MF＝BP，MN＝PC，MF∥PN，MN∥PF，∴四边形NMFP是平行四边形，∴∠PNM＝∠PFM，∵PD⊥AB，PE⊥AC，∴DN＝PB，EF＝PC，∴DN＝MF，MN＝EF，∵∠DNP＝2∠ABP，∠PFE＝2∠ACD，∵∠ABP＝∠ACD，∴∠DNP＝∠PFE，∴∠DNM＝∠EFM，在△DNM与△MFE中，，∴△DNM≌△MFE，∴DM＝EM，∴△DME是等腰三角形，∴底边DE的垂直平分线（过M点）必是BC的中点M．例题3. 已知：AD为△ABC的中线，AE是△ABD的中线，AB＝BD，求证：AC＝2AE．（两种证法）【解答】（1）解：∵AD为△ABC的中线，AE是△ABD的中线，∴BD＝CD，BE＝DE，∴BE＝BD，BD＝BC；又∵AB＝BD，∴BE＝AB，AB＝BC，∴＝＝，∠B＝∠B，∴△ABE∽△CBA；（2）证明：∵由（1）知，△ABE∽△CBA，∴＝＝，∴AC＝2AE．变式练习>>>3. 如图①，点O为线段MN的中点，PQ与MN相交于点O，且PM∥NQ，可证△PMO≌△QNO．根据上述结论完成下列探究活动：探究一：如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE＝∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的数量关系，并证明你的结论；探究二：如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC＝1：2，∠BAE＝∠EDF，CF∥AB．若AB＝4，CF＝2，求DF的长度．【解答】解：（1）AB＝AF+CF．如图2，分别延长DC、AE，交于G点，根据图①得△ABE≌△GCE，∴AB＝CG，又AB∥DC，∴∠BAE＝∠G而∠BAE＝∠EAF，∴∠G＝∠EAF，∴AF＝GF，∴AB＝CG＝GF+CF＝AF+CF；（2）如图3，分别延长CF、AE，交于G点，根据CF∥AB得△ABE∽△GCE，∴AB：CG＝BE：CE，而BE：EC＝1：2，AB＝4，∴CG＝8，又AB∥FC，∴∠BAE＝∠G，而∠BAE＝∠EDF，∴∠G＝∠EDF，∴DF＝GF，而CF＝2，∴DF＝CG﹣CF＝8﹣2＝6．例题4. 如图，正方形ABCD和正方形EFCG的边长分别为3和1，点F，G分别在边BC，CD上，P为AE 的中点，连接PG，则PG的长为．【解答】解：方法1、延长GE交AB于点O，作PH⊥OE于点H．则PH∥AB．∵P是AE的中点，∴PH是△AOE的中位线，∴PH＝OA＝（3﹣1）＝1．∵直角△AOE中，∠OAE＝45°，∴△AOE是等腰直角三角形，即OA＝OE＝2，同理△PHE中，HE＝PH＝1．∴HG＝HE+EG＝1+1＝2．∴在Rt△PHG中，PG＝＝＝．故答案是：．变式练习>>>4. 如图，过边长为3的等边△ABC的边AB上一点P，作PE⊥AC于E，Q为BC延长线上一点，当P A＝CQ时，连PQ交AC边于D，则DE的长为．【解答】解：过P作PF∥BC交AC于F，∵PF∥BC，△ABC是等边三角形，∴∠PFD＝∠QCD，∠APF＝∠B＝60°，∠AFP＝∠ACB＝60°，∠A＝60°，∴△APF是等边三角形，∴AP＝PF＝AF，∵PE⊥AC，∴AE＝EF，∵AP＝PF，AP＝CQ，∴PF＝CQ，在△PFD和△QCD中，∴△PFD≌△QCD（AAS），∴FD＝CD，∵AE＝EF，∴EF+FD＝AE+CD，∴AE+CD＝DE＝AC，∵AC＝3，∴DE＝，故答案为．例题5. 如图1，在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG、CG.易证：EG=CG且EG⊥CG.（1）将△BEF绕点B逆时针旋转90°，如图2所示，则线段EG和CG有怎样的数量和位置关系？请直接写出你的猜想.（2）将△BEF绕点B逆时针旋转180°，如图3所示，则线段EG和CG又有怎样的数量和位置关系？请写出你的猜想，并加以证明.（3）将△BEF绕点B旋转一个任意角度α，如图4所示，则线段EG和CG有怎样的数量和位置关系？请直接写出结论.解答：第（1）（2）略（3）解法一：如图，延长EG至点H，使GH=EG.连接DH，CE，CH.因为点G是DF的中点，所以GF=GD.根据SAS易证△GEF≌△GHDEF=HD且∠GEF=∠GHD，所以EF//DH.分别延长HD与EB交于点K，HD的延长线交BC于点M.如下图：因为EB⊥EF，而EF//DH，所以EK⊥HK，即∠BKM=∠MCD=90°.又∠BMK=∠CMD.根据三角形的内角和，可得∠KBM=∠MDC.所以∠EBC=∠HDC.又EB=HD，BC=DC所以△EBC≌△HDC.所以CE=CB且∠ECB=∠HCD.所以∠ECB=90°，即△BCE是等腰直角三角形，又因为点G是斜边EB的中点，所以CG⊥GE且CG=GE.变式练习>>>5. 请阅读下列材料：问题：如图1，在菱形ABCD和菱形BEFG中，点A、B、E在同一条直线上，P是线段DF的中点，连结PG、PC．若∠ABC＝∠BEF＝60°，探究PG与PC的位置关系及数量关系．小聪同学的思路是：延长GP交DC于点H，构造全等三角形，经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）直接写出上面问题中线段PG与PC的位置关系及的值；（2）如图2，在正方形ABCD和正方形BEFG中，点A、B、E在同一条直线上，P是线段DF的中点，连结PG、PC，探究PG与PC的位置关系及数量关系；（3）将图2中的正方形BEFG绕点B顺时针旋转，原问题中的其他条件不变（如图3），你在（2）中得到的两个结论是否发生变化？写出你的猜想并加以证明．【解答】解：（1）PG⊥PC，＝；理由如下：延长GP交DC于H，如图1所示：∵四边形ABCD和BEFG均为菱形，∴DC＝BC，GF＝BG，DC∥AE∥GF，∴∠HDP＝∠GFP，∠DHP＝∠FGP，∵P是线段DF的中点，∴DP＝FP，在△DHP和△FGP中，，∴△DHP≌△FGP（AAS），∴HP＝GP，DH＝FG＝BG，∴CH＝CG，∴CP⊥HG，即PG⊥PC，∵∠ABC═60°，∴∠HCG＝180°﹣60°＝120°，∴∠CGP＝（180°﹣120°）＝30°，∴＝；（3）在（2）中得到的两个结论不发生变化；理由如下：过点F作FH∥DC交CP的延长线于H，交CB的延长线于N，交BE于M，连接CG、HG，如图3所示：则∠CDP＝∠PFH，在△CDP和△FHP中，，∴△CDP≌△FHP（ASA），∴CP＝PH，CD＝FH，∵∠BNM＝∠MEF＝90°，∠BMN＝∠EMF，∴∠NBM＝∠EFM，∵∠CBG+∠NBM＝180°﹣90°＝90°，∠EFM+∠MFG＝90°，∴∠CBG＝∠MFG，在△CBG和△FHG中，，∴△CBG≌△FHG（SAS），∴CG＝GH，∠BGC＝∠FGH，∴∠CGH＝∠BGC﹣∠HGB＝∠FGH﹣∠HGB＝∠BGF＝90°，∴△CGH是等腰直角三角形，∴PG＝PC，且PG⊥PC．达标检测领悟提升强化落实1. 如图所示，M是△ABC的边BC的中点，AN平分∠BAC，BN⊥AN于点N，且AB＝8，MN＝3，则AC的长是（）A．12B．14C．16D．18【解答】解：延长BN交AC于D，在△ANB和△AND中，，∴△ANB≌△AND，∴AD＝AB＝8，BN＝ND，∵M是△ABC的边BC的中点，∴DC＝2MN＝6，∴AC＝AD+CD＝14，故选：B．2. 如图，△ABD和△ACE都是直角三角形，其中∠ABD=∠ACE=90°，且点C在AB上，连接DE，M为DE 中点，连接BM，CM，求证BM=CM.3. 如图，正方形ABCD中，E为CD的中点，F是DA的中点，连接BE，与CF相交于P，求证：AP＝AB．【解答】证明：延长CF、BA交于点M，∵点E、F分别是正方形ABCD的边CD和AD的中点，在△BCE与△CDF中，，∴△BCE≌△CDF（SAS），∴∠CBE＝∠DCF．∵∠DCF+∠BCP＝90°，∴∠CBE+∠BCP＝90°，∴∠BPM＝∠CBE+∠BCP＝90°．在△CDF与△AMF中，，∴△CDF≌△AMF（AAS），∴CD＝AM，∵CD＝AB，∴AB＝AM，∴P A是直角△BPM斜边BM上的中线，∴AP＝BM，即AP＝AB．4. 如图，分别以△ABC的边AB、AC为斜边向外侧构造等腰直角△ABD和等腰直角△ACE，M是BC中点．求证：DM＝ME，DM⊥ME．【解答】证明：如图，取AB、AC的中点F、G，连接DF，MF，EG，MG，∴AF＝，AG＝，∵△ABD和△AEC是等腰直角三角形，∴DF⊥AB，DF＝，EG⊥AC，EG＝，∴∠AFD＝∠AGE＝90°，DF＝AF，GE＝AG．∵M是BC的中点，∴MF∥AC，MG∥AB，∴四边形AFMG是平行四边形，∴AG＝MF，MG＝AF，∠AFM＝∠AGM．∴MF＝GE，DF＝MG，∠AFM+∠AFD＝∠AGM+∠AGE，∴∠DFM＝∠MGE．在△DFM和△MGE中，，∴△DFM≌△MGE（SAS），∴DM＝ME；∠MDF＝∠GME，∵∠MDF+∠BFD+∠BFM+∠DMF＝180°，∠BFD＝90°，∴∠MDF+∠BFM+∠DMF＝90°，∵AB∥MG，∴∠BFM＝∠GMF，∴∠GME+∠GMF+∠DMF＝90°，即∠DME＝90°，∴DM⊥ME．5. 已知△ABC和△ADE是等腰直角三角形，∠ACB＝∠ADE＝90°，点F为BE中点，连接DF、CF．（1）如图1，当点D在AB上，点E在AC上，请判断此时线段DF、CF的数量关系和位置关系，并说明理由．（2）如图2，将△ADE绕点A逆时针旋转45°时，请你判断此时（1）中的结论是否仍然成立？若成立，请证明：若不成立，请说明理由．（3）如图3，将△ADE绕点A逆时针旋转90°时，若AD＝2，AC＝3，求此时△FBC中CF边上的高的长．（直接写出结果）【解答】解：（1）DF＝CF，且DF⊥CF，理由如下：∵∠ACB＝∠ADE＝90°，点F为BE中点，∴∠BDE＝90°，CF＝BE＝EF＝BF，∴DF＝BE＝EF＝BF，∴DF＝CF．∵△ABC和△ADE是等腰直角三角形，∴∠ABC＝45°∵BF＝DF，∴∠DBF＝∠BDF，∵∠DFE＝∠ABE+∠BDF，∴∠DFE＝2∠DBF，同理得：∠CFE＝2∠CBF，∴∠DFE+∠EFC＝2∠DBF+2∠CBF＝2∠ABC＝90°，∴DF＝CF，且DF⊥CF．（2）（1）中的结论仍然成立．理由如下：延长DF交BC于点G．如图2所示：∵∠ADE＝∠ACB＝90°，∴DE∥BC，∴∠DEF＝∠GBF，∠EDF＝∠BGF．∵F为BE中点，∴EF＝BF．在△DEF和△GBF中，∴△DEF≌△GBF（AAS）．∴DE＝GB，DF＝GF．∵AD＝DE，∴AD＝GB，∵AC＝BC，∴AC﹣AD＝BC﹣GB，∴DC＝GC．∵∠ACB＝90°，∴△DCG是等腰直角三角形，∵DF＝GF．∴DF＝CF，DF⊥CF．（3）延长DF交BA于点H，如图3所示：∵△ABC和△ADE是等腰直角三角形，∴AC＝BC，AD＝DE．∴∠AED＝∠ABC＝45°，∵由旋转可以得出，∠CAE＝∠BAD＝90°，∵AE∥BC，∴∠AEB＝∠CBE，∴∠DEF＝∠HBF．∵F是BE的中点，∴EF＝BF，∴△DEF≌△HBF，∴ED＝HB，∵BC＝AC＝3，∠ACB＝90°，∴AB＝AC＝6，∵AD＝2，∴ED＝BH＝2，∴AH＝4，6. 已知：△ABC和△ADE均为等腰直角三角形，∠ABC＝∠ADE＝90°，AB＝BC，AD＝DE，按图1放置，使点E在BC上，取CE的中点F，连接DF、BF．（1）探索DF、BF的数量关系和位置关系，并证明；（2）将图1中△ADE绕A点顺时针旋转45°，再连接CE，取CE的中点F（如图2），问（1）中的结论是否仍然成立？证明你的结论；（3）将图1中△ADE绕A点转动任意角度（旋转角在0°到90°之间），再连接CE，取CE的中点F （如图3），问（1）中的结论是否仍然成立？证明你的结论．【解答】解：（1）DF＝BF且DF⊥BF．（1分）证明：如图1：∵∠ABC＝∠ADE＝90°，AB＝BC，AD＝DE，∴∠CDE＝90°，∠AED＝∠ACB＝45°，∵F为CE的中点，∴DF＝EF＝CF＝BF，∴DF＝BF；（2分）∴∠DFE＝2∠DCF，∠BFE＝2∠BCF，∴∠EFD+∠EFB＝2∠DCB＝90°，即：∠DFB＝90°，∴DF⊥BF．（3分）（2）仍然成立．证明：如图2，延长DF交BC于点G，∵∠ABC＝∠ADE＝90°，∴DE∥BC，∴∠DEF＝∠GCF，又∵EF＝CF，∠DFE＝∠GFC，∴△DEF≌△GCF，∴DE＝CG，DF＝FG，（4分）∵AD＝DE，AB＝BC，∴AD＝CG，∴BD＝BG，（5分）又∵∠ABC＝90°，∴DF＝BF且DF⊥BF．（6分）7. 如图：在△ABC中，AB＝AC，EF交AB于点E，交AC的延长线于点F，交BC于D且BE＝CF，求证：DE＝DF．【解答】证明：如图，过点E作EG∥AC交BC于G，则∠ACB＝∠BGE，∠F＝∠DEG，∵AB＝AC，∴∠B＝∠ACB，∴∠B＝∠BGE，∴BE＝GE，又∵BE＝CF，∴GE＝CF，∵在△CDF和△GDE中，，∴△CDF≌△GDE（AAS），∴DE＝DF．8. （1）已知：如图1，在△ABC中，∠A＝90°，D为BC中点，E为AB上一点，F为AC上一点，ED⊥DF，连接EF，求证：线段BE、FC、EF总能构成一个直角三角形；（2）已知：如图2，∠A＝120°，D为BC中点，E为AB上一点，F为AC上一点，ED⊥DF，连接EF，请你找出一个条件，使线段BE、FC、EF能构成一个等边三角形，给出证明．【解答】（1）证明：延长FD到G使GD＝DF，连接BG，EG，∵D为BC中点，∴BD＝DC，∵在△BDG和△CDF中，，∴△BDG≌△CDF（SAS），∴BG＝FC，∠C＝∠GBD，∵ED⊥DF，∴EG＝EF，∵∠A＝90°，∴∠ABC+∠C＝90°，∴∠ABC+∠GBD＝90°，即∠EBG＝90°，∴线段BE、BG、EG总能构成一个直角三角形，∵BG＝FC，EG＝EF∴线段BE、FC、EF总能构成一个直角三角形；（2）当线段FC＝BE时，线段BE、FC、EF能构成一个等边三角形，证明：延长FD到W使WD＝DF，连接BW，EW，∵D为BC中点，∴BD＝DC，∵在△BDW和△CDF中∴△BDW≌△CDF（SAS），∴BW＝FC，∠C＝∠WBD∵ED⊥DF∴EW＝EF，∵∠A＝120°，∴∠ABC+∠C＝60°，∴∠ABC+∠WBD＝60°，即∠EBW＝60°，∴当线段BW＝BE（或BE＝EW，BW＝WE）时，BE、BW、EW能构成一个等边三角形；∵EW＝EF，BW＝FC∴当线段FC＝BE（或BE＝EF，EF＝FC）时，线段BE、FC、EF能构成一个等边三角形．9. 在Rt△ABC中，D为斜边AB的中点，E，F分别在AC，BC上，∠EDF＝90°，已知CE＝4，AE＝2，BF﹣CF＝，求AB．【解答】解：延长FD至点G，使得DG＝DF，连接AG，EG，EF，如图所示：∵D为斜边AB的中点，∴AD＝BD，在△ADG和△BDF中，，∴∴△ADG≌△BDF（SAS），∴AG＝BF，∠DAG＝∠DBF，∵∠DBF+∠BAC＝90°，∴∠DAG+∠BAC＝90°，即∠EAG＝90°，∴EG2＝AG2+AE2，设BF＝AG＝x，∵BF﹣CF＝，∴CF＝x﹣，∵∠EDF＝90°，∴DE⊥FG，∵DG＝DF，∴EF＝EG，∴EF2＝EG2，在Rt△CEF中，EF2＝CE2+CF2，∴AG2+AE2＝CE2+CF2，即x2+22＝42+（x﹣）2，解得：x＝，∴BF＝，CF＝x﹣＝，∴BC＝BF+CF＝8，∵∠C＝90°，AC＝AE+CE＝6，∴AB＝＝10．10. 在△ABM中，∠ABM＝45°，AM⊥BM，垂足为M，点C是BM延长线上一点，连接AC．（1）如图1，若AB＝3，BC＝5，求AC的长；（2）如图2，点D是线段AM上一点，MD＝MC，点E是△ABC外一点，EC＝AC，连接ED并延长交BC于点F，且点F是线段BC的中点，求证：∠BDF＝∠CEF．【解答】解：（1）∵∠ABM＝45°，AM⊥BM，∴AM＝BM＝AB cos45°＝3×＝3，则CM＝BC﹣BM＝5﹣3＝2，∴AC＝＝＝；（2）延长EF到点G，使得FG＝EF，连接BG．由DM＝MC，∠BMD＝∠AMC，BM＝AM，∴△BMD≌△AMC（SAS），∴AC＝BD，又∵CE＝AC，因此BD＝CE，由BF＝FC，∠BFG＝∠EFC，FG＝FE，∴△BFG≌△CFE，故BG＝CE，∠G＝∠E，所以BD＝CE＝BG，因此∠BDG＝∠G＝∠E．11. （1）方法回顾在学习三角形中位线时，为了探索三角形中位线的性质，思路如下：第一步添加辅助线：如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF＝DE，连接CF；第二步证明△ADE≌△CFE，再证四边形DBCF是平行四边形，从而得到DE∥BC，DE＝BC．（2）问题解决如图2，在正方形ABCD中，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝2，DF＝3，∠GEF＝90°，求GF的长．（3）拓展研究如图3，在四边形ABCD中，∠A＝100°，∠D＝110°，E为AD的中点，G、F分别为AB、CD边上的点，若AG＝4，DF＝，∠GEF＝90°，求GF的长．【解答】解：（1）如图1，在△ABC中，延长DE（D、E分别是AB、AC的中点）到点F，使得EF＝DE，连接CF，在△ADE和△CFE中∵，∴△ADE≌△CFE（SAS），∴AD＝CF，∠A＝∠ECF，∴AD∥CF∵AD＝BD，∴BD＝CF，∵BD∥CF，∴四边形DBCF是平行四边形，∴DE∥BC，DF＝BC∴DE＝DF＝BC．（2）如图2，延长GE、FD交于点H，∵E为AD中点，∴EA＝ED，且∠A＝∠EDH＝90°，在△AEG和△DEH中，，∴△AEG≌△DEH（ASA），∴AG＝HD＝2，EG＝EH，∵∠GEF＝90°，∴EF垂直平分GH，∴GF＝HF＝DH+DF＝2+3＝5；（3）如图3，过点D作AB的平行线交GE的延长线于点H，过H作CD的垂线，垂足为P，连接HF，同（1）可知△AEG≌△DEH，GF＝HF，∴∠A＝∠HDE＝100°，AG＝HD＝4，∵∠ADC＝110°，∴∠HDF＝360°﹣100°﹣110°＝150°，∴∠HDP＝30°，∵∠DPH＝90°∴PH＝2，PD＝2∵DF＝，∴PF＝PD+DF＝+2＝3，在Rt△HFP中，∠HPF＝90°，HP＝2，PF＝3，∴HF＝＝＝，∴GF＝FH＝．12. 在△ABC中，AB＝AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连接BE，点G是BE的中点，连接AG、DG．（1）如图①，当∠BAC＝∠DCF＝90°时，直接写出AG与DG的位置和数量关系；（2）如图②，当∠BAC＝∠DCF＝60°时，试探究AG与DG的位置和数量关系，（3）当∠BAC＝∠DCF＝α时，直接写出AG与DG的数量关系．【解答】（1）AG⊥DG，AG＝DG，证明：延长DG与BC交于H，连接AH、AD，∵四边形CDEF是正方形，∴DE＝DC，DE∥CF，∴∠GBH＝∠GED，∠GHB＝∠GDE，∵G是BE的中点，∴BG＝EG，在△BGH和△EGD中∴△BGH≌△EGD（AAS），∴BH＝ED，HG＝DG，∴BH＝DC，∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵∠DCF＝90°，∴∠DCB＝90°，∴∠ACD＝45°，∴∠ABH＝∠ACD＝45°，在△ABH和△ACD中∴△ABH≌△ACD（SAS），∴∠BAH＝∠CAD，AH＝AD，∵∠BAH+∠HAC＝90°，∴∠CAD+∠HAC＝90°，即∠HAD＝90°，∴AG⊥GD，AG＝GD；（3）DG＝AG tan；证明：延长DG与BC交于H，连接AH、AD，∵四边形CDEF是菱形，∴DE＝DC，DE∥CF，∴∠GBH＝∠GED，∠GHB＝∠GDE，∵G是BE的中点，∴BG＝EG，在△BGH和△EGD中∴△BGH≌△EGD（AAS），∴BH＝ED，HG＝DG，∴BH＝DC，∵AB＝AC，∠BAC＝∠DCF＝α，∴∠ABC＝90°﹣，∠ACD＝90°﹣，∴∠ABC＝∠ACD，在△ABH和△ACD中∴△ABH≌△ACD（SAS），∴∠BAH＝∠CAD，AH＝AD，∴∠BAC＝∠HAD＝α；∴AG⊥HD，∠HAG＝∠DAG＝，∴tan∠DAG＝tan＝，∴DG＝AG tan．。

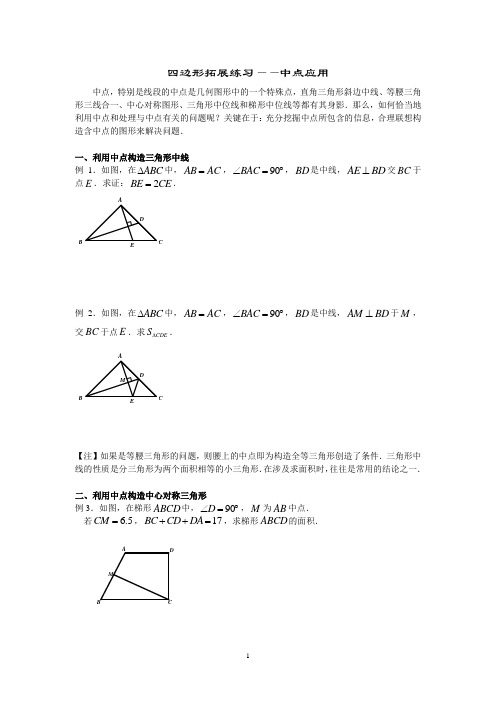
四边形拓展练习——中点应用中点，特别是线段的中点是几何图形中的一个特殊点，直角三角形斜边中线、等腰三角形三线合一、中心对称图形、三角形中位线和梯形中位线等都有其身影．那么，如何恰当地利用中点和处理与中点有关的问题呢？关键在于：充分挖掘中点所包含的信息，合理联想构造含中点的图形来解决问题．一、利用中点构造三角形中线例1．如图，在ABC ∆中，AB AC =，90BAC ∠=︒，BD 是中线，AE BD ⊥交BC 于点E ．求证：2BE CE =．例2．如图，在ABC ∆中，AB AC =，90BAC ∠=︒，BD 是中线，AM BD ⊥于M ，交BC 于点E ．求CDE S ∆．【注】如果是等腰三角形的问题，则腰上的中点即为构造全等三角形创造了条件．三角形中线的性质是分三角形为两个面积相等的小三角形．在涉及求面积时，往往是常用的结论之一．二、利用中点构造中心对称三角形例3．如图，在梯形ABCD 中，90D ∠=︒，M 为AB 中点． 若 6.5CM =，17BC CD DA ++=，求梯形ABCD 的面积．BB例4．如图，在菱形ABCD 中，120ABC ∠=︒，F 是DC 的中点，AF 的延长线交BC 的延长线于点E ．求直线BF 与DE 所夹的锐角的度数．【注】：在四边形问题中，若已知条件中有一边的中点，往往可利用中点构造中心对称的全等的三角形，从而把分散的条件相对集中，为解题创造有利条件．三、利用中点构造三角形中位线例5．如图，在ABC ∆中，7AC =，4BC =，D 为AB 的中点，E 为AC 上一点，且1902AED C ∠=︒+∠．求CE 的长．例6．如图，已知AD 为ABC ∆的角平分线，AB ＜AC ，在AC 上截取CE AB =，M 、N 分别为边BC 、AE 的中点．求证：//MN AD ．【注】：在四边形问题中，当已知条件中出现四边形对边的两个中点时，常见的方法是：另外作对角线的中点，再利用三角形的中位线来解题．EA四、利用中点构造直角三角形斜边中线和三角形中位线例7．如图，在ABC ∆中，AB AC =，AD BC ⊥，垂足为D ，E G 、分别为AD AC 、的中点，DF BE ⊥，垂足为F ．求证：FG DG =．例8．如图，在ABC ∆内取一点P ，使PBA PCA ∠=∠，作PD AB ⊥于点D ，PE AC ⊥于点E ．求证：DE 的垂直平分线必经过BC 的中点M ．【注】：当题目的条件中涉及到三角形一边的中点和直角三角形时，常用的方法是：另取一边（一般取斜边）的中点，为沟通直角三角形斜边中线定理和三角形中位线定理架起一座桥梁．五、利用中点构造梯形中位线例9．在梯形ABCD 中，90ABC DCB ∠=∠=︒，AD 上有一点E 使得BE EC ⊥，且45CED ∠=︒．求证：AB CD BC +=．例10．如图，M N 、分别是四边形ABCD 边AB CD 、的中点，BN 与MC 交于点P ，AN 与MD 交于点Q ．求证：BCP ADQ MQNP S S S ∆∆=+四边形．六、利用多个中点构造三角形和四边形例11．如图，在任意五边形ABCDE 中，M N P Q 、、、分别为AB CD BC DE 、、、的中点，K L 、分别为MN PQ 、的中点．求证：//KL AE 且1=4KL AE ．例12．在六边形ABCDEF 中，//AB DE ，//BC EF ，//CD FA ，AB DE BC EF +=+，1111A B D E 、、、分别是边AB BC DE EF 、、、的中点，且1111A D B E =．求证：CDE AFE ∠=∠．ABE1ADABCD配套练习：1．如图，在菱形ABCD 中，100A ∠=︒，M N 、分别是边AB BC 、的中点，MP CD ⊥于点P ，求NPC ∠的度数．2．如图，在ABC ∆中，D 为边BC 的中点，点E F 、分别在边AC AB 、上，且ABE ACF ∠=∠，BE 与CF 交于点O ，作OP AC ⊥，OQ AB ⊥，P Q 、为垂足．求证：DP DQ =．3．如图，在ABC ∆中，2A B ACB ∠+∠=∠，8BC =，D 为AB 的中点，且CD =，求AC 的长．BBD BAFE MABCDM4．如图，在ABC ∆中，2B C ∠=∠，AD BC ⊥于D ，M 为BC 的中点，求证：12DM AB =5．如图，在ABC ∆中，2ABC C ∠=∠，AD 平分BAC ∠，过BC 的中点M 作AD 的垂线，交AD 的延长线于F ，交AB 的延长线于E ，求证：12BE BD =．6．如图，已知五边形ABCDE 中，90,ABC AED BAC EAD ∠=∠=︒∠=∠。

第一节 与三角形有关的线段一、课标导航二、核心纲要1.三角形的定义：由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2．三角形的分类(1)三角形按边分类3. 三角形的三边关系定理及其应用(1)三角形的三边关系定理：三角形的任意两边之和大于第三边；任意两边之差小于第三边．(2)三角形的三边关系定理的应用①判断给定的三条线段能否围成三角形；②已知两边确定第三边的长或周长的取值范围；③化简代数式；④证明线段间的不等关系．4．三角形的三条重要的线段(1)从三角形的一个顶点向它的对边所在的直线作垂线，顶点和垂足之间的线段叫做三角形的高．(2)连接一个顶点和它所对的边的中点的线段叫做三角形的中线．(3)三角形一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线．5．三线交点位置(1)锐角三角形三条高线的交点在三角形内部，直角三角形三条高线的交点是直角三角形的直角顶点，钝角三角形的三条高所在直线的交点在三角形的外部．交点叫做三角形的垂心．(2)三角形的三条中线都在三角形内部，它们交于一点，且交点在三角形内部．交点叫做三角形的重心．(3)三角形的三条角平分线都在三角形内，并且交于一点，交点叫做三角形的内心．6．三角形具有稳定性7．整数边三角形(1)边长都是整数的三角形称为整数边三角形．(2)若整数a 、b 、c 是三角形的三边，且,c b a ≥≥则⋅++≤<++<≤++30;23C b a c C b a a c b a （当且仅当c b a ==时等号成立）8．数学方法(1)几何问题代数化（转化）．(2)分类讨论．9．几何模型本节重点讲解：一个分类，一个性质（三角形的三边关系），两个方法，两个模型，五个概念（三角形，三角形的高线、中线和角平分线，整数边三角形）．三、全能突破基 础 演 练1．(1)下列各组线段能组成一个三角形的是()．cm cm cm A 6,3,3. cm cm cm B 6,3,2. cm cm cm C 12,8,5. cm cm cm D 11,7,4.(2)下列各组数都表示线段的长度，试判断以这些线段为边能组成三角形的是( )．)3(3,3,.>-a a a A )0(6,4,.>++a a a a B)0,0(,,.>>+b a b a b a C )0(2,1,1.>++a a a a D2．如图11-1-1所示，为估计池塘岸边A 、B 两点的距离，小方在池塘的一侧选取一点0，测得15=OA米，10=OB 米，A 、B 间的距离不可能是( )A.5米 B ．10米 C ．15米 D ．20米3．三角形三条高线的交点恰好是这个三角形的顶点，则这个三角形是( )．A ．锐角三角形B ．直角三角形C ．钝角三角形D ．均有可能4．若一个三角形的两边长分别为5和7，则周长L 的取值范围是若x 为最长边，则x 的取值范围是5．设三角形三边之长分别为3，8，2a -1，则a 的取值范围为6．如图11-1-2所示，一扇窗户打开后，用窗钩BC 可将其固定，这里所运用的几何原理是7．一个等腰三角形的两边长分别为4和5，则它的周长为8．如图11-1-3所示，已知△ABC，按下列要求作图：(1)作△ABC 角平分线AD ；(2)作△ABC 的中线BE ；(3)作△ABC 中AD 边上的高BF ．9．(1)已知a 、b 、c 是△ABC 的三边，且满足,0)()()(222=-+-+-a c c b b a 试判断△ABC 的形状．(2)若△ABC 的三边a 、b 、c 满足,0))()((=---a c c b b a 试判断△ABC 的形状．能 力 提 升10.如图11-1-4所示，在△ABC 中，,BC AD ⊥以AD 为高的三角形有( )个．3.A4.B5.C6.D11．已知a 、b 、c 为△ABC 的三边，化简：||||||b a c a c b c b a -----+-+=12.已知等腰三角形的周长是8，边长为整数，则腰长是13. -个三角形的周长是偶数，其中的两条边是4和2012，则满足上述条件的三角形的个数是 个．14.将长为15cm 的木棒截成长度为整数的三段，使它们构成一个三角形的三边，则不同的截法有种．15.已知五条线段长分别为3、5、7、9、11，若每次以其中三条线段为边组成三角形，则最多可构成互不相同的三角形 个．16．在△ABC 中，AC AC AB ,=上的中线BD 把三角形的周长分为21和12两部分，则三角形各边长为17.如图11-1-5所示，已知△ABC 的三边长均为整数，△ABC 的周长为奇数．(1)若,2,8==BC AC 求AB 的长；(2)若,5=-BC AC 求AB 的最小值；(3)若A （-2，1），B(6，1)，在第一、三象限角平分线上是否存在点P ，使△ABP 的面积为16？若存在，求出P 点坐标；若不存在，请说明理由．18.如图11-1-6所示，一个四边形的四边长分别为,5,4,6,8====AD CD BC AB 它的形状是不稳定的，求AC 和BD 的取值范围．19.如图11-1-7所示，在四边形ABCD 中，对角线AC 、BD 相交于点0，点E 在△ABC 的内部，连接EB ，EC ，说明：;)1(BD AC CD AB +<+;)2(EC EB AC AB +>+(3)若,11,7,6===BC AC AB 求EB+EC 的取值范围．20.已知，点0在△ABC 内部，连接OA 、OB 、OC ，说明：++<++<++AC AB OC OB OA BC AC AB )(21.BC中 考 链 接21.（2011．河北）已知三角形三边长分别为2，？x ，13，若x 为正整数，则这样的三角形的个数为( )．2.A3.B 5.C 13.D22.（2012．杭州）有一组互不全等的三角形，它们的边长均为整数，每个三角形有两条边的长分别为5和7．(1)请写出其中一个三角形的第三边的长；(2)设组中最多有n个三角形，求n的值．巅峰突破23.加油站A和商店B在马路MN的同一侧（如图11-1-8所示），点A到直线MN的距离大于点B到直线MN的距离，AB=7米，一个行人P在马路MN上行走，问：当P到A的距离与P到B的距离之差最大时，这个差等于米．24.不等边△ABC的两条高长度分别为4和12，若第三条高的长也是整数，试求它的长.。

一、中点（中线）的考点①定义：线段相等；②中垂线：定义和性质；③倍长中线法；④等腰三角形三线合一；⑤直角三角形斜边中线定理+2个推论；⑥中位线：多个中点常考中位线；⑦中点坐标公式；⑧平行四边形对角线互相平分；⑨面积平分：过平行四边形对角线交点的直线平分平行四边形的面积；解几何题型1）一定要动手，要动手，要动手！！！（重要的事情说三遍）2）将题目条件转化成数学语言，将“小”的角，线段或面积标在图上；3）根据考点想思路：如看见中点，脑子里蹦出如上知识点和定理；八年级几何题型解题步骤（如：求线段长度）1）设未知数：直接假设所求线段或计算简便的线段；2）把已知“小”的线段或能用未知数表示出来的“小”的线段标在图上；3）找直角三角形（用未知数表示出来的边所在直线三角形）勾股定理列方程；4）求解；5）检验；（类似解应用题的思路）一、中点（中线）的考点定义，性质均为简写，严格定义请翻课本或百度；①定义：线段相等；1．如图，若O是线段AB的中点，则AO=OB；②中垂线：定义和性质；1）定义：垂直线段，平分线段；2）性质1：中垂线上的点到线段两端的距离相等；2．如图，若AO=OB，PO⊥AB，则PA=PB；③倍长中线法（延长加倍法）；3．如图，在△ABC中，点D是BC的中点，AB=6，AC=8，求AD的取值范围；解：延长AD至点E，使得AD=DE，∴AE=2AD，易证△ABD≌△ECD（SAS）,∴CE=AB=6；在△ACE中，2＜AE＜14，∴2＜2AD＜14，即1＜AD＜7；④等腰三角形三线合一；三线合一：等腰三角形顶角的平分线，底边上的中线和底边上的高线互相重合．4．如图，在△ABC中，点D在BC边上，1）AB=AC；2）BD=CD；3）∠BAD=∠CAD；4）AD⊥CD；四个条件中有两个成立，另外两个一定成立（本质是证△ABD≌△ACD）．Ⅰ∵AB=AC，BD=CD；∴∠BAD=∠CAD，AD⊥CD；SSS；SAS；Ⅱ∵AB=AC，∠BAD=∠CAD；∴BD=CD，AD⊥CD；SAS，ASA；Ⅲ∵AB=AC；AD⊥CD；∴BD=CD，∠BAD=∠CAD；HL，AAS；Ⅳ∵BD=CD，∠BAD=∠CAD；∴AB=AC，AD⊥CD；切记SSA不能证≌，故用倍长中线法；Ⅴ∵BD=CD，AD⊥CD；∴AB=AC，∠BAD=∠CAD；SAS；Ⅵ∵∠BAD=∠CAD，AD⊥CD；∴AB=AC，BD=CD；ASA；其中Ⅰ，Ⅳ，Ⅴ与中点有关；⑤直角三角形斜边中线定理+2个推论（比较喜欢说推论好记忆，应是逆命题或逆定理）；定理：直角三角形斜边上的中线等于斜边的一半；5．如图，在△ABC中，点D在AB边上；1）定理：∵∠ACB=90°，AD=DB，∴DA=DB=DC；证明：用倍长中线法构造矩形；延长CD至点E，使得CD=DE，证四边形ACBE是矩形即可；2）推论1：∵∠ACB=90°，DB=DC，∴DA=DB=DC；（同角的余角相等）；证明：∵DB=DC，∴∠DBC=∠DCB，又∠ACB=90°，∴∠DBC+∠A=∠DCB+∠DCA，∴∠A=∠DCA；∴DA=DC，∴DA=DB=DC；3）推论2：∵DA=DB=DC，∴∠ACB=90°；证明：Ⅰ用圆的思想证圆周角∠ACB=90°；Ⅱ∵DA=DC，∴∠A=∠DCA，∵DB=DC，∴∠B=∠DCB，又∠A+∠DCA+∠B+∠DCB=180°；∴∠A+∠B=∠DCA+∠DCB=90°，∴∠ACB=90°；证明方法较多只写常教的方法；⑥中位线：多个中点常考中位线；6．如图，在△ABC中，点D，E分别是AB，AC的中点，则DE∥BC且DE=BC；证明：用倍长中线法构造平行四边形；延长DE至点F，使得DE=EF，连结CF，证△ADE≌△CFE，证四边形DBCF是平行四边形；⑦中点坐标公式；7．在平面直角坐标系中，点A（，），点B（，），点P是线段AB的中点；则；⑧平行四边形对角线互相平分；8．如图，在□ABCD中，AC与BD交于点O，则OA=OC，OB=OD；⑨面积平分：过平行四边形对角线交点的直线平分平行四边形的面积；9．如图，在平面直角坐标系中，□OABC的顶点B的坐标为（15，6），直线恰好将□OABC分成面积相等的两部分，那么b=__________；解：连结OB,AC交于点D则点D（，3）代入直线，得b=；。

学而思倍长中线与截长补短笔记说到“学而思倍长中线与截长补短”这几个词，听起来可能有点复杂吧？别急，咱们今天就来轻松聊聊这些数学概念，把它们讲得通俗易懂，保证你听完之后，能大呼一声：“原来是这么回事！”咱们从“倍长中线”这个词开始讲起。

说白了，它就是指一个三角形中，通过一个顶点，连接到对边中点的那条线段，叫做中线。

你看，三角形有三个顶点，对吧？其中任意一个顶点，如果你连线到对边的中点，这条线就叫做中线。

好了，这条中线有个非常有意思的性质——它的长度是可以通过三角形的边长来“计算”的，也就是说，中线的长度跟三角形的大小、形状有着密切的关系。

如果这条中线很长，那就意味着整个三角形的“体积”或者说“尺寸”也很大。

嗯，这种情况下，你就可以直观地感觉到，三角形不可能很“瘦”，一定得是那种相对“厚实”的存在。

听起来是不是有点抽象？其实挺简单的！想象一下，如果你拿着尺子量一量，中线越长，三角形就越“胖”对吧？这不就很容易理解了吗？接下来咱们再说“截长补短”这个词。

其实啊，这个就很形象了。

你看，生活中咱们常说“强中自有强中手”对吧？意思就是做任何事儿都有更厉害的人。

那数学里也一样，所谓“截长补短”就是通过调整和补充某些不足的部分来弥补短板，达到一个平衡的效果。

怎么说呢？如果你在一个三角形里看到有一条边特别长，而另一条边特别短，这时候你就可以通过“截长补短”的方式，把那些不平衡的地方调整过来，最终让三角形的各个边长都差不多，看上去更加和谐。

这个方法其实特别像咱们生活中的一些调整，比如当你发现自己某一方面的能力差了点，你是不是就会去加强那一部分，反过来让自己更加全面？“截长补短”不就这么回事吗？它就是利用“强”的去弥补“弱”的，让整体看起来更加完美。

这两者之间其实有很多相似之处。

比如“倍长中线”给人的感觉就是一种“加长”的状态，想象一下，那个中线如果特别长，三角形就会变得庞大。

而“截长补短”则是一种“调整”的方式，把过长的部分调整到适当的长度，然后补充短缺的地方。