2019-2020学年九年级数学上册 第22章 二次函数复习学案(新版)新人教版.doc

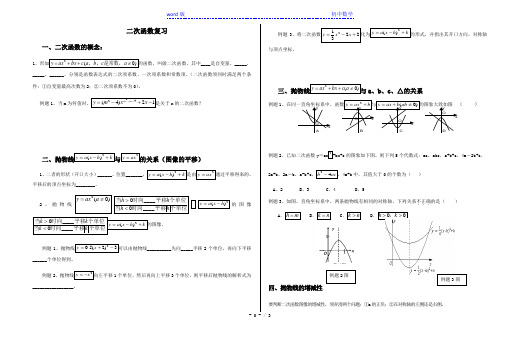
二次函数复习一、二次函数的概念：1、形如)0(2≠++=a c b a c bx ax y 是常数，、、的函数，叫做二次函数。

其中____是自变量，_____，_____，______，分别是函数表达式的二次项系数、一次项系数和常数项。

（二次函数须同时满足两个条件：①自变量最高次数为2；②二次项系数不为0）。

例题1、当m 为何值时，12)4(422-+-=--x xm y m m 是关于x 的二次函数？二、抛物线k h x a y +-=2)(与2ax y =的关系（图像的平移）1、二者的形状（开口大小）______，位置_______，k h x a y +-=2)(是由2ax y =通过平移得来的，平移后的顶点坐标为________。

2、抛物线)0(2≠=a ax y 个单位平移时向当个单位平移时向当h h h h ____0____0<>2)(h x a y -=的图像个单位平移时向当个单位平移时向当k k k k ____0____0<>k h x a y +-=2)(的图像。

例题1、抛物线3)2(5.02-+=x y 可以由抛物线__________先向_____平移2个单位，再向下平移______个单位得到。

例题2、抛物线2x y -=向左平移1个单位，然后再向上平移3个单位，则平移后抛物线的解析式为_________________。

例题3、将二次函数22312+-=x x y 化为k h x a y +-=2)(的形式，并指出其开口方向、对称轴与顶点坐标。

三、抛物线)0(2≠++=a c bx ax y 与a 、b 、c 、△的关系 例题1、在同一直角坐标系中，函数b ax y +=2与)0(≠+=ab b ax y 的图象大致如图 （ ）例题2、已知二次函数y ＝ax 2+bx+c 的图象如下图。

则下列5个代数式：ac ，abc ，a+b+c ，4a －2b+c ，2a+b ，2a －b ，a-b+c ，ac b 42-，4a+b 中，其值大于0的个数为（ ） A 、2 B 、3 C 、4 D 、5例题3、如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确．．．的是（ ） A ．h m = B ．k n = C ．k n > D ．00h k >>，四、抛物线的增减性要判断二次函数图像的增减性，须弄清两个问题：①a 的正负；②在对称轴的左侧还是右侧。

第22章二次函数期末复习课
教学目标：
知识与技能：
理解二次函数的概念，掌握二次函数y＝ax2+bx+c(a≠0)的图象与性质；会用描点法画抛物线，能确定抛物线的顶点、对称轴、开口方向，能较熟练地由抛物线y＝ax2(a≠0)经过适当平移得到y＝a(x－h)2＋k(a≠0)的图象。

会结合二次函数的图象分析问题、解决问题，并在运用中体会二次函数的实际意义，会运用二次函数求实际问题中的最大值或是最小值。

过程与方法：
会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质。

情感态度价值观：
使学生体会数学建模思想，函数思想，数形结合思想等数学思想。

教学的重点：
1.用配方法求二次函数的顶点，对称轴，根据图象概括二次函数的性质。

2.二次函数三种解析式的求法。

3.利用二次函数的知识解决数学问题，并对解决问题的方法进行反思。

教学的难点：1.将实际问题转化为二次函数，并运用二次函数性质将以解决。

2.二次函数与一元二次方程、不等式的联系，数形结合思想的渗透于应用。

3. 运用二次函数知识解决综合性的问题。

教法方法：自主学习法合作学习法
教学手段：多媒体
教学课时：1课时
教学活动：学生活动及设计意图
；⑤若抛物线顶点坐
教学活动：学生活动及设计意图
=x+b的图象交
教学活动：学生活动及设计意图
7.已知抛物线y=ax2+bx和直线y=ax+b在同一坐标系内的图象
如图，其中正确的是（）
专题三：二次函数解析式的确定
求下列二次函数解析式：（学生分组完成）
1.已知二次函数的图象的顶点坐标为（－2，－3），。

人教版九年级上册数学二次函数小结与复习 学案（1）【复习目标】1．理解二次函数的概念，掌握二次函数y ＝ax 2的图象与性质；2．会用描点法画抛物线，能确定抛物线的顶点、对称轴、开口方向，能较熟练地由抛物线y ＝ax2经过适当平移得到y ＝a(x －h)2＋k 的图象。

【学习过程】:一、自主与指导练习1．二次函数的概念，二次函数y ＝ax 2(a ≠0)的图象性质。

例：已知函数4m m2x )2m (y-++=是关于x 的二次函数，求：(1)满足条件的m 值；(2)m 为何值时，抛物线有最低点?求出这个最低点．这时当x 为何值时，y 随x 的增大而增大? (3)m 为何值时，函数有最大值?最大值是什么?这时当x 为何值时，y 随x 的增大而减小?注意：二次函数的一般式为y ＝ax 2＋bx ＋c(a ≠0)。

强调a ≠0．而常数b 、c 可以为0，当b ，c 同时为0时，抛物线为y ＝ax 2(a ≠0)。

此时，抛物线顶点为(0，0)，对称轴是y 轴，即直线x ＝0。

、2．用配方法求抛物线的顶点，对称轴；抛物线的画法，平移规律。

例：用配方法求出抛物线y ＝－3x 2－6x ＋8的顶点坐标、对称轴，并画出函数图象，说明通过怎样的平移，可得到抛物线y ＝－3x 2。

注意：抛物线的一般式与顶点式的互化关系： y ＝ax 2＋bx ＋c ——→ y ＝a(x ＋b 2a )2＋4ac －b24a利用抛物线的对称性进行画图，先确定抛物线的顶点、对称轴，利用对称性列表、描点、连线。

抛物线的平移抓住关键点顶点的移动。

3．知识点串联，综合应用。

例：如图，已知直线AB 经过x 轴上的点A(2，0)，且与抛物线y ＝ax 2相交于B 、C 两点，已知B 点坐标为(1，1)。

(1)求直线和抛物线的解析式；(2)如果D 为抛物线上一点，使得△AOD 与△OBC 的面积相等，求D 点坐标。

巩固练习：1、某公司的生产利润原来是a 元，经过连续两年的增长达到了y 万元，如果每年增长的百分数都是x ，那么y 与x 的函数关系是（ ）A ．y=a （1－x ）2；B ．y=x 2+a 2； C ．y= a （x －1）； D ．y ＝a （l+x ）2、抛物线y=－12 （x －2）2－1经y=－12x 2平移得到（ ）A ．向左平移2个单位，向上平移1个单位；；B ．向右平移2个单位，向上平移1个单位C ．向右平移2个单位，向下平移1个单位D ．向左平移2个单位，向下平移1个单位3. 二次函数 y=-2（x －3）2+5的图象的开口方向、对称轴和顶点坐标分别为（ ）A ．向下，对称轴x=－3，顶点坐标为(3,5)B ．向下，对称轴x ＝3，顶点坐标为(3，5)C ．向上,对称轴x=－3,顶点坐标为(－3,5)D ．向上,对称轴x=－3,顶点坐标为(－3,－5）4. 设直线 y=2x —3，抛物线 y=x 2－2x ，点P （1，－1），那么点P （1，－1）（ ） A ．既在直线上，又在抛物线上； B ．既不在直线上，又不在抛物线上 C ．在直线上，但不在抛物线上； D ．在抛物线上，但不在直线上 5. 函数2y ax bx c =++的图象图1所示，那么关于x 的方程230ax bx c ++-= 的根的情况是（ ）A ．有两个相等实数根；B ．有两个异号实数根；C ．有两个不相等的实数根；D ．无实数根6．不论m 为何实数，抛物线y=x 2－mx ＋m －2的图象（ ）A ．在x 轴上方；B ．与x 轴只有一个交点；C ．与x 轴有两个交点；D ．在x 轴下方7．已知二次函数21y ax bx c =++（a ≠0）与一次函数2y kx m =+（k ≠0）的图象交于点A （－2，4），B （8，2），如图所示，则能使12y y >成立的x 的 取值范围是（ ）A.2x <-B. 28x -<<C. 8x >D.2x <-或8x > 8. 直线2y x =+与抛物线22y x x =+的交点坐标为 。

第22章二次函数教学时间课题《二次函数》小结与复习（2）课型新授课教学目标知识和能力会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质，能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。

过程和方法情感态度价值观教学重点用待定系数法求函数的解析式、运用配方法确定二次函数的特征。

教学难点会运用二次函数知识解决有关综合问题。

教学准备教师多媒体课件学生“五个一”课堂教学程序设计设计意图一、例题精析，强化练习，剖析知识点用待定系数法确定二次函数解析式．例：根据下列条件，求出二次函数的解析式。

(1)抛物线y＝ax2＋bx＋c经过点(0，1)，(1，3)，(－1，1)三点。

(2)抛物线顶点P(－1，－8)，且过点A(0，－6)。

(3)已知二次函数y＝ax2＋bx＋c的图象过(3，0)，(2，－3)两点，并且以x＝1为对称轴。

(4)已知二次函数y＝ax2＋bx＋c的图象经过一次函数y＝－3/2x＋3的图象与x轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)2＋k的形式。

学生活动：学生小组讨论，并让学生阐述解题方法。

教师归纳：二次函数解析式常用的有三种形式： (1)一般式：y＝ax2＋bx＋c (a≠0)(2)顶点式：y＝a(x－h)2＋k (a≠0) (3)两根式：y＝a(x－x1)(x－x2) (a≠0)当已知抛物线上任意三点时，通常设为一般式y＝ax2＋bx＋c形式。

当已知抛物线的顶点与抛物线上另一点时，通常设为顶点式y＝a(x－h)2＋k形式。

当已知抛物线与x轴的交点或交点横坐标时，通常设为两根式y＝a(x－x1)(x－x2)强化练习：已知二次函数的图象过点A(1，0)和B(2，1)，且与y轴交点纵坐标为m。

(1)若m为定值，求此二次函数的解析式；(2)若二次函数的图象与x轴还有异于点A的另一个交点，求m的取值范围。

二、知识点串联，综合应用例：如图，抛物线y＝ax2＋bx＋c过点A(－1，0)，且经过直线y＝x－3与坐标轴的两个交点B、C。

二次函数教学时间课题《二次函数》小结与复习（2）课型新授课教学目标知识和能力会用待定系数法求二次函数的解析式，能结合二次函数的图象掌握二次函数的性质，能较熟练地利用函数的性质解决函数与圆、三角形、四边形以及方程等知识相结合的综合题。

过程和方法情感态度价值观教学重点用待定系数法求函数的解析式、运用配方法确定二次函数的特征。

教学难点会运用二次函数知识解决有关综合问题。

教学准备教师多媒体课件学生“五个一”课堂教学程序设计设计意图一、例题精析，强化练习，剖析知识点用待定系数法确定二次函数解析式．例：根据下列条件，求出二次函数的解析式。

(1)抛物线y＝ax2＋bx＋c经过点(0，1)，(1，3)，(－1，1)三点。

(2)抛物线顶点P(－1，－8)，且过点A(0，－6)。

(3)已知二次函数y＝ax2＋bx＋c的图象过(3，0)，(2，－3)两点，并且以x＝1为对称轴。

(4)已知二次函数y＝ax2＋bx＋c的图象经过一次函数y＝－3/2x＋3的图象与x轴、y轴的交点；且过(1，1)，求这个二次函数解析式，并把它化为y＝a(x－h)2＋k的形式。

学生活动：学生小组讨论，并让学生阐述解题方法。

教师归纳：二次函数解析式常用的有三种形式： (1)一般式：y＝ax2＋bx＋c (a≠0)(2)顶点式：y＝a(x－h)2＋k (a≠0) (3)两根式：y＝a(x－x1)(x－x2) (a≠0)当已知抛物线上任意三点时，通常设为一般式y＝ax2＋bx＋c形式。

当已知抛物线的顶点与抛物线上另一点时，通常设为顶点式y＝a(x－h)2＋k形式。

当已知抛物线与x轴的交点或交点横坐标时，通常设为两根式y＝a(x－x1)(x－x2)强化练习：已知二次函数的图象过点A(1，0)和B(2，1)，且与y轴交点纵坐标为m。

(1)若m为定值，求此二次函数的解析式；(2)若二次函数的图象与x轴还有异于点A的另一个交点，求m的取值范围。

二、知识点串联，综合应用例：如图，抛物线y＝ax2＋bx＋c过点A(－1，0)，且经过直线y＝x－3与坐标轴的两个交点B、C。

人教版九年级数学上册第22章二次函数《复习课》导学案第二十二章复课1.知道二次函数的概念、图象和性质,能根据解析式判断抛物线的开口方向、对称轴、顶点坐标和函数的增减性.2.知道抛物线与对应的一元二次方程的关系,会用待定系数法求二次函数的解析式.3.能够运用二次函数解决一些实际问题,从中体会数学建模思想.4.重点:二次函数解析式的求法,二次函数的图象、性质和应用.◆体系构建◆核心梳理1.一般地,形如y=ax2+bx+c(a,b,c是常数,a≠0)的函数,叫做二次函数.其中x是自变量,a,b,c分别是函数解析式的二次项系数、一次项系数和常数项.2.二次函数y=ax2+bx+c(a≠0)与一元二次方程的关系:(1)当b2-4ac>时,抛物线与x轴有2个交点,对应的一元二次方程有两个不相等的实数解;(2)当b2-4ac=时,抛物线与x轴有1个交点,对应的一元二次方程有两个相等的实数解;(3)当b2-4ac<时,抛物线与x轴无交点,对应的一元二次方程无实数解.3.填表:特征函数启齿偏向对称轴极点坐标(0,0)(0,k)(h,0)(h,k)最值最小值最大值最小值k最大值k最小值最大值最小值k最大值k最小值y=ax2y=ax2+ky=a(x-h)2y=a(x-h)2+k a>时启齿向上a<时开口向下a>时开口向上a<时启齿向下a>时启齿向上a<时启齿向下a>时开口向上a<时开口向下a>时启齿向上y轴y轴x=hx=hy=ax2+bx+ca<时开口向下x=-(-,)最大值专题一:二次函数的概念、图象和性质1.二次函数y=ax2+bx+c的图象如图所示,那么abc,b2-4ac,2a+b,a+b+c这四个代数式中,值为正数的有(B)A.4个B.3个C.2个D.1个2.二次函数y=ax2+bx+c与一次函数y=ax+c在同一坐标系中的图象可能是(C)3.如图,已知二次函数y 1=ax2+bx+c与一次函数y2=kx+m的图象相交于A(-2,4),B(8,2),则能使y1>y2成立的x的取值范围是x<-2或x>8.【方法归纳交流】根据抛物线的开口方向判断a的正负;根据抛物线与y轴的交点判断c的值;若抛物线的对称轴在y 轴左侧,则a与b同号,若抛物线的对称轴在y轴右侧,则a与b异号;根据抛物线与x轴交点的个数判断b2-4ac的符号.专题二:求抛物线的顶点和对称轴4.求抛物线y=x2-4x+5的开口方向、对称轴及顶点坐标.(用两种方法)解:(1)y=(x2-8x+10)=[(x2-8x+16)-16+10]=(x-4)2-3,所以抛物线的开口向上,对称轴是x=4,顶点坐标是(4,-3).(2)对称轴:x=-=4,y最小==-3,顶点坐标为(4,-3).【方法归纳交流】求抛物线的顶点和对称轴一般有两种方法:配方法和公式法.专题三:抛物线的平移5.申明抛物线y=-3x2-6x+8通过如何的平移,可获得抛物线y=-3x2.解:配方:y=-3x2-6x+8=-3(x2+2x-)=-3[(x2+2x+1)-1-]=-3(x+1)2+11,∴抛物线的顶点坐标是(-1,11),∴把抛物线y=-3x2-6x+8先向右平移1个单位长度,再向下平移11个单位长度得到y=-3x2.6.如图,抛物线y=ax2-5ax+4a与x轴相交于点A、B,且过点C(5,4).(1)求a的值和该抛物线顶点P的坐标;(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的解析式.解:(1)把C(5,4)代入y=ax2-5ax+4a,得25a-25a+4a=4。

第 1 页 共 2 页 第 2页 共2页二次函数复习一、二次函数的概念：1、形如)0(2≠++=a c b a c bx ax y 是常数，、、的函数，叫做二次函数。

其中____是自变量，_____，_____，______，分别是函数表达式的二次项系数、一次项系数和常数项。

（二次函数须同时满足两个条件：①自变量最高次数为2；②二次项系数不为0）。

例题1、当m 为何值时，12)4(422-+-=--x xm y m m 是关于x 的二次函数？二、抛物线k h x a y +-=2)(与2ax y =的关系（图像的平移）1、二者的形状（开口大小）______，位置_______，k h x a y +-=2)(是由2ax y =通过平移得来的，平移后的顶点坐标为________。

2、抛物线)0(2≠=a ax y 个单位平移时向当个单位平移时向当h h h h ____0____0<>2)(h x a y -=的图像个单位平移时向当个单位平移时向当k k k k ____0____0<>k h x a y +-=2)(的图像。

例题1、抛物线3)2(5.02-+=x y 可以由抛物线__________先向_____平移2个单位，再向下平移______个单位得到。

例题2、抛物线2x y -=向左平移1个单位，然后再向上平移3个单位，则平移后抛物线的解析式为_________________。

例题3、将二次函数22312+-=x x y 化为k h x a y +-=2)(的形式，并指出其开口方向、对称轴与顶点坐标。

三、抛物线)0(2≠++=a c bx ax y 与a 、b 、c 、△的关系例题1、在同一直角坐标系中，函数b ax y +=2与)0(≠+=ab b ax y 的图象大致如图 （ ）例题2、已知二次函数y ＝ax 2+bx+c 的图象如下图。

则下列5个代数式：ac ，abc ，a+b+c ，4a －2b+c ， 2a+b ，2a －b ，a-b+c ，ac b 42-，4a+b 中，其值大于0的个数为（ ）A 、2B 、3C 、4D 、5例题3、如图，直角坐标系中，两条抛物线有相同的对称轴，下列关系不正确．．．的是（ ） A ．h m = B ．k n = C ．k n > D ．00h k >>，四、抛物线的增减性要判断二次函数图像的增减性，须弄清两个问题：①a 的正负；②在对称轴的左侧还是右侧。

《第22章 二次函数》复习学案 NO ：24班级_______姓名_________小组_______评价_______一、复习目标1、理解二次函数的概念、三种形式的解析式，掌握二次函数的图象与性质；2、历经二次函数的图象与性质的探索过程，领会数形结合的思想并能运用解决实际问题；3、极度热情投入，高效参与学习。

二、自主复习（知识点清理）1、形如_________________(_______)的函数叫做二次函数；其中a 、b 、c 分别叫做__________，____________，_________。

2、二次函数解析式的三种形式：（1）一般式y=ax 2+bx+c(a≠0)，（2）顶点式y=a(x-h)2+k(a≠0)，(3) 两根式y=a(x-x 1)(x-x 2) (a≠0)。

3、二次函数的图象与性质：二次函数的图象都是一条曲线，叫做_________。

（1）y=ax 2(a≠0)：①顶点坐标是________，②对称轴是________，③当a ＞0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大，④当a ＜0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大。

（2）y=ax 2+k (a≠0)：①顶点坐标是________，②对称轴是________，③当a ＞0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大，④当a ＜0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大。

（3）y=a(x-h)2+k(a≠0)：①顶点坐标是________，②对称轴是________，③当a ＞0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大，④当a ＜0，开口向______，此时，x___时，y 随x 的增大而减小，x___时，y 随x 的增大而增大。