基础数学实验示例

第1篇一、实验目的本次实验旨在让学生掌握数学建模的基本步骤，学会运用数学知识分析和解决实际问题。

通过本次实验，培养学生主动探索、努力进取的学风，增强学生的应用意识和创新能力，为今后从事科研工作打下初步的基础。

二、实验内容本次实验选取了一道实际问题进行建模与分析，具体如下：题目：某公司想用全行业的销售额作为自变量来预测公司的销售量。

表中给出了1977—1981年公司的销售额和行业销售额的分季度数据（单位：百万元）。

1. 数据准备：将数据整理成表格形式，并输入到计算机中。

2. 数据分析：观察数据分布情况，初步判断是否适合使用线性回归模型进行拟合。

3. 模型建立：利用统计软件（如MATLAB、SPSS等）进行线性回归分析，建立公司销售额对全行业的回归模型。

4. 模型检验：对模型进行检验，包括残差分析、DW检验等，以判断模型的拟合效果。

5. 结果分析：分析模型的拟合效果，并对公司销售量的预测进行评估。

三、实验步骤1. 数据准备将数据整理成表格形式，包括年份、季度、公司销售额和行业销售额。

将数据输入到计算机中，为后续分析做准备。

2. 数据分析观察数据分布情况，绘制散点图，初步判断是否适合使用线性回归模型进行拟合。

3. 模型建立利用统计软件进行线性回归分析，建立公司销售额对全行业的回归模型。

具体步骤如下：（1）选择合适的统计软件，如MATLAB。

（2）输入数据，进行数据预处理。

（3）编写线性回归分析程序，计算回归系数。

（4）输出回归系数、截距等参数。

4. 模型检验对模型进行检验，包括残差分析、DW检验等。

（1）残差分析：计算残差，绘制残差图，观察残差的分布情况。

（2）DW检验：计算DW值，判断随机误差项是否存在自相关性。

5. 结果分析分析模型的拟合效果，并对公司销售量的预测进行评估。

四、实验结果与分析1. 数据分析通过绘制散点图，观察数据分布情况，初步判断数据适合使用线性回归模型进行拟合。

2. 模型建立利用MATLAB进行线性回归分析，得到回归模型如下：公司销售额 = 0.9656 行业销售额 + 0.01143. 模型检验（1）残差分析：绘制残差图，观察残差的分布情况，发现残差基本呈随机分布，说明模型拟合效果较好。

八皇后实验报告八皇后实验报告引言：八皇后问题是一个经典的数学问题，它要求在一个8x8的国际象棋棋盘上放置8个皇后，使得任意两个皇后都不会互相攻击。

这个问题看似简单，但实际上却充满了挑战。

在本次实验中，我们将探索八皇后问题的解法，并通过编写算法来解决这个问题。

一、问题背景：八皇后问题最早由数学家马克斯·贝瑟尔于1848年提出，它是一道经典的递归问题。

在国际象棋中，皇后可以在同一行、同一列或同一对角线上进行攻击，因此我们需要找到一种方法，使得8个皇后彼此之间不会相互攻击。

二、解决方法：为了解决八皇后问题，我们可以使用回溯法。

回溯法是一种穷举搜索的方法，它通过逐步尝试所有可能的解决方案，直到找到符合要求的解。

具体步骤如下：1. 初始化一个8x8的棋盘，并将所有格子标记为无皇后。

2. 从第一行开始，依次尝试在每一列放置一个皇后。

3. 在每一列中，检查当前位置是否符合要求，即与已放置的皇后不在同一行、同一列或同一对角线上。

4. 如果当前位置符合要求，将皇后放置在该位置，并进入下一行。

5. 如果当前位置不符合要求，尝试在下一列放置皇后。

6. 重复步骤3-5，直到找到一个解或者所有可能的位置都已尝试过。

7. 如果找到一个解，将其输出；否则，回溯到上一行，继续尝试下一列的位置。

三、编写算法：基于上述步骤，我们可以编写一个递归函数来解决八皇后问题。

伪代码如下所示：```function solveQueens(board, row):if row == 8:print(board) # 打印解returnfor col in range(8):if isSafe(board, row, col):board[row][col] = 1solveQueens(board, row + 1)board[row][col] = 0function isSafe(board, row, col):for i in range(row):if board[i][col] == 1:return Falseif col - (row - i) >= 0 and board[i][col - (row - i)] == 1:return Falseif col + (row - i) < 8 and board[i][col + (row - i)] == 1:return Falsereturn Trueboard = [[0]*8 for _ in range(8)]solveQueens(board, 0)```四、实验结果：通过运行上述算法，我们得到了八皇后问题的所有解。

数学实验典型案例
数学实验典型案例有很多，以下是一些例子：
1. 随机数的生成：通过实验理解随机数的生成原理，以及随机数在概率统计中的应用。

可以使用编程语言（如Python）生成随机数，并通过多次实验计算概率等统计指标。

2. 几何图形的绘制：通过几何软件（如GeoGebra）绘制各种几何图形，观察图形的性质和变化规律。

例如，绘制函数图像、探究图形的对称性、研究图形的面积和体积等。

3. 微积分的可视化：使用数学软件（如Matlab、Mathematica）可视化微积分中的概念，如极限、导数、积分等。

通过观察图形的变化，理解微积分的本质和意义。

4. 矩阵运算的实验：通过编程语言进行矩阵的加法、减法、乘法、逆矩阵等运算，理解矩阵运算的基本性质和实际应用。

5. 概率统计的模拟实验：通过模拟实验理解概率统计中的概念和原理，例如通过抛硬币实验计算概率、通过模拟实验估计参数等。

这些案例只是数学实验的一小部分，实际上还有很多其他有趣和实用的数学实验等待探索。

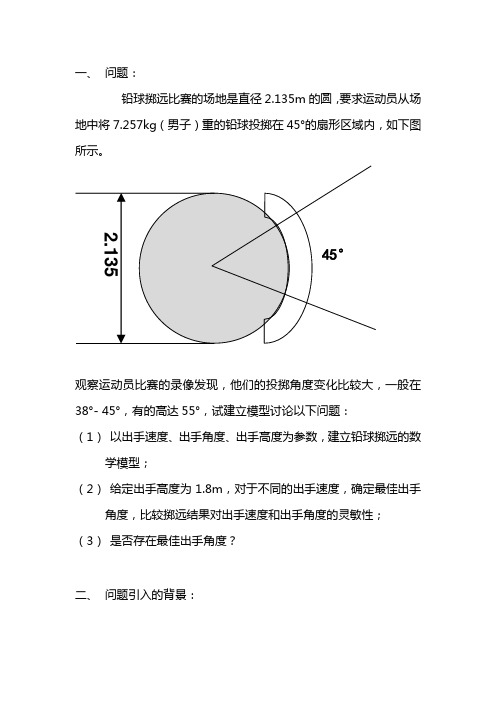
一、问题：铅球掷远比赛的场地是直径2.135m的圆，要求运动员从场地中将7.257kg（男子）重的铅球投掷在45°的扇形区域内，如下图所示。

观察运动员比赛的录像发现，他们的投掷角度变化比较大，一般在38°- 45°，有的高达55°，试建立模型讨论以下问题：（1）以出手速度、出手角度、出手高度为参数，建立铅球掷远的数学模型；（2）给定出手高度为1.8m，对于不同的出手速度，确定最佳出手角度，比较掷远结果对出手速度和出手角度的灵敏性；（3）是否存在最佳出手角度？二、问题引入的背景：铅球比赛是奥运会中一项重要的比赛项目，在铅球比赛中，运动员在投掷圈中站立开始投掷。

投掷圈外围是金属镶边，有6毫米厚，顶端涂白。

投掷时，运动员不能接触铁边的顶端或者投掷圈以外的地面，铅球的投掷圈直径2.135米。

圈内地面由水泥或者有相似的硬度又能防滑的物质构成，它的高度略低于地面高度。

铅球投掷圈的正前方放着一个木质的抵趾板，用来防止运动员滑出圈外。

运动员可以碰抵趾板的内侧，但不能碰抵趾板的顶部。

运动员进入圈内开始投掷后，如果运动员身体的任何部位触及圈外地面，或触及铁圈和抵趾板上面，或以不符合规定的方式将铅球推出，均判为一次试掷失败。

铅球必须完全落在落地区角度线内沿以内，试掷方为有效。

每次有效试掷后，应立即测量成绩。

从铅球落地痕迹的最近点取直线量至投掷圈内沿，测量线应通过投掷圈圆心。

运动员在器械落地后方可离开投掷圈。

离开投掷圈时首先触及的铁圈上沿或圈外地面必须完全在圈外白线的后面，白线后沿的延长线应能通过投掷圈圆心。

铅球的投掷运动是运动员单手托住7.264kg(16磅)重的铅球在直径为2.135m的投掷圆内将铅球掷出并且使铅球落入开角为45°的有效扇形区域内。

以铅球的落地点与投掷圆间的距离度量铅球投掷的远度，并以铅球投掷远度的大小评定运动员的成绩。

在铅球的训练和比赛中，铅球投掷距离的远与近是人们最关心的问题。

初中数学实验教学案例实验教学在初中数学教学中扮演着重要的角色，它通过实际操作与观察，培养学生的实践能力和科学精神，提高学生对数学知识的理解和应用能力。

本文将以探究式学习为例，介绍一种中学数学实验教学案例。

一、背景介绍在初中数学教学中，实验教学可以通过让学生亲自进行实验操作，提供具体的问题背景和操作指导，让学生自主探索和发现数学规律。

这种教学方法有助于培养学生的观察能力和逻辑思维能力。

二、实验目标本次实验的目标是帮助学生理解大数和小数的概念，以及它们在实际生活中的应用。

通过实际测量和对比，学生应能够准确理解数的大小和数的位值。

三、实验步骤1. 准备工作：老师准备一些小球和一个精确的天平，将小球分别装入三个透明容器，其中一个容器装有一百个小球，一个装有十个小球，一个装有一个小球。

2. 实验探索：学生拿起容器逐一称量，观察并记录读数。

3. 实验总结：学生根据观察结果，总结大数和小数的特点，并与老师和同学进行交流讨论。

4. 概念巩固：在实验的基础上，老师进一步引导学生对大数和小数的排列顺序进行理解和记忆，并通过示例让学生理解数的位值概念。

四、教学重点通过实验的方式，帮助学生理解大数和小数的概念，掌握数的比较和排列顺序，巩固数的位值概念。

五、实验的教学意义1. 培养学生的观察能力和实践能力：通过实际操作，学生能够亲身体验数的大小和数的位值，培养学生的观察能力和实践能力。

2. 提高学生对数学概念的理解和应用：通过实验，学生能够更加深入地理解大数和小数的概念，并能够将其应用到实际问题中。

3. 培养学生的科学精神：实验教学能够培养学生的科学精神，让他们通过自主探究和发现，培养独立思考和问题解决的能力。

六、实验结果分析通过实验测量和观察，学生应能够明确地发现，小数指的是比1小的数，大数指的是比100大的数。

他们还应该能够发现，数的位值决定了数的大小。

七、部分学生的思考和总结一些学生会思考为什么个位上的数比十位上的数大，一些学生还会思考什么是无限小数。

数学实验之学生实验题目 MATLAB 简介实验一：数组操作及运算练习1．设有分块矩阵⎥⎦⎤⎢⎣⎡=⨯⨯⨯⨯22322333S O R E A ，其中E,R,O,S 分别为单位阵、随机阵、零阵和对角阵，试通过数值计算验证⎥⎦⎤⎢⎣⎡+=22S 0RS R EA 。

2．求如下非齐次线性方程组的通解，⎪⎩⎪⎨⎧=--+=+-+=+-+.12,2224,12w z y x w z y x w z y x3．某零售店有9种商品的单件进价（元）、售价（元）及一周的销量下表，问哪种商品的利润最大，哪种商品的利润最小；按收入由小到大，列出所有商品及其收入；求这一周该10种商品的总收入和总利润。

实验二：作图练习1. 用两种方法在同一个坐标下作出y 1= x 2,y 2= x 3,y 3= x 4 y 4= x 5这四条曲线的图形，并要求用两种方法在图上加各种标注。

2．用subplot 分别在不同的坐标系下作出下列四条曲线，为每幅图形加上标题， 1）概率曲线 2exy -=；2）四叶玫瑰线 r =sin2q ；3）叶形线 ⎪⎪⎩⎪⎪⎨⎧+=+=;13,13323t ty t t x 4）曳物线 22111lnyyy x --±= 。

3．作出下列曲面的3维图形，1）)sin(22y x z +=π；2）环面：⎪⎩⎪⎨⎧=+=+=,sin ,sin )cos 1(,cos )cos 1(u z v u y v u x )2,0()2,0(ππ∈∈v u 。

实验三：编写M-文件1．建立一个命令M-文件：求所有的“水仙花数”，所谓“水仙花数”是指一个三位数，其各位数字的立方和等于该数本身。

例如，153是一个水仙花数，因为153=13+53+33。

2．编写函数M-文件SQRT.m ：用迭代法求a x =的值。

求平方根的迭代公式为迭代的终止条件为前后两次求出的x 的差的绝对值小于10-5。

〈返回〉方程求解实验一：油价与船速的优化问题油价的上涨，将影响大型海船确定合理的航行速度，以优化航行收入。

数学游戏数10的科学实验在数学教学中，我们常常使用游戏来激发学生的兴趣，提高他们对数学的理解和应用能力。

本文将介绍一个有趣的数学游戏，通过这个游戏，学生可以进行科学实验，并且在实践中体验与数10相关的数学概念。

实验材料：1. 一组标有数字1至9的扑克牌；2. 遮盖物（如纸板或幕布）；3. 记分板和记分笔（可选）。

实验步骤：1. 将扑克牌洗混后，平均分为两堆，每堆牌面向下放置在桌面上；2. 每个玩家轮流翻开一张扑克牌，将其牌面向上展示；3. 两位玩家根据翻出的数字，计算相应数字与10的差值；4. 若计算结果为正数，则将其记录在记分板上；若计算结果为负数，则不记录；5. 玩家依次翻开剩下的扑克牌，执行步骤3和步骤4；6. 计算每位玩家的得分，得分最高的玩家获胜。

实验原理：通过进行这个数学游戏，孩子们可以锻炼他们的心算能力，并加深他们对数学中正负数的理解。

该游戏旨在通过计算给定数字与10的差值来提高孩子们的计算能力和注意力。

此外，游戏的竞争性也能激发孩子们的学习兴趣，并培养他们的团队合作精神。

实验结果：根据孩子们的实验结果，可以分析他们的计算能力和对正负数的理解程度。

高得分的孩子通常能够快速、准确地计算给定数字与10的差值，表明他们在数学方面有较好的基础，对正负数的概念有较深入的理解。

而低得分的孩子可能需要加强对基础数学概念的学习和掌握。

实验拓展：在这个数学游戏的基础上，我们还可以引入其他的数学概念，例如加减法、乘除法等。

通过逐步引入更复杂的计算规则，可以帮助孩子们巩固和扩展他们的数学知识。

此外，可以将游戏规则进行改编，加入更多的变量和挑战，以提高孩子们的数学逻辑思维和问题解决能力。

结论：通过进行这个有趣的数学游戏，我们可以让孩子们在娱乐中学习，培养他们的数学兴趣、注意力和计算能力。

这种科学实验式的教学方法可以更好地激发学生的学习动力，提高他们对数学的兴趣和理解。

希望通过这种创新的教学方式，可以帮助孩子们更轻松地掌握数学知识，并在数学学习中取得更好的成绩。

《数学实验》实验报告１x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02]];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25}];Show[t1,t2]首先得到a，b，c三个值： {{a->27.56,b->-0.0574286,c->0.000285714}}然后得到同一坐标系下的数据点散点图及拟合函数的图形：试验过程（含详细试验步骤、程序清单及异常情况记录等）输入以下mathematica语句求解参数a,b,c:运行后可得解：２为求得数据点的散点图及拟合函数的图形，输入以下语句，并将两个图画在同一坐标下：运行得：３在最开始时，我输入的程序是这样的：x=Table[10.0+5.0*i,{i,0,4}];y={27.0,26.8,26.5,26.3,26.1};xy=Table[{x[[i]],y[[i]]},{i,1,5}];q[a_,b_,c_] :=Sum[(a+b*x[[i]]+c*x[[i]]^2-y[[i]])^2,{i,1,5}]NSolve[{D[q[a,b,c],a]==0, D[q[a,b,c],b]==0,D[q[a,b,c],c]==0},{a,b,c}]t1=ListPlot[xy,PlotStyle->PointSize[0.02],DisplayFunction->Identity];f[x_] :=27.56+ -0.0574286*x+0.000285714*x^2;t2=Plot[f[x],{x,5,35},AxesOrigin->{5,25},DisplayFunction->Identity];Show[t1,t2, DisplayFunction->$ DisplayFunction]然而得到的结果没有图形（如下）：我比照了老师的讲义，改动了“DisplayFunction->Identity”，可是，结果还是一样，没有图形。

数学实验典型案例全文共四篇示例，供读者参考第一篇示例：数学实验是数学教学中不可或缺的一环，通过实验，学生可以更直观地认识数学知识，培养解决问题的能力和逻辑思维。

下面我们来看一些典型的数学实验案例，帮助学生更好地理解和掌握数学知识。

实验一：用三角形拼图探究三角形的性质这个实验旨在帮助学生探究三角形的性质。

教师让学生用拼图拼出不同形状的三角形，然后让学生观察三角形的属性，包括边长、角度、高度等。

通过观察和比较，学生可以发现不同的三角形之间的关系，了解三角形的性质和特点。

实验二：使用平衡秤探究平行线的性质这个实验旨在帮助学生探究平行线的性质。

教师可以准备一个平衡秤和一些不同长度的直线，让学生用平行线的方法来使平衡秤保持平衡。

通过实验，学生可以探究平行线的性质，包括同位角、内错角和同旁内角等。

这样可以让学生更深入地理解平行线的性质。

实验三：用图形和模型探究体积和表面积的关系这个实验旨在帮助学生探究体积和表面积的关系。

教师可以准备一些不同形状的图形和模型，让学生通过测量和计算来探究它们的体积和表面积之间的关系。

通过实验，学生可以发现不同形状的图形和模型之间的体积和表面积的规律，从而更好地理解这两个概念。

通过上述的数学实验案例，我们可以看到，数学实验是帮助学生深入理解和掌握数学知识的重要手段。

教师可以通过设计各种有趣的实验，激发学生的学习兴趣，培养学生的探究能力和解决问题的能力。

希望学生能够通过数学实验，更好地理解和运用数学知识，为未来的学习和生活打下坚实的基础。

【字数达到最低要求】第二篇示例：数学实验典型案例具有重要意义，不仅可以帮助学生巩固所学知识，还可以让他们通过实践探索数学规律，培养解决问题的能力。

下面将介绍几个经典的数学实验案例:一、随机实验与概率计算随机实验是概率论中的基本概念，通过实验可以帮助学生理解随机事件发生的规律。

可以进行抛硬币实验，记录正反面的次数，计算出正反面出现的概率分布；或者进行色子实验，统计各种点数出现的频率，从而了解点数的概率分布。

小学生数学实验100例第1篇：我的数学小实验的日记今天中午，为了能把筷子体积测得更准确，我叫爸爸从化学室拿了一个细长的量筒，刻度单位更小，每个单位只有1立方厘米。

此时，我似乎感觉到了胜利在向我招手，真可谓万事具备，只差动手实验了。

首先，我用铅笔在一次筷子上划了一道分界线，将筷子平均分成两段，并用水浸泡，以免筷子在测定过程中洗水。

随后，将筷子入量筒中，并用滴管将水滴入量筒中，让量筒内的水涨到筷子的分界线上，记下量筒内的水位刻度（38毫升）后，将筷子从量筒内取出，再记下量筒内的水位刻度（34.5毫升），前后两次水位刻度之差就是这一部分筷子的体积，即3.5立方厘米。

用同样的方法，我又测量了筷子另一部分的体积是5立方厘米，两次测定结果相加得到这双筷子的体积为8.5立方厘米。

当我得到这个结果时，我兴奋地叫了，此时的我是多么自豪、多么骄傲啊！接着，我又按每人一天使用3双计算出了我们学校（1500人）及全国（12亿）一年消耗的一次*筷子量，分别是13.96立方米和11169000立方米。

结果使我大吃一惊，每年竟有这么多的木料做成一次筷子被浪费了，真是太可惜！在此，我呼吁在校的同学，不！是全国，也不！应该是全世界的每个人都不要再使用一次筷子了，只有这样，才能保护好我们的森林资源，使我们共有的地球环境更加美好，让地球上的每一个人呼吸到干净、清新的空气。

第2篇：我的小实验数学日记下午放学时，班主任老师给我们布置了一道家庭作业，要求大家想办法测算一次筷子的体积，并用数学日记的形式将测算过程记录下来。

这道家庭作业，表面上是一次数学实践活动，实际可能寓意更深，因为一次筷子的使用与环保有关，一回到家，我就静静地坐在书桌前思考这个问题。

一次*筷子的形状是一个不规则的立体图形，怎样才能测算出它的体积呢?我思来想去，一会儿抓耳挠腮，一会儿摇，终于，有了一点眉目。

我可以将一次筷子放入装满水的容器中，这样容器中的水就会溢出来，溢出水的多少不就是筷子的体积吗?可是筷子比水轻，会浮在水面上，又该怎么办呢?可不可以用石头或胶布之类的东西将筷子固定住呢?我想应该是可以的，但这些办法测定起来又都太麻烦了，要是有更简便的方法该多好啊!经过冥思苦想，我终于自豪的笑了。