数学实验实验报告记录概率与频率

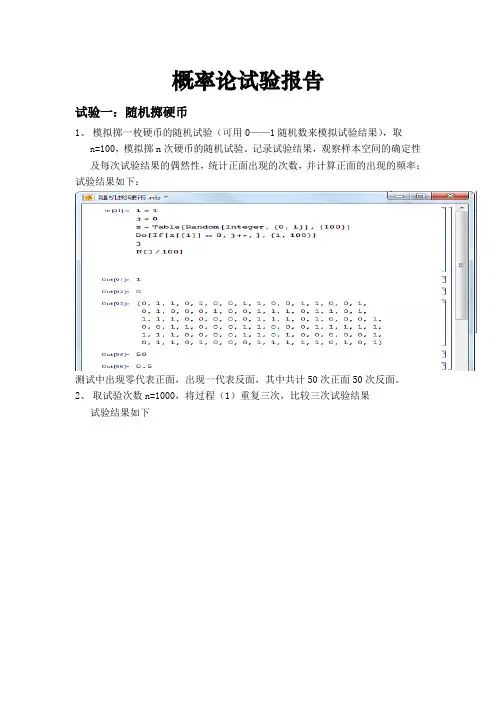
概率论试验报告试验一：随机掷硬币1、模拟掷一枚硬币的随机试验（可用0——1随机数来模拟试验结果），取n=100，模拟掷n次硬币的随机试验。

记录试验结果，观察样本空间的确定性及每次试验结果的偶然性，统计正面出现的次数，并计算正面的出现的频率；试验结果如下：测试中出现零代表正面，出现一代表反面，其中共计50次正面50次反面。

2、取试验次数n=1000，将过程（1）重复三次，比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。

这充分说明模拟情况接近真实情况，频率接近概率0.5。

试验二：高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中，当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知，这是一个经典的古典概型试验问题2、具体程序：3、我们分析实验结果可知，若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。

,5.0试验三：抽签试验1、我们做模拟实验，用1-10的随机整数来模拟实验结果。

在1-10十个随机数中，假设10代表抽到大王，将这十个数进行全排，10出现在哪个位置，就代表该位置上的人摸到大王。

每次随机排列1-10共10个数，10所在的位置随机变化，分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。

概率论与数理统计实验报告概率论部分实验二《正态分布综合实验》实验名称：正态分布综合实验实验目的：通过本次实验，了解Matlab在概率与数理统计领域的应用，学会用matlab做概率密度曲线，概率分布曲线，直方图，累计百分比曲线等简单应用；同时加深对正态分布的认识，以更好得应用之。

实验内容：实验分析：本次实验主要需要运用一些matlab函数，如正态分布随机数发生器normrnd函数、绘制直方图函数hist函数、正态分布密度函数图形绘制函数normpdf函数、正态分布分步函数图形绘制函数normcdf等；同时，考虑到本次实验重复性明显，如，分别生成100,1000,10000个服从正态分布的随机数，进行相同的实验操作，故通过数组和循环可以简化整个实验的操作流程，因此，本次实验程序中要设置数组和循环变量。

实验过程：1.直方图与累计百分比曲线1）实验程序m=[100,1000,10000]; 产生随机数的个数n=[2,1,0.5]; 组距for j=1:3for k=1:3x=normrnd(6,1,m(j),1); 生成期望为6，方差为1的m(j)个正态分布随机数a=min(x); a为生成随机数的最小值b=max(x); b为生成随机数的最大值c=(b-a)/n(k); c为按n(k)组距应该分成的组数 subplot(1,2,1); 图形窗口分两份hist(x,c);xlabel('频数分布图'); 在第一份里绘制频数直方图yy=hist(x,c)/1000; yy为各个分组的频率s=[];s(1)=yy(1);for i=2:length(yy)s(i)=s(i-1)+yy(i);end s[]数组存储累计百分比x=linspace(a,b,c);subplot(1,2,2); 在第二个图形位置绘制累计百分比曲线plot(x,s,x,s);xlabel('累积百分比曲线');grid on; 加网格figure; 另行开辟图形窗口，为下一个循环做准备endend2）实验结论及过程截图实验结果以图像形式展示，以下分别为产生100,1000,10000个正态分布随机数，组距分别为2,1,0.5的频数分布直方图和累积百分比曲线，从实验结果看来，随着产生随机数的数目增多，组距减小，累计直方图逐渐逼近正态分布密度函数图像，累计百分比逐渐逼近正态分布分布函数图像。

第1篇一、引言概率论与数理统计是研究随机现象的数学分支，频率估计概率是概率论中一个重要的实践问题。

通过对大量样本的观察，我们可以估计出某一事件发生的概率。

本实践报告旨在通过实际操作，验证频率估计概率的方法，并分析其有效性和局限性。

二、实践目的1. 理解频率估计概率的基本原理。

2. 掌握使用频率估计概率的方法。

3. 分析频率估计概率的有效性和局限性。

4. 培养实际操作能力和数据分析能力。

三、实践方法本次实践采用以下方法进行频率估计概率：1. 数据收集：从实际生活或实验中收集大量样本数据。

2. 数据整理：对收集到的数据进行清洗、分类和整理。

3. 频率计算：计算每个事件发生的频率。

4. 概率估计：根据频率估计每个事件发生的概率。

5. 结果分析：分析频率估计概率的有效性和局限性。

四、实践过程1. 数据收集本次实践选择了一个简单的例子：抛掷一枚硬币100次，记录正面朝上的次数。

2. 数据整理将收集到的数据记录在表格中，如下所示：| 抛掷次数 | 正面朝上次数 || -------- | ------------ || 100 | 52 |3. 频率计算计算正面朝上的频率：52/100 = 0.52。

4. 概率估计根据频率估计正面朝上的概率为0.52。

5. 结果分析通过实际操作，我们得到了正面朝上的概率估计值为0.52。

与理论值（0.5）相比，存在一定的误差。

这可能是由于样本量较小，或者实验过程中存在一定的随机性。

五、实践结果1. 频率估计概率的有效性：通过本次实践，我们发现频率估计概率是一种有效的方法。

在一定条件下，频率估计的概率值可以近似反映事件的真实概率。

2. 频率估计概率的局限性：频率估计概率存在一定的局限性。

首先，样本量的大小对估计结果的准确性有重要影响。

样本量越大，估计结果越接近真实值。

其次，实验过程中可能存在随机性，导致估计结果与真实值存在偏差。

六、结论频率估计概率是概率论与数理统计中一个重要的实践问题。

高中概率数学实验报告实验目的通过进行概率实验，加深对概率理论的理解，探究概率实验和理论概率的关系。

实验器材- 骰子- 纸牌- 两个硬币实验步骤1. 首先，我们进行了一个简单的抛硬币实验。

通过抛两个硬币，我们观察到硬币的正反面朝上的情况，并记录下来。

共进行了100次抛硬币实验。

2. 接着，我们进行了掷骰子实验。

我们使用一个六面骰子，进行了300次掷骰子实验。

记录下了每次出现的骰子点数。

3. 最后，我们进行了一次纸牌实验。

我们使用了一副标准的扑克牌，包括52张牌，不计大小王。

我们从中抽取了30张牌，记录下了每张牌的花色和点数。

结果分析抛硬币实验我们进行了100次抛硬币实验，记录下了每次抛硬币的结果。

通过统计，我们发现正面朝上的次数为56次，反面朝上的次数为44次。

根据统计学原理，我们得出正面和反面朝上的概率分别为0.56和0.44。

实验结果与理论概率相差较小，这说明我们的实验结果与理论概率一致，加深了我们对硬币抛掷的概率理解。

掷骰子实验我们进行了300次掷骰子实验，记录下了每次点数的结果。

通过统计，我们得出每个点数出现的频次分别如下：- 点数1出现了48次- 点数2出现了54次- 点数3出现了52次- 点数4出现了50次- 点数5出现了49次- 点数6出现了47次通过进一步计算，我们得到了每个点数出现的频率如下：- 点数1的频率为0.16- 点数2的频率为0.18- 点数3的频率为0.17- 点数4的频率为0.16- 点数5的频率为0.16- 点数6的频率为0.15与理论概率进行对比发现，实验结果与理论概率也符合得较好，加深了我们对骰子点数的概率理解。

纸牌实验我们从一副标准扑克牌中抽取了30张牌，记录下了每张牌的花色和点数。

通过统计，我们得出了每个花色和点数出现的频次。

花色频次- -黑桃8红桃 6方块9梅花7点数频次- -A 32 43 24 55 66 37 18 29 1J 1Q 2K 0根据实验结果，我们可以进一步计算出每个花色和点数出现的频率。

大学概率统计实验报告引言在概率统计学中，实验是一种重要的数据收集方法。

通过实验，我们可以收集到一系列随机变量的观测值，然后利用统计方法对这些观测值进行分析和推断。

本实验旨在通过一个简单的骰子实验来介绍概率统计的基本理论和方法。

实验目标本实验的目标是通过投掷骰子的实验，验证骰子的随机性，并研究骰子的概率分布。

实验步骤1.准备一个六面骰子和一张记录表格。

2.将骰子投掷20次，并记录每次投掷的结果。

将结果按照出现的次数填入表格中。

3.统计记录表格中每个数字出现的频数，并计算频率。

4.绘制柱状图展示各个数字的频率分布情况。

实验结果与分析根据实验记录表格，我们统计得到了每个数字出现的频数如下：数字 1 2 3 4 5 6频数 4 3 6 2 4 1根据频数，我们可以计算出每个数字的频率。

频率是指某个数字出现的次数与总次数的比值。

通过计算，我们得到了每个数字的频率如下：数字 1 2 3 4 5 6频率0.2 0.15 0.3 0.1 0.2 0.05通过绘制柱状图，我们可以更直观地观察到各个数字的频率分布情况。

柱状图如下所示：0.3 | █| █| █| █0.25 | █| █| █| █0.2 | █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.15 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.1 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.05 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █----------------1 2 3 4 5 6根据实验结果，我们可以观察到以下现象和结论： - 各个数字的频率接近于理论概率，表明骰子的结果具有一定的随机性。

- 数字3的频率最高，约为0.3，而数字6的频率最低，约为0.05。

这说明骰子的结果并不完全均匀，存在一定的偏差。

结论与讨论通过本次实验，我们了解了概率统计的基本理论和方法，并通过投掷骰子的实验验证了骰子的随机性。

概率统计实验报告结论引言概率统计是数学中非常重要的一个分支，它利用统计方法对一定的随机现象进行描述、分析和预测。

本次实验中我们通过模拟实验的方式，利用概率统计的方法对一些实际问题进行了研究和分析。

实验一：骰子实验我们进行了一系列的骰子实验，通过投掷骰子并记录点数的方式来研究骰子的概率分布。

实验结果表明，投掷骰子时，每个面出现的概率是均等的，即每个面的概率是1/6。

这符合理论预期，也验证了概率统计中的等概率原理。

实验二：扑克牌实验通过抽取一副扑克牌中的若干张牌，并记录其点数和花色，我们研究了扑克牌中各个点数和花色的概率分布情况。

实验结果表明，52张扑克牌中各个点数和花色的概率分布近似均等，并且点数和花色之间是相互独立的。

这进一步验证了概率统计中的等概率原理和独立事件的性质。

实验三：掷硬币实验通过进行大量的抛硬币实验，我们研究了硬币正反面出现的概率分布情况。

实验结果表明，掷硬币时正面和反面出现的概率非常接近，都是1/2。

这也符合理论预期，并且进一步验证了概率统计中的等概率原理。

实验四：随机数生成器实验通过计算机程序生成随机数，并对其进行统计分析，我们研究了随机数生成器的质量问题。

实验结果表明，一个好的随机数生成器应该具备均匀分布、独立性和不可预测性等特征。

我们的实验结果显示，所使用的随机数生成器满足这些条件，从而可以被广泛应用于概率统计领域。

实验五：二项分布实验通过进行大量的二项分布实验，我们研究了二项分布的特性。

实验结果表明，二项分布在一定条件下可以近似成正态分布，这是概率统计中的重要定理之一。

实验结果还显示，二项分布的均值和方差与试验的次数和成功的概率有关，进一步验证了概率统计中与二项分布相关的理论。

总结通过本次概率统计实验，我们对骰子、扑克牌、硬币、随机数和二项分布等与概率统计相关的问题进行了研究和分析。

实验结果与理论预期基本一致，验证了概率统计中的一些重要原理和定理。

这些实验结果对我们的概率统计学习和应用有着重要的意义，同时也为我们在探索更深层次的概率统计问题提供了一定的启示和思路。

概率论与数理统计实验报告概率论与数理统计实验报告引言：概率论与数理统计是数学的两个重要分支，它们在现代科学研究和实际应用中起着重要的作用。

本次实验旨在通过实际操作，加深对概率论与数理统计的理解，并探索其在实际问题中的应用。

实验一：掷硬币实验实验目的：通过掷硬币实验，验证硬币正反面出现的概率是否为1/2。

实验步骤：1. 准备一枚硬币，标记正反面。

2. 进行100次连续掷硬币实验。

3. 记录每次实验中正面朝上的次数。

实验结果与分析：经过100次掷硬币实验，记录到正面朝上的次数为47次。

根据概率论的知识，理论上硬币正反面出现的概率应为1/2。

然而，实验结果显示正面朝上的次数并未达到理论值。

这表明在实际操作中，概率与理论可能存在一定的差异。

实验二：骰子实验实验目的：通过骰子实验，验证骰子的点数分布是否符合均匀分布。

实验步骤：1. 准备一个六面骰子。

2. 进行100次连续投掷骰子实验。

3. 记录每次实验中骰子的点数。

实验结果与分析：经过100次投掷骰子实验，记录到骰子点数的分布如下：1出现了17次；2出现了14次；3出现了20次；4出现了19次；5出现了16次；6出现了14次。

根据概率论的知识，理论上骰子的点数分布应符合均匀分布，即每个点数出现的概率相等。

然而，实验结果显示骰子点数的分布并未完全符合均匀分布。

这可能是由于实际操作的不确定性导致的结果差异。

实验三：正态分布实验实验目的：通过测量人体身高数据，验证人体身高是否符合正态分布。

实验步骤：1. 随机选择一定数量的被试者。

2. 测量每个被试者的身高。

3. 统计并绘制身高数据的频率分布直方图。

实验结果与分析：通过测量100名被试者的身高数据，统计得到的频率分布直方图呈现出典型的钟形曲线，符合正态分布的特征。

这与概率论中对正态分布的描述相吻合。

结论：通过以上实验，我们对概率论与数理统计的一些基本概念和方法有了更深入的了解。

实验结果也向我们展示了概率与理论之间的差异以及实际操作的不确定性。

数学实验报告概率班级：数学061学号：0602012010姓名: 杨丽概率A.实验指导书解读基本概念：1.随机现象：事前不可预言的现象，即在相同条件下重复进行试验，每次结果未必相同，或知道事物过去的状况，但未来的发展却不能完全肯定。

事物间的这种关系是属于偶然性的，这种现象叫做随机现象。

例如：以同样的方式抛置硬币却可能出现正面向上也可能出现反面向上；走到某十字路口时，可能正好是红灯，也可能正好是绿灯。

2.随机事件：在概率论中,将试验的结果称为事件。

每次试验中,可能发生也可能不发生,而在大量试验中具有某种规律性的事件称为随机事件。

3.随机事件的概率：概率是用来度量事件发生可能性大小的量.小概率事件很少发生,而大概率事件经常发生.随机事件A在n次实验中的频率是m/n，随着n的增大，该频率总在一个固定数P的附近摆动，随机事件A的概率即为这个固定数P。

4.随机变量及其分布：表示随机现象（在一定条件下，并不总是出现相同结果的现象称为随机现象）各种结果的变量（一切可能的样本点）。

离散型的随机变量的分布：0－1分布、二项分布、超几何分布、泊松（Poisson）分布；连续型随机变量的分布：均匀分布、正态分布N(μ，σ2)、指数分布。

由此，本次实验主要我们主要完成两件事:一．概率与频率的关系实验中，我们首先对随机事件A做理论上的研究，得出随机事件A的频率。

其次是要考虑合适的程序，利用计算机模拟随机事件发生的概率，模拟过程主要是通过改变n的值，得到不同的概率值，进而将这些不同的概率值与频率值比较，从而达到验证“频率稳定于概率”这一结论的目的。

二．探索研究随机变量的分布1.探寻随机变量不同的离散分布之间的联系并证明之；a.超几何分布和二项分布之间的联系；b.二项分布和Possion分布之间的联系。

实验需用不同的实例从数和形两个不同角度来探索超几何分布与二项分布的关系，二项分布与Possion分布的关系，继而用随机变量分布的定义加以证明探索结果。

一、实验目的1. 理解概率统计的基本概念和原理；2. 掌握运用概率统计方法解决实际问题的能力；3. 提高数据分析和处理能力。

二、实验内容1. 随机数生成实验2. 抽样实验3. 假设检验实验4. 估计与预测实验三、实验方法1. 随机数生成实验：使用计算机生成随机数，并分析其分布情况；2. 抽样实验：通过随机抽样，分析样本数据与总体数据的关系；3. 假设检验实验：根据样本数据，对总体参数进行假设检验；4. 估计与预测实验：根据历史数据，建立预测模型，对未来的数据进行预测。

四、实验步骤1. 随机数生成实验（1）设置随机数生成器的参数，如范围、种子等；（2）生成一定数量的随机数；（3）分析随机数的分布情况，如频率分布、直方图等。

2. 抽样实验（1）确定抽样方法，如简单随机抽样、分层抽样等；（2）抽取一定数量的样本数据；（3）分析样本数据与总体数据的关系，如样本均值、标准差等。

3. 假设检验实验（1）根据实际需求，设定原假设和备择假设；（2）计算检验统计量，如t统计量、卡方统计量等；（3）根据临界值表，判断是否拒绝原假设。

4. 估计与预测实验（1）收集历史数据，进行数据预处理；（2）选择合适的预测模型，如线性回归、时间序列分析等；（3）利用历史数据训练模型，并对未来数据进行预测。

五、实验结果与分析1. 随机数生成实验（1）随机数分布呈现均匀分布，符合概率统计的基本原理；（2）随机数的频率分布与理论分布相符。

2. 抽样实验（1）样本均值与总体均值接近，说明抽样效果较好；（2）样本标准差略大于总体标准差，可能受到抽样误差的影响。

3. 假设检验实验（1）根据检验统计量，拒绝原假设，说明总体参数存在显著差异；（2）根据临界值表，确定显著性水平，进一步分析差异的显著性。

4. 估计与预测实验（1）预测模型具有较高的准确率，说明模型能够较好地拟合历史数据；（2）对未来数据进行预测，结果符合实际情况。

六、实验结论1. 概率统计方法在解决实际问题中具有重要作用，能够提高数据分析和处理能力；2. 随机数生成实验、抽样实验、假设检验实验和估计与预测实验均取得了较好的效果；3. 通过本次实验，加深了对概率统计基本概念和原理的理解，提高了运用概率统计方法解决实际问题的能力。