2013高考最新样题三套卷数学理卷一

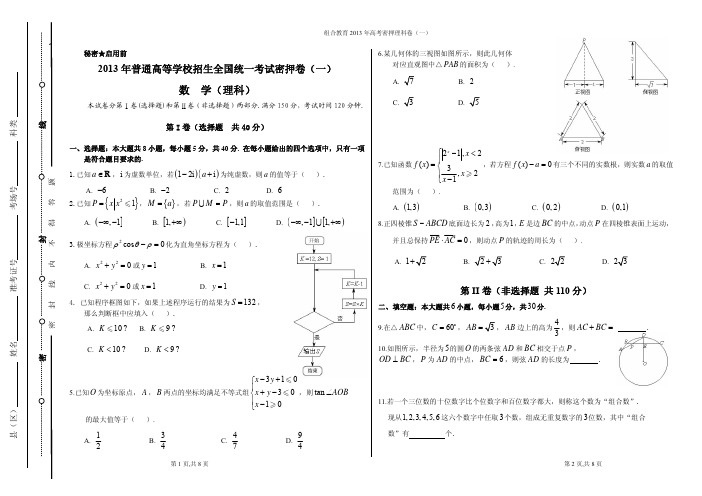
密县（区） 姓名 准考证号考场号 科类密 封 线 内 不 得 答 题秘密★启用前2013年普通高等学校招生全国统一考试密押卷（一）数 学（理科）本试卷分第Ⅰ卷(选择题)和第Ⅱ卷（非选择题）两部分.满分150分，考试时间120分钟.第I 卷（选择题 共40分）一、选择题：本大题共8小题，每小题5分，共40分. 在每小题给出的四个选项中，只有一项是符合题目要求的. 1.已知a ∈R ，i 为虚数单位，若()()12i i a −+为纯虚数，则a 的值等于（ ）.A. 6−B. 2−C. 2D. 62.已知{}21P x x =-，{}M a =，若P M P =U ，则a 的取值范围是（ ）.A. (],1−∞−B. [)1,+∞C. []1,1−D. (][),11,−∞−+∞U 3.极坐标方程2cos 0ρθρ−=化为直角坐标方程为（ ）.A. 220x y +=或1y = B. 1x =C. 220x y +=或1x = D. 1y =4. 已知程序框图如下，如果上述程序运行的结果为132S =，那么判断框中应填入（ ）.A. 10?K -B. 9?K -C. 10?K <D. 9?K <5.已知O 为坐标原点，A ，B 两点的坐标均满足不等式组3103010x y x y x −+⎧⎪+−⎨⎪−⎩--.，则tan AOB ∠的最大值等于（）.A. 12B. 34C. 47D.946.某几何体的三视图如图所示，则此几何体对应直观图中△PAB 的面积为（ ）.A. B. 2 C. D.7.已知函数21,2()3,21x x f x x x ⎧−<⎪=⎨⎪−⎩.，若方程()0f x a −=有三个不同的实数根，则实数a 的取值范围为（ ）.A. ()1,3B. ()0,3C.()0,2 D. ()0,18.正四棱锥S ABCD −底面边长为2，高为1，E 是边BC 的中点，动点P 在四棱锥表面上运动，并且总保持0PE AC ⋅=uuu r uuu r，则动点P 的轨迹的周长为（ ）.A. 1B. C. D.第II 卷（非选择题 共110分）二、填空题：本大题共6小题，每小题5分，共30分. 9.在△ABC 中，60C =o ，AB =AB 边上的高为43，则AC BC += ．10.如图所示，半径为5的圆O 的两条弦AD 和BC 相交于点P ，OD BC ⊥，P 为AD 的中点，6BC =，则弦AD 的长度为 ．11.若一个三位数的十位数字比个位数字和百位数字都大，则称这个数为“组合数”. 现从1,2,3,4,5,6这六个数字中任取3个数，组成无重复数字的3位数，其中“组合 数”有 个．12.在各项均为正数的数列{}n a中，对任意,m n∗∈Ν，都有m n m na a a+=⋅，若664a=，则9a= ．13.设若2lg,0()3d,0ax xf xx t t x>⎧⎪=⎨+⎪⎩∫-，()()11f f=，则a的值是 ．14. 若以曲线()y f x=上任意一点(,)M x y为切点作切线l，曲线上总存在异于点M的点(,)N x y′′，使得以点N为切点作切线l′满足l l′∥，则称曲线()y f x=具有“可平行性”.已知下列曲线：①3y x x=−；②1y xx=+；③siny x=；④2(2)lny x x=−+.其中具有“可平行性”的曲线是 ．（写出所有正确的编号）三．解答题：本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.15.（本小题满分13分）已知函数()()sinf x A xωϕ=+()0,0,πAωϕ>>< 的部分图象如图所示.（1）求函数()f x的解析式；（2）求函数()f x在区间ππ,64⎡⎤−⎢⎥⎣⎦上的最大值和最小值.16．（本小题满分14分）如图所示，四边形ABCD中，E是BC的中点，2,1,DB DC==AB AD=将左图沿直线BD折起，使得二面角A BD C−−为60,°（1）求证：AE⊥平面BDC；（2）求直线AC与平面ABD所成角的余弦值.密县（区） 姓名 准考证号考场号 科类密 封 线 内 不 得 答 题17.（本小题满分13分）甲、乙两人进行乒乓球比赛，约定每局胜者得1分，负者得0分，比赛进行到有一人比对方多2分或打满6局时停止. 设甲在每局中获胜的概率为P12P ⎛⎞>⎜⎟⎝⎠，且各局胜负相互独立. 已知第二局比赛结束时比赛停止的概率为59. （1）求P 的值；（2）设ξ表示比赛停止时比赛的局数，求随机变量ξ的分布列和数学期望E ξ.18.（本小题满分13分）已知函数()1()ln f x a x a x=+∈R . （1）求函数()f x 的单调区间和极值；（2）若对0a >，0x ∀>，都有()2ln 1ax x −-，求实数a 的取值范围.19.（本小题满分14分）已知椭圆1,C 抛物线2C 的焦点均在y 轴上，1C 的中心和2C 的顶点均为原点,O 从每条曲线上取两个点，将其坐标记录于下表中：（1）求12,C C 的标准方程；（2）设斜率不为0的动直线l 与1C 有且只有一个公共点,P 且与2C 的准线相交于点,Q 试探究：在坐标平面内是否存在定点,M 使得以PQ 为直径的圆恒过点?M 若存在，求出点M 的坐标；若不存在，请说明理由.20.（本小题满分13分）数列{}n a ，{}n b ()1,2,3,n =⋅⋅⋅由下列条件确定：①10a <，1b ②当2k .时，k a 与k b 满足：当110k k a b −−+.时，1k k a a −=，112k k k a b b −−+=；当 110k k a b −−+<时，112k k k a b a −−+=，1k k b b −=. （1）若11a =−，11b =，写出2a ，3a ，4a ，并求数列{}n a 的通项公式； （2）在数列{}n b 中，若12s b b b >>⋅⋅⋅>（3s .且s ∗∈Ν），试用1a ，1b 表示k b ，{}1,2,,k s ∈⋅⋅⋅；（3）在（1）的条件下，设数列{}()n c n ∗∈Ν满足112c =，0n c ≠，2212m n n mc c ma −+=−（其中m 为给定的不小于2的整数），求证：当n m -时，恒有1n c <.。

2013年高考课标一卷理科数学试题一、 选择题共12小题。

每小题5分，共60分。

1.已知集合{}{2|20,|A x x x B x x =->=<<，则 ( ) A.A∩B=∅ B.A ∪B=R C.B ⊆AD.A ⊆B2.若复数z 满足(34)|43|i z i -=+，则z 的虚部为()A .4-B .45-C .4D .453.为了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学.初中.高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是 ( )A .简单随机抽样B .按性别分层抽样C.按学段分层抽样D.系统抽样4.已知双曲线C ：22221x y a b -=（0,0a b >>C 的渐近线方程为A.14y x =±B.13y x =± C.12y x =± D.y x =±5.运行如下程序框图，如果输入的[1,3]t ∈-，则输出s 属于A.[3,4]- B .[5,2]- C.[4,3]- D.[2,5]-6.如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为 ( )A.35003cm π B .38663cm π C. 313723cm πD.320483cm π7.设等差数列{}n a 的前n 项和为11,2,0,3n m m m S S S S -+=-==，则m = ( )A .3B .4C.5D.68.某几何体的三视图如图所示，则该几何体的体积为A ．168π+B ．88π+C ．1616π+D ．816π+ 9.设m 为正整数，2()mx y +展开式的二项式系数的最大值为a ，21()m x y ++展开式的二项式系数的最大值为b ，若137a b =，则m = ( ) A .5B.6C.7D.810.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ，过点F 的直线交椭圆于,A B两点。

绝密★启封2013年普通高等学校招生全国统一考试文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至4页。

全卷满分150分。

考试时间120分钟。

注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷3至5页。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束，将本试题和答题卡一并交回。

第Ⅰ卷一、选择题共8小题。

每小题5分，共40分。

在每个小题给出的四个选项中，只有一项是符合题目要求的一项。

（1）已知集合A=｛1，2，3，4｝，B=｛x|x=n2，n∈A｝,则A∩B= ( ) （A）｛0｝（B）｛-1，,0｝（C）{0，1} （D）｛-1，,0，1}（2）错误！未找到引用源。

= ( )（A）-1 - 错误！未找到引用源。

i （B）-1 + 错误！未找到引用源。

i （C）1 + 错误！未找到引用源。

i （D）1 - 错误！未找到引用源。

i（3）从1，2，3，4中任取2个不同的数，则取出的2个数之差的绝对值为2的概率是（）（A）错误！未找到引用源。

（B）错误！未找到引用源。

（C）错误！未找到引用源。

（D）错误！未找到引用源。

（4）已知双曲线C：错误！未找到引用源。

= 1（a>0,b>0）的离心率为错误！未找到引用源。

，则C的渐近线方程为（）（A）y=±错误！未找到引用源。

x （B）y=±错误！未找到引用源。

x （C）y=±错误！未找到引用源。

x （D）y=±x（5）已知命题p：，则下列命题中为真命题的是：（）（A） p∧q （B）￢p∧q （C）p∧￢q （D）￢p∧￢q（6）设首项为1，公比为错误！未找到引用源。

的等比数列｛an ｝的前n项和为Sn，则（）（A）Sn =2an-1 （B）Sn=3an-2 （C）Sn=4-3an（D）Sn=3-2an（7）执行右面的程序框图，如果输入的t∈[-1，3]，则输出的s属于（A）[-3,4]（B）[-5,2]（C）[-4,3]（D）[-2,5]（8）O为坐标原点，F为抛物线C：y²=4x的焦点，P为C上一点，若丨PF丨=4，则△POF的面积为（A）2 （B）2（C）2（D）4（9）函数f（x）=（1-cosx）sinx在[-π，π]的图像大致为（10）已知锐角△ABC的内角A，B，C的对边分别为a，b，c，23cos²A+cos2A=0，a=7，c=6，则b= （A）10 （B）9 （C）8 （D）5（11）某几何函数的三视图如图所示，则该几何的体积为（A）18+8π（B）8+8π（C）16+16π（D）8+16π（12）已知函数f（x）= 若|f（x）|≥ax，则a的取值范围是（A）（-∞] （B）（-∞] (C)[-2,1] (D)[-2,0]第Ⅱ卷本卷包括必考题和选考题两个部分。

2013年全国新课标1卷高考理科数学试题，本试题适用于河南、河北、山西几个省份。

绝密★启封并使用完毕前2013年普通高等学校招生全国统一考试理科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至2页，第Ⅱ卷3至4页。

全卷满分150分。

考试时间120分钟。

注意事项：1. 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

第Ⅰ卷1至3页，第Ⅱ卷3至5页。

2. 答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置。

3. 全部答案在答题卡上完成，答在本试题上无效。

4. 考试结束，将本试题和答题卡一并交回。

第Ⅰ卷一、 选择题共12小题。

每小题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的一项。

1、已知集合A=｛x |x 2－2x ＞0｝，B=｛x |) A 、A ∩B= B 、A ∪B=R C 、B ⊆A 2、若复数z 满足 (3－4i)z ＝|4＋3i | ( ) A 、－4（B ）－45（C ）4 3地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽)、按性别分层抽样 C 、按学段分层抽样 D 、系统抽样4的离心率为52，则C 的渐近线方程为( )（C ）y =±12x（D ）y =±x51，3]，则输出的s 属于 ( )6、如图，有一个水平放置的透明无盖的正方体容器，容器高，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cmA 、500π3cm 3B 、866π3cm 3C 、1372π3cm 3D7，则m ＝ ( )89、设m 为正整数，(x ＋y )2m 展开式的二项式系数的最大值为a ，(x ＋y )2m ＋1展开式的二项式系数的最大值为b ，若13a =7b ，则m ＝ ( ) A 、5 B 、6 C 、7 D 、810、已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的右焦点为F的直线交椭圆于A 、B 两点。

绝密★启用前2013年普通高等学校招生全国统一考试(新课标I 卷)数学(理科)注意事项：1.本试卷分第Ⅰ卷（选择题）和第II 卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效。

4.考试结束后，将本试卷和答题卡一并交回。

第I 卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一个是符合题目要求的.（1）已知集合{}022>-=x x x A ，{}55B <<-=x x ，则（A ）AB =Φ （B ）A B =R （C ）A B ⊆ （D ）B A ⊆（2）若复数z 满足()i 34i 43+=-z（A ）4- （B ）54-（C ）4 （D ）54（3）为了解某地区中小学生的视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已经了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大.在下面的抽样方法中，最合理的抽样方法是（A ）简单的随机抽样 （B ）按性别分层抽样（C ）按学段分层抽样 （D ）系统抽样（4）已知双曲线C ：)0,0(12222>>=-b a by a x 的离心率为25，则C 的渐近线方程为（A ）x y 41±= （B ）x y 31±= （C ） x y 21±= （D ）x y ±= （5）执行右面的程序框图，如果输入的[]31t ，-∈，则输出的s 属于 （A ）[]43，- （B ）[]25，- （C ）[]34，- （D ）[]52，-（6）如图，有一个水平放置的透明无盖的正方体容器，容器高8 cm ，将一个球放在容器口，再向容器注水，当球面恰好接触水面时测得水深为6 cm ，如不计容器的厚度，则球的体积为 （A ）3cm 3500π （B ）3cm 3866π （C ）3cm 31372π （D ）3cm 32048π（7）设等差数列{}n a 的前n 项和为n S ，若21-=-m S ，0=m S ，31=+m S ，则=m（A ）3 （B ）4 （C ）5 （D ）6（8）某几何体的三视图如图所示，则该几何体的体积为 （A ）8π16+ （B ）8π8+ （C ）π6116+ （D ）16π8+设m 为正整数，()my x 2+展开式的二项式系数的最大值为a ，()12++m y x 展开式的二项式系数的最大值为b ，若b a 713=，则m ＝ （A ）5 （B ）6 （C ）7 （D ）8已知椭圆E ：)0(12222>>=+b a by a x 的右焦点为)03(,F ，过点F 的直线交椭圆E 于A 、B 两点。

2013年普通高等学校招生全国统一考试(课标全国卷Ⅰ)理数本卷满分150分,考试时间120分钟.第Ⅰ卷(选择题,共60分)一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合A={x|x2-2x>0},B={x|-√5<x<√5},则( )A.A∩B=⌀B.A∪B=RC.B⊆AD.A⊆B2.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )A.-4B.-45C.4 D.453.为了解某地区的中小学生的视力情况,拟从该地区的中小学生中抽取部分学生进行调查,事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异,而男女生视力情况差异不大.在下面的抽样方法中,最合理的抽样方法是( )A.简单随机抽样B.按性别分层抽样C.按学段分层抽样D.系统抽样4.已知双曲线C:x 2a2-y2b2=1(a>0,b>0)的离心率为√52,则C的渐近线方程为( )A.y=±1xB.y=±1xC.y=±1xD.y=±x5.执行下面的程序框图,如果输入的t∈[-1,3],则输出的s属于( )A.[-3,4]B.[-5,2]C.[-4,3]D.[-2,5]6.如图,有一个水平放置的透明无盖的正方体容器,容器高8 cm,将一个球放在容器口,再向容器内注水,当球面恰好接触水面时测得水深为6 cm,如果不计容器的厚度,则球的体积为( )A.500π3cm 3B.866π3cm 3C.1 372π3cm 3D.2 048π3cm 37.设等差数列{a n }的前n 项和为S n ,若S m-1=-2,S m =0,S m+1=3,则m=( ) A.3B.4C.5D.68.某几何体的三视图如图所示,则该几何体的体积为( )A.16+8πB.8+8πC.16+16πD.8+16π9.设m 为正整数,(x+y)2m展开式的二项式系数的最大值为a,(x+y)2m+1展开式的二项式系数的最大值为b.若13a=7b,则m=( ) A.5B.6C.7D.810.已知椭圆E:x 22+y 2b2=1(a>b>0)的右焦点为F(3,0),过点F 的直线交E 于A,B 两点.若AB 的中点坐标为(1,-1),则E 的方程为( )A.x 245+y 236=1B.x 236+y 227=1C.x 227+y 218=1D.x 218+y 29=1 11.已知函数f(x)={-x 2+2x ,x ≤0,ln (x +1),x >0.若|f(x)|≥ax,则a 的取值范围是( )A.(-∞,0]B.(-∞,1]C.[-2,1]D.[-2,0]12.设△A n B n C n 的三边长分别为a n ,b n ,c n ,△A n B n C n 的面积为S n ,n=1,2,3,….若b 1>c 1,b 1+c 1=2a 1,a n+1=a n ,b n+1=c n +a n 2,c n+1=b n +a n2,则( )A.{S n }为递减数列B.{S n }为递增数列C.{S 2n-1}为递增数列,{S 2n }为递减数列D.{S 2n-1}为递减数列,{S 2n }为递增数列第Ⅱ卷(非选择题,共90分)本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须作答.第22题~第24题为选考题,考生根据要求作答. 二、填空题:本大题共4小题,每小题5分.13.已知两个单位向量a,b 的夹角为60°,c=ta+(1-t)b.若b·c=0,则t= . 14.若数列{a n }的前n 项和S n =23a n +13,则{a n }的通项公式是a n = . 15.设当x=θ时,函数f(x)=sin x-2cos x 取得最大值,则cos θ= .16.若函数f(x)=(1-x 2)(x 2+ax+b)的图象关于直线x=-2对称,则f(x)的最大值为 . 三、解答题:解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)如图,在△ABC 中,∠ABC=90°,AB=√3,BC=1,P 为△ABC 内一点,∠BPC=90°. (Ⅰ)若PB=12,求PA;(Ⅱ)若∠APB=150°,求tan∠PBA.18.(本小题满分12分)如图,三棱柱ABC-A 1B 1C 1中,CA=CB,AB=AA 1,∠BAA 1=60°. (Ⅰ)证明:AB⊥A 1C;(Ⅱ)若平面ABC⊥平面AA 1B 1B,AB=CB,求直线A 1C 与平面BB 1C 1C 所成角的正弦值.19.(本小题满分12分)一批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验.,且各件产品假设这批产品的优质品率为50%,即取出的每件产品是优质品的概率都为12是否为优质品相互独立.(Ⅰ)求这批产品通过检验的概率;(Ⅱ)已知每件产品的检验费用为100元,且抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望.20.(本小题满分12分)已知圆M:(x+1)2+y2=1,圆N:(x-1)2+y2=9,动圆P与圆M外切并且与圆N内切,圆心P的轨迹为曲线C.(Ⅰ)求C的方程;(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.21.(本小题满分12分)设函数f(x)=x2+ax+b,g(x)=e x(cx+d).若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P 处有相同的切线y=4x+2.(Ⅰ)求a,b,c,d的值;(Ⅱ)若x≥-2时, f(x)≤kg(x),求k的取值范围.请考生从第22、23、24三题中任选一题作答,多选、多答,按所选的首题进行评分;不选,按本选考题的首题进行评分.22.(本小题满分10分)选修4—1:几何证明选讲如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.(Ⅰ)证明:DB=DC;(Ⅱ)设圆的半径为1,BC=√3,延长CE交AB于点F,求△BCF外接圆的半径.23.(本小题满分10分)选修4—4:坐标系与参数方程已知曲线C 1的参数方程为{x =4+5cost ,y =5+5sint (t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ. (Ⅰ)把C 1的参数方程化为极坐标方程;(Ⅱ)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).24.(本小题满分10分)选修4—5:不等式选讲 已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3. (Ⅰ)当a=-2时,求不等式f(x)<g(x)的解集;(Ⅱ)设a>-1,且当x∈[-a,1)时, f(x)≤g(x),求a 的取值范围.2013年普通高等学校招生全国统一考试(课标全国卷Ⅰ)一、选择题1.B 化简A={x|x>2或x<0},而B={x|-√5<x<√5},所以A ∩B={x|-√5<x<0或2<x<√5},B 项错误;A ∪B=R ,B 项正确;A 与B 没有包含关系,C 项与D 项均错误.故选B.2.D ∵|4+3i|=√42+32=5,∴z=53-4i =5(3+4i)25=35+45i,虚部为45,故选D.3.C 因为男女视力情况差异不大,而学段的视力情况有较大差异,所以应按学段分层抽样,故选C.评析 本题考查了分层抽样,准确理解分层抽样的意义是解题关键. 4.C ∵ba =√e 2-1=√54-1=12,∴C 的渐近线方程为y=±12x.故选C.5.A 由框图知s 是关于t 的分段函数:s={3t,-1≤t <1,4t -t 2,1≤t ≤3,当t ∈[-1,1)时,s ∈[-3,3);当t ∈[1,3]时,s=4t-t 2=4-(t-2)2∈[3,4],故s ∈[-3,4],故选A.6.A 设球心为O,正方体上底面中心为A,上底面一边的中点为B,在Rt △OAB 中,|OA|=R-2(cm),|AB|=4(cm),|OB|=R(cm),由R 2=(R-2)2+42得R=5(cm),∴V 球=43πR 3=5003π(cm 3).故选A.评析 本题考查了正方体和球的组合体,考查了空间想象能力.利用勾股定理求出球半径R 是解题的关键.7.C 解法一:∵S m-1=-2,S m =0,S m+1=3,∴a m =S m -S m-1=2,a m+1=S m+1-S m =3,∴公差d=a m+1-a m =1,由S n =na 1+n(n -1)2d=na 1+n(n -1)2,得{ma 1+m(m -1)2=0, ①(m -1)a 1+(m -1)(m -2)2=-2.② 由①得a 1=1-m 2,代入②可得m=5.解法二:∵数列{a n }为等差数列,且前n 项和为S n ,∴数列{Sn n } 也为等差数列. ∴S m -1m -1+Sm+1m+1=2S m m,即-2m -1+3m+1=0,即m=5.故选C.评析 本题考查等差数列前n 项和的基本运算,若能掌握等差数列的性质,解决此题可简化运算.8.A 由三视图可知该几何体由长方体和圆柱的一半组成.其中长方体的长、宽、高分别为4、2、2,圆柱的底面半径为2,高为4.所以该几何体的体积为V=4×2×2+12π×22×4=16+8π.故选A.9.B 由题意得:a=C 2m m ,b=C 2m+1m ,所以13C 2m m =7C 2m+1m ,∴13·(2m)!m!·m!=7·(2m+1)!m!·(m+1)!,∴7(2m+1)m+1=13,解得m=6,选B.10.D 直线AB 的斜率k=0+13-1=12,设A(x 1,y 1),B(x 2,y 2),则{x 12a 2+y 12b 2=1, ①x 22a 2+y 22b2=1,② ①-②得y 1-y2x 1-x 2=-b 2a 2·x 1+x 2y 1+y 2.即k=-b 2a 2×2-2,∴b 2a2=12. ③又a 2-b 2=c 2=9, ④由③④得a 2=18,b 2=9.所以椭圆方程为x 218+y 29=1,故选D.评析 本题考查了直线和椭圆的位置关系,考查了线段的中点问题.本题也可利用韦达定理解决中点问题.11.D 由题意作出y=|f(x)|的图象:由题意结合图象知,当a>0时,y=ax 与y=ln(x+1)在x>0时必有交点,所以a ≤0.当x ≥0时,|f(x)|≥ax 显然成立;当x<0时,|f(x)|=x 2-2x ≥ax,则a ≥x-2恒成立,又x-2<-2,∴a≥-2.综上,-2≤a ≤0,故选D.评析 本题考查了函数的综合应用,考查了数形结合的能力;借助基本初等函数的图象缩小参数范围是解题关键. 12.B 由b n+1=a n +c n2,c n+1=b n +a n2得b n+1+c n+1=a n +12(b n +c n ),①b n+1-c n+1=-12(b n -c n ),②由a n+1=a n 得a n =a 1,代入①得b n+1+c n+1=a 1+12(b n +c n ),∴b n+1+c n+1-2a 1=12(b n +c n -2a 1),∵b 1+c 1-2a 1=2a 1-2a 1=0,∴b n +c n =2a 1>|B n C n |=a 1,所以点A n 在以B n 、C n 为焦点且长轴长为2a 1的椭圆上(如图).由b 1>c 1得b 1-c 1>0,所以|b n+1-c n+1|=12(b n -c n ), 即|b n -c n |=(b 1-c 1)·(12)n -1,所以当n 增大时|b n -c n |变小,即点A n 向点A 处移动,即边B n C n 上的高增大,又|B n C n |=a n =a 1不变,所以{S n }为递增数列.二、填空题 13.答案 2解析 解法一:∵b ·c =0, ∴b [t a +(1-t)b ]=0, t a ·b +(1-t)·b 2=0, 又∵|a |=|b |=1,<a,b >=60°, ∴12t+1-t=0,t=2.解法二:由t+(1-t)=1知向量a 、b 、c 的终点A 、B 、C 共线,在平面直角坐标系中设a =(1,0),b =(12,√32),则c =(32,-√32). 把a 、b 、c 的坐标代入c =t a +(1-t)b ,得t=2.评析 本题考查了向量的运算,利用三点共线的条件得到c 的坐标是解题关键. 14.答案 (-2)n-1解析 由S n =23a n +13得:当n ≥2时,S n-1=23a n-1+13,∴当n ≥2时,a n =-2a n-1,又n=1时,S 1=a 1=23a 1+13,a 1=1,∴a n =(-2)n-1. 15.答案 -2√55解析 由辅助角公式得:f(x)=√5(√55sinx -2√55cosx)=√5sin(x-φ),其中sin φ=2√55,cos φ=√55,由x=θ,f(x)取得最大值得:sin(θ-φ)=1,∴θ-φ=2kπ+π2,k ∈Z ,即θ=φ+π2+2kπ,∴cos θ=cos (φ+π2)=-sinφ=-2√55. 评析 本题考查了辅助角公式的应用,准确掌握辅助角的含义是解题关键. 16.答案 16解析 由f(x)=(1-x 2)(x 2+ax+b)的图象关于直线x=-2对称,则有{f(0)=f(-4),f(1)=f(-5),即{b =-15(16-4a +b),0=-24(25-5a +b), 解得a=8,b=15,∴f(x)=(1-x 2)(x 2+8x+15)=(1-x 2)[(x+4)2-1],令x+2=t,则x=t-2,t ∈R . ∴y=f(t)=[1-(t-2)2][(t-2)2+8(t-2)+15] =(4t-t 2-3)(4t+t 2+3)=16t 2-(t 2+3)2=16t 2-t 4-6t 2-9=16-(t 2-5)2,∴当t 2=5时y max =16.三、解答题17.解析 (Ⅰ)由已知得,∠PBC=60°,所以∠PBA=30°.在△PBA 中,由余弦定理得PA 2=3+14-2×√3×12cos 30°=74.故PA=√72.(Ⅱ)设∠PBA=α,由已知得PB=sin α.在△PBA 中,由正弦定理得√3sin150°=sinαsin(30°-α), 化简得√3cos α=4sin α.所以tan α=√34,即tan ∠PBA=√34.评析 本题考查了利用正弦定理和余弦定理解三角形,考查了运算求解能力和分析、解决问题的能力.题目新颖且有一定的难度,通过PB 把△PBC 和△PAB 联系起来利用正弦定理是解题关键.18.解析 (Ⅰ)取AB 的中点O,连结OC,OA 1,A 1B.因为CA=CB,所以OC ⊥AB.由于AB=AA 1,∠BAA 1=60°,故△AA 1B 为等边三角形,所以OA 1⊥AB.因为OC ∩OA 1=O,所以AB ⊥平面OA 1C.又A 1C ⊂平面OA 1C,故AB ⊥A 1C.(Ⅱ)由(Ⅰ)知OC ⊥AB,OA 1⊥AB.又平面ABC ⊥平面AA 1B 1B,交线为AB,所以OC ⊥平面AA 1B 1B,故OA,OA 1,OC 两两相互垂直.以O 为坐标原点,OA ⃗⃗⃗⃗⃗ 的方向为x 轴的正方向,|OA ⃗⃗⃗⃗⃗ |为单位长,建立如图所示的空间直角坐标系O-xyz.由题设知A(1,0,0),A 1(0,√3,0),C(0,0,√3),B(-1,0,0).则BC ⃗⃗⃗⃗⃗ =(1,0,√3),BB ⃗⃗⃗⃗⃗ 1=AA ⃗⃗⃗⃗⃗ 1=(-1,√3,0),A 1C ⃗⃗⃗⃗⃗⃗⃗ =(0,-√3,√3).设n =(x,y,z)是平面BB 1C 1C 的法向量,则{n ·BC ⃗⃗⃗⃗⃗ =0,n ·BB⃗⃗⃗⃗⃗ 1=0.即{x +√3z =0,-x +√3y =0.可取n =(√3,1,-1). 故cos<n ,A 1C ⃗⃗⃗⃗⃗⃗⃗ >=n ·A 1C ⃗⃗⃗⃗⃗⃗⃗⃗ |n||A 1C ⃗⃗⃗⃗⃗⃗⃗⃗ |=-√105. 所以A 1C 与平面BB 1C 1C 所成角的正弦值为√105. 19.解析 (Ⅰ)设第一次取出的4件产品中恰有3件优质品为事件A 1,第一次取出的4件产品全是优质品为事件A 2,第二次取出的4件产品都是优质品为事件B 1,第二次取出的1件产品是优质品为事件B 2,这批产品通过检验为事件A,依题意有A=(A 1B 1)∪(A 2B 2),且A 1B 1与A 2B 2互斥,所以P(A)=P(A 1B 1)+P(A 2B 2)=P(A 1)P(B 1|A 1)+P(A 2)P(B 2|A 2)=416×116+116×12=364.(Ⅱ)X 可能的取值为400,500,800,并且P(X=400)=1-416-116=1116,P(X=500)=116,P(X=800)=14.所以X 的分布列为X400 500 800 P1116 116 14EX=400×1116+500×116+800×14=506.25.20.解析 由已知得圆M 的圆心为M(-1,0),半径r 1=1;圆N 的圆心为N(1,0),半径r 2=3.设圆P 的圆心为P(x,y),半径为R.(Ⅰ)因为圆P 与圆M 外切并且与圆N 内切,所以|PM|+|PN|=(R+r 1)+(r 2-R)=r 1+r 2=4.由椭圆的定义可知,曲线C 是以M 、N 为左、右焦点,长半轴长为2,短半轴长为√3的椭圆(左顶点除外),其方程为x 24+y 23=1(x ≠-2).(Ⅱ)对于曲线C 上任意一点P(x,y),由于|PM|-|PN|=2R-2≤2,所以R ≤2,当且仅当圆P 的圆心为(2,0)时,R=2.所以当圆P 的半径最长时,其方程为(x-2)2+y 2=4.若l 的倾斜角为90°,则l 与y 轴重合,可得|AB|=2√3.若l 的倾斜角不为90°,由r 1≠R 知l 不平行于x 轴,设l 与x 轴的交点为Q,则|QP||QM|=R r 1,可求得Q(-4,0),所以可设l:y=k(x+4).由l 与圆M 相切得√1+k 2=1,解得k=±√24. 当k=√24时,将y=√24x+√2代入x 24+y 23=1,并整理得7x 2+8x-8=0,解得x 1,2=-4±6√27.所以|AB|=√1+k 2|x 2-x 1|=187. 当k=-√24时,由图形的对称性可知|AB|=187.综上,|AB|=2√3或|AB|=187. 评析 本题考查了直线和圆的位置关系,考查了椭圆的定义和方程,考查了分类讨论的方法和运算求解能力.利用数形结合的方法是解题的关键.在求曲线C 的方程时容易忽视对左顶点和直线倾斜角为90°时的讨论而造成失分.21.解析 (Ⅰ)由已知得f(0)=2,g(0)=2, f '(0)=4,g'(0)=4.而f '(x)=2x+a,g'(x)=e x (cx+d+c),故b=2,d=2,a=4,d+c=4.从而a=4,b=2,c=2,d=2.(Ⅱ)由(Ⅰ)知, f(x)=x 2+4x+2,g(x)=2e x (x+1).设函数F(x)=kg(x)-f(x)=2ke x (x+1)-x 2-4x-2,则 F'(x)=2ke x (x+2)-2x-4=2(x+2)(ke x -1).由题设可得F(0)≥0,即k≥1.令F'(x)=0,得x1=-ln k,x2=-2.(i)若1≤k<e2,则-2<x1≤0.从而当x∈(-2,x1)时,F'(x)<0;当x∈(x1,+∞)时,F'(x)>0.即F(x)在(-2,x1)上单调递减,在(x1,+∞)上单调递增.故F(x)在[-2,+∞)上的最小值为F(x1).而F(x1)=2x1+2-x12-4x1-2=-x1(x1+2)≥0.故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.(ii)若k=e2,则F'(x)=2e2(x+2)(e x-e-2).从而当x>-2时,F'(x)>0,即F(x)在(-2,+∞)上单调递增.而F(-2)=0,故当x≥-2时,F(x)≥0,即f(x)≤kg(x)恒成立.(iii)若k>e2,则F(-2)=-2ke-2+2=-2e-2(k-e2)<0.从而当x≥-2时, f(x)≤kg(x)不可能恒成立.综上,k的取值范围是[1,e2].评析本题考查了导数的几何意义以及利用导数研究函数的单调性,考查了分类与整合、函数与方程的思想;结合特值限定参数的范围,可减少分类的情况,有利于提高效率,掌握利用两根大小作为讨论的分界点,是解题关键.22.解析(Ⅰ)连结DE,交BC于点G.由弦切角定理得,∠ABE=∠BCE.而∠ABE=∠CBE,故∠CBE=∠BCE,BE=CE.又因为DB⊥BE,所以DE为直径,∠DCE=90°,由勾股定理可得DB=DC.(Ⅱ)由(Ⅰ)知,∠CDE=∠BDE,DB=DC,.故DG是BC的中垂线,所以BG=√32设DE 的中点为O,连结BO,则∠BOG=60°.从而∠ABE=∠BCE=∠CBE=30°,所以CF ⊥BF,故Rt △BCF 外接圆的半径等于√32.23.解析 (Ⅰ)将{x =4+5cost,y =5+5sint消去参数t,化为普通方程(x-4)2+(y-5)2=25, 即C 1:x 2+y 2-8x-10y+16=0.将{x =ρcosθ,y =ρsinθ代入x 2+y 2-8x-10y+16=0得 ρ2-8ρcos θ-10ρsin θ+16=0.所以C 1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0.(Ⅱ)C 2的普通方程为x 2+y 2-2y=0.由{x 2+y 2-8x -10y +16=0,x 2+y 2-2y =0,解得{x =1,y =1或{x =0,y =2. 所以C 1与C 2交点的极坐标分别为(√2,π4),(2,π2).24.解析 (Ⅰ)当a=-2时,不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.设函数y=|2x-1|+|2x-2|-x-3,则y={ -5x, x <12,-x -2,12≤x ≤1,3x -6,x >1.其图象如图所示.从图象可知,当且仅当x ∈(0,2)时,y<0.所以原不等式的解集是{x|0<x<2}.(Ⅱ)当x ∈[-a 2,12)时, f(x)=1+a. 不等式f(x)≤g(x)化为1+a ≤x+3.所以x ≥a-2对x ∈[-a 2,12)都成立.故-a 2≥a-2,即a ≤43.]. 从而a的取值范围是(-1,43。

2013年全国高考新课标理科数学第一卷一、选择题共12小题。

每小题5分，共60分。

在每个小题给出的四个选项中，只有一项是符合题目要求的一项。

1、已知集合A=｛x|x2－2x＞0｝，B=｛x|－5＜x＜5｝，则( )A、A∩B=∅B、A B=RC、B⊆AD、A⊆B2、若复数z满足错误！未找到引用源。

(3－4i)z＝|4＋3i |，则z的虚部为()A、－4 （B）－45错误！未找到引用源。

（C）4 （D）453、为了解某地区的中小学生视力情况，拟从该地区的中小学生中抽取部分学生进行调查，事先已了解到该地区小学、初中、高中三个学段学生的视力情况有较大差异，而男女生视力情况差异不大，在下面的抽样方法中，最合理的抽样方法是( )A、简单随机抽样B、按性别分层抽样错误！未找到引用源。

C、按学段分层抽样D、系统抽样【答案】C；【解析】不同的学段在视力状况上有所差异，所以应该按照年段分层抽样. 【考点定位】本题考查随机抽样，考查学生对概念的理解.4、已知双曲线C:x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率为错误！未找到引用源。

，则C的渐近线方程为()A 、y =±错误！未找到引用源。

x （B ）y =±错误！未找到引用源。

x（C ）y =±错误！未找到引用源。

x（D ）y =±x5、执行右面的程序框图，如果输入的t ∈[－1，3]，则输出的s 属于()A 、[－3,4]B 、[－5,2]C 、[－4,3]D 、[－2,5]【答案】A ；【解析】若[)1,1t ∈-，则[)33,3S t =∈-；若[]1,3t ∈，[]243,4S t t =-∈；综上所述[]3,4S ∈-.【考点定位】本题考查算法框图，考查学生的逻辑推理能力.6、如图，有一个水平放置的透明无盖的正方体容器，容器高8cm ，将一个球放在容器口，再向容器内注水，当球面恰好接触水面时测得水深为6cm ，如果不计容器的厚度，则球的体积为( )A、500π3cm3B、866π3cm3错误！未找到引用源。

2013年高考数学全国卷1(完整试题+答案+解析)DD ．159.函数x x x f 1lg )(-=的零点所在的区间是(B) A ．(]1,0 B ．(]10,1 C ．(]100,10D ．),100(+∞10.过直线y x =上一点P 引圆22670x y x +-+=的切线，则切线长的最小值为(C)A ．22B ． 223C ．210D ．211.已知函数bax x x f 2)(2-+=.若b a ,都是区间[]4,0内的数，则使0)1(>f 成立的概率是 (C)A ．43B ．41 C ．83D ．8512.已知双曲线的标准方程为116922=-y x ，F 为其右焦点，21,A A 是实轴的两端点，设P 为双曲线上不同于21,A A 的任意一点，直线P A P A 21,与直线a x =分别交于两点N M ,,若0=⋅FM ,则a 的值为(B)A ．916 B ．59 C ．925D ．516 双曲线 x^2/9-y^2/16=1,右焦点F(5.0)，A1(-3,0)，A2(3,0) 设P(x,y) M (a,m),N(a,n) ∵P,A1,M 三点共线， ∴m/(a+3)=y/(x+3) ∴m=y(a+3)/(x+3)∵P,A2,N 三点共线， ∴n/(a-3)=y/(x-3) ∴n=y(a-3)/(x-3) ∵x^2/9-y^2/16=1 ∴(x^2-9)/9=y^2/16 ∴y^2/(x^2-9)=16/9FM 向量=(a-5,y(a+3)/(x+3)) FN 向量=(a-5,y(a-3)/(x-3)) FM 向量*FN 向量=(a-5)^2+y^2(a^2-9)/(x^2-9) =(a-5)^2+16(a^2-9)/9 ∵FM 向量*FN 向量=0 ∴(a-5)^2+16(a^2-9)/9=0 25a^2-90a+81=0 ∴a=9/5第Ⅱ卷（非选择题 共90分）注意事项：1． 请用0.5毫米的黑色签字笔将每题的答案填写在第Ⅱ卷答题纸的指定位置．书写的答案如需改动，要先划掉原来的答案，然后再写上新答案．题图第132． 不在指定答题位置答题或超出答题区域书写的答案无效．在试题卷上答题无效． 3． 第Ⅱ卷共包括填空题和解答题两道大题． 二、填空题：本大题共44分，共16分．13.如图所示的程序框图输结果为____2______.14. 若一个底面是正三角形的棱柱的正视图如下图所示，其顶点都在一个球面上，则该球的表面积为_π319_________.如图。