纳米压痕实验PPT课件

图解浸胶(二十四)
纳米压痕技术对RFL/橡胶粘合界面的分析
纳米压痕技术实验是可以针对RFL/橡胶层的粘合界面进行的。

样品准备与SED-EDX电镜扫描样品一样。

纳米压痕试验采用一种商用的原子力显微镜进行的（Dimension3100配有纳米级精度Veeco的IIIa控制器）。

在实验中采用了三角形硅氮悬臂以及硅氮tips(DI) vacuum，预估的弹性系数为0.6nN/nm，预估的TIP半径为50微米。

RFL/橡胶界面的模量轮廓是通过对界面处的进行线扫描而获得的。

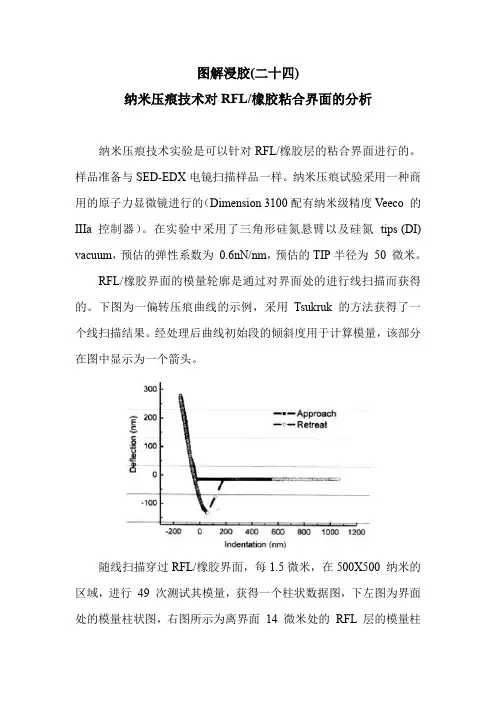
下图为一偏转压痕曲线的示例，采用Tsukruk的方法获得了一个线扫描结果。

经处理后曲线初始段的倾斜度用于计算模量，该部分在图中显示为一个箭头。

随线扫描穿过RFL/橡胶界面，每1.5微米，在500X500纳米的区域，进行49次测试其模量，获得一个柱状数据图，下左图为界面处的模量柱状图，右图所示为离界面14微米处的RFL层的模量柱
状图。

可以看出界面处的模量柱状图的分布区域比较宽。

下图为对RFL/橡胶界面的全纳米压痕线扫描结果。

当靠近RFL/橡胶界面时，RFL的模量提高，分布也变宽；在橡胶侧，在离界面的10微米处，模量也有一定的提高。

这可能是橡胶并不是一种均质聚合物质，含有大量的刚硬添加剂，比如炭黑。

忽略这些数据，橡胶的模量大致稳定。

该图与SED-EDX对硫，锌，钠的含量线扫描结果是相吻合的,如下图：
以上说明对于RFL/橡胶的粘合，橡胶中硫化剂向RFL中的迁移情况对其是影响较大的因素。

纳米压痕实验一、实验目的1. 了解材料微纳米力学测试系统的构造、工作原理。

2. 掌握载荷-位移曲线的分析手段。

3. 用纳米压痕方法测定电沉积镍镀层的杨氏模量与硬度。

二、实验仪器和设备TriboIndenter 型材料微纳米力学测试系统(见附录)三、实验原理与方法纳米压痕技术又称深度敏感压痕技术，它通过计算机控制载荷连续变化，并在线监测压入深度。

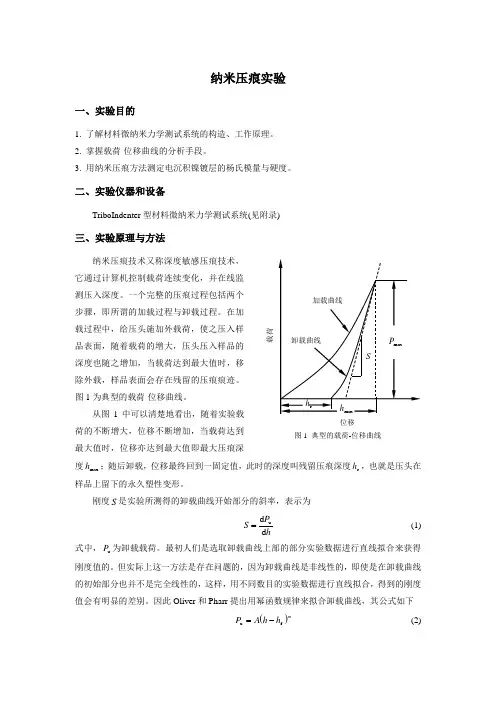
一个完整的压痕过程包括两个步骤，即所谓的加载过程与卸载过程。

在加载过程中，给压头施加外载荷，使之压入样品表面，随着载荷的增大，压头压入样品的深度也随之增加，当载荷达到最大值时，移除外载，样品表面会存在残留的压痕痕迹。

图1为典型的载荷-位移曲线。

从图1中可以清楚地看出，随着实验载荷的不断增大，位移不断增加，当载荷达到最大值时，位移亦达到最大值即最大压痕深度max h ；随后卸载，位移最终回到一固定值，此时的深度叫残留压痕深度r h ，也就是压头在样品上留下的永久塑性变形。

刚度S 是实验所测得的卸载曲线开始部分的斜率，表示为hP S d d u=(1) 式中，u P 为卸载载荷。

最初人们是选取卸载曲线上部的部分实验数据进行直线拟合来获得刚度值的。

但实际上这一方法是存在问题的，因为卸载曲线是非线性的，即使是在卸载曲线的初始部分也并不是完全线性的，这样，用不同数目的实验数据进行直线拟合，得到的刚度值会有明显的差别。

因此Oliver 和Pharr 提出用幂函数规律来拟合卸载曲线，其公式如下()mh h A P f u -= (2)载荷位移图1 典型的载荷-位移曲线其中，A 为拟合参数，f h 为残留深度，即为r h ，指数m 为压头形状参数。

m ，A 和f h 均由最小二乘法确定。

对式(2)进行微分就可得到刚度值，即()1f max u maxd d -=-==m h h h h A m hP S (3)该方法所得的刚度值与所取的卸载数据多少无关，而且十分接近利用很少卸载数据进行线性拟合的结果，因此用幂函数规律拟合卸载曲线是实际可行的好方法。

纳米压痕技术（英：Nanoindentation），也称深度敏感压痕技术（英：Depth-Sensing Indentation, DSI)，是最简单的测试材料力学性质的方法之一，可以在纳米尺度上测量材料的各种力学性质，如载荷-位移曲线、弹性模量(Elastic Modulus)、硬度(Hardness)、断裂韧性(Frac ture Toughness)、应变硬化效应(Strain Hardening Effect)、粘弹性使材料发生一定弹性变形的应力也越大，即材料刚度越大，亦即在一定应力作用下，发生弹性变形越小。

弹性模量E是指材料在外力作用下产生单位弹性变形所需要的应力。

它是反映材料抵抗弹性变形能力的指标，相当于普通弹簧中的刚度。

晶体管，本名是半导体三极管，是内部含有两个PN结，外部通常为三个引出电极的半导体器件。

它对电信号有放大和开关等作用，应用十分广泛。

能隙（Bandgap energy gap）或译作能带隙，在固态物理学中泛指半导体或是绝缘体的价带（valenc e band）(价带[1]（valenc e band）或称价电带，通常是指半导体或绝缘体中，在绝对零度下能被电子占满的最高能带。

对半导体而言，此能带中的能级基本上是连续的。

全充满的能带中的电子不能在固体中自由运动。

但若该电子受它可吸收足够能量而跳入下一个容许的最高能区，从而使价带变成部分充带中留下的电子可在固体中自由运动。

)顶端至传导带(传导带（conduction band）系指半导体或是绝缘体材料中，一个电子所具有能量的范围。

这个能量的范围高于价带（valence band），而所有在传导带中的电子均可经由外在的电场加速而形成电流)（conduction band）底端的能量差距, 对一个本征半导体（intrinsic semic onduc tor）而言，其导电性与能隙的大小有关，只有获得足够能量的电子才能从价带被激发，跨过能隙并跃迁至传导带。