知识点三
画二次函数的图象,列表时取的点越多,图象往往越准确,但是 一般采用“五点法”或“七点法”画图,画图时应注意: (1)描点法所画的图象只是整个函数图象的一部分,是近似的, 由于x可取一切实数,所以图象是向两方无限延伸的; (2)点取得越多,图象画得越精确,在限定条件下(即限定自变量 的取值范围)或在实际问题中,函数的图象必须要根据自变量 的取值范围取其中的一部分; (3)所画图象必须平滑(符合点的发展变化的趋势),尤其是顶点 不能画成“尖”形的.
22.1.2
二次函数y=ax2的图象和性质
知识点一
知识点二
知识点三
知识点一二次函数y=x2的图象和性质 二次函数y=ax2+bx+c的图象是抛物线,对称轴与抛物线的交点叫 做顶点,顶点是抛物线的最低点或最高点. 对于特殊的二次函数y=x2,对称轴是y轴,顶点是(0,0),顶点是它的 最低点,在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛 物线从左到右上升.也就是说,当x<0时,y随x的增大而减小;当x>0 时,y随x的增大而增大. 名师解读:理解和记忆二次函数的性质时,可以从y=x2得到启发, 其他二次函数的图象及性质可类比y=x2的图象和性质,主要从开口 方向、对称轴、顶点、增减性等几个方面去进行.
知识点一
知识点二
知识点三
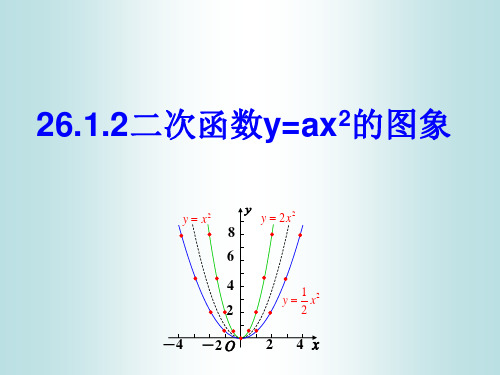
知识点二y=ax2的图象 一般地,抛物线y=ax2的对称轴是y轴,顶点是原点.当a>0时,抛物线 的开口向上,顶点是抛物线的最低点;当a<0时,抛物线的开口向下, 顶点是抛物线的最高点.对于y=ax2,|a|越大,抛物线的开口越小. 名师解读:二次函数y=ax2的图象是抛物线,结合图象可知,二次项 系数a的符号决定了开口方向,|a|决定了开口的大小.