单自由度机系统动力学——牛头刨床运动例题

第12章其他常用机构12-1棘轮机构除常用来实现间歇运动的功能外，还常用来实现什么功能？答：棘轮机构除了常用的间歇运动功能外，还能实现制动、进给、转位、分度、趙越运动等功能。

12-2某牛头刨床送进丝杠的导程为6mm,要求设计一棘轮机构，使每次送进呈可在0.2〜之间作有 级调整(共6级)。

设棘轮机构的棘爪由一曲柄摇杆机构的摇杆来推动，试绘出机构运动简图，并作必姜的计算 和说明。

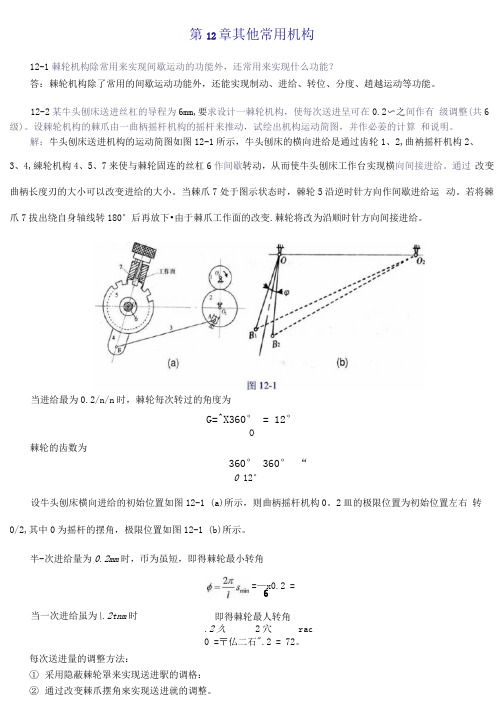
解：牛头刨床送进机构的运动简图如图12-1所示，牛头刨床的横向进给是通过齿轮1、2,曲衲摇杆机构2、 3、4,練轮机构4、5、7来使与棘轮固连的丝杠6作间歇转动，从而使牛头刨床工作台实现横向间接进给。

通过 改变曲柄长度刃的大小可以改变进给的大小。

当棘爪7处于图示状态时，棘轮5沿逆时针方向作间歇进给运 动。

若将棘爪7拔出绕自身轴线转180°后再放下•由于棘爪工作面的改变.棘轮将改为沿顺时针方向间接进给。

G=^X360° = 12°O棘轮的齿数为360° 360° “0 12°设牛头刨床横向进给的初始位置如图12-1 (a)所示，则曲柄摇杆机构0。

2皿的极限位置为初始位置左右 转0/2,其中0为摇杆的摆角，极限位置如图12-1 (b)所示。

半-次进给量为0.2mm 时，帀为虽短，即得棘轮最小转角.2久 2穴 rac0 =〒仏二石".2 = 72。

每次送进量的调整方法：① 采用隐蔽棘轮罩来实现送进駅的调格：② 通过改变棘爪摆角來实现送进就的调整。

当一次进给虽为\.2tnm 时 即得棘轮最人转角当进给最为0.2/n/n 时，棘轮每次转过的角度为=—x0.2 = 6图(a)中所示，三个楝爪尖在練轮齿圈上的位置相互磅个齿風图(b)中所示，三个棘爪尖在練轮齿圈上的位買相互差I个齿距。

(a) (b)图12-212-4当电钟电压不足时，为什么步进式电钟的秒针只在原地震荡，而不能作整周回转？答：如图12-3所示为用于电钟的棘轮机构。

一、牛头刨床机构的运动分析下图为一牛头刨床（Ⅲ级机构）。

假设已知各构件的尺寸如表2所示，原动件1以等角速度w1=1rad/s沿着逆时针方向回转，试求各从动件的角位移、角速度和角加速度以及刨头C点的位移、速度和加速度的变化情况。

二、牛头刨床机构的运动分析方程 1）位置分析建立封闭矢量多边形建立一直角坐标系，并标出各杆矢量及其方位角，其中共有4个未知量3θ（θ2=3θ）、4θ、3S 、5S 。

利用两个封闭图形ABDEFA 和EDCGE ，建立两个封闭矢量方程，由此可得：3125DE AB DE CD l s h h l l l h s →→→→→→→→→⎧+=++⎪⎨⎪+=+⎩(1)把（1）写成投影方程得：433214331143543cos *cos *cos *sin *sin *sin *cos *cos 0*sin *sin DE AB DE AB DE CD DE CD l s h l l s h l l l s l l h θθθθθθθθθθ*+=+⎫⎪+=+⎪⎬+-=⎪⎪+=⎭(2) 由以上各式用型转化法可求得4335s s θθ、、、，滑块2的方位角23θθ=2111*cos *sin b AB b AB x h l y h l θθ=+⎧⎨=+⎩ 44*cos *sin d DE d DE x l y l θθ=⎧⎨=⎩3s =3)*sin *()/*cos *(/c d CD d CD b d c d CD d CD b d s x x l x l x x s y y l y l y y s αα=+=+-⎧⎪⎨=+=+-⎪⎩ 3tan c dc dy y x x θ-=- 5c s x =()ae AE =44()tan *cos d c DE y h y l θθ+-=高斯消去法求解 2）速度分析对（2）求一次导数得：44333331144333331144334433*sin *s '*cos *sin **sin **cos *'*sin *cos **cos **sin **sin *0*cos **cos *0DE AB DE AB DE CD c DE CD l s l l s s l l l v l l θωθθωθωθωθθωθωθωθωθωθω-+-=-⎫⎪++=⎪⎬---=⎪⎪+=⎭(3)矩阵式：3334313334313443cos *sin *sin 0'*sin sin *cos *cos 0*cos 0*sin *sin 100*cos *cos 00DE AB DE AB CD DE CD DE c s l s l s l l l l l l v θθθθθθθθθθωθθ---⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥ω⎢⎥⎢⎥⎢⎥=ω1⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ (4)采用高斯消去法可求解（4）可解得角速度ω2,ω3; 3）加速度分析把(4)对时间求导数得：333433334334434cos *sin *sin 0''sin *cos *cos 00*sin *sin 10*cos *cos 0DE DE CD DE CD DE c s l s s l l l l l a θθθθθθθθαθθ--⎡⎤⎡⎤⎢⎥⎢⎥α⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎣⎦⎣⎦33333444433333343443334443344*sin '*sin **cos **cos 0'*cos '*cos **sin **sin 00**cos **cos 00**sin **sin 0DE DE CD DE CD DE c s s l s s s l l l l l v ωθθωθωθωθθωθωθωθωθωωθωθ----⎡⎤⎡⎤⎢⎥⎢⎥--ω⎢⎥⎢⎥=-⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦1111**cos **sin 00AB AB l l ωθωθ-⎡⎤⎢⎥-⎢⎥+ω1⎢⎥⎢⎥⎣⎦(5)采用高斯消去法可求解（5）可解得角加速度α2,α3,α5,α6三、程序流程图四、计算源程序#include<stdio.h>#include<stdlib.h>#include<math.h>/* 定义变量*/const double PI = 3.14159265358979;const int N = 4;const double EPSILON = 0.0001;const int T = 1000;/* 代入已知量*/double Lab=160,Lcd=1020,Lde=250,h=900,h1=460,h2=120,Omega1=1;/* 声明子函数*/void AngleDisplacement(double[12],double);/* 角位移函数*/void AngleVelocity(double[N][N],double[N],double[12],double);/* 角速度函数*/void AngleAcceleration(double[N][N],double[N][N],double[N],double [12]);/* 角加速度函数*/void GaussE(double [N][N],double [N],double [N]);/* 高斯消去法函数*/void ModulusMatrixA(double [12],double [N][N]);/* 矩阵A函数*/void ModulusMatrixB(double [12],double ,double [N]);/* 矩阵B函数*/void MatrixDA(double [12],double [N][N]);/* 矩阵DA函数*/void MatrixDB(double [12],double ,double [N]);/* 矩阵DB函数*//* 主函数*/void main(){int i,j;FILE *fp;double data[36][12];double value[12],a[N][N],da[N][N],b[N],db[N],Phi1;char flag;/* 打开文件*/if((fp = fopen("Data","w")) == NULL){printf("文件打开错误！\n");exit(0);}fprintf(fp,"Lab =%lf \n",Lab);fprintf(fp,"s3\tPhi3\tPhi4\ts5\t");fprintf(fp,"s3'\tOmega3\tOmega4\ts5'\t");fprintf(fp,"s3''\tEpsilon3\tEpsilon4\ts5''");printf("\n\n 牛头刨床机构运动分析程序\n\n\n");printf("\n");printf(" 是否开始计算(Y/N):");scanf("%c",&flag);if(flag =='Y'){/*计算并写入文件*/value[0] = 480;value[1] = 65 * PI / 180;value[2] = 10 * PI / 180;value[3] = 500;for(i = 0;i < 36; i++){Phi1 = i * PI / 18;AngleDisplacement(value,Phi1);ModulusMatrixB(value,Phi1,b);ModulusMatrixA(value,a);AngleVelocity(a,b,value,Phi1);MatrixDA(value,da);MatrixDB(value,Phi1,db);AngleAcceleration(a,da,db,value);for(j = 1;j < 3; j++)value[j] = value[j] * 180 / PI;for(j = 0;j < 12; j++)data[i][j] = value[j];fprintf(fp,"\n");for(j = 0;j < 12; j++)fprintf(fp,"%12.3f\t",data[i][j]);}fclose(fp);/* 输出数据*/printf("\n\n\n计算结果如下：\n");for(i = 0;i < 36; i++){Phi1=i * PI / 18;printf("\n输出Phi1=%d时的求解\n",i*10);printf(" S3 Phi3 Phi5 S5\n");for(j = 0;j < 4; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3' Omega3 Omega5S5'\n");for(j = 4;j < 8; j++)printf("%lf\t",data[i][j]);printf("\n");printf(" S3'' Epsilon3 Epsilon5 S5''\n");for(j = 8;j < 12; j++)printf("%lf\t",data[i][j]);printf("\n");}printf("\n程序运行结束，计算结果已写入Date文件中，请打开查看。

一：课程设计题目、内容及其目的课题：牛头刨床内容1．对机构进行运动分析已知：曲柄每分钟转数错误!未找到引用源。

,各构件尺寸及质心位置。

作机构1~2个位置的速度多边形和加速度多边形，作滑块的运动线图，以上内容与后面动态静力分析一起画在1号图纸上。

2．对机构进行动态静力分析已知：各构件的重量G（曲柄1、滑块2、和连杆5的重量都可以忽略不计），导杆3的转动惯量错误!未找到引用源。

及切削力错误!未找到引用源。

变化规律如下图。

确定构件一个位置的各运动副反力及应加于曲柄上的平衡力矩。

3、用UG进行模拟运动仿真校核机构运动分析和动态静力分析的结果4、电动机功率的确定与型号的选择5、齿轮减速机构设计目的：1：学会机械运动见图设计的步骤和方法；2：巩固所学的理论知识，掌握机构分析与综合的基本方法；3：培养学生使用技术资料，计算作图及分析与综合能力；4：培养学生进行机械创新的能力。

二：牛头刨床简介和机构的要求1：牛头刨床简介牛头刨床是一种用于平面切削加工的机床，如图1。

电动机经皮带和齿轮传动，经过减速机构减速从而带动曲柄1。

刨床工作时，由导杆3 经过连杆4 带动刨刀5 作往复运动。

刨头左行时，刨刀进行切削，称工作行程，此时要求速度较低并且均匀，以减少电动机容量和提高切削质量，刨头右行时，刨刀不切削，称空行程，此时要求速度较高，以提高生产率。

为此刨床采用有急回作用的导杆机构。

刨刀每切削完一次，利用空回行程的时间，通过棘轮带动螺旋机构（图中未画），使工作台连同工件作一次进给运动，以便刨刀继续切削。

刨头在工作行程中，受到很大的切削阻力（在切削的前后各有一段约0.05H 的空刀距离），而空回行程中只有摩擦阻力。

因此刨头在整个运动循环中，受力变化是很大的，这就影响了主轴的匀速运转，故需安装飞轮来减小主轴的速度波动，以提高切削质量和减小电动机容量。

2：机构的要求牛头刨床的主传动的从动机构是刨头，在设计主传动机构时，要满足所设计的机构要能使牛头刨床正常的运转，同时设计的主传动机构的行程要有急回运动的特性，刨削速度尽可能为匀速运动，以及很好的动力特性。

机械原理课程设计——牛头刨床(速度分析与受力分析附于最后)说明书姓名：分析点：4,10点组号：第3组2011 年 7 月 15日工作原理 (3)一.设计任务 (4)二.设计数据 (4)三.设计要求 (4)1、运动方案设计 (4)2、确定执行机构的运动尺寸 (4)3、进行导杆机构的运动分析 (5)4、对导杆机构进行动态静力分析 (5)四.设计方案选定 (5)五. 机构的运动分析 (6)1. 4点速度分析,加速度分析 (7)2. 10点速度,加速度分析 (9)六.机构动态静力分析 (11)七.数据总汇并绘图 (13)九.参考文献 (16)工作原理牛头刨床是一种用于平面切削加工的机床，如图a）所示。

电动机经过皮带和齿轮传动，带动曲柄2和固结在其上的凸轮8。

刨床工作时，由导杆机构2－3－4－5－6带动刨头6和刨刀7作往复运动。

刨头左行时，刨刀不切削，称为空回行程，此时要求速度较高，以提高生产率。

为此刨床采用有急回运动的导杆机构。

刨刀每切削完一次，利用空回行程的时间，凸轮8通过四杆机构1－9－10－11与棘轮带动螺旋机构（图中未画），使工作台连同工件作一次进给运动，以便刨刀继续切削。

刨头在工作过程中，受到很大的切削阻力（在切削的前后各有一段0.05H的空刀距离，见图b），而空回行程中则没有切削阻力。

因此刨头在整个运动循环中，受力变化是很大的，这就影响了主轴的匀速转动，故需安装飞轮来减小主轴的速度波动，以提高切削质量和减少电动机容量。

(a) (b)图d一.设计任务1、运动方案设计。

2、确定执行机构的运动尺寸。

3、进行导杆机构的运动分析。

4、对导杆机构进行动态静力分析。

5、汇总数据画出刨头的位移、速度、加速度线图以及平衡力矩的变化曲线。

二.设计数据本组选择第六组数据表1表2三.设计要求1、运动方案设计根据牛头刨床的工作原理，拟定1～2个其他形式的执行机构（连杆机构），给出机构简图并简单介绍其传动特点。

2、确定执行机构的运动尺寸根据表一对应组的数据，用图解法设计连杆机构的尺寸，并将设计结果和步骤写在设计说明书中。

设计题目：牛头刨床附图1：导杆机构的运动分析与动态静力分析附图2：齿轮机构的设计目录一.设计题目…………………………….……………………. .4二. 牛头刨床机构简介……………………………….………. .4三.机构简介与设计数据……………………………………. .. .5四. 设计内容…………….………………………….…………. .6五. 体会心得 (14)一、设计题目：牛头刨床1.）为了提高工作效率，在空回程时刨刀快速退回，即要有急回运动，行程速比系数在1.4左右。

2.）为了提高刨刀的使用寿命和工件的表面加工质量，在工作行程时，刨刀要速度平稳，切削阶段刨刀应近似匀速运动。

3.）曲柄转速在64r/min,刨刀的行程H在300mm左右为好，切削阻力约为9000N，其变化规律如图所示。

二、牛头刨床机构简介牛头刨床是一种用于平面切削加工的机床，如图4-1。

电动机经皮带和齿轮传动，带动曲柄2和固结在其上的凸轮8。

刨床工作时，由导杆机构2-3-4-5-6带动刨头6和刨刀7作往复运动。

刨头右行时，刨刀进行切削，称工作行程，此时要求速度较低并且均匀，以减少电动机容量和提高切削质量，刨头左行时，刨刀不切削，称空回行程，此时要求速度较高，以提高生产率。

为此刨床采用有急回作用的导杆机构。

刨刀每切削完一次，利用空回行程的时间，凸轮8通过四杆机构1-9-10-11与棘轮带动螺旋机构（图中未画），使工作台连同工件作一次进给运动，以便刨刀继续切削。

刨头在工作行程中，受到很大的切削阻力（在切削的前后各有一段约5H的空刀距离，见图4-1，b），而空回行程中则没有切削阻力。

因此刨头在整个运动循环中，受力变化是很大的，这就影响了主轴的匀速运转，故需安装飞轮来减小主轴的速度波动，以提高切削质量和减小电动机容量。

三、机构简介与设计数据3.1机构简介牛头刨床是一种用于平面切削加工的机床。

电动机经皮带和齿轮传动，带动曲柄2和固结在其上的凸轮8。

牛头刨床机构运动及动力分析编号：JYKS-JX-17-4-6**大学普通高等教育机械原理课程设计题目题号：牛头刨床机构运动及动力分析（C10）学院：机电工程学院专业班级：机械174学生姓名：**指导教师：**成绩：2020年7月1日目录课程设计题目、内容及其目的・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・1第1章机构简介与设计数据・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・21.1机构简介C10位置简图及原理・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・21.2・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・3第2章连杆分析・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・42.1连杆机构的运动分析・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・42.2对C10位置速度分析・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・42.3对C10位置加速度分析・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・52.4静力分析・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・7结论・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・10参考文献・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・11・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・12课程设计题目、内容及其目的题目牛头刨床机构运动及动力分析(C10)内容牛头刨床主传动机构运动简图设计及分析，计算牛头刨床主传动机构在指定位置的速度、加速度、受力，绘制机构运动简图、速度多边形、加速度多边形、受力分析图、力多边形，以上内容手绘在A1图纸上，并整理说明书。

目录一、概述1.1、课程设计的目的——————————————— 21.2、工作原理—————————————————— 21.3、设计要求—————————————————— 31.4、设计数据—————————————————— 41.5、创新设计内容及工作量———————————— 4二、牛头刨床主传动机构的结构设计与分析2.1、方案分析—————————————————— 52.2、主传动机构尺寸的综合与确定————————— 52.2、杆组拆分—————————————————— 62.4、绘制刀头位移曲线图————————————— 7三、牛头刨床主传动机构的运动分析及程序3.1、解析法进行运动分析————————————— 83.2、程序编写过程（计算机C语言程序）—————— 103.3、计算数据结果——————————————— 123.4、位移、速度和加速度运动曲线图与分析————— 13四、小结心得体会——————————————————— 18五、参考文献参考文献——————————————————— 19一、概述1.1、课程设计的目的目的：机械课程创新设计是培养学生机械系统方案设计能力的技术基础课程，他是机制专业课程学习过程中的一个重要实践环节。

其目的是以机制专业课程的学习为基础，进一步巩固和加深所学的基本理论、基本概念和基本知识，培养学生分析和解决与本专业课程有关的具体机械所涉及的实际问题的能力，使学生熟悉机械系统设计的步骤及方法，其中包括选型、运动方案的确定、运动学和动力学的分析和整体设计等，并进一步提高计算、分析、计算机辅助设计、绘图以及查阅和使用文献的综合能力。

1.2、工作原理牛头刨床是一种靠刀具的往复直线运动及工作台的间歇运动来完成工件的平面切削加工的机床。

图1为其参考示意图。

电动机经过减速传动装置（皮带和齿轮传动）带动执行机构（导杆机构和凸轮机构）完成刨刀的往复运动和间歇移动。

牛头刨床机械原理课程设计8’运动分析牛头刨床机械原理课程设计8’运动分析是指牛头刨床机械原理课程设计的八个主要运动分析方面的研究和分析。

它是机械学理论与牛头刨床机械原理课程设计中许多方面的一种综合性研究，不同于传统机械及机械控制相关的学科，有着自身独特的性质。

本文就牛头刨床机械原理课程设计8’运动分析进行深入分析，以期为工程设计和机械应用提供参考。

1、运动分析的基本概念运动分析是牛头刨床机械原理课程设计中必不可少的研究内容，其内容包括初始运动的准确分析、控制品的运动的动态分析、机械布置的结构分析、运动的变化情况分析以及牛头刨床机械原理的计算机仿真分析等。

运动分析的基本概念是以牛头刨床机械的物体及其相互关系为基础，分析运动物体间的动力学关系，求解物体运动的过程及参数，回答物体运动时所问的问题。

2、物体运动的速度分析物体运动的速度分析是牛头刨床机械原理课程设计中最重要的部分，它需要考虑物体的力学性质和运动参数，以及其相互的关系，并根据这些参数计算出物体运动的过程所需要的物理量和物理要素，以求得物体运动的最优结果。

通常情况下，需要考虑物体运动方向、运动状态、坐标系变换、时间演变等多种因素，并借助牛头刨床机械原理中的分析方法求解问题。

3、物体运动的动能分析物体运动的动能分析是指在牛头刨床机械原理课程设计中，通过分析物体运动的动能学分析，求解物体运动的动能学参数，其中包括物体的动能、力学活动能以及动能传递的几何关系等。

其目的是可以准确地预测和模拟物体运动时可能遇到的实际情况，从而有效地缩小物体运动的误差，进而提高物体控制的效果。

4、物体运动的静力分析物体运动的静力分析是指利用物体的坐标系变换、动量角度、力学活动能转移及各静力系统运行情况等，以及牛头刨床机械原理的物体运动模型，对物体的运动方式的静力特征进行考察和分析，求解物体运动的静力参数，从而获得物体运动的最佳结果。

5、牛头刨床机械原理计算机仿真牛头刨床机械原理计算机仿真是一种用于分析和模拟物体运动的计算机技术。