第4章 多元回归:估计与假设检验
- 格式:ppt
- 大小:1.29 MB
- 文档页数:24


第4章多元回归分析简单说,回归分析是根据统计资料建立经验公式的统计方法。
例如统计若干焊接点数据,从而建立由焊接点直径预报焊点剪切强度的预报公式;又如统计若干棵松树的胸径与材积(可利用木材体积),建立由胸径预报材积公式,也用到回归分析方法。
当然回归分析不只是建立预报公式,还要对预报误差的大小,预报公式的合理性等问题讨论,有着非常丰富的内容。
回归分析可用于预测和控制,在自然科学,社会科学和应用技术中都有重要应用,它是统计学最重要的工具。
回归分析方法和理论从Gauss提出最小二乘法开始,至今已近200年,目前仍在蓬勃发展,例如在回归诊断、维度缩减、半参数回归、非参数回归、LOGISTIC 回归等方向不断有新的突破。
本章介绍参数回归分析模型及其参数估计、检验、模型选择等理论和有关计算方法。
参数回归分析主要分三类:线性回归、可以转化为线性回归的回归和非线性回归。
本章依次介绍这三类模型。
有关回归分析的一般理论可参见陈希儒(1984),方开泰(1988),Seber(1976),何晓群(1997),何晓群、刘文卿(2001)、Richard(2003)。
Robert(1999)和王吉利(2004)提供了许多有趣的应用例子。
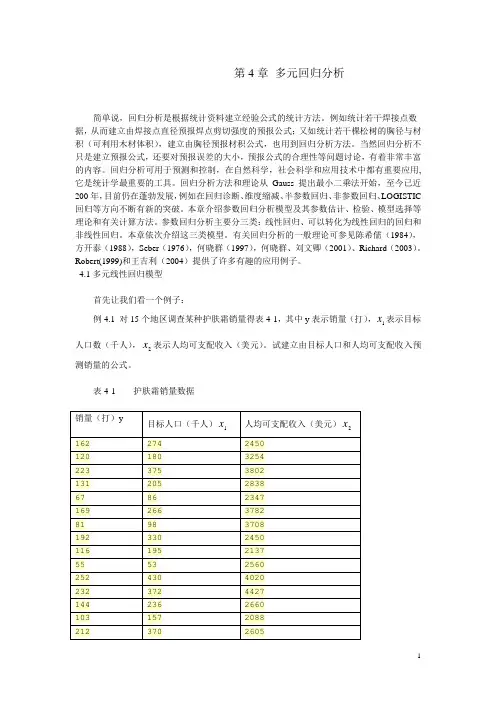
4.1多元线性回归模型首先让我们看一个例子:x表示目标例4.1 对15个地区调查某种护肤霜销量得表4-1,其中y表示销量(打),1x表示人均可支配收入(美元)。
试建立由目标人口和人均可支配收入预人口数(千人),2测销量的公式。
表4-1 护肤霜销量数据这个问题中,每个地区销量受该地区目标人口数和人均可支配收入数影响,3个变量y 、1x 、2x 间存在密切关系。
但是它们的关系不是确定性关系而是相关关系。
常见的变量间关系分为两大类:确定性关系和相关关系。
确定性关系也称为函数关系。
具有确定性关系时,自变量完全确定因变量的值。
例如存款的年利率c 固定,那么存款数z 与总利息y 的关系就是确定性关系;z 知道后,y 就由y=cz 确定。


多元统计分析第四章多元回归分析第4章多元回归分析简单说,回归分析是根据统计资料建⽴经验公式的统计⽅法。
例如统计若⼲焊接点数据,从⽽建⽴由焊接点直径预报焊点剪切强度的预报公式;⼜如统计若⼲棵松树的胸径与材积(可利⽤⽊材体积),建⽴由胸径预报材积公式,也⽤到回归分析⽅法。
当然回归分析不只是建⽴预报公式,还要对预报误差的⼤⼩,预报公式的合理性等问题讨论,有着⾮常丰富的内容。
回归分析可⽤于预测和控制,在⾃然科学,社会科学和应⽤技术中都有重要应⽤,它是统计学最重要的⼯具。
回归分析⽅法和理论从Gauss提出最⼩⼆乘法开始,⾄今已近200年,⽬前仍在蓬勃发展,例如在回归诊断、维度缩减、半参数回归、⾮参数回归、LOGISTIC 回归等⽅向不断有新的突破。
本章介绍参数回归分析模型及其参数估计、检验、模型选择等理论和有关计算⽅法。
参数回归分析主要分三类:线性回归、可以转化为线性回归的回归和⾮线性回归。
本章依次介绍这三类模型。
有关回归分析的⼀般理论可参见陈希儒(1984),⽅开泰(1988),Seber(1976),何晓群(1997),何晓群、刘⽂卿(2001)、Richard(2003)。
Robert(1999)和王吉利(2004)提供了许多有趣的应⽤例⼦。
4.1多元线性回归模型⾸先让我们看⼀个例⼦:x表⽰⽬标例4.1 对15个地区调查某种护肤霜销量得表4-1,其中y表⽰销量(打),1x表⽰⼈均可⽀配收⼊(美元)。
试建⽴由⽬标⼈⼝和⼈均可⽀配收⼊预⼈⼝数(千⼈),2测销量的公式。
表4-1 护肤霜销量数据这个问题中,每个地区销量受该地区⽬标⼈⼝数和⼈均可⽀配收⼊数影响,3个变量y 、1x 、2x 间存在密切关系。
但是它们的关系不是确定性关系⽽是相关关系。
常见的变量间关系分为两⼤类:确定性关系和相关关系。
确定性关系也称为函数关系。
具有确定性关系时,⾃变量完全确定因变量的值。
例如存款的年利率c 固定,那么存款数z 与总利息y 的关系就是确定性关系;z 知道后,y 就由y=cz 确定。

多元线性回归模型的公式和参数估计方法以及如何进行统计推断和假设检验多元线性回归模型是一种常用的统计分析方法,它在研究多个自变量与一个因变量之间的关系时具有重要的应用价值。
本文将介绍多元线性回归模型的公式和参数估计方法,并讨论如何进行统计推断和假设检验。
一、多元线性回归模型的公式多元线性回归模型的一般形式如下:Y = β0 + β1X1 + β2X2 + ... + βkXk + ε其中,Y表示因变量,X1至Xk表示自变量,β0至βk表示模型的参数,ε表示误差项。
在多元线性回归模型中,我们希望通过样本数据对模型的参数进行估计,从而得到一个拟合度较好的回归方程。
常用的参数估计方法有最小二乘法。
二、参数估计方法:最小二乘法最小二乘法是一种常用的参数估计方法,通过最小化观测值与模型预测值之间的残差平方和来估计模型的参数。
参数估计的公式如下:β = (X^T*X)^(-1)*X^T*Y其中,β表示参数矩阵,X表示自变量的矩阵,Y表示因变量的矩阵。
三、统计推断和假设检验在进行多元线性回归分析时,我们经常需要对模型进行统计推断和假设检验,以验证模型的有效性和可靠性。
统计推断是通过对模型参数的估计,来对总体参数进行推断。
常用的统计推断方法包括置信区间和假设检验。
1. 置信区间:置信区间可以用来估计总体参数的范围,它是一个包含总体参数真值的区间。
2. 假设检验:假设检验用于检验总体参数的假设是否成立。
常见的假设检验方法有t检验和F检验。
在多元线性回归模型中,通常我们希望检验各个自变量对因变量的影响是否显著,以及模型整体的拟合程度是否良好。
对于各个自变量的影响,我们可以通过假设检验来判断相应参数的显著性。
通常使用的是t检验,检验自变量对应参数是否显著不等于零。
对于整体模型的拟合程度,可以使用F检验来判断模型的显著性。
F检验可以判断模型中的自变量是否存在显著的线性组合对因变量的影响。
在进行假设检验时,我们需要设定显著性水平,通常是α=0.05。


第四章多元线性回归模型 在一元线性回归模型中,解释变量只有一个。但在实际问题中,影响因变量 的变量可能不止一个,比如根据经济学理论,人们对某种商品的需求不仅受该商 品市场价格的影响,而且受其它商品价格以及人们可支配收入水平的制约; 影响 劳动力劳动供给意愿(用劳动参与率度量)的因素不仅包括经济形势(用失业率 度量),而且包括劳动实际工资;根据凯恩斯的流动性偏好理论,影响人们货币 需求的因素不仅包括人们的收入水平, 而且包括利率水平等。当解释变量的个数 由一个扩展到两个或两个以上时,一元线性回归模型就扩展为多元线性回归模 型。本章在理论分析中以二元线性回归模型为例进行。 一、预备知识 (一)相关概念 对于一个三变量总体,若由基础理论,变量 x1, x2和变量y之间存在因果关 系,或xi,x2的变异可用来解释y的变异。为检验变量xi,x2和变量y之间因果关 系是否存在、度量变量 洛公2对变量y影响的强弱与显著性、以及利用解释变量 x「X2去预测因变量y,引入多元回归分析这一工具。 将给定xii, X2条件下y的均值 E(yi 区凶)J?。「Xi「2X2: (4.1)
定义为总体回归函数(Population Regression Function,PRF )。定义 % -E(yi |XiiXi)为误差项(error term ),记为叫,即叫二 yi - E(% |冷,X2J, 这样yi =E(% |心凶)*,或 yi = - 0 ■ - 1 X1i ■ - 2 X2i 川= (4.2 )
(4.2)式称为总体回归模型或者随机总体回归函数。其中,X1,X2称为解释 变量(explanatory variable ) 或自变量(independent variable ); y 称为被 解释变量(explained variable )或因变量(dependent variable );误差项」解 释了因变量的变动中不能完全被自变量所解释的部分。 在总体回归模型(4.2 )中参数r「1「2是未知的,7是不可观察的,统计 计量分析的目标之一就是估计模型的未知参数。给定一组随机样本 (yi , X1i , x2i ), i = 1,2,…,n,对(4.1 )式进行估计,若 E(yi | x1i , x2i), ■ 0, ■ 1, '2
