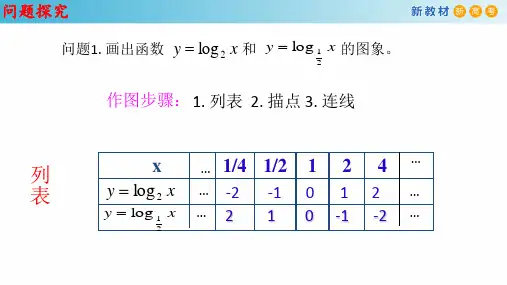
对数函数图象及性质——定义域值域

对数函数的定义与性质1. 定义对数函数是指可以将正实数映射到实数集上的函数。

常用的对数函数有自然对数函数和常用对数函数。

自然对数函数以数学常数e为底的对数函数，通常以ln(x)表示，其中x为正实数。

常用对数函数以10为底的对数函数，通常以log(x)表示，其中x为正实数。

2. 性质2.1 对数函数的定义域和值域自然对数函数ln(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

常用对数函数log(x)的定义域是正实数集(0, +∞)，值域是实数集(-∞, +∞)。

2.2 对数函数的性质（1）对数函数的图像：自然对数函数ln(x)和常用对数函数log(x)的图像都是单调递增的曲线。

（2）基本性质：对数函数具有以下基本性质：•ln(1) = 0，即自然对数函数ln(x)在x=1处的函数值为0。

•ln(e) = 1，即自然对数函数ln(x)在x=e处的函数值为1。

•log(1) = 0，即常用对数函数log(x)在x=1处的函数值为0。

•log(10) = 1，即常用对数函数log(x)在x=10处的函数值为1。

（3）对数函数的性质：对数函数具有以下性质：•ln(x y) = ln(x) + ln(y)，即自然对数函数ln(x y)等于自然对数函数ln(x)和ln(y)的和。

•ln(x/y) = ln(x) - ln(y)，即自然对数函数ln(x/y)等于自然对数函数ln(x)和ln(y)的差。

•ln(x^n) = n * ln(x)，即自然对数函数ln(x^n)等于n乘以自然对数函数ln(x)。

•log(x y) = log(x) + log(y)，即常用对数函数log(x y)等于常用对数函数log(x)和log(y)的和。

•log(x/y) = log(x) - log(y)，即常用对数函数log(x/y)等于常用对数函数log(x)和log(y)的差。

•log(x^n) = n * log(x)，即常用对数函数log(x^n)等于n乘以常用对数函数log(x)。

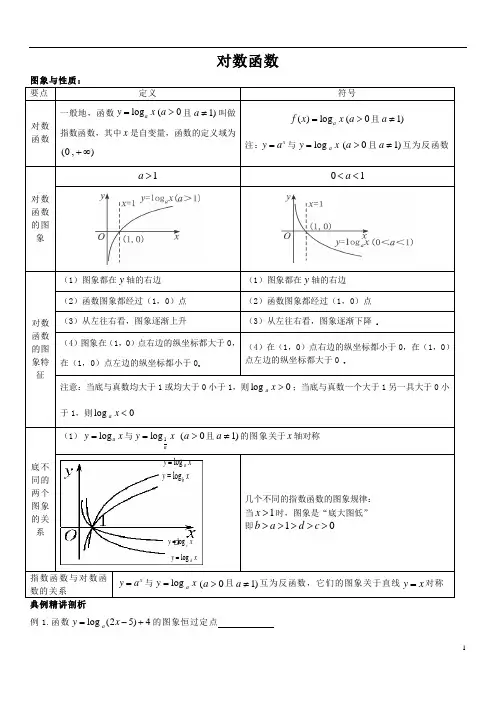
对数函数 图象与性质：要点 定义 符号对数函数 一般地，函数log (0a y x a =>且1)a ≠叫做指数函数，其中x 是自变量，函数的定义域为(0,)+∞ ()log (0a f x x a =>且1)a ≠ 注：xy a =与log a y x =(0a >且1)a ≠互为反函数对数函数的图象1a > 01a <<对数函数的图象特征（1）图象都在y 轴的右边 （1）图象都在y 轴的右边（2）函数图象都经过（1，0）点 （2）函数图象都经过（1，0）点 （3）从左往右看，图象逐渐上升 （3）从左往右看，图象逐渐下降 . （4）图象在（1，0）点右边的纵坐标都大于0，在（1，0）点左边的纵坐标都小于0. （4）在（1，0）点右边的纵坐标都小于0，在（1，0）点左边的纵坐标都大于0 . 注意：当底与真数均大于1或均大于0小于1，则log 0a x >；当底与真数一个大于1另一具大于0小于1，则log 0a x <底不同的两个图象的关系 （1）log a y x =与1log ay x =(0a >且1)a ≠的图象关于x 轴对称几个不同的指数函数的图象规律： 当1x >时，图象是“底大图低” 即10b a d c >>>>>指数函数与对数函数的关系 x y a =与log a y x =(0a >且1)a ≠互为反函数，它们的图象关于直线y x =对称 典例精讲剖析例1.函数log (25)4a y x =-+的图象恒过定点log a y x=log b y x=log c y x=log d y x =例 2. 已知()f x 是对函数xy a =(0a >且1)a ≠的反函数，并且()f x 的图象经过1(3,)2P ，求3()3f 的值例3. 求下列函数的定义域：（1）2log a y x = (2)log (42)a y x =- （3）(1)log (164)x x y +=-例4. 求函数2()log ||f x x =的定义域，并画出它的图象.练习：1.下列函数是对数函数的是( ) A ．2log a y x =(0a >且1)a ≠ B. 1log 2a y x =(0a >且1)a ≠ C ．2log a y x =(0a >且1)a ≠ D ．log ||a y x =(0a >且1)a ≠2. 已知0a >且1a ≠，函数x y a =与log ()a y x =-的图象只能是 ( )3. 如下图所示的曲线是对数函数y ＝log a x 的图象，已知a 的取值分别为43、3、110、35，则相应于C 1、C 2、C 3、C 4的a 值依次是4. 已知()f x 是对数函数，且()f x 的图象过点(27,6)P -，求()f x 的解析式5. 求下列函数的定义域：（1）2()log (21)f x x =- (2) 121()log (32)f x x =- （3）41()log (32)f x x =--基础知识：对数函数的图象和性质函数名称 指数函数解析式 ()log (0a f x x a =>且1)a ≠ 定义域 (0,)+∞值域 (,)-∞+∞，图象1a > 01a <<性质奇偶性 对数函数是非奇非偶函数单调性 在(0,)+∞上是增函数 在(0,)+∞上是减函数 函数值分布 0(1)log 0(1)1(01)a x x x x >>⎧⎪==⎨⎪<<<⎩ 0(1)log 0(1)0(01)a x x x x <>⎧⎪==⎨⎪><<⎩典例精讲剖析例1. 比较下列各组数中两个值的大小：（1）2log 3.4，2log 3.8； （2）05log 1.8，05log 2.1；（3）log 5.1a ，log 5.9a （0a >，1a ≠）； （4）7log 5，6log 7；（5） 2.10.3，0.312，2log 0.3； （6）0.7log 0.8， 1.1log 0.9，0.91.1例2. 解下列不等式：（1）33log (21)log (52)x x ->- （2）0.30.3log (35)log (27)x x -≥+例3.若3log 14a <（0a >，1a ≠），求实数a 的取值范围.例4.已知函数23()log (87)f x x x =-+-，求函数()f x 的定义域与值域练习：1. 设a ＝log 3π，b ＝log 23，c ＝log 32，则( )A ．a >b >cB ．a >c >bC ．b >a >cD ．b >c >a2. 已知集合{2|log ,1}A y y x x ==>，1{|(),1}2x B y y x ==>，则A B =() A ．1{|0}2y y << B ．{|0}y y > C ．Φ D ．R3.函数y =定义域为( ) A.3(,1)4 B. 3(,)4+∞ C ．(1,)+∞ D. 3(,1)(1,)4+∞4. 若3log 14a >（0a >，1a ≠），求实数a 的取值范围.5. 已知0.70.7log (2)log (1)m m <-，求m 的取值范围6. 判断函数21()log 1xf x x +=-的奇偶性。

对数函数的图像与性质对数函数是数学中非常重要的一类函数，它在各个领域中都有着广泛的应用。

本文将着重探讨对数函数的图像和性质，帮助读者更好地理解和应用对数函数。

一、对数函数的定义与基本性质对数函数的定义如下：定义：设a为正实数且不等于1，x为正实数，那么以a为底的对数函数y = loga x 定义为x = a^y。

对数函数的图像在直角坐标系中呈曲线状，其主要性质如下：1. 定义域与值域：对数函数的定义域为正实数集合，值域为实数集合。

2. 特殊性质：当x = 1 时，对数函数的值为0，即loga 1 = 0。

3. 单调性：当0 < a < 1 时，对数函数随着x的增大而递减；当a > 1 时，对数函数随着x的增大而递增。

4. 对称性：对数函数在y轴上有一个对称中心O(1,0)。

以上是对数函数的基本性质，接下来我们将进一步探讨对数函数的图像。

二、对数函数的图像特点对数函数的图像在直角坐标系中呈现出一些特殊的特点，我们将分别从底数的大小和常数c的引入的平移和伸缩等方面进行讨论。

1. 底数的大小对图像的影响底数a的大小对对数函数的图像有显著的影响。

当0 < a < 1 时，对数函数的图像在一象限内，从左上方无穷递减到右下方；当a > 1 时，对数函数的图像在一、三象限内，从左下方无穷递增到右上方。

2. 平移和伸缩对图像的影响引入常数c对对数函数的图像进行平移和伸缩。

当常数c大于0时，对数函数的图像在x轴的正方向上平移c个单位；当常数c小于0时，对数函数的图像在x轴的负方向上平移|c|个单位。

另外，对数函数的图像近似于一条曲线，它的凹性和凸性取决于底数的大小。

当0 < a < 1 时，对数函数图像凸向下；当a > 1 时，对数函数图像凹向下。

三、对数函数在实际问题中的应用对数函数在各个领域中都有着广泛的应用。

以下是一些常见的实际问题：1. 指数增长问题：对数函数可以用来描述指数增长的问题，例如人口增长、物种扩散等。

对数函数在数学的浩瀚星空中，对数函数犹如一颗璀璨的星辰，它不仅连接了算术与指数的桥梁，更是解决实际问题、深化数学理解的强大工具。

对于正步入高中学习阶段、怀揣着对未知世界好奇与探索欲望的你们而言，掌握对数函数，无疑是开启数学新纪元的一把钥匙。

本文将带领大家一同走进对数函数的奇妙世界，从基础概念出发，逐步探索其性质、应用及与高考的紧密联系。

一、对数的背景在探讨对数函数之前，让我们先回顾一下它的起源。

对数，这一概念的诞生，源自对复杂运算简化的渴望。

17世纪初，苏格兰工程师约翰·纳皮尔发明了对数，用以简化天文计算中的乘法与除法运算，使之转化为加法与减法，极大地提高了计算效率。

二、对数的概念如果），＞（1a 0a a x≠=N ，即a 的x 次方等于N （a>0，且a≠1），那么数x 叫做以a 为底N 的对数（logarithm ），记作x=logₐN 。

其中，a 叫做对数的底数，N 叫做真数，x 叫做“以a 为底N 的对数”。

注意：1、负数和零没有对数2、），且＞（1a 0a 01log 1a a 0≠=⇔=3、我们将以10为底的对数叫做常用对数，并把logₐN 记作lgN ，以无理数e=2.71828........为底的对数叫做自然对数，并把logₐN 记作lnN 三、对数的运算性质1、N M MN a a a log log log +=）（2、N M NM a a a log log log -=3、MM a n a nlog log =4、对数的换低公式：），且＞；＞；，且＞（1c 0c 0b 1a 0a alog b log b log c c a ≠≠=四、对数函数的定义一般地，函数y=logₐx（a>0，且a≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数五、对数函数的图象及性质1、对数函数的图象当a>1时当0<a<1时2.定义域与值域：对于对数函数y=logₐx（a>0且a≠1），其定义域是(0,+∞)，值域为R3.单调性：对数函数的单调性与其底数a密切相关。