2020版高考新创新一轮复习数学理科通用版课时跟踪检测三十四数列求和含答案

第34讲 等差数列及其前n 项和夯实基础 【p 73】【学习目标】1．掌握等差数列的定义与性质、通项公式、前n 项和公式等． 2．掌握等差数列的判断方法． 3．掌握等差数列求和的方法． 【基础检测】1．数列{a n }是等差数列，a 1＝1，a 4＝8，则a 5＝( )A ．16B ．－16C ．32D .313【解析】因为a 4＝8，所以a 1＋3d ＝8， 又因为a 1＝1，所以d ＝73，可得a 5＝a 1＋4d ＝313.【答案】D2．已知等差数列{a n }中，若a 4＝15，则它的前7项和为( )A ．120B ．115C ．110D ．105【解析】由题得S 7＝72(a 1＋a 7)＝72·2a 4＝7a 4＝7×15＝105.【答案】D3．在数列{a n }中，若a 1＝1，a 2＝12，2a n ＋1＝1a n ＋1a n ＋2(n∈N *)，则该数列的通项为( )A ．a n ＝1nB ．a n ＝2n ＋1C ．a n ＝2n ＋2D ．a n ＝3n【解析】由2a n ＋1＝1a n ＋1a n ＋2可得1a n ＋1－1a n ＝1a n ＋2－1a n ＋1，知⎩⎨⎧⎭⎬⎫1a n 是首项为1a 1＝1，公差为1a 2－1a 1＝2－1＝1的等差数列，所以1a n＝n ，即a n ＝1n.【答案】A4．记S n 为等差数列{}a n 的前n 项和，若S 9＝45，a 3＋a 8＝12，则a 7等于( ) A ．10 B ．9 C ．8 D ．7【解析】S 9＝9a 5＝45a 5＝5，而a 3＋a 8＝12a 5＋a 6＝12，a 6＝7. ∵2a 6＝a 5＋a 7，∴a 7＝9. 【答案】B5．设等差数列{a n }的前n 项和为S n ，若a 1＝－11, a 3＋a 7＝－6，则当S n 取得最小值时，n 等于( )A ．6B ．7C ．8D ．9【解析】由题设⎩⎪⎨⎪⎧a 1＝－112a 1＋8d ＝－6d ＝2，则S n ＝n 2＋(－11－1)n ＝n 2－12n ，所以当n ＝6时，S n ＝n 2－12n 最小．【答案】A 【知识要点】 1．等差数列的定义一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫做等差数列，这个常数叫做等差数列的公差，通常用字母__d__表示．2．等差数列的通项公式如果等差数列{a n }的首项为a 1，公差为d ，那么它的通项公式是a n ＝a 1＋(n －1)d (n∈N *)． 3．等差中项如果A ＝a ＋b 2，那么A 叫做a 与b 的等差中项．4．等差数列的常用性质(1)通项公式的推广：a n ＝a k ＋(n －k)d(n ，k ∈N *)．(2)若{a n }为等差数列，且m ＋n ＝p ＋q (m ，n ，p ，q ∈N *)，则a m ＋a n ＝a p ＋a q . (3)若{a n }是等差数列，公差为d ，则a n ，a n ＋m ，a n ＋2m ，…(n ，m ∈N *)是公差为__md __的等差数列．(4)数列S m ，S 2m －S m ，S 3m －S 2m ，…也是等差数列． 5．等差数列的前n 项和公式设等差数列{a n }的公差为d ，其前n 项和S n ＝n （a 1＋a n ）2或S n ＝na 1＋n （n －1）2d(n∈N *)．6．等差数列的前n 项和公式与函数的关系 S n ＝d 2n 2＋⎝⎛⎭⎪⎫a 1－d 2n(n∈N *)．数列{a n }是等差数列S n ＝An 2＋Bn (A 、B 为常数，n ∈N *)． 7．等差数列的前n 项和的最值在等差数列{a n }中，若a 1>0，d<0，则S n 存在最__大__值；若a 1<0，d>0，则S n 存在最__小__值．典例剖析 【p 73】考点1 等差数列基本量的计算例1(1)已知等差数列共有10项，其中奇数项之和为15，偶数项之和为30，则其公差是( )A ．5B ．4C ．3D ．2【解析】写出数列的第一、三、五、七、九项的和，写出数列的第二、四、六、八、十项的和，都用首项和公差表示，两式相减，得到结果．由此得：⎩⎪⎨⎪⎧5a 1＋20d ＝155a 1＋25d ＝30d ＝3.【答案】C(2)已知数列{a n }为等差数列，S n 为其前n 项和，a 7－a 5＝4，a 11＝21，S k ＝9，则k ＝________． 【解析】a 7－a 5＝2d ＝4，d ＝2，a 1＝a 11－10d ＝21－20＝1， S k ＝k ＋k （k －1）2×2＝k 2＝9.又k∈N *，故k ＝3.【答案】3【点评】在求解等差数列的基本量问题中主要使用的是方程思想，要注意公式使用时的准确性与合理性，更要注意运算的准确性．在遇到一些较复杂的方程组时，要注意整体代换思想的运用，使运算更加简捷． 考点2 等差数列的性质及应用例2(1)在等差数列{a n }中，a 3＋a 9＝27－a 6，S n 表示数列{a n }的前n 项和，则S 11＝( ) A ．18 B ．99 C ．198 D ．297【解析】因为a 3＋a 9＝27－a 6，2a 6＝a 3＋a 9，所以3a 6＝27，所以a 6＝9，所以S 11＝112(a 1＋a 11)＝11a 6＝99.【答案】B(2)已知{a n }为等差数列，若a 1＋a 2＋a 3＝5，a 7＋a 8＋a 9＝10，则a 19＋a 20＋a 21＝________． 【解析】法一：设数列{a n }的公差为d ，则a 7＋a 8＋a 9＝a 1＋6d ＋a 2＋6d ＋a 3＋6d ＝5＋18d ＝10，所以18d ＝5，故a 19＋a 20＋a 21＝a 7＋12d ＋a 8＋12d ＋a 9＋12d ＝10＋36d ＝20.法二：由等差数列的性质，可知S 3，S 6－S 3，S 9－S 6，…，S 21－S 18成等差数列，设此数列公差为D.所以5＋2D ＝10，所以D ＝52.所以a 19＋a 20＋a 21＝S 21－S 18＝5＋6D ＝5＋15＝20.【答案】20【点评】一般地，运用等差数列性质，可以化繁为简、优化解题过程．但要注意性质运用的条件，如m ＋n ＝p ＋q ，则a m ＋a n ＝a p ＋a q (m ，n ，p ，q ∈N *)，只有当序号之和相等、项数相同时才成立．考点3 等差数列的判定与证明例3令 b n ＝2n ⎝ ⎛⎭⎪⎫n －12n ＋c ，数列{b n }为等差数列，则非零常数c 的值为________．【解析】∵b n ＝2n ⎝ ⎛⎭⎪⎫n －12n ＋c，c ≠0，数列{b n }为等差数列，∴b n ＝2n.得到c ＝－12.【答案】－12例4已知数列{a n }满足a 1＝1，a n ＋1＝2a n a n ＋2(n∈N )，b n ＝1a n .(1)证明：数列{b n }为等差数列． (2)求数列{a n }的通项公式．【解析】(1)∵a 1≠0，且有a n ＋1＝2a n a n ＋2，所以有a n ≠0(n ∈N *)，则有b n ＋1＝1a n ＋1＝a n ＋22a n＝1 a n ＋12＝b n＋12，即b n＋1－b n＝12(n∈N*)且b1＝1a1＝1，所以{b n}是首项为1，公差为12的等差数列．(2)由(1)知b n＝b1＋(n－1)×12＝1＋n－12＝n＋12，即1a n＝n＋12，所以a n＝2n＋1.【点评】等差数列的判定与证明方法－1(n≥2，n∈N*)为同一常数{a n}{a n}是等差数列正整数n都成立{a n}是等差数任意的正整数n 都成立{a n }是考点4 等差数列前n 项和的最值问题例5已知{a n }是各项为正数的等差数列，S n 为其前n 项和，且4S n ＝(a n ＋1)2. (1)求a 1，a 2的值及{a n }的通项公式； (2)求数列⎝ ⎛⎭⎪⎫S n －72a n 的最小值． 【解析】(1)因为4S n ＝(a n ＋1)2，所以，当n ＝1时，4a 1＝(a 1＋1)2，解得a 1＝1，所以，当n ＝2时，4(1＋a 2)＝(a 2＋1)2，解得a 2＝－1或a 2＝3， 因为{a n }是各项为正数的等差数列，所以a 2＝3， 所以{a n }的公差d ＝a 2－a 1＝2，所以{a n }的通项公式a n ＝a 1＋(n －1)d ＝2n －1. (2)因为4S n ＝(a n ＋1)2，所以S n ＝（2n －1＋1）24＝n 2，所以S n －72a n ＝n 2－72(2n －1)＝n 2－7n ＋72＝⎝ ⎛⎭⎪⎫n －722－354.所以，当n ＝3或n ＝4时，S n －72a n 取得最小值－172.方法总结 【p 74】1．等差数列的判定方法有定义法、中项公式法、通项公式法、前n 项和公式法，注意等差数列的证明只能用定义法．2．方程思想和基本量思想：在解有关等差数列问题时可以考虑化归为首项与公差等基本量，通过建立方程组获得解．3．用函数思想理解等差数列的通项公式和前n 项和公式，从而解最值问题．走进高考 【p 74】1．(2018·全国卷Ⅰ)设S n 为等差数列{a n }的前n 项和．若3S 3＝S 2＋S 4，a 1＝2，则a 5＝( )A ．－12B ．－10C ．10D ．12【解析】法一：设等差数列{a n }的公差为d ，∵3S 3＝S 2＋S 4， ∴3⎝ ⎛⎭⎪⎫3a 1＋3×22d ＝2a 1＋d ＋4a 1＋4×32d ，解得d ＝－32a 1， ∵a 1＝2，∴d ＝－3，∴a 5＝a 1＋4d ＝2＋4×(－3)＝－10.法二：设等差数列{a n }的公差为d ，∵3S 3＝S 2＋S 4，∴3S 3＝S 3－a 3＋S 3＋a 4，∴S 3＝a 4－a 3，∴3a 1＋3×22d ＝d ，∵a 1＝2，∴d ＝－3，∴a 5＝a 1＋4d ＝2＋4×(－3)＝－10.【答案】B2．(2018·全国卷Ⅱ)记S n 为等差数列{a n }的前n 项和，已知a 1＝－7，S 3＝－15. (1)求{a n }的通项公式； (2)求S n ，并求S n 的最小值．【解析】(1)设{a n }的公差为d ，由题意得3a 1＋3d ＝－15.由a 1＝－7得d ＝2.所以{a n }的通项公式为a n ＝2n －9. (2)由(1)得S n ＝n 2－8n ＝(n －4)2－16.所以当n ＝4时，S n 取得最小值，最小值为－16.考点集训 【p 214】A 组题1．在等差数列{a n }中，a 1＝0，公差d ≠0，若a m ＝a 1＋a 2＋…＋a 9，则m 的值为( ) A ．37 B ．36 C ．20 D ．19【解析】a m ＝a 1＋a 2＋…＋a 9＝9a 1＋9×82d ＝36d ＝a 37.【答案】A2．记S n 为等差数列{}a n 的前n 项和，若a 7＝1，a 1－S 4＝9，则数列{}S n 中的最小项为( )A ．S 1B ．S 5，S 6C ．S 4D ．S 7【解析】令等差数列{}a n 的公差为d ，则⎩⎪⎨⎪⎧a 1＋6d ＝1，a 1－4a 1－6d ＝9，解得a 1＝－5，d ＝1，有a n ＝n －6，S n ＝n （n －11）2，则当n ＝5或6时，S n 最小．【答案】B3．已知数列{a n }满足a 1＝15，且3a n ＋1＝3a n －2.若a k ·a k ＋1<0，则正整数k ＝( ) A ．21 B ．22 C ．23 D ．24【解析】3a n ＋1＝3a n －2a n ＋1＝a n －23{a n }是等差数列，则a n ＝473－23n .∵a k ·a k ＋1<0，∴⎝⎛⎭⎪⎫473－23k ⎝ ⎛⎭⎪⎫453－23k <0，∴452<k <472，∴k ＝23.【答案】C4．设{a n }(n ∈N *)是等差数列，S n 是其前n 项的和，且S 5＜S 6，S 6＝S 7＞S 8，则下列结论错误．．的是( ) A. d ＜0 B. a 7＝0 C. S 9＞S 5D. S 6与S 7均为S n 的最大值【解析】由S 5<S 6得a 6＝S 6－S 5>0，又S 6＝S 7，所以a 7＝0. 由S 7>S 8，得a 8<0，而C 选项S 9>S 5，即a 6＋a 7＋a 8＋a 9>02(a 7＋a 8)>0.由题设a 7＝0，a 8<0，显然C 选项是错误的． 【答案】C5．设S n 为等差数列{a n }的前n 项和，若S 8＝4a 3，a 7＝－2，则a 9＝________． 【解析】根据等差数列的定义和性质可得，S 8＝4(a 3＋a 6)，又S 8＝4a 3，所以a 6＝0，又a 7＝－2，所以a 8＝－4，a 9＝－6. 【答案】－66．设等差数列{a n }的前n 项和为S n ，S m －1＝－2，S m ＝0，S m ＋1＝3，则正整数m 的值为________． 【解析】因为等差数列{a n }的前n 项和为S n ，S m －1＝－2，S m ＝0，S m ＋1＝3，所以a m ＝S m－S m －1＝2，a m ＋1＝S m ＋1－S m ＝3，数列的公差d ＝1，a m ＋a m ＋1＝S m ＋1－S m －1＝5，即2a 1＋2m －1＝5，所以a 1＝3－m .由S m ＝(3－m )m ＋m （m －1）2×1＝0，解得正整数m 的值为5.【答案】57．已知等差数列{a n }的公差d ＞0.设{a n }的前n 项和为S n ，a 1＝1，S 2·S 3＝36.(1)求d 及S n ；(2)求m ，k (m ，k ∈N *)的值，使得a m ＋a m ＋1＋a m ＋2＋…＋a m ＋k ＝65.【解析】(1)由题意知(2a 1＋d )(3a 1＋3d )＝36，将a 1＝1代入上式解得d ＝2或d ＝－5. 因为d ＞0，所以d ＝2.从而a n ＝2n －1，S n ＝n 2(n ∈N *)．(2)由(1)得a m ＋a m ＋1＋a m ＋2＋…＋a m ＋k ＝(2m ＋k －1)(k ＋1)，所以(2m ＋k －1)(k ＋1)＝65.由m ，k ∈N *知2m ＋k －1≥k ＋1＞1，故⎩⎪⎨⎪⎧2m ＋k －1＝13，k ＋1＝5，所以⎩⎪⎨⎪⎧m ＝5，k ＝4. 8．已知等差数列{a n }前三项的和为－9，前三项的积为－15.(1)求等差数列{a n }的通项公式；(2)若{a n }为递增数列，求数列{|a n |}的前n 项和S n .【解析】(1)设公差为d ，则依题意得a 2＝－3，则a 1＝－3－d ，a 3＝－3＋d ，∴(－3－d )(－3)(－3＋d )＝－15，得d 2＝4，d ＝±2，∴a n ＝－2n ＋1或a n ＝2n －7.(2)由题意得a n ＝2n －7，所以|a n |＝⎩⎪⎨⎪⎧7－2n ，n ≤3，2n －7，n ≥4， ①n ≤3时，S n ＝－(a 1＋a 2＋…＋a n )＝5＋（7－2n ）2n ＝6n －n 2； ②n ≥4时，S n ＝－a 1－a 2－a 3＋a 4＋…＋a n ＝－2(a 1＋a 2＋a 3)＋(a 1＋a 2＋…＋a n )＝18－6n ＋n 2.综上，数列{|a n |}的前n 项和S n ＝⎩⎪⎨⎪⎧－n 2＋6n ，n ≤3，n 2－6n ＋18，n ≥4. B 组题1．已知正项数列{a n }中，a 1＝1, a 2＝2, 2a 2n ＋1＝a 2n ＋2＋a 2n ，则a 6等于( )A ．16B ．8C ．4D ．2 2【解析】由2a 2n ＋1＝a 2n ＋2＋a 2n 知，数列{a 2n }是等差数列，前两项为1，4，所以公差d ＝3，故a 26＝1＋5×3＝16，所以a 6＝4，故选C.【答案】C2．若等差数列{a n }的前n 项和S n 满足S 4≤4，S 6≥12，则a 4的最小值为( )A ．2 B.72C ．3 D.52【解析】S 4＝2(a 1＋a 4)≤42a 4－3d ≤2，① S 6＝3(a 1＋a 6)≥122a 4－d ≥4，即d －2a 4≤－43d －6a 4≤－12，②①②两式相加得：a 4≥52. 【答案】D3．设数列{a n }满足a 1＝2，a 2＝6，且a n ＋2－2a n ＋1＋a n ＝2，用[x ]表示不超过x 的最大整数，如[0.6]＝0，[1.2]＝1，则⎣⎢⎡⎦⎥⎤m a 1＋m a 2＋…＋m a m 的值用m (m 为整数)表示为__________． 【解析】由题设可得(a n ＋2－a n ＋1)－(a n ＋1－a n )＝2，令b n ＝a n ＋1－a n ，则由等差数列的定义可知数列{}b n 是首项为b 1＝a 2－a 1＝4，公差为d ＝2的等差数列，即a n ＋1－a n ＝4＋2(n －1)＝2n ＋2，由此可得a 2－a 1＝2×1＋2，a 3－a 2＝2×2＋2，…，a n －a n －1＝2(n －1)＋2，将以上(n －1)个等式两边相加可得a n －a 1＝2×（1＋n －1）2(n －1)＋2n －2＝n (n －1)＋2n －2，即a n ＝n (n ＋1)，所以m a 1＋m a 2＋…＋m a m ＝m －m 2＋m 2－m 3＋…＋m m －1－m m ＝m －1，故⎣⎢⎡⎦⎥⎤m a 1＋m a 2＋…＋ma m＝m －1.【答案】m －14．设数列{a n }的前n 项和为S n ，4S n ＝a 2n ＋2a n －3，且a 1，a 2，a 3，a 4，a 5成等比数列，当n ≥5时，a n >0.(1)求证：当n ≥5时，{a n }成等差数列；(2)求{a n }的前n 项和S n .【解析】(1)由4S n ＝a 2n ＋2a n －3，4S n ＋1＝a 2n ＋1＋2a n ＋1－3，得4a n ＋1＝a 2n ＋1－a 2n ＋2a n ＋1－2a n ， 即(a n ＋1＋a n )(a n ＋1－a n －2)＝0. 当n ≥5时，a n >0，所以a n ＋1－a n ＝2， 所以当n ≥5时，{a n }成等差数列．(2)由4a 1＝a 21＋2a 1－3，得a 1＝3或a 1＝－1，又a 1，a 2，a 3，a 4，a 5成等比数列， 而a 5>0，所以a 1>0，从而a 1＝3， 所以a n ＋1＋a n ＝0(n ≤5)，q ＝－1，所以a n ＝⎩⎪⎨⎪⎧3（－1）n －1，1≤n ≤4，2n －7，n ≥5， 所以S n ＝⎩⎪⎨⎪⎧32[1－（－1）n ]，1≤n ≤4，n 2－6n ＋8，n ≥5.。

课时跟踪检测（三十一） 数列求和一抓基础，多练小题做到眼疾手快1．(2019·镇江调研)已知{}a n 是等差数列，S n 为其前n 项和，若a 3＋a 7＝8，则S 9＝_______.解析：在等差数列{}a n 中，由a 3＋a 7＝8， 得a 1＋a 9＝8， 所以S 9＝a 1＋a 9×92＝8×92＝36.答案：36 2．数列{1＋2n －1}的前n 项和为________．解析：由题意得a n ＝1＋2n －1，所以S n ＝n ＋1－2n1－2＝n ＋2n－1.答案：n ＋2n－13．数列{a n }的通项公式是a n ＝(－1)n(2n －1)，则该数列的前100项之和为________． 解析：根据题意有S 100＝－1＋3－5＋7－9＋11－…－197＋199＝2×50＝100. 答案：1004．(2018·泰州期末)已知数列{}a n 的通项公式为a n ＝n ·2n －1，前n 项和为S n ，则S n ＝________.解析：∵a n ＝n ·2n －1，∴S n ＝1×1＋2×2＋3×22＋…＋n ×2n －1，2S n ＝1×2＋2×22＋3×23＋…＋n ×2n， 两式相减可得－S n ＝1＋2＋22＋…＋2n －1－n ·2n＝1－2n1－2－n ·2n，化简可得S n ＝(n －1)2n＋1. 答案：(n －1)2n＋15．已知等比数列{}a n 的公比q ＞1，且a 5－a 1＝30，a 4－a 2＝12，则数列⎩⎨⎧⎭⎬⎫a na n －1a n ＋1－1的前n 项和为________． 解析：因为a 5－a 1＝30，a 4－a 2＝12， 所以a 1(q 4－1)＝30，a 1(q 3－q )＝12， 两式相除，化简得2q 2－5q ＋2＝0， 解得q ＝12或2，因为q ＞1，所以q ＝2，a 1＝2. 所以a n ＝2·2n －1＝2n.所以a na n －1a n ＋1－1＝2n2n－12n ＋1－1＝12n－1－12n ＋1－1， 所以T n ＝1－13＋13－17＋…＋12n －1－12n ＋1－1＝1－12n ＋1－1.答案：1－12n ＋1－16．若数列{a n }满足a n －(－1)na n －1＝n (n ≥2)，S n 是{a n }的前n 项和，则S 40＝________. 解析：当n ＝2k 时，即a 2k －a 2k －1＝2k ， ① 当n ＝2k －1时，即a 2k －1＋a 2k －2＝2k －1，② 当n ＝2k ＋1时，即a 2k ＋1＋a 2k ＝2k ＋1， ③ ①＋②得a 2k ＋a 2k －2＝4k －1， ③－①得a 2k ＋1＋a 2k －1＝1，S 40＝(a 1＋a 3＋a 5＋...＋a 39)＋(a 2＋a 4＋a 6＋a 8＋...＋a 40)＝1×10＋(7＋15＋23＋ (79)＝10＋107＋792＝440. 答案：440二保高考，全练题型做到高考达标1．在数列{a n }中，若a 1＝2，且对任意正整数m ，k ，总有a m ＋k ＝a m ＋a k ，则{a n }的前n 项和S n ＝________.解析：依题意得a n ＋1＝a n ＋a 1，即有a n ＋1－a n ＝a 1＝2，所以数列{a n }是以2为首项、2为公差的等差数列，a n ＝2＋2(n －1)＝2n ，S n ＝n 2＋2n2＝n 2＋n .答案：n 2＋n2．已知数列{a n }中，a n ＝－4n ＋5，等比数列{b n }的公比q 满足q ＝a n －a n －1(n ≥2)且b 1＝a 2，则|b 1|＋|b 2|＋|b 3|＋…＋|b n |＝________.解析：由已知得b 1＝a 2＝－3，q ＝－4， 所以b n ＝(－3)×(－4)n －1，所以|b n |＝3×4n －1，即{|b n |}是以3为首项，4为公比的等比数列． 所以|b 1|＋|b 2|＋…＋|b n |＝31－4n1－4＝4n－1.答案：4n－13．已知数列5,6,1，－5，…，该数列的特点是从第二项起，每一项都等于它的前后两项之和，则这个数列的前16项之和S 16＝________.解析：根据题意这个数列的前7项分别为5,6,1，－5，－6，－1,5,6，发现从第7项起，数列重复出现，所以此数列为周期数列，且周期为6，前6项和为5＋6＋1＋(－5)＋(－6)＋(－1)＝0.又因为16＝2×6＋4，所以这个数列的前16项之和S 16＝2×0＋7＝7. 答案：74．对于数列{a n }，定义数列{a n ＋1－a n }为数列{a n }的“差数列”，若a 1＝2，数列{a n }的“差数列”的通项为2n，则数列{a n }的前n 项和S n ＝________.解析：因为a n ＋1－a n ＝2n，所以a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝2n －1＋2n －2＋…＋22＋2＋2＝2－2n 1－2＋2＝2n －2＋2＝2n ，所以S n ＝2－2n ＋11－2＝2n ＋1－2.答案：2n ＋1－25．(2019·宿迁调研)已知数列{}a n 中，a 1＝1，a 2＝3，若a n ＋2＋2a n ＋1＋a n ＝0对任意n ∈N *都成立，则数列{}a n 的前n 项和S n ＝________.解析：∵a 1＝1，a 2＝3，a n ＋2＋2a n ＋1＋a n ＝0， ∴a n ＋2＋a n ＋1＝－(a n ＋1＋a n )，a 2＋a 1＝4.则数列{}a n ＋1＋a n 是首项为4，公比为－1的等比数列， ∴a n ＋1＋a n ＝4×(－1)n －1.当n ＝2k －1时，a 2k ＋a 2k －1＝4×(－1)2k －2＝4.∴S n ＝(a 1＋a 2)＋(a 3＋a 4)＋…＋(a 2k －1＋a 2k )＝4k ＝2n . 当n ＝2k 时，a 2k ＋1＋a 2k ＝－4.S n ＝a 1＋(a 2＋a 3)＋…＋(a 2k －2＋a 2k －1)＝1－4×(k －1)＝5－4k ＝5－4×n ＋12＝3－2n .∴S n ＝⎩⎪⎨⎪⎧3－2n ，n 为奇数，2n ，n 为偶数.答案：⎩⎪⎨⎪⎧3－2n ，n 为奇数，2n ，n 为偶数6．在等差数列{a n }中，首项a 1＝3，公差d ＝2，若某学生对其中连续10项进行求和，在漏掉一项的前提下，求得余下9项的和为185，则此连续10项的和为________．解析：由已知条件可得数列{a n }的通项公式a n ＝2n ＋1，设连续10项为a i ＋1，a i ＋2，a i ＋3，…，a i ＋10，i ∈N ，设漏掉的一项为a i ＋k,1≤k ≤10，由a i ＋1＋a i ＋10×102－a i ＋k ＝185，得(2i ＋3＋2i ＋21)×5－2i －2k －1＝185，即18i －2k ＝66，即9i －k ＝33，所以34≤9i ＝k ＋33≤43,3＜349≤i ≤439＜5，所以i ＝4，此时，由36＝33＋k 得k ＝3，所以a i ＋k ＝a 7＝15，故此连续10项的和为200.答案：2007．(2019·邵阳模拟)《九章算术》是我国古代的数学名著，书中《均属章》有如下问题：“今有五人分五钱，令上二人所得与下三人等．问各得几何．”其意思为“已知A ，B ，C ，D ，E 五人分5钱，A ，B 两人所得与C ，D ，E 三人所得相同，且A ，B ，C ，D ，E 每人所得依次成等差数列．问五人各得多少钱？”(“钱”是古代的一种重量单位)．在这个问题中，E 分得________钱．解析：由题意，设A 所得为a －4d ，B 所得为a －3d ，C 所得为a －2d ，D 所得为a －d ，E 所得为a ，则⎩⎪⎨⎪⎧5a －10d ＝5，2a －7d ＝3a －3d ，解得a ＝23，故E 分得23钱．答案：238．已知数列{a n }中，a 1＝2，a 2n ＝a n ＋1，a 2n ＋1＝n －a n ，则{a n }的前100项和为________． 解析：由a 1＝2，a 2n ＝a n ＋1，a 2n ＋1＝n －a n ，得a 2n ＋a 2n ＋1＝n ＋1，所以a 1＋(a 2＋a 3)＋(a 4＋a 5)＋…＋(a 98＋a 99)＝2＋2＋3＋…＋50＝1 276，因为a 100＝1＋a 50＝1＋(1＋a 25)＝2＋(12－a 12)＝14－(1＋a 6)＝13－(1＋a 3)＝12－(1－a 1)＝13，所以a 1＋a 2＋…＋a 100＝1 276＋13＝1 289.答案：1 2899．(2018·苏北四市期末)已知正项数列{a n }的前n 项和为S n ，且a 1＝a ，(a n ＋1)(a n ＋1＋1)＝6(S n ＋n )，n ∈N *.(1)求数列{a n }的通项公式；(2)若对于∀n ∈N *，都有S n ≤n (3n ＋1)成立，求实数a 的取值范围． 解：(1)当n ＝1时，(a 1＋1)(a 2＋1)＝6(S 1＋1)，故a 2＝5. 当n ≥2时，(a n －1＋1)(a n ＋1)＝6(S n －1＋n －1)，所以(a n ＋1)(a n ＋1＋1)－(a n －1＋1)(a n ＋1)＝6(S n ＋n )－6(S n －1＋n －1)， 即(a n ＋1)(a n ＋1－a n －1)＝6(a n ＋1)． 又a n ＞0，所以a n ＋1－a n －1＝6，所以a 2k －1＝a ＋6(k －1)＝6k ＋a －6，a 2k ＝5＋6(k －1)＝6k －1，故a n ＝⎩⎪⎨⎪⎧3n ＋a －3，n 为奇数，3n －1，n 为偶数.(2)当n 为奇数时，S n ＝12(3n ＋a －2)(n ＋1)－n ，由S n ≤n (3n ＋1)，得a ≤3n 2＋3n ＋2n ＋1恒成立，令f (n )＝3n 2＋3n ＋2n ＋1，则f (n ＋1)－f (n )＝3n 2＋9n ＋4n ＋2n ＋1＞0，所以a ≤f (1)＝4.当n 为偶数时，S n ＝12n (3n ＋a ＋1)－n ，由S n ≤n (3n ＋1)得，a ≤3(n ＋1)恒成立， 所以a ≤9.又a 1＝a ＞0，所以实数a 的取值范围是(0,4]．10．(2019·宿迁中学调研)已知各项均为正数的数列{a n }的首项a 1＝1，S n 是数列{a n }的前n 项和，且满足a n S n ＋1－a n ＋1S n ＋a n －a n ＋1＝λa n a n ＋1(λ≠0，n ∈N *)．(1)若a 1，a 2，a 3成等比数列，求实数λ的值； (2)若λ＝12，求S n .解：(1)令n ＝1，得a 2＝21＋λ.令n ＝2，得a 2S 3－a 3S 2＋a 2－a 3＝λa 2a 3， 所以a 3＝2λ＋4λ＋12λ＋1.由a 22＝a 1a 3，得⎝⎛⎭⎪⎫21＋λ2＝2λ＋4λ＋12λ＋1， 因为λ≠0，所以λ＝1.(2)当λ＝12时，a n S n ＋1－a n ＋1S n ＋a n －a n ＋1＝12a n a n ＋1，所以S n ＋1a n ＋1－S n a n ＋1a n ＋1－1a n ＝12，即S n ＋1＋1a n ＋1－S n ＋1a n ＝12， 所以数列⎩⎨⎧⎭⎬⎫S n ＋1a n 是以2为首项，12为公差的等差数列，所以S n ＋1a n ＝2＋(n －1)·12， 即S n ＋1＝⎝ ⎛⎭⎪⎫n 2＋32a n ，①当n ≥2时，S n －1＋1＝⎝ ⎛⎭⎪⎫n2＋1a n －1，② ①－②得，a n ＝n ＋32a n －n ＋22a n －1，即(n ＋1)a n ＝(n ＋2)a n －1，所以a n n ＋2＝a n －1n ＋1(n ≥2)， 所以⎩⎨⎧⎭⎬⎫a n n ＋2是常数列，且为13，所以a n ＝13(n ＋2). 代入①得S n ＝⎝ ⎛⎭⎪⎫n 2＋32a n －1＝n 2＋5n 6. 三上台阶，自主选做志在冲刺名校1．(2018·启东检测)《九章算术》中的“两鼠穿墙题”是我国数学的古典名题：“今有垣厚若干尺，两鼠对穿，大鼠日一尺，小鼠也日一尺，大鼠日自倍，小鼠日自半，问何日相逢，各穿几何？”题意是“有两只老鼠从墙的两边打洞穿墙，大老鼠第一天进一尺，以后每天加倍；小老鼠第一天也进一尺，以后每天减半．”如果墙足够厚，S n 为前n 天两只老鼠打洞长度之和，则S n ＝________尺．解析：依题意大老鼠每天打洞的距离构成以1为首项，2为公比的等比数列，所以前n 天大老鼠打洞的距离共为1×1－2n1－2＝2n－1.同理可得前n 天小老鼠打洞的距离共为1×⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫12n 1－12＝2－12n －1，所以S n ＝2n －1＋2－12n －1＝2n－12n －1＋1. 答案：2n－12n －1＋12．(2018·苏州高三暑假测试)等差数列{a n }的前n 项和为S n ，且a n －S n ＝n 2－16n ＋15(n ∈N *)，若对任意n ∈N *，总有S n ≤S k ，则k 的值为________．解析：设等差数列{a n }的公差为d ，则a n －S n ＝a 1＋(n －1)d －⎣⎢⎡⎦⎥⎤na 1＋n n －12d ＝－d 2n 2＋⎝ ⎛⎭⎪⎫32d －a 1n ＋a 1－d ＝n 2－16n ＋15，所以⎩⎪⎨⎪⎧－d2＝1，32d －a 1＝－16，a 1－d ＝15，解得⎩⎪⎨⎪⎧a 1＝13，d ＝－2，所以S n ＝13n ＋n n －12×(－2)＝－n 2＋14n ＝－(n －7)2＋49，所以(S n )max ＝S 7，所以S n ≤S 7对任意n ∈N *恒成立，所以k 的值为7.答案：73．(2019·南京一模)平面内的“向量列”{a n }，如果对于任意的正整数n ，均有a n ＋1－a n ＝d ，则称此“向量列”为“等差向量列”，d 称为“公差向量”；平面内的“向量列”{b n }，如果对于任意的正整数n ，均有b n ＋1＝q ·b n (q ≠0)，则称此“向量列”为“等比向量列”，常数q 称为“公比”．(1)如果“向量列”{a n }是“等差向量列”，用a 1和“公差向量”d 表示a 1＋a 2＋…＋a n ； (2)已知{a n }是“等差向量列”，“公差向量”d ＝(3,0)，a 1＝(1,1)，a n ＝(x n ，y n )，{b n }是“等比向量列”，“公比”q ＝2，b 1＝(1,3)，b n ＝(m n ，k n )，求a 1·b 1＋a 2·b 2＋…＋a n ·b n .解：(1)∵“向量列”{a n }是“等差向量列”， ∴a 1＋a 2…＋a n ＝n a 1＋(1＋2＋…＋n －1)d ＝n a 1＋n n －12d.(2)∵a 1＝(1,1)，d ＝(3,0)，∴a n ＝(3n －2,1)． ∵b 1＝(1,3)，q ＝2，∴b n ＝(2n －1,3·2n －1)．∴a n ·b n ＝(3n －2,1)·(2n －1,3·2n －1)＝(3n －2)·2n －1＋3·2n －1＝(3n ＋1)·2n －1，设S n ＝a 1·b 1＋a 2·b 2＋…＋a n ·b n ， 则S n ＝＝4·20＋7·21＋…＋(3n ＋1)·2n －1，2S n ＝4·2＋7·22＋…＋(3n ＋1)·2n， 两式相减可得，－S n ＝4＋3(2＋22＋…＋2n －1)－(3n ＋1)·2n＝4＋3·21－2n －11－2－(3n ＋1)·2n ＝(2－3n )·2n－2，∴a 1·b 1＋a 2·b 2＋…＋a n ·b n ＝(3n －2)·2n＋2.。

2019-2020年高考数学一轮总复习第五章数列5.3等比数列及其前n 项和课时跟踪检测理[课 时 跟 踪 检 测][基 础 达 标]1．已知数列{a n }为等比数列，若a 4＋a 6＝10，则a 7(a 1＋2a 3)＋a 3a 9的值为( ) A ．10 B ．20 C ．100D ．200解析：a 7(a 1＋2a 3)＋a 3a 9＝a 7a 1＋2a 7a 3＋a 3a 9＝a 24＋2a 4a 6＋a 26＝(a 4＋a 6)2＝102＝100. 答案：C2．设等比数列{a n }中，前n 项和为S n ，已知S 3＝8，S 6＝7，则a 7＋a 8＋a 9等于( ) A.18 B ．－18C.578D ．558解析：因为a 7＋a 8＋a 9＝S 9－S 6，且S 3，S 6－S 3，S 9－S 6也成等比数列，即8，－1，S 9－S 6成等比数列，所以8(S 9－S 6)＝1，即S 9－S 6＝18.所以a 7＋a 8＋a 9＝18.答案：A3．已知数列{a n }满足log 3a n ＋1＝log 3a n ＋1(n ∈N *)，且a 2＋a 4＋a 6＝9，则log 13(a 5＋a 7＋a 9)的值是( )A ．－5B ．－15C ．5D ．15解析：∵log 3a n ＋1＝log 3a n ＋1，∴a n ＋1＝3a n . ∴数列{a n }是公比q ＝3的等比数列． ∵a 5＋a 7＋a 9＝q 3(a 2＋a 4＋a 6)，∴log 13(a 5＋a 7＋a 9)＝log 13(9×33)＝log 1335＝－5.答案：A4．(xx 届太原一模)在单调递减的等比数列{a n }中，若a 3＝1，a 2＋a 4＝52，则a 1＝( )A ．2B ．4 C. 2D ．2 2解析：在等比数列{a n }中，a 2a 4＝a 23＝1，又a 2＋a 4＝52，数列{a n }为递减数列，所以a 2＝2，a 4＝12，所以q 2＝a 4a 2＝14，所以q ＝12，a 1＝a 2q＝4.答案：B5．(xx 届莱芜模拟)已知数列{a n }，{b n }满足a 1＝b 1＝3，a n ＋1－a n ＝b n ＋1b n＝3，n ∈N *，若数列{c n }满足c n ＝ba n ，则c 2 017＝( )A ．92 016B ．272 016C ．92 017D ．272 017解析：由已知条件知{a n }是首项为3，公差为3的等差数列，数列{b n }是首项为3，公比为3的等比数列，所以a n ＝3n ，b n ＝3n. 又c n ＝ba n ＝33n， 所以c 2 017＝33×2 017＝272 017.答案：D6．(xx 届海口市调研测试)设S n 为等比数列{a n }的前n 项和，a 2－8a 5＝0，则S 8S 4的值为( )A.12 B ．1716 C ．2D ．17解析：设{a n }的公比为q ，依题意得a 5a 2＝18＝q 3，因此q ＝12.注意到a 5＋a 6＋a 7＋a 8＝q 4(a 1＋a 2＋a 3＋a 4)，即有S 8－S 4＝q 4S 4，因此S 8＝(q 4＋1)S 4，S 8S 4＝q 4＋1＝1716，选B.答案：B7．(xx 届衡阳模拟)在等比数列{a n }中，a 1＝2，前n 项和为S n ，若数列{a n ＋1}也是等比数列，则S n ＝( )A ．2n ＋1－2 B ．3n C ．2nD ．3n－1解析：因为数列{a n }为等比数列，a 1＝2，设其公比为q ，则a n ＝2qn －1，因为数列{a n ＋1}也是等比数列，所以(a n ＋1＋1)2＝(a n ＋1)(a n ＋2＋1)⇒a 2n ＋1＋2a n ＋1＝a n a n ＋2＋a n ＋a n ＋2⇒a n ＋a n＋2＝2a n ＋1⇒a n (1＋q 2－2q )＝0⇒q ＝1，即a n ＝2，所以S n ＝2n ，故选C.答案：C8．(xx 届广州市五校联考)已知数列{a n }的首项a 1＝2，数列{b n }为等比数列，且b n ＝a n ＋1a n，若b 10b 11＝2，则a 21＝( )A ．29B ．210C ．211D ．212解析：由b n ＝a n ＋1a n ，且a 1＝2，得b 1＝a 2a 1＝a 22，a 2＝2b 1；b 2＝a 3a 2，a 3＝a 2b 2＝2b 1b 2；b 3＝a 4a 3，a 4＝a 3b 3＝2b 1b 2b 3；…；a n ＝2b 1b 2b 3…b n －1，所以a 21＝2b 1b 2b 3…b 20，又{b n }为等比数列，所以a 21＝2(b 1b 20)(b 2b 19)…(b 10b 11)＝2(b 10b 11)10＝211. 答案：C9．由正数组成的等比数列{a n }满足a 3a 8＝32，则log 2a 1＋log 2a 2＋…＋log 2a 10＝________. 解析：log 2a 1＋log 2a 2＋…＋log 2a 10＝log 2(a 1a 10)·(a 2a 9)·…·(a 5a 6)＝log 2(a 3a 8)5＝log 2225＝25.答案：2510．设S n 为等比数列{a n }的前n 项和．若a 1＝1，且3S 1,2S 2，S 3成等差数列，则a n ＝________. 解析：因为3S 1,2S 2，S 3成等差数列，所以4S 2＝3S 1＋S 3，即4(a 1＋a 2)＝3a 1＋a 1＋a 2＋a 3.化简得a 3a 2＝3，即等比数列{a n }的公比q ＝3，故a n ＝1×3n －1＝3n －1.答案：3n －111．(xx 届南昌模拟)已知公比不为1的等比数列{a n }的首项a 1＝12，前n 项和为S n ，且a 4＋S 4，a 5＋S 5，a 6＋S 6成等差数列．(1)求等比数列{a n }的通项公式；(2)对n ∈N *，在a n 与a n ＋1之间插入3n 个数，使这3n＋2个数成等差数列，记插入的这3n个数的和为b n ，求数列{b n }的前n 项和T n .解：(1)因为a 4＋S 4，a 5＋S 5，a 6＋S 6成等差数列， 所以a 5＋S 5－a 4－S 4＝a 6＋S 6－a 5－S 5， 即2a 6－3a 5＋a 4＝0， 所以2q 2－3q ＋1＝0， 因为q ≠1， 所以q ＝12，所以等比数列{a n }的通项公式为a n ＝12n .(2)b n ＝a n ＋a n ＋12·3n＝34⎝ ⎛⎭⎪⎫32n ，T n ＝34×32－⎝ ⎛⎭⎪⎫32n ＋11－32＝94⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫32n －1.12．设数列{a n }的前n 项和为S n (n ∈N *)．已知a 1＝1，a 2＝32，a 3＝54，且当n ≥2时，4S n＋2＋5S n ＝8S n ＋1＋S n －1. (1)求a 4的值；(2)证明：⎩⎨⎧⎭⎬⎫a n ＋1－12a n 为等比数列．解：(1)当n ＝2时，4S 4＋5S 2＝8S 3＋S 1，即4⎝ ⎛⎭⎪⎫1＋32＋54＋a 4＋5⎝ ⎛⎭⎪⎫1＋32＝81＋32＋54＋1，解得a 4＝78.(2)证明：由4S n ＋2＋5S n ＝8S n ＋1＋S n －1(n ≥2)， 得4S n ＋2－4S n ＋1＋S n －S n －1＝4S n ＋1－4S n (n ≥2)， 即4a n ＋2＋a n ＝4a n ＋1(n ≥2)．∵4a 3＋a 1＝4×54＋1＝6＝4a 2符合上式，∴4a n ＋2＋a n ＝4a n ＋1(n ≥1)， ∴a n ＋2－12a n ＋1a n ＋1－12a n＝4a n ＋2－2a n ＋14a n ＋1－2a n＝4a n ＋1－a n －2a n ＋14a n ＋1－2a n ＝2a n ＋1－a n 22a n ＋1－a n ＝12，∴数列⎩⎨⎧⎭⎬⎫a n ＋1－12a n 是以a 2－12a 1＝1为首项，12为公比的等比数列．[能 力 提 升]1．若{a n }是正项递增等比数列，T n 表示其前n 项之积，且T 10＝T 20，则当T n 取最小值时，n 的值为________．解析：T 10＝T 20⇒a 11…a 20＝1⇒(a 15a 16)5＝1⇒a 15a 16＝1，又{a n }是正项递增等比数列，所以0<a 1<a 2<…<a 14<a 15<1<a 16<a 17<…，因此当T n 取最小值时，n 的值为15.答案：152．(xx 届山西吕梁质检)已知数列2,8,4，12，…，该数列的特点是从第2项起，每一项都等于它的前后两项之积，则这个数列的前2 018项之积T 2 018等于________．解析：数列2,8,4，12，…，该数列的特点是从第2项起，每一项都等于它的前后两项之积，这个数列的前8项分别为2,8,4，12，18，14，2,8，易得从第7项起，数字重复出现，所以此数列为周期数列，且周期为6，前6项积为2×8×4×12×18×14＝1.又因为2 018＝336×6＋2，所以这个数列的前2 018项之积T 2 018＝1336×2×8＝16. 答案：163．已知数列{a n }满足a 1＝5，a 2＝5，a n ＋1＝a n ＋6a n －1(n ≥2)． (1)求证：{a n ＋1＋2a n }是等比数列； (2)求数列{a n }的通项公式．解：(1)证明：∵a n ＋1＝a n ＋6a n －1(n ≥2)， ∴a n ＋1＋2a n ＝3a n ＋6a n －1＝3(a n ＋2a n －1)(n ≥2)． ∵a 1＝5，a 2＝5，∴a 2＋2a 1＝15， ∴a n ＋2a n －1≠0(n ≥2)，∴a n ＋1＋2a na n ＋2a n －1＝3(n ≥2)，∴数列{a n ＋1＋2a n }是以15为首项，3为公比的等比数列． (2)由(1)得a n ＋1＋2a n ＝15×3n －1＝5×3n，则a n ＋1＝－2a n ＋5×3n， ∴a n ＋1－3n ＋1＝－2(a n －3n)．又∵a 1－3＝2，∴a n －3n≠0，∴{a n －3n}是以2为首项，－2为公比的等比数列． ∴a n －3n＝2×(－2)n －1，即a n ＝2×(－2)n －1＋3n.2019-2020年高考数学一轮总复习第五章数列5.4数列求和课时跟踪检测理[课 时 跟 踪 检 测][基 础 达 标]1．已知数列{a n }是等差数列，a 1＝tan225°，a 5＝13a 1，设S n 为数列{(－1)na n }的前n 项和，则S 2 014＝( )A ．2 015B ．－2 015C ．3 021D ．－3 022解析：由题知a 1＝tan(180°＋45°)＝1，∴a 5＝13 ∴d ＝a 5－a 15－1＝124＝3. ∴a n ＝1＋3(n －1)＝3n －2. 设b n ＝(－1)na n ＝(－1)n(3n －2)，∴S 2 014＝(－1＋4)＋(－7＋10)＋…＋(－6 037＋6 040)＝3×1 007＝3 021.故选C. 答案：C2．设{a n }是公差不为零的等差数列，a 2＝2，且a 1，a 3，a 9成等比数列，则数列{a n }的前n 项和S n ＝( )A.n 24＋7n 4 B ．n 22＋3n 2C.n 24＋3n4D ．n 22＋n2解析：设等差数列{a n }的公差为d ，则 由a 23＝a 1a 9得(a 2＋d )2＝(a 2－d )(a 2＋7d )， 代入a 2＝2，解得d ＝1或d ＝0(舍)． ∴a n ＝2＋(n －2)×1＝n ， ∴S n ＝a 1＋a n n2＝1＋n n 2＝n 22＋n 2.故选D. 答案：D3．等比数列{a n }的前n 项和为S n ，已知a 2a 3＝2a 1，且a 4与2a 7的等差中项为54，则S 5＝( )A ．29B ．31C ．33D ．36解析：设等比数列{a n }的公比为q 则a 21q 3＝2a 1，①a 1q 3＋2a 1q 6＝52，②解得a 1＝16，q ＝12，∴S 5＝a 11－q 51－q＝31，故选B.答案：B4．已知等比数列{a n }的各项均为正数，a 1＝1，公比为q ；等差数列{b n }中，b 1＝3，且{b n }的前n 项和为S n ，a 3＋S 3＝27，q ＝S 2a 2.(1)求{a n }与{b n }的通项公式；(2)设数列{c n }满足c n ＝32S n ，求{c n }的前n 项和T n .解：(1)设数列{b n }的公差为d ， ∵a 3＋S 3＝27，q ＝S 2a 2，∴⎩⎪⎨⎪⎧q 2＋3d ＝18，6＋d ＝q 2.求得q ＝3，d ＝3，∴a n ＝3n －1，b n ＝3n .(2)由题意得S n ＝n 3＋3n2，c n ＝32S n ＝32×23×1n n ＋1＝1n －1n ＋1. ∴T n ＝1－12＋12－13＋13－14＋…＋1n －1n ＋1＝1－1n ＋1＝nn ＋1.5．(xx 届广州综合测试)已知数列{a n }是等比数列，a 2＝4，a 3＋2是a 2和a 4的等差中项． (1)求数列{a n }的通项公式；(2)设b n ＝2log 2a n －1，求数列{a n b n }的前n 项和T n . 解：(1)设数列{a n }的公比为q ， 因为a 2＝4，所以a 3＝4q ，a 4＝4q 2. 因为a 3＋2是a 2和a 4的等差中项， 所以2(a 3＋2)＝a 2＋a 4， 化简得q 2－2q ＝0. 因为公比q ≠0，所以q ＝2. 所以a n ＝a 2qn －2＝4×2n －2＝2n (n ∈N *)．(2)因为a n ＝2n，所以b n ＝2log 2a n －1＝2n －1， 所以a n b n ＝(2n －1)2n，则T n ＝1×2＋3×22＋5×23＋…＋(2n －3)2n －1＋(2n －1)2n，①2T n ＝1×22＋3×23＋5×24＋…＋(2n －3)2n＋(2n －1)·2n ＋1.②由①－②得，－T n ＝2＋2×22＋2×23＋…＋2×2n －(2n －1)2n ＋1＝2＋2×41－2n －11－2－(2n －1)2n ＋1＝－6－(2n －3)2n ＋1，所以T n ＝6＋(2n －3)2n ＋1.6．S n 为数列{a n }的前n 项和，已知a n >0，a 2n ＋2a n ＝4S n ＋3. (1)求{a n }的通项公式； (2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和．解：(1)由a 2n ＋2a n ＝4S n ＋3，① 可知a 2n ＋1＋2a n ＋1＝4S n ＋1＋3.②②－①，得a 2n ＋1－a 2n ＋2(a n ＋1－a n )＝4a n ＋1， 即2(a n ＋1＋a n )＝a 2n ＋1－a 2n ＝(a n ＋1＋a n )(a n ＋1－a n )． 由a n >0，得a n ＋1－a n ＝2.又a 21＋2a 1＝4a 1＋3，解得a 1＝－1(舍去)或a 1＝3. 所以{a n }是首项为3，公差为2的等差数列， 通项公式为a n ＝2n ＋1. (2)由a n ＝2n ＋1可知b n ＝1a n a n ＋1＝12n ＋12n ＋3＝12⎝ ⎛⎭⎪⎫12n ＋1－12n ＋3.设数列{b n }的前n 项和为T n ，则T n ＝b 1＋b 2＋…＋b n＝12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫13－15＋⎝ ⎛⎭⎪⎫15－17＋…＋⎝ ⎛⎭⎪⎫12n ＋1－12n ＋3＝n32n ＋3.7．已知数列{a n }与{b n }满足a n ＋1－a n ＝2(b n ＋1－b n )(n ∈N *)． (1)若a 1＝1，b n ＝3n ＋5，求数列{a n }的通项公式；(2)若a 1＝6，b n ＝2n(n ∈N *)且λa n >2n ＋n ＋2λ对一切n ∈N *恒成立， 求实数λ的取值范围．解：(1)因为a n ＋1－a n ＝2(b n ＋1－b n )，b n ＝3n ＋5， 所以a n ＋1－a n ＝2(b n ＋1－b n )＝2(3n ＋8－3n －5)＝6， 所以{a n }是等差数列，首项为1，公差为6， 即a n ＝6n －5. (2)因为b n ＝2n， 所以a n ＋1－a n ＝2(2n ＋1－2n )＝2n ＋1，当n ≥2时，a n ＝(a n －a n －1)＋(a n －1－a n －2)＋…＋(a 2－a 1)＋a 1＝2n ＋2n －1＋…＋22＋6＝2n ＋1＋2，当n ＝1时，a 1＝6，符合上式，所以a n ＝2n ＋1＋2，由λa n >2n＋n ＋2λ得λ>2n＋n 2n ＋1＝12＋n 2n ＋1，令f (n )＝12＋n 2n ＋1，因为f (n ＋1)－f (n )＝n ＋12n ＋2－n 2n ＋1＝1－n 2n ＋2≤0， 所以12＋n2n ＋1在n ≥1时单调递减，所以当n ＝1,2时，2n＋n 2n ＋1取最大值34，故λ的取值范围为⎝ ⎛⎭⎪⎫34，＋∞. [能 力 提 升]1．已知数列{a n }的首项为a 1＝1，前n 项和为S n ，且数列⎩⎨⎧⎭⎬⎫S n n 是公差为2的等差数列．(1)求数列{a n }的通项公式；(2)若b n ＝(－1)na n ，求数列{b n }的前n 项和T n . 解：(1)由已知得S n n＝1＋(n －1)×2＝2n －1， 所以S n ＝2n 2－n ， 当n ≥2时，a n ＝S n －S n －1＝2n 2－n －[2(n －1)2－(n －1)]＝4n －3. a 1＝1＝4×1－3，所以a n ＝4n －3，n ∈N *.(2)由(1)可得b n ＝(－1)na n ＝(－1)n(4n －3)． 当n 为偶数时，T n ＝(－1＋5)＋(－9＋13)＋…＋[－(4n －7)＋(4n －3)]＝4×n2＝2n ，当n 为奇数时，n ＋1为偶数，T n ＝T n ＋1－b n ＋1＝2(n ＋1)－(4n ＋1)＝－2n ＋1，综上，T n ＝⎩⎪⎨⎪⎧2n ，n ＝2k ，k ∈N *，－2n ＋1，n ＝2k －1，k ∈N *.2．在数列{a n }中，已知a n >1，a 1＝1＋3，且a n ＋1－a n ＝2a n ＋1＋a n －2，记b n ＝(a n －1)2，n ∈N *.(1)求数列{b n }的通项公式；(2)设数列{b n }的前n 项和为S n ，证明：13≤1S 1＋1S 2＋1S 3＋…＋1S n <34.解：(1)因为a n ＋1－a n ＝2a n ＋1＋a n －2，所以a 2n ＋1－a 2n －2a n ＋1＋2a n ＝2， 即(a n ＋1－1)2－(a n －1)2＝2. 又b n ＝(a n －1)2，n ∈N *，所以b n ＋1－b n ＝2，数列{b n }是以b 1＝(1＋3－1)2＝3为首项，2为公差的等差数列， 故b n ＝2n ＋1，n ∈N *. (2)证明：由(1)得S n ＝n 3＋2n ＋12＝n (n ＋2)，所以1S n ＝1nn ＋2＝12⎝ ⎛⎭⎪⎫1n －1n ＋2，n ∈N *， 所以1S 1＋1S 2＋1S 3＋…＋1S n＝12⎝ ⎛⎭⎪⎫1－13＋12－14＋13－15＋…＋1n －1n ＋2＝12⎝ ⎛⎭⎪⎫32－1n ＋1－1n ＋2＝34－12⎝ ⎛⎭⎪⎫1n ＋1＋1n ＋2<34.记T n ＝1S 1＋1S 2＋1S 3＋…＋1S n，因为1S n>0，n ∈N *，所以T n 单调递增．故T n ≥T 1＝1S 1＝13.综上13≤1S 1＋1S 2＋…＋1S n <34.3．已知各项均为正数的数列{a n }的前n 项和为S n ，且满足a 2n ＋a n ＝2S n . (1)求数列{a n }的通项公式； (2)求证：S n2<S 1＋S 2＋…＋S n <S n ＋1－12.解：(1)因为当n ∈N *时，a 2n ＋a n ＝2S n ， 故当n >1时，a 2n －1＋a n －1＝2S n －1，两式相减得，a 2n －a 2n －1＋a n －a n －1＝2S n －2S n －1＝2a n ， 即(a n ＋a n －1)(a n －a n －1)＝a n ＋a n －1.因为a n >0，所以a n ＋a n －1>0，所以当n >1时，a n －a n －1＝1.又当n ＝1时，a 21＋a 1＝2S 1＝2a 1，得a 1＝1， 所以数列{a n }是以1为首项，1为公差的等差数列， 所以a n ＝n .(2)证明：由(1)及等差数列的前n 项和公式知S n ＝n n ＋12，所以S n ＝ n n ＋12>n 22＝n2， 所以S 1＋S 2＋…＋S n >12＋22＋…＋n 2＝ 1＋2＋…＋n 2＝S n 2. 又S n ＝ n n ＋12<n ＋122＝n ＋12， 所以S 1＋S 2＋…＋S n <22＋32＋…＋n ＋12＝1＋2＋…＋n ＋12－12＝S n ＋1－12， 所以S n2<S 1＋S 2＋…＋S n <S n ＋1－12.。

考点测试34　一元二次不等式及其解法高考概览高考在本考点的常考题型为选择题、填空题，分值5分，中、低等难度考纲研读1．会从实际问题的情境中抽象出一元二次不等式模型2．通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系3．会解一元二次不等式一、基础小题1．不等式2x 2－x －3＞0的解集是( )A ．－，132B ．(－∞，－1)∪，＋∞32C ．－1，32D ．－∞，－∪(1，＋∞)32答案　B解析　2x 2－x －3＞0可因式分解为(x ＋1)(2x －3)＞0，解得x ＞或x ＜－1，∴32不等式2x 2－x －3＞0的解集是(－∞，－1)∪，＋∞．故选B ．322．若不等式ax 2＋bx －2<0的解集为，则ab ＝( ){x －2<x <14}A ．－28B ．－26C ．28D ．26答案　C解析　∵－2，是方程ax 2＋bx －2＝0的两根，14∴Error!∴Error!∴ab ＝28．3．不等式x 2＋ax ＋4<0的解集不是空集，则实数a 的取值范围是( )A ．[－4，4]B ．(－4，4)C ．(－∞，－4]∪[4，＋∞)D ．(－∞，－4)∪(4，＋∞)答案　D解析　不等式x 2＋ax ＋4<0的解集不是空集，只需Δ＝a 2－16>0，∴a <－4或a >4．故选D ．4．关于x 的不等式x 2－2ax －8a 2<0(a >0)的解集为(x 1，x 2)，且x 2－x 1＝15，则a ＝( )A ．B ．C ．D ．5272154152答案　A解析　由x 2－2ax －8a 2＝0的两个根为x 1＝－2a ，x 2＝4a ，得6a ＝15，所以a ＝．525．若函数f (x )＝的定义域为R ，则实数k 的取值范围是( )kx 2－6kx ＋k ＋8A ．{k |0＜k ≤1} B ．{k |k ＜0或k ＞1}C ．{k |0≤k ≤1}D ．{k |k ＞1}答案　C解析　当k ＝0时，8＞0恒成立；当k ≠0时，只需Error!即Error!则0＜k ≤1．综上，0≤k ≤1．6．不等式|x 2－x |<2的解集为( )A ．(－1，2)B ．(－1，1)C ．(－2，1)D ．(－2，2)答案　A解析　由|x 2－x |<2，得－2<x 2－x <2，即Error!由①，得－1<x <2．由②，得x ∈R ．所以解集为(－1，2)．故选A ．7．某商场若将进货单价为8元的商品按每件10元出售，每天可销售100件，现准备采用提高售价来增加利润．已知这种商品每件销售价提高1元，销售量就要减少10件．那么要保证每天所赚的利润在320元以上，销售价每件应定为( )A ．12元B ．16元C ．12元到16元之间D ．10元到14元之间答案　C解析　设销售价定为每件x 元，利润为y ，则y ＝(x －8)[100－10(x －10)]，依题意有(x －8)[100－10(x －10)]>320，即x 2－28x ＋192<0，解得12<x <16，所以每件销售价应定为12元到16元之间．8．如果二次函数y ＝3x 2＋2(a －1)x ＋b 在区间(－∞，1]上是减函数，那么a 的取值范围是( )A ．(－∞，－2)B ．(2，＋∞)C ．(－∞，－2]D ．[2，＋∞)答案　C解析　∵二次函数y ＝3x 2＋2(a －1)x ＋b 在区间(－∞，1]上是减函数，∴－≥1，解得a ≤－2．故选C ．2(a －1)2×39．设函数f (x )＝Error!若f (－4)＝f (0)，f (－2)＝0，则关于x 的不等式f (x )≤1的解集为( )A ．(－∞，－3]∪[－1，＋∞)B ．[－3，－1]C ．[－3，－1]∪(0，＋∞)D ．[－3，＋∞)答案　C解析　当x ≤0时，f (x )＝x 2＋bx ＋c 且f (－4)＝f (0)，故其对称轴为x ＝－＝－2，b 2∴b ＝4．又f (－2)＝4－8＋c ＝0，∴c ＝4．当x ≤0时，令x 2＋4x ＋4≤1，有－3≤x ≤－1；当x >0时，f (x )＝－2≤1显然成立，故不等式的解集为[－3，－1]∪(0，＋∞)．10．设a ∈R ，关于x 的不等式ax 2＋(1－2a )x －2>0的解集有下列四个命题：①原不等式的解集不可能为∅；②若a ＝0，则原不等式的解集为(2，＋∞)；③若a <－，则原不等式的解集为；④若a >0，则原不等式的解集为－∞，－12(－1a ，2)∪(2，＋∞)．1a其中正确命题的个数为( )A ．1B ．2C ．3D ．4答案　C解析　原不等式等价于(ax ＋1)(x －2)>0．当a ＝0时，不等式化为x －2>0，得x >2．当a ≠0时，方程(ax ＋1)·(x －2)＝0的两根分别是2和－，若a <－，解不1a 12等式得－<x <2；若a ＝－，不等式的解集为∅；若－<a <0，解不等式得2<x <－；1a 12121a若a >0，解不等式得x <－或x >2．故①为假命题，②③④为真命题．1a11．若不等式－3≤x 2－2ax ＋a ≤－2有唯一解，则a 的值是( )A ．2或－1B ．－1±52C ． D ．21±52答案　A解析　令f (x )＝x 2－2ax ＋a ，即f (x )＝(x －a )2＋a －a 2，因为－3≤x 2－2ax ＋a ≤－2有唯一解，所以a －a 2＝－2，即a 2－a －2＝0，解得a ＝2或a ＝－1．故选A ．12．已知三个不等式：①x 2－4x ＋3<0，②x 2－6x ＋8<0，③2x 2－9x ＋m <0．要使同时满足①②的所有x 的值满足③，则m 的取值范围为________．答案　m ≤9解析　由①②得2<x <3，要使同时满足①②的所有x 的值满足③，即不等式2x 2－9x ＋m <0在x ∈(2，3)上恒成立，即m <－2x 2＋9x 在x ∈(2，3)上恒成立，又－2x 2＋9x 在x ∈(2，3)上大于9，所以m ≤9．二、高考小题13．(经典浙江高考)已知函数f (x )＝x 3＋ax 2＋bx ＋c ，且0<f (－1)＝f (－2)＝f (－3)≤3，则( )A ．c ≤3B ．3<c ≤6C ．6<c ≤9D ．c >9。

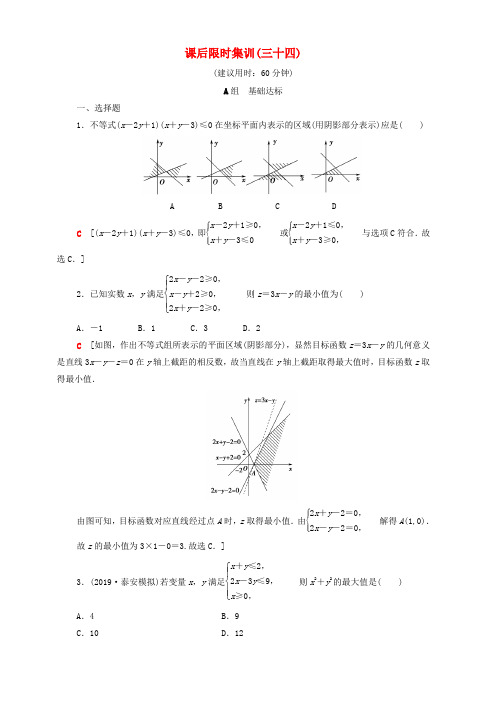
课后限时集训(三十四)(建议用时：60分钟) A 组 基础达标一、选择题1．不等式(x －2y ＋1)(x ＋y －3)≤0在坐标平面内表示的区域(用阴影部分表示)应是( )A B C DC [(x －2y ＋1)(x ＋y －3)≤0，即⎩⎪⎨⎪⎧x －2y ＋1≥0，x ＋y －3≤0或⎩⎪⎨⎪⎧x －2y ＋1≤0，x ＋y －3≥0，与选项C 符合．故选C ．]2．已知实数x ，y 满足⎩⎪⎨⎪⎧2x －y －2≥0，x －y ＋2≥0，2x ＋y －2≥0，则z ＝3x －y 的最小值为( )A ．－1B ．1C ．3D ．2C [如图，作出不等式组所表示的平面区域(阴影部分)，显然目标函数z ＝3x －y 的几何意义是直线3x －y －z ＝0在y 轴上截距的相反数，故当直线在y 轴上截距取得最大值时，目标函数z 取得最小值．由图可知，目标函数对应直线经过点A 时，z 取得最小值．由⎩⎪⎨⎪⎧2x ＋y －2＝0，2x －y －2＝0，解得A (1,0)．故z 的最小值为3×1－0＝3.故选C ．]3．(2019·泰安模拟)若变量x ，y 满足⎩⎪⎨⎪⎧x ＋y ≤2，2x －3y ≤9，x ≥0，则x 2＋y 2的最大值是( )A ．4B ．9C ．10D ．12C [作出不等式组表示的平面区域，如图中阴影部分所示．x 2＋y 2表示平面区域内的点到原点距离的平方，由⎩⎪⎨⎪⎧x ＋y ＝2，2x －3y ＝9得A (3，－1)，由图易得(x 2＋y 2)max ＝|OA |2＝32＋(－1)2＝10.故选C ．]4．(2019·衡阳模拟)若x ，y 满足⎩⎪⎨⎪⎧x ＋y ≥1，mx －y ≤0，3x －2y ＋2≥0且z ＝3x －y 的最大值为2，则实数m的值为( )A ．13 B ．23 C ．1D ．2D [由选项得m ＞0，作出不等式组⎩⎪⎨⎪⎧x ＋y ≥1，mx －ym ＞，3x －2y ＋2≥0表示的平面区域，如图中阴影部分．因为z ＝3x －y ，所以y ＝3x －z ，当直线y ＝3x －z 经过点A 时，直线在y 轴上的截距－z 最小，即目标函数取得最大值2.由⎩⎪⎨⎪⎧3x －2y ＋2＝0，3x －y ＝2，得A (2,4)，代入直线mx －y ＝0得2m －4＝0，所以m ＝2.]5．某企业生产甲、乙两种产品均需用A ，B 两种原料，已知生产1吨每种产品所需原料及每天原料的可用限额如表所示，如果生产1吨甲、乙产品可获利润分别为3万元、4万元，则该企业每天可获得最大利润为( )A C ．17万元D ．18万元D [设每天生产甲、乙产品分别为x 吨、y 吨，每天所获利润为z 万元，则有⎩⎪⎨⎪⎧3x ＋2y ≤12，x ＋2y ≤8，x ≥0，y ≥0，目标函数z ＝3x ＋4y ，线性约束条件表示的可行域如图阴影部分所示：可得目标函数在点A 处取到最大值．由⎩⎪⎨⎪⎧x ＋2y ＝8，3x ＋2y ＝12得A (2,3)．则z max ＝3×2＋4×3＝18(万元)．] 二、填空题6．(2017·全国卷Ⅲ)若x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y －2≤0，y ≥0，则z ＝3x －4y 的最小值为________．－1 [不等式组⎩⎪⎨⎪⎧x －y ≥0，x ＋y －2≤0，y ≥0表示的可行域如图阴影部分所示．由z ＝3x －4y 得y ＝34x －14z .平移直线y ＝34x ，易知经过点A 时，z 有最小值．由⎩⎪⎨⎪⎧x －y ＝0，x ＋y －2＝0得⎩⎪⎨⎪⎧x ＝1，y ＝1，∴A (1,1)．∴z min ＝3－4＝－1.]7．若变量x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ＋1≤0，y ≤1，x ＞－1，则(x －2)2＋y 2的最小值为________．5 [作出不等式组对应的平面区域如图阴影部分所示，设z ＝(x －2)2＋y 2，则z 的几何意义为区域内的点到定点D (2,0)的距离的平方， 由图知C ，D 间的距离最小，此时z 最小．由⎩⎪⎨⎪⎧y ＝1，x －y ＋1＝0得⎩⎪⎨⎪⎧x ＝0，y ＝1，即C (0,1)，此时z min ＝(x －2)2＋y 2＝4＋1＝5.]8．已知实数x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2，则目标函数z ＝y ＋2x －5的最大值为________． －12[作出约束条件所表示的平面区域，其中A (0,1)，B (1,0)，C (3,4)．目标函数z ＝y ＋2x －5表示过点Q (5，－2)与点(x ，y )的直线的斜率，且点(x ，y )在△ABC 平面区域内．显然过B ，Q 两点的直线的斜率z 最大，最大值为0＋21－5＝－12.]三、解答题9．如图所示，已知D 是以点A (4,1)，B (－1，－6)，C (－3,2)为顶点的三角形区域(包括边界与内部)．(1)写出表示区域D 的不等式组；(2)设点B (－1，－6)，C (－3,2)在直线4x －3y －a ＝0的异侧，求a 的取值范围．[解] (1)直线AB ，AC ，BC 的方程分别为7x －5y －23＝0，x ＋7y －11＝0,4x ＋y ＋10＝0.原点(0,0)在区域D 内，故表示区域D 的不等式组为⎩⎪⎨⎪⎧7x －5y －23≤0，x ＋7y －11≤0，4x ＋y ＋10≥0.(2)根据题意有[4×(－1)－3×(－6)－a ]·[4×(－3)－3×2－a ]＜0，即(14－a )(－18－a )＜0，解得－18＜a ＜14.故a 的取值范围是(－18,14)．10．若x ，y 满足约束条件⎩⎪⎨⎪⎧x ＋y ≥1，x －y ≥－1，2x －y ≤2.(1)求目标函数z ＝12x －y ＋12的最值；(2)若目标函数z ＝ax ＋2y 仅在点(1,0)处取得最小值，求a 的取值范围． [解] (1)作出可行域如图，可求得A (3,4)，B (0,1)，C (1,0)．平移初始直线12x －y ＋12＝0，过A (3,4)时z 取最小值－2，过C (1,0)时z 取最大值1.所以z 的最大值为1，最小值为－2.(2)直线ax ＋2y ＝z 仅在点(1,0)处取得最小值，由图像可知－1＜－a2＜2，解得－4＜a ＜2.故a 的取值范围是(－4,2)．B 组 能力提升1．若平面区域⎩⎪⎨⎪⎧x ＋y －3≥0，2x －y －3≤0，x －2y ＋3≥0夹在两条斜率为1的平行直线之间，则这两条平行直线间的距离的最小值是( )A ．355 B. 2 C ．322D. 5B [根据约束条件作出可行域如图阴影部分，当斜率为1的直线分别过A 点和B 点时满足条件，联立方程组⎩⎪⎨⎪⎧x ＋y －3＝0，x －2y ＋3＝0求得A (1,2)，联立方程组⎩⎪⎨⎪⎧2x －y －3＝0，x ＋y －3＝0求得B (2,1)，可求得分别过A ，B 点且斜率为1的两条直线方程为x －y ＋1＝0和x －y －1＝0，由两平行线间的距离公式得距离为|1＋1|2＝2，故选B.]2．若不等式组⎩⎪⎨⎪⎧x ＋y －2≤0，x ＋2y －2≥0，x －y ＋2m ≥0表示的平面区域为三角形，且其面积等于43，则m 的值为( )A ．－3B ．1C ．43D ．3B [作出可行域，如图中阴影部分所示，易求A ，B ，C ，D 的坐标分别为A (2,0)，B (1－m,1＋m )，C 2－4m 3，2＋2m3，D (－2m,0)．S △ABC ＝S △ADB －S △ADC ＝12|AD |·|y B －y C |＝12(2＋2m )·⎝⎛⎭⎪⎫1＋m －2＋2m 3＝(1＋m )⎝ ⎛⎭⎪⎫1＋m －23＝43，解得m ＝1或m ＝－3(舍去)．]3．已知实数x ，y 满足⎩⎪⎨⎪⎧2x ＋y ≥0，x －y ≥0，0≤x ≤a ，设b ＝x －2y ，若b 的最小值为－2，则b 的最大值为__________．10 [画出可行域，如图阴影部分所示．由b ＝x －2y ，得y ＝12x －b2.易知在点(a ，a )处b 取最小值，故a －2a ＝－2，可得a ＝2.在点(2，－4)处b 取最大值，于是b 的最大值为2＋8＝10.]4．某化肥厂生产甲、乙两种混合肥料，需要A ，B ，C 三种主要原料．生产1车皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如下表所示：原料肥料ABC甲 4 8 3 乙5510现有A 已知生产1车皮甲种肥料，产生的利润为2万元；生产1车皮乙种肥料，产生的利润为3万元．分别用x ，y 表示计划生产甲、乙两种肥料的车皮数．(1)用x ，y 列出满足生产条件的数学关系式，并画出相应的平面区域；(2)问分别生产甲、乙两种肥料各多少车皮，能够产生最大的利润？并求出此最大利润．[解] (1)由已知，x ，y 满足的数学关系式为⎩⎪⎨⎪⎧4x ＋5y ≤200，8x ＋5y ≤360，3x ＋10y ≤300，x ≥0，y ≥0.该二元一次不等式组所表示的平面区域为图①中的阴影部分．(2)设利润为z 万元，则目标函数为z ＝2x ＋3y .考虑z ＝2x ＋3y ，将它变形为y ＝－23x ＋z 3，它的图像是斜率为－23，随z 变化的一组平行直线，z3为直线在y 轴上的截距，当z3取最大值时，z 的值最大．根据x ，y 满足的约束条件，由图②可知，当直线z ＝2x ＋3y 经过可行域上的点M 时，截距z3最大，即z 最大．解方程组⎩⎪⎨⎪⎧4x ＋5y ＝200，3x ＋10y ＝300，得点M 的坐标为(20,24)，所以z max ＝2×20＋3×24＝112.即生产甲种肥料20车皮，乙种肥料24车皮时利润最大，且最大利润为112万元．。

课后限时集训(三十四) 基本不等式(建议用时：60分钟) A 组 基础达标一、选择题1．“x ≥1”是“x ＋1x≥2”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件A [x ＋1x ≥2⇔x ＞0，所以“x ≥1”是“x ＋1x≥2”的充分不必要条件，故选A.]2．已知x ＞0，y ＞0，且4x ＋y ＝xy ，则x ＋y 的最小值为( ) A ．8 B ．9 C ．12D ．16B [由4x ＋y ＝xy 得4y ＋1x＝1，则x ＋y ＝(x ＋y )⎝ ⎛⎭⎪⎫4y ＋1x ＝4x y ＋yx＋1＋4≥24＋5＝9，当且仅当4x y ＝yx，即x ＝3，y ＝6时取“＝”，故选B.]3．已知x ＞0，y ＞0，lg 2x ＋lg 8y＝lg 2，则1x ＋13y 的最小值为( )A ．2B ．2 2C ．4D ．23C [∵lg 2x＋lg 8y＝lg(2x·8y) ＝lg 2x ＋3y＝lg 2，∴2x ＋3y＝2，即x ＋3y ＝1.∵x ＞0，y ＞0，∴1x ＋13y ＝⎝ ⎛⎭⎪⎫1x ＋13y (x ＋3y )＝2＋3y x ＋x3y ≥2＋23y x ·x3y＝4， 当且仅当x ＝3y ＝12时等号成立．∴1x ＋13y的最小值为4.故选C.] 4．设a ＞1，b ＞1，且ab －(a ＋b )＝1，那么( ) A ．a ＋b 有最小值2(2＋1) B ．a ＋b 有最大值(2＋1)2C ．ab 有最大值2＋1D ．ab 有最小值2(2＋1) A [因为ab －(a ＋b )＝1，ab ≤⎝⎛⎭⎪⎫a ＋b 22，所以⎝⎛⎭⎪⎫a ＋b 22－(a ＋b )≥1，它是关于a ＋b 的一元二次不等式，解得a ＋b ≥2(2＋1)或a ＋b ≤2(1－2)(舍去)，又因为ab －(a ＋b )＝1，a ＋b ≥2ab ，所以ab －2ab ≥1，它是关于ab 的一元二次不等式， 解得ab ≥2＋1或ab ≤1－2(舍去)， 所以ab ≥3＋22，即ab 有最小值3＋2 2.]5．已知关于x 的不等式x 2－4ax ＋3a 2＜0(a ＜0)的解集为(x 1，x 2)，则x 1＋x 2＋ax 1x 2的最大值是( ) A.63 B.233 C.433D ．－433D [∵不等式x 2－4ax ＋3a 2＜0(a ＜0)的解集为(x 1，x 2)，∴在方程x 2－4ax ＋3a 2＝0中，由根与系数的关系知x 1x 2＝3a 2，x 1＋x 2＝4a ，则x 1＋x 2＋a x 1x 2＝4a ＋13a .∵a ＜0，∴－⎝⎛⎭⎪⎫4a ＋13a ≥24a ×13a ＝433，即4a ＋13a ≤－433，故x 1＋x 2＋a x 1x 2的最大值为－433.故选D]二、填空题 6．若对任意x ＞0，xx 2＋3x ＋1≤a 恒成立，则a 的取值范围是________．⎣⎢⎡⎭⎪⎫15，＋∞ [∵对任意x ＞0，x x 2＋3x ＋1≤a 恒成立， ∴对x ∈(0，＋∞)，a ≥⎝ ⎛⎭⎪⎫x x 2＋3x ＋1max，而对x ∈(0，＋∞)，xx 2＋3x ＋1＝1x ＋1x＋3≤12x ·1x＋3＝15， 当且仅当x ＝1x 时等号成立，∴a ≥15.]7．(2019·石家庄模拟)已知正数a ，b 满足4a ＋b ＝30，使得1a ＋4b取最小值的实数对(a ，b )是________．⎝ ⎛⎭⎪⎫154，15 [∵正数a ，b 满足4a ＋b ＝30， ∴1a ＋4b ＝130(4a ＋b )⎝ ⎛⎭⎪⎫1a ＋4b ＝130⎝ ⎛⎭⎪⎫8＋b a ＋16a b ≥130×⎝ ⎛⎭⎪⎫8＋2b a ·16a b ＝815， 当且仅当b ＝4a ＝15时，取等号．∴使得1a ＋4b 取最小值的实数对(a ，b )是⎝ ⎛⎭⎪⎫154，15.]8．某公司一年购买某种货物600吨，每次购买x 吨，运费为6万元/次，一年的总存储费用为4x 万元，要使一年的总运费与总存储费用之和最小，则x 的值是________．30 [一年的总运费为6×600x ＝3 600x(万元)．一年的总存储费用为4x 万元． 总运费与总存储费用的和为⎝ ⎛⎭⎪⎫3 600x ＋4x 万元．因为3 600x＋4x ≥23 600x·4x ＝240，当且仅当3 600x＝4x ，即x ＝30时取得等号，所以当x ＝30时，一年的总运费与总存储费用之和最小．] 三、解答题9．已知x ＞0，y ＞0，且2x ＋5y ＝20. (1)求u ＝lg x ＋lg y 的最大值； (2)求1x ＋1y的最小值．[解] (1)因为x ＞0，y ＞0，所以由基本不等式，得2x ＋5y ＝20≥210xy .即xy ≤10，当且仅当2x ＝5y 时等号成立，此时x ＝5，y ＝2， 所以u ＝lg x ＋lg y ＝lg(xy )≤lg 10＝1.所以当x ＝5，y ＝2时，u ＝lg x ＋lg y 有最大值1.(2)因为x ＞0，y ＞0，所以1x ＋1y ＝⎝ ⎛⎭⎪⎫1x ＋1y ·2x ＋5y 20＝120⎝ ⎛⎭⎪⎫7＋5y x ＋2x y ≥120⎝ ⎛⎭⎪⎫7＋25y x·2x y ＝7＋21020，当且仅当5y x ＝2xy 时等号成立． 所以1x ＋1y 的最小值为7＋21020.10．某厂家拟在2019年举行某产品的促销活动，经调查测算，该产品的年销售量(即该厂的年产量)x 万件与年促销费用m 万元(m ≥0)满足x ＝3－km ＋1(k 为常数)，如果不搞促销活动，则该产品的年销售量只能是1万件．已知生产该产品的固定投入为8万元，每生产一万件该产品需要再投入16万元，厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)．(1)将2019年该产品的利润y 万元表示为年促销费用m 万元的函数； (2)该厂家2019年的促销费用投入多少万元时，厂家的利润最大？ [解] (1)由题意知，当m ＝0时，x ＝1(万件)， 则1＝3－k ，解得k ＝2，∴x ＝3－2m ＋1. ∵每件产品的销售价格为1.5×8＋16xx(元)，∴2018年的利润y ＝1.5x ×8＋16x x －8－16x －m ＝－⎣⎢⎡⎦⎥⎤16m ＋1＋m ＋＋29(m ≥0)．(2)∵当m ≥0时，m ＋1＞0，∴16m ＋1＋(m ＋1)≥216＝8，当且仅当m ＝3时等号成立． ∴y ≤－8＋29＝21， 当且仅当16m ＋1＝m ＋1，即m ＝3万元时，y max ＝21(万元)． 故该厂家2019年的促销费用投入3万元时，厂家的利润最大为21万元．B 组 能力提升1．若x ＜12，则f (x )＝12x －1＋4x ( )A ．有最小值2＋2 2B ．有最大值2＋2 2C ．有最小值2－2 2D ．有最大值2－22D [由题可知，f (x )＝12x －1＋2(2x －1)＋2，因为x ＜12，所以2x －1＜0.所以12x －1＋2(2x －1)＝－[2(1－2x )＋11－2x ]≤－2－2x11－2x＝－22， 当且仅当12x －1＝2(2x －1)，即x ＝2－24时等号成立．所以f (x )≤2－22，即f (x )有最大值2－2 2.]2．(2019·西安模拟)若△ABC 的内角满足sin A ＋2sin B ＝2sin C ，则cos C 的最小值是( ) A.6－24 B.6＋24 C.6－22D.6＋22A [由正弦定理，得a ＋2b ＝2c .所以cos C ＝a 2＋b 2－c 22ab＝a 2＋b 2－⎝⎛⎭⎪⎫a ＋2b 222ab＝3a 2＋2b 2－22ab 8ab≥26ab －22ab 8ab ＝6－24.当且仅当3a 2＝2b 2，即3a ＝2b 时，等号成立． 所以cos C 的最小值为6－24.] 3．(2018·天津高考)已知a ，b ∈R，且a －3b ＋6＝0，则2a＋18b 的最小值为________．14 [∵a －3b ＝－6，∴2a ＋18b ＝2a ＋2－3b≥22a ·2－3b＝22a －3b＝22－6＝2×2－3＝14，当且仅当⎩⎪⎨⎪⎧a ＝－3b ，a －3b ＋6＝0，即a ＝－3，b ＝1时等号成立．]4．(2019·成都诊断)某工厂需要建造一个仓库，根据市场调研分析，运费与工厂和仓库之间的距离成正比，仓储费与工厂和仓库之间的距离成反比，当工厂和仓库之间的距离为4千米时，运费为20万元，仓储费为5万元，当工厂和仓库之间的距离为多少千米时，运费与仓储费之和最小，最小为多少万元？[解] 设工厂和仓库之间的距离为x 千米，运费为y 1万元，仓储费为y 2万元，则y 1＝k 1x (k 1≠0)，y 2＝k 2x(k 2≠0)，∵工厂和仓库之间的距离为4千米时，运费为20万元，仓储费用为5万元， ∴k 1＝5，k 2＝20，∴运费与仓储费之和为⎝ ⎛⎭⎪⎫5x ＋20x 万元，∵5x ＋20x≥25x ×20x ＝20，当且仅当5x ＝20x，即x ＝2时，运费与仓储费之和最小，为20万元．。

课时作业34 一元二次不等式及其解法8．不等式x －22x －3x ＋1<0的解集为( )A ．{x |－1<x <2或2<x <3}B ．{x |1<x <3}C ．{x |2<x <3}D ．{x |－1<x <3}解析：原不等式⇔⎩⎪⎨⎪⎧ x ＋1x －3<0，x －2≠0，∴－1<x <3且x ≠2.答案：A9．如果A ＝{x |ax 2－ax ＋1<0}＝∅，则实数a 的取值集合为( )A ．{a |0<a <4}B ．{a |0≤a <4}C ．{a |0<a ≤4} D．{a |0≤a ≤4}解析：当a ＝0时，有1<0，故A ＝∅.当a ≠0时，若A ＝∅，则有⎩⎪⎨⎪⎧ a >0，Δ＝a 2－4a ≤0，解得0<a ≤4.综上，a 的取值集合为{a |0≤a ≤4}．答案：D10．[2019·昆明模拟]不等式x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，则实数a 的取值范围为( )A ．[－1,4]B ．(－∞，－2]∪[5，＋∞)C ．(－∞，－1]∪[4，＋∞)D ．[－2,5]解析：x 2－2x ＋5＝(x －1)2＋4的最小值为4，所以x 2－2x ＋5≥a 2－3a 对任意实数x 恒成立，只需a 2－3a ≤4，解得－1≤a ≤4.答案：A二、填空题11．二次函数y ＝x 2－4x ＋3在y <0时x 的取值范围是________．解析：依题意，得x 2－4x ＋3<0，即(x －1)·(x －3)<0.∴1<x <3.答案：(1,3)12．不等式组⎩⎪⎨⎪⎧ x x ＋2>0，|x |<1的解集为________．解析：原不等式组可化为⎩⎪⎨⎪⎧ x <－2或x >0，－1<x <1，解得0<x <1.答案：{x |0<x <1}13．若关于x 的不等式x 2－3x ＋t <0的解集为{x |1<x <m ，x ∈R }，则t ＋m ＝________. 解析：∵ 不等式x 2－3x ＋t <0的解集为{x |1<x <m ，x ∈R }，∴1，m 是方程x 2－3x ＋t ＝0的两根，∴⎩⎪⎨⎪⎧1＋m ＝3m ＝t ，解得⎩⎪⎨⎪⎧ m ＝2t ＝2. ∴t ＋m ＝4. 答案：4 14．不等式x 2＋ax ＋4<0的解集不是空集，则实数a 的取值范围是________．解析：∵不等式x 2＋ax ＋4<0的解集不是空集，∴Δ＝a 2－4×4>0，即a 2>16.∴a >4或a <－4.答案：(－∞，－4)∪(4，＋∞) [能力挑战]15．在R 上定义运算: 若不等式(x －a ) (x ＋a )<1对任意的实数x ∈R 恒成立，则实数a 的取值范围是( )A.－1<a <1 B ．0<a <2C.－12<a <32 D ．－32<a <12答案：C16.若关于x 的一元二次不等式ax 2＋bx ＋c <0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪ x <13或x >12，则关于x 的不等式cx 2－bx ＋a >0的解集为________．解析：由题意知⎩⎪⎨⎪⎧a <0，13＋12＝－b a ，13×12＝c a ，所以⎩⎪⎨⎪⎧a <0，b ＝－56a >0，c ＝16a <0，代入不等式cx 2－bx ＋a >0中得16ax 2＋56ax 即16x 2＋56x ＋1<0，化简得x 2＋5x ＋6<0，＋a >0(a <0)．所以所求不等式的解集为{x |－3<x <－2}．答案：(－3，－2)17.若不等式x 2＋mx －1<0对于任意x ∈[m ，m ＋1]都成立，则实数m 的取值范围是________． 解析：由题意，得函数f (x )＝x 2＋mx －1在[m ，m ＋1]上的最大值小于0，又抛物线f (x )＝x 2＋mx －1开口向上， 所以只需⎩⎪⎨⎪⎧ f m ＝m 2＋m 2－1<0，fm ＋1＝m ＋12＋m m ＋1－1<0， 即⎩⎪⎨⎪⎧ 2m 2－1<0，2m 2＋3m <0，解得－22<m <0. 答案：⎝ ⎛⎭⎪⎫－22，0。

考点34 数学归纳法1．（2019·江苏高三高考模拟）已知数列{}n a ，12a =，且211n n n a a a +=-+对任意n N *∈恒成立．（1）求证：112211n n n n a a a a a a +--=+(n N *∈)；（2）求证：11nn a n +>+(n N *∈)． 【答案】（1）见解析（2）见解析 【解析】（1）①当1n =时，2221112213a a a =-+=-+= 满足211a a =+成立.②假设当n k =时，结论成立.即：112211k k k k a a a a a a +--=+成立下证：当1n k =+时，112211k k k k a a a a a a +-+=+成立。

因为()211211111k k k k k a a a a a +++++=-+-+=()()11221112211111k k k k k k k k a a a a a a a a a a a a +--+--=+=++-即：当1n k =+时，112211k k k k a a a a a a +-+=+成立由①、②可知，112211n n n n a a a a a a +--=+(n *N ∈)成立。

（2）（ⅰ）当1n =时，221221311a >=-=++成立，当2n =时，()2322222172131112a a a a a =-+=-+=>⨯>++成立，（ⅱ）假设n k =时（3k ≥），结论正确，即：11kk a k +>+成立 下证：当1n k =+时，()1211k k a k ++>++成立.因为()()2211112111111kkkk k k k k k a a a a a k k kk +++++-+==-+>++=++要证()1211k k a k ++>++，只需证()12111k k k k k k +++>++只需证：()121k k k k ++>，只需证：()12ln ln 1k k k k ++>即证：()()12l l n n 10k k k k -++>（3k ≥） 记()()()2ln 11ln h x x x x x -++=∴()()()()2ln 1112ln 11ln ln x x x x h x +-++=-++⎡⎤⎦=⎣' 21ln 1ln 12111x x x x ⎛⎫=+=++-+ ⎪++⎝⎭当12x +≥时，1111ln 121ln 221ln 1ln 10122x x e ⎛⎫⎛⎫++-+≥+-+=+>+= ⎪ ⎪+⎝⎭⎝⎭所以()()()2ln 11ln h x x x x x -++=在[)1,+∞上递增， 又()6423ln34ln3ln 34ln729ln2564l 0n h ⨯-=-=->=所以，当3x ≥时，()()30h x h ≥>恒成立。

2018版高考数学一轮复习第六章数列课时跟踪检测34 理新人教A版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018版高考数学一轮复习第六章数列课时跟踪检测34 理新人教A版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018版高考数学一轮复习第六章数列课时跟踪检测34 理新人教A版的全部内容。

课时跟踪检测(三十四)[高考基础题型得分练］1．［2017·四川绵阳一诊]已知数列{a n｝的通项公式是a n＝2n－3错误!n，则其前20项和为( )A．380－错误!错误!B．400－错误!错误!C．420－错误!错误!D．440－错误!错误!答案：C解析:令数列｛a n｝的前n项和为S n，则S20＝a1＋a2＋…＋a20＝2(1＋2＋…＋20)－3错误!＝2×20×20＋12－3×错误!＝420－错误!错误!。

2．已知数列｛a n}是首项为1的等比数列，S n是{a n}的前n项和,且9S3＝S6，则数列错误!的前5项和为( )A.错误!或5 B．错误!或5C。

错误!D．错误!答案：C解析：设{a n}的公比为q，显然q≠1，由题意，得错误!＝错误!,所以1＋q3＝9,解得q＝2,所以错误!是首项为1,公比为错误!的等比数列，则所求的前5项和为错误!＝错误!.3．数列{a n｝的通项公式为数列a n＝错误!,其前n项和为错误!,则在平面直角坐标系中,直线（n＋1)x＋y＋n＝0在y轴上的截距为（）A．－10 B．－9C．10 D．9答案：B解析:数列的前n项和为错误!＋错误!＋…＋错误!＝1－错误!＝错误!＝错误!，解得n＝9，∴直线方程为10x＋y＋9＝0.令x＝0，得y＝－9，∴在y轴上的截距为－9.4．数列{a n｝的通项公式为a n＝（－1）n－1·(4n－3），则它的前100项和S100＝（) A．200 B．－200C．400 D．－400答案：B解析：S100＝(4×1－3)－（4×2－3)＋（4×3－3)－…－（4×100－3）＝4×[（1－2）＋(3－4)＋…＋（99－100）]＋[－3－(－3)－3＋…－（－3）］＝4×（－50）＝－200。