低维带参非线性狄拉克方程

非线性微分方程的天体物理学方程非线性微分方程在物理领域中应用十分广泛，特别是在天体物理学中的应用更为突出。

对于非线性微分方程的研究，有助于我们更好地理解和探索天体物理学的规律和现象。

本文将重点探讨非线性微分方程在天体物理学中的应用。

1. 引言天体物理学的研究是一门综合性学科，它研究的范围涵盖了整个宇宙。

在这个过程中，数学是必不可少的工具。

其中，非线性微分方程是天体物理学中常用的数学工具之一。

通过对非线性微分方程的研究，我们能更好地去揭示宇宙中的奥秘。

接下来，我们介绍一些常见的非线性微分方程及其在天体物理学中的应用。

2. Lorenz方程Lorenz方程是非线性微分方程的代表之一。

它的形式为：$$\frac{dx}{dt}=\sigma(y-x)$$$$\frac{dy}{dt}=x(\rho-z)-y$$$$\frac{dz}{dt}=xy-\beta z$$其中，$x$，$y$，$z$ 是三个变量，$\sigma$，$\rho$，$\beta$ 是参数。

Lorenz方程在物理领域中的应用非常广泛，尤其在大气科学中的天气预报方面。

此外，它还可以用来描述流体、火焰等多种非定常系统的行为。

在天体物理学中，Lorenz方程被广泛应用于天体演化的模拟和研究中。

利用Lorenz方程可以建立天体演化的数值模拟模型，研究各种天体现象，如行星、恒星等的形成、演化。

同时，Lorenz 方程也可以用于分析星际介质（ISM）的动力学行为和自旋的转移等。

3. Van der Pol方程Van der Pol方程是一种带有非线性阻尼的非线性微分方程，它的形式为：$$\frac{d^2x}{dt^2}+\mu(x^2-1)\frac{dx}{dt}+x=0$$其中，$\mu$ 是参数。

Van der Pol方程在电气工程、生物学、物理学等多个领域都有着广泛的应用。

在天体物理学中，Van der Pol方程可以用来描述黑洞的重力红移现象。

狄拉克δ函数格林函数本文以狄拉克δ函数、格林函数为标题，旨在探讨它们的特性和应用，以及它们之间的联系。

狄拉克δ函数（Delta function）是一种特殊的函数，描述了一个值围绕某一点变化的情况。

它最初由马可狄拉克于1937年发明，供于研究物理过程的数学模型，它具有下面的特性：（1）它是一种分布式函数，其值在一个点（0点）达到极大，其他位置的值都是0；（2）它满足积分分布定理，即其积分为恒定值；（3）它可以用来描述在连续变化的过程中分量的变化情况。

狄拉克δ函数主要用于分析物理规律，最常用的例子是用来分析受力的情况，这也是其被更多人研究的原因。

由于其独特的特性，狄拉克δ函数得到了在物理学中广泛的应用，比如质能守恒定律、动量守恒定律、牛顿的第二定律等。

格林函数（Green’s function）是一种用以描述一般线性系统的方法，它描述了系统在特定情况下最终时刻的状态。

它是一种泛函，可用来解决种类繁多的低维空间的线性微分方程组。

格林函数广泛应用于几何和微分几何中，用于解决各种类型的线性偏微分方程，可被用来解决物理和工程等问题。

特别是在物理和电路仿真中，格林函数被用来描述某些特定系统的响应，以及在这些系统中解决一些具体科学问题。

另外，由于狄拉克δ函数和格林函数都可以用来描述线性系统的响应，它们之间相互作用也很重要，它们可以用来求解数学和物理问题，尤其是在处理非线性系统方面更是如此。

此外，许多现代物理学和数学模型都借鉴了狄拉克δ函数和格林函数的思想，用于分析和解决相应的问题。

综上所述，狄拉克δ函数和格林函数都是十分重要的函数，它们可以用来求解许多常见的数学和物理问题。

它们的应用以及它们之间的联系，可以让我们更好地理解宇宙中的物理现象，提高我们对物理概念的认识，为我们解决实际问题提供有效的方法。

（1）石墨烯电子狄拉克方程之数理演绎 （2015年5月1日）作者： 北京东之星应用物理研究所伍 勇 ， 贺 宁（计算机软件工程师）1. 量子场论中狄拉克方程的引出非相对论量子力学中，速度c v <<的自由粒子运动状态ψ由薛定谔方程描述（自然单位1==c ）：从能量-动量色散关系mp E 22=，对应算符变换：tiE ∂∂>- ∇->-i p容易导出自由粒子薛定谔波动方程：ψ∇-=ψ∂∂mt 2i 2 当c v ~，粒子服从相对论量子力学能量-动量色散关系222m p E+= , 由上述算符对应关系可建立场ψ 的克莱因-戈登（Klein-Gordon ）相对论波动方程,又称KG 方程：ψ=ψ∂∂-∇2222)t(m （2）或 0)(22=ψ-m 口其中， 2222t ∂∂-∇=口狄拉克凭借理论直觉，对（2）两端做形式开方，以维持算符线性化（对t 二次微商会导致负几率困难）得到：ψ+∇⋅-=ψ∂∂)(i m i t βα , m i H βα+∇⋅-=（3） 这就是三维自由粒子的狄拉克方程（Dirac equation ）。

态函数ψ是函数空间和4维自旋空间的直积空间中的矢量，比例参量α，β的形式和性质如是：⎥⎦⎤⎢⎣⎡=00jj j σσα )3,2,1(=j , ⎥⎦⎤⎢⎣⎡-=I I 00β ，其中I 为2X2单位矩阵， 三个泡利矩阵⎥⎦⎤⎢⎣⎡=01101σ ， ⎥⎦⎤⎢⎣⎡-=002i i σ ， ⎥⎦⎤⎢⎣⎡-=10013σ（4） 易证：122i==βα,i αα=+i ,ββ=+0},{=+≡i j j i j i αααααα j i ≠ 0},{=βαi引入：⎩⎨⎧=-==βγβαγ4jj i)3,2,1(=j 可将狄拉克方程（3）写成四维形式：)(=ψ+∂m μμγ4,3,2,1=μ（5）这里),(),,,(432,1it x x x x x x==μ，μμx ∂∂≡∂证明(3),(5)的一致性如下： 方程(3)乘(β-) ; (β-)0)i(=ψ-∇⋅+∂∂m i t βα方程左端有m x x m x i it jj j j +∂∂+∂∂=+∂∂-∂∂γγβαβ44))(( 于是由（3）导出（5）。

第8章狄拉克(Dirac) 函数1.数理方程的定解问题：uu12.点源：3.连续分布的源所产生的场：注意：238.1 一维函数的定义和性质一、一维函数的定义l线电荷密度总电量4把定义在区间上，满足上述这两个要求的函数称为函数，并记作，即5时， ，所以(6)函数后，位于 处、电量为q 的点电荷的线电荷密度2m 的质点的质量线密度为：说明：1.2.67二、 函数的性质 1f(x)00())()f x x x dx f x δ+∞-∞-=（乘上f (x )f (x ) 挑选性(把f (x )在 )在 时为零，0000())())x x f x x x dx f x x x dx εεδδ+∞+-∞--=-（（时，，且时，说明：也可作为函数的定义，f(x)892.（对称性）00与 在积分号下对任一连续函数x )3. )()()()(000x x x f x x x f -=-δδ确切含义：在等式左右两边乘上任意连续函数x 积分相等104.f (x )，均有：0()()()(0)[()]0x x x f x dx xf x x dx xf x δδ∞∞=-∞=-==⎰ f (x )3中令f (x )=x ，则，则只有单根，则k个单根的区间内，。

备忘：有，则11时，有，则1213，把的每个扩大积分区间：14说明：若有重根，则上式不成立。

15三、 函数的几个常用表达式 1.—积分形式(1)(2)第12章证明：在173. —— 极限形式(1) 当 时，令 ，且有在区间的积分值：由函数定义可知：P92, 例4.2.8说明：因为函数并不是给出普通的数值之间的对应关系，所以函数也不象普通的函数那样具有唯一确定的表达式。

19207. 又因为：21四、 函数导数的定义 1.f (x )00()()()f x x x dx f x δ∞-∞''-=-称为 的导数，并记作说明： 函数的导数可按通常的导数公式进行运算222. 函数n 阶导数的定义：f (x )称为 函数的n 阶导数，并记作：23五、函数导数的性质 1是对-x 是偶函数，2f (x )乘上式左边后对x 从 到 积分，得：在积分号下对任意连续函数f (x )的运算性质相同24六、三维函数25 3. 用拉普拉斯算符表示：时， 、代入，保留对r 求的定义得：4. 正交归一完备系 的完备性条件26证明：27。

弯曲时空狄拉克方程嘿，朋友们！今天咱们来聊聊那个超级酷炫又有点让人晕头转向的弯曲时空狄拉克方程。

这方程啊，就像是宇宙这个超级大迷宫里的神秘地图。

狄拉克方程本来就像一个精致的小盒子，里面装着微观世界粒子运动的秘密。

可这弯曲时空狄拉克方程呢，就像是把这个小盒子扔到了一个巨大的、弯弯曲曲的过山车上。

你能想象吗？普通的狄拉克方程在平坦的时空里悠闲地散着步，就像一个在公园里遛弯的小老头。

而弯曲时空狄拉克方程，那可是在宇宙这个超级扭曲的大过山车上疯狂飞驰，它得同时应付那些弯弯曲曲的轨道和粒子们调皮捣蛋的行为。

它的方程看起来就像是一串神秘的魔法咒语，∇ μ(γ μD μ - m)ψ = 0。

这一大串符号啊，就像是来自外太空的信号，乍一看让人觉得像是外星生物的涂鸦。

那些γ μ就像是一群奇特的小怪兽，每个都有着自己独特的脾气和功能。

它们和D μ、m还有ψ搅和在一起，就像一场超级混乱又充满秩序的宇宙大派对。

你要是想理解这个方程，就像是试图去抓住一群在风中飞舞的彩色气球。

刚抓住一个概念，另外几个又飘走了。

比如说这个弯曲时空的概念，就像一块软绵绵的巨大棉花糖，你以为你懂了，可是稍微一用力捏，就发现它又变形了，变得让你摸不着头脑。

而狄拉克方程就在这块棉花糖里钻来钻去，寻找着粒子的踪迹。

这个方程在研究黑洞的时候就更有趣了。

黑洞就像宇宙中的超级大胃王，什么都往里吞。

而弯曲时空狄拉克方程就像是一个勇敢的探险家，试图钻进黑洞这个恐怖的大嘴巴里，去看看里面到底发生了什么。

它带着那些神秘的符号和规则，就像带着一身的魔法装备，去挑战这个宇宙中最神秘的地方。

在研究宇宙大爆炸的时候呢，弯曲时空狄拉克方程又像是一个时光回溯的侦探。

它试图从现在这些混乱的宇宙线索中，找到宇宙最初那一刻的秘密。

那些γ μ就像是侦探的小工具，D μ像是放大镜，m像是案件中的关键物证，而ψ就是那个神秘的嫌疑人，方程要做的就是把它们统统组合起来，解开宇宙诞生的谜题。

如果把宇宙比作一个超级大舞台，那么弯曲时空狄拉克方程就是那个在幕后默默操控一切的导演。

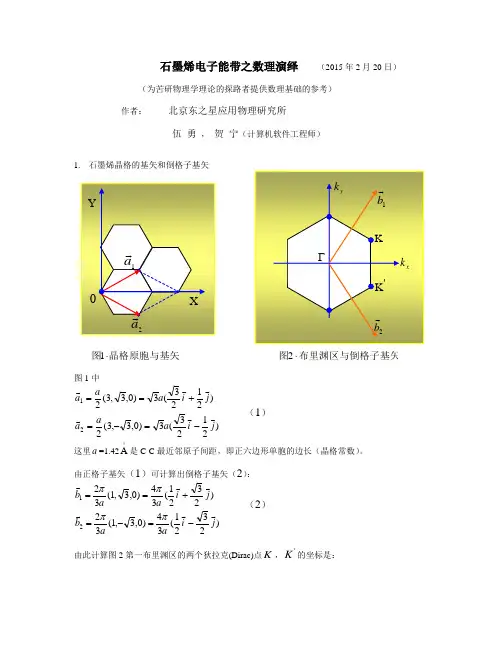
石墨烯电子能带之数理演绎 （2015年2月20日）（为苦研物理学理论的探路者提供数理基础的参考）作者： 北京东之星应用物理研究所伍 勇 ， 贺 宁（计算机软件工程师）1. 石墨烯晶格的基矢和倒格子基矢晶格原胞与基矢图⋅1 布里渊区与倒格子基矢图⋅2图1中)0,3,3(2)0,3,3(221a a a a -===这里a =1.42A 是。

由正格子基矢（122(3)0,3,1(32)0,3,1(3221a a b a b -==ππ由此计算图2第一布里渊区的两个狄拉克(Dirac)点K ，'K 的坐标是：下面能带计算表明只有第一布里渊区的六个顶点在费米面上，称费米点，又称Dirac 点或K ('K )点2. 石墨电子紧束缚近似二次量子化形式的哈密顿量∑∑><++++-+=j i j i ii i i i pz c h b a t b b a a H ,2).()(ε上式还可表为矩阵形式：⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛∑∑∑><++><++++j j j i ij pz ijpz i i j j j i i i i i i iipz b a t t b a b a t t b a b a b a ,22,2)(00)()(δεδεε模型不考虑电子自旋，<i,j >表示只对最近邻格点的电子跃迁求和，pz 2ε是单电子2pz 轨道能量石墨晶格是由两类几何环境彼此不等价的碳原子A ，B 构成，任意选定一个格点位矢是i R的A原子为参考原子，环绕它的是三个最近邻B 类原子1j R ,2j R 和3j R，如图3.+i a （j b ）是位于i R （j R ）的电子的产生（消灭）算符，（4）中的对算符+i a j b 表示的物理过程描述被j b 在j R 处消灭一个电子后又在i R 由+i a 产生一32,3.j j ji i R R R R和的三个最近邻参考原子图个电子，此过程等同于电子由j R 跃迁到最近邻i R，跃迁能t =2.8eV 。

非线性薛定谔方程的五种差分格式非线性薛定谔方程（NLSE）是一类非常重要的和高度发达的信息传输研究的重要模型。

它的出现为很多无线通信的技术发展提供了重要的基础和参照。

目前，非线性薛定谔方程的差分格式已有五种。

它们是恒定折回差分格式（CFD），动态折回差分格式（DRFD），步进步函数差分格式（SDF），连续步函数差分格式（CDF）和多阶进步函数差分格式（MSDF）。

恒定折回差分格式（CFD）是用于解决非线性薛定谔方程的最简单的一种差分格式。

它最初由Lyons发明，是一种非标准的三点迭代形式，但比一般三点迭代形式更有效。

它的优点在于最大限度地减少了计算量，但它的准确性不高，偏离正确的解。

动态折回差分格式（DRFD）是用于解决非线性薛定谔方程的一种改进的差分格式。

它使用了非标准的五点迭代形式，比三点迭代形式更高效，可以很好地跟踪参数变化并准确地加以反映。

它在计算量上比CFD稍大，但其计算结果更加准确，离正确解更近。

步进函数差分格式（SDF）是用于解决非线性薛定谔方程的一种改进的五点迭代格式。

它在数值处理上有更低的计算量，而且能够比动态折回差分格式更准确地产生数值解。

连续步函数差分格式（CDF）是用于解决非线性薛定谔方程的一种七点迭代格式，它可以更准确地模拟无线信号传输状况。

它有较低的运算量，可以获得较高精度的解。

多阶步函数差分格式（MSDF）是用于解决非线性薛定谔方程的一种变阶函数形式，它可以更准确地模拟信号的非线性传输过程，同时具有低的运行复杂性和高的计算精度，减小了计算时间。

总之，非线性薛定谔方程的不同差分格式均有不同的特征，决定了它们之间的特点和性能差异，旨在满足不同信号处理需求。

狄拉克函数的导数DiLorenzo函数（也称为Dilorenzo变换）是一种用于解决复杂、非线性多元方程组的有效解法。

它可以有效地减少多项式方程的维度，并对多项式进行高精度求解。

它是一种极具革命性的想法，并且在数学、物理和工程领域都有广泛的应用。

DiLorenzo函数的导数可能看起来很复杂，但关键是要理解这种函数的基本原理。

该函数的基本原理是将一个多项式分解成一组更简单的多项式，而每个更简单的多项式都可以作为一个新的变量进行求解。

因此，可以利用求导法则计算DiLorenzo函数向量对新变量的偏导，然后用求导结果和新变量代替原有的多项式计算DiLorenzo函数的导数。

DiLorenzo函数的偏导可以通过多项式的分解法求出，以下是该函数的偏导公式：dF(x) = ∑ i=1(N) dFi(x)*Mi(x)+ ∑ i=1(N) Fj(x)*Mj'(x)其中，dFi(x)表示DiLorenzo函数中第i个更简单的多项式的偏导，而Fj(x)、Mj(x)和Mj'(x)分别表示DiLorenzo函数中第j个更简单的多项式、第j个更简单的多项式的系数和第j个更简单的多项式关于x的导数。

DiLorenzo函数的偏导可以用来求解多元方程，极大地提高了求解的精度，减少了误差，提高了效率，因此在工程、物理、数学等各种领域都受到了广泛的应用。

总之，DiLorenzo函数是一种非常有用而有效的数学工具，它可以用于解决复杂的多项式方程组，具有非常高的求解效率。

它的导数的求解方法也可以应用于更多的问题，使用DiLorenzo函数可以明显提高求解的效率，给我们带来更加优质的应用结果。

dirac方程范文Dirac方程是物理学家Paul Dirac于1928年提出的一种描述电子的量子力学方程。

这个方程在量子力学中具有重要的地位，因为它是唯一一个既满足相对论性要求，又能描述自旋半整数粒子的方程。

Dirac方程的提出是基于两个重要的物理观察：电子具有自旋，且遵守相对论性的粒子动力学。

根据量子力学的标准操作，粒子可以用波函数来描述。

对于描述电子这种自旋1/2粒子的波函数，只需要包含两个分量即可。

但是，由于电子的自旋性质与相对论性质同时存在，波函数必须同时满足薛定谔方程和狄拉克方程。

狄拉克方程的形式为：(iℏγ^μ∂_μ-mc)Ψ=0其中，i是虚数单位，ℏ是普朗克常数除以2π，γ^μ是一组四个γ矩阵，∂_μ是四维导数算符，m是电子的静止质量，c是光速。

这个方程展示了相对论性的粒子动力学特征，其中动量和能量由相对论四动量算符P^μ=(E/c,p_x,p_y,p_z)确定。

此外，狄拉克方程也显示了电子的自旋与电子的运动有关。

狄拉克方程的解Ψ不再是传统意义上的波函数，而是一个四分量的具有矢量性质的对象，每个分量可以看作一个波函数。

Dirac方程的成功解释了电子的自旋和相对论性质，并在粒子物理学的发展中发挥了重要作用。

其解的形式给出了电子在电磁场中的运动方程，展示了电子在不同自旋态之间的跃迁，以及电磁场中的电子-正电子对的产生和湮灭。

此外，狄拉克方程也为物理学家提供了预言物理现象的新思路。

最著名的例子是Dirac方程预言了反粒子的存在，即正电子。

方程的解中存在一个负能量解，被认为对应一个正粒子的反粒子状态。

不久之后，正电子被实验证实，进一步证实了狄拉克方程的准确性。

总结起来，Dirac方程是描述电子的一种重要的量子力学方程。

它结合了自旋和相对论性质，成功解释了电子的性质和相互作用，给出了电子在电磁场中的运动方程，并预言了正电子的存在。

Dirac方程对于现代粒子物理学的发展具有重要的意义，是理解基本粒子行为的关键。